豎向成層介質中標量波傳播問題的高精度人工邊界條件

李會芳，趙 密，杜修力

(北京工業大學城市與工程安全減災教育部重點實驗室，北京 100124)

在地下結構抗震分析中，有限元法因其靈活高效的特點，被廣泛用于有限域模擬。為了更有效地反映截斷無限土體的輻射阻尼效應，需要引入人工邊界條件[1]。人工邊界的適用性和精度直接影響計算結果的精度，并通過影響計算區域的大小而影響計算效率。城市抗震防災和重大工程項目建設中經常遇到豎向成層介質以及不規則地形場地。在我國西南部山嶺地區中這種地形地質條件較為常見，如滇中引水工程中香爐山隧道穿越的含多條斷裂帶的復雜地形地質條件[2]。廈門市軌道交通2 號線跨海盾構隧道穿越了基巖、基巖強風化、基巖全風化等多個地層[3]。不均勻介質和不規則地形場地條件引起復雜的波動反射和透射，會造成與均勻半空間場地明顯不同的動力反應。復雜場地中結構動力反應研究表明，不均勻地質和不規則地形的存在會對場地和結構的動力反應產生顯著影響[4-8]，在地下結構抗震分析領域引起越來越多的關注。建立豎向成層介質中的高精度人工邊界條件具有研究和實際意義。國內外研究者已提出大量人工邊界條件[9]，其中包括：粘性邊界[10]、粘彈性邊界[11]、透射邊界[12]、無限元法[13-14]、邊界元法[15-16]、Engquist-Majda 邊界[17]、Higdon邊界[18]、Bayliss-Turkel 邊界[19]、Dirichlet-to-Neumann(DtN) 邊界[20-23]、一致邊界(薄層法)[24-26]、比例邊界有限元法[27]、吸收層法如完美匹配層法[28-29]等。以上人工邊界條件主要用于均勻介質的半空間或全空間場地以及底部固定的單層或水平成層場地。

近年來適用于水平成層半空間場地的人工邊界條件得到進一步發展。2009 年，蔣通和田治見宏[30]提出一致邊界結合粘性邊界來處理水平成層半空間介質的波傳播問題，粘性邊界中阻尼器的吸能效果對整體精度影響較大。2011 年，Lee 和Tassoulas[31]提出一致邊界結合連分式吸收層的方法；2012 年，Jo?o 等[32]提出采用一致邊界結合完美匹配離散層來解決水平成層半空間介質的波傳播問題，分析表明連分式吸收層可等效轉化為完美匹配離散層，其中匹配層厚度為基于頻率和外行波入射角的純虛數。2015 年，Hamdan 等[33]提出采用一致邊界結合旁軸邊界來模擬水平成層半空間介質中波傳播問題，旁軸邊界采用二階泰勒展開代替半空間的解析剛度精度較低。2020 年，李會芳等[34]提出H 形高精度人工邊界處理水平成層半空間標量波傳播問題，此邊界應用簡單方便且能得到高精度、高效率的求解。

基于水平成層半空間場地中人工邊界條件的研究工作，本文針對含豎向成層介質以及不規則地形場地中標量波傳播問題，建立了頻域下折線形高精度人工邊界條件。豎向成層介質的底邊界采用廣義一致邊界來擬合，通過適當的空間變換并精確模擬兩側的半空間剛度，將原來適用于表面自由、底部固定的一致邊界擴展應用于兩側開放的豎向成層介質底邊界；成層介質側邊界采用基于連分式的高精度邊界。由于提出邊界的高精度特性，有限域可以取得盡量小，對于無內域結構僅關心地表反應的情況，可以直接將人工邊界加在地表，極大地減少自由度，提高計算效率。通過在每個豎層邊界上引入斜角變換，廣義一致邊界可以為任意折線形，適用于豎向成層、不規則地表的場地反應。

1 問題描述

地震作用下重大基礎設施結構的動力響應需考慮與周圍介質的相互作用，形成無限域介質中的波傳播問題。圖1(a)所示為二維豎向成層半空間場地中的標量波傳播問題，場地中包含任意不規則地形以及廣義結構。為高效求解出平面波動問題，引入人工邊界分別將豎向地層和兩側無限域截斷，如圖1(b)所示計算模型1 由人工邊界條件與內域有限元部分組成，其中有限域中可以包含任意不均勻、非線性材料以及不規則結構，采用有限元法模擬。由于提出人工邊界條件的高精度，有限域尺寸可以盡量小。對于不含地下結構僅關心地面反應的情況如圖1(c)所示，可以直接將人工邊界加在地表，僅用折線形高精度人工邊界條件來模擬豎向成層半空間場地，如圖1(d)中計算模型2，最大限度減少計算自由度高效求解地表反應。

圖1 豎向成層且地表起伏的半空間場地中標量波傳播問題Fig. 1 Scalar wave propagation in half space including vertical stratified media and irregular topography

半空間場地中，左右兩側無限域以及豎向無限延伸的地層內為均勻線彈性材料。頻域下標量波傳播問題的控制方程為：

地表為自由邊界條件，各豎向地層和無限域之間的交界面以及人工邊界兩側均滿足位移和應力連續條件。另外，滿足無限遠處輻射條件以及初始靜止條件。

2 高精度人工邊界條件

以圖1(b)中計算模型1 為例給出本文高精度折線形人工邊界條件的實現過程。不含廣義結構時，人工邊界條件可加在地表處，此時計算模型中無內域和豎層側邊界，計算模型1 簡化為圖1(d)中計算模型2。另外，計算模型1 中豎層底邊界可以根據結構形式、計算效率等需要設置為任意角度折線形邊界。

2.1 兩側無限域連分式邊界

則側邊無限域y方向的動力剛度為：

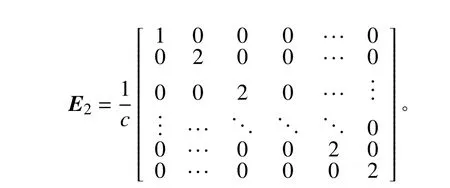
以上為左側無限域的人工邊界條件，同理可以得到右側無限域的人工邊界條件。

2.2 豎層底部廣義一致邊界

2.3 有限域與人工邊界條件耦合

將有限域側邊力位移關系的連分式展開式(11)沿豎向x軸離散，通過線性插值得到側邊人工邊界條件有限元方程：

將有限域與底部人工邊界條件式(17)以及兩側人工邊界條件式(18)組裝，得到頻域下耦合系統有限元方程：

式中，下標I、B、C分別對應內域自由度、邊界自由度以及連分式引入的輔助自由度。

3 數值算例

本節給出不同地形、地質條件下四種場地中波傳播問題的數值算例來驗證提出高精度折線形人工邊界條件的有效性和精度。參考解為大區域有限元模型的時域解，模型尺寸足夠大能夠保證在觀測時間內結果不受到截斷邊界處反射波的影響。同時采用了簡單常用的粘彈性人工邊界條件[11]進行了對比分析，說明提出的折線形人工邊界條件適用于豎向成層不規則地形場地，且在計算精度上有顯著改進。本文人工邊界條件中連分式階數統一取為5 階，階數為零時可退化為旁軸近似。采用Ricker 波作為荷載，其時程和頻譜曲線如圖2 所示。

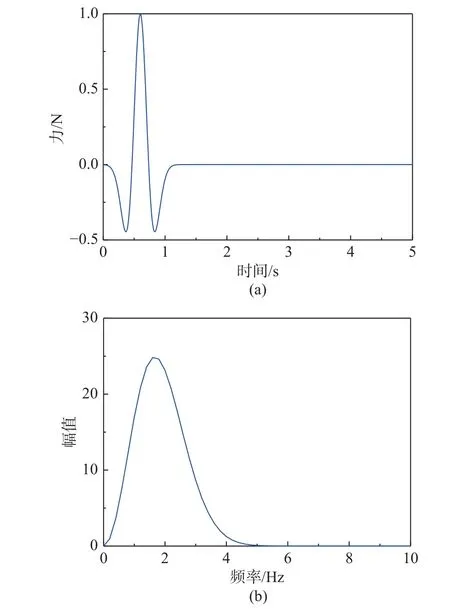
圖2 Ricker 波的時程和頻譜曲線Fig. 2 Time history and Fourier spectrum of Ricker wavelet impulse

3.1 水平地表場地

平直地表半空間場地中含有一個豎向無限延伸地層，如圖3 所示。中間地層的剪切波速c1=100 m/s，兩側無限域介質剪切波速c2= 200 m/s。坐標原點取地表中心點A。計算中選取了兩種形式的人工邊界，如圖3 中點劃線和虛線所示。加載點為點A，觀察點為A(0, 0)、B(0, -100)、C(100, 0)、D(100, -100)。有限元網格尺寸為2 m，計算時間步長為0.01 s。

圖3 含豎直地層半空間場地中標量波傳播問題Fig. 3 Scalar wave propagation in half space field with one vertical layer

觀察點的位移時程結果如圖4 所示。將采用新邊界的兩種計算模型和采用粘彈性邊界的計算模型1 與采用大區域有限元模型得到的參考解進行比較。其中計算模型1 由人工邊界條件與內域有限元部分組成，如圖3 中點劃線所示區域；計算模型2 為直接將人工邊界加在地表，如圖3 中虛線所示。下文中圖例意義相同。從圖中可以看出，無論是加載點還是邊界處節點以及材料交界面上節點，采用新人工邊界條件的兩種模型計算結果均與參考解吻合較好，而粘彈性邊界模型在邊界及材料交界面節點上計算誤差較大。驗證了新提出人工邊界條件的有效性和精度。

圖4 水平地表場地中觀察點位移時程結果Fig. 4 Time histories of displacement solutions at observation points in a flat surface site

3.2 折線地表場地

折線形地表半空間場地中含有兩個豎向地層，如圖5 所示。左側地層的剪切波速c1=100 m/s，右側地層的剪切波速c2= 300 m/s，兩側無限域介質剪切波速c3= 200 m/s。圖5 中各點坐標為A(0, 0)、B(50, 50)、C(150, 0)、D(0, -50)、E(50, -50)、F(50,-50)，其中加載點為B，觀察點為B、C、E、F。有限元網格尺寸為1 m～3 m，計算時間步長為0.002 s。

圖5 含豎向成層介質且地表起伏的半空間場地中標量波傳播問題Fig. 5 Scalar wave propagation in half space field with vertical stratified media and irregular topography

觀察點的位移時程結果如圖6 所示。觀察點包括地表節點、人工邊界上的節點以及材料交界面處的節點。從圖6 中可以看出，兩種新邊界計算模型的位移解與參考解吻合較好，而粘彈性邊界模型在邊界及材料交界面節點上計算誤差較大。表明提出的人工邊界條件可以很好的模擬邊界處和材料變化帶來的反射和散射波，以及隨時間空間變化的輻射效應，驗證了新人工邊界條件的有效性和精度。

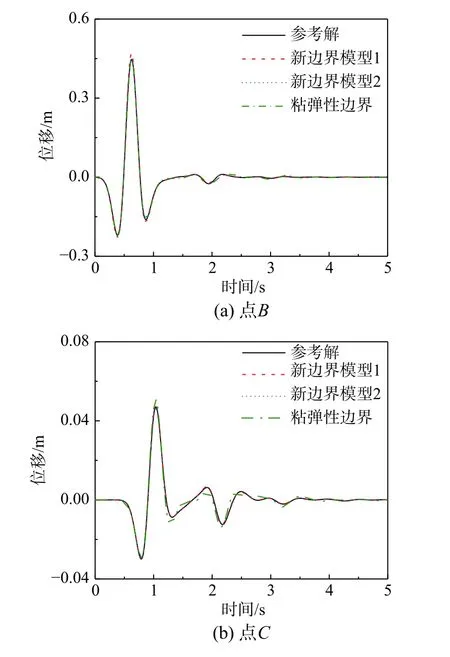
圖6 折線地表場地中觀察點位移時程結果Fig. 6 Time histories of displacement solutions at observation points in a zigzag terrain site

3.3 階梯地形場地

階梯地形半空間場地中含有三個豎向地層，如圖7 所示。從左到右介質剛度依次增大，左側無限域介質剪切波速cl= 100 m/s，三個豎向地層的剪切波速分別為c2= 150 m/s、c3= 200 m/s、c4=250 m/s，右側無限域介質剪切波速c5= 300 m/s。圖7 中定位點坐標為A(0, 0)、B(50, 50/3)、C(100,100/3)、D(150, 50)、E(0, -50)、F(50, -50)、G(100,-50)、H(150,-50)，其中加載點為B，觀察點為A、C、E、G。有限元網格尺寸為1 m～2.2 m，計算時間步長為0.002 s。

圖7 含豎向成層介質的階梯地形半空間場地中標量波傳播問題Fig. 7 Scalar wave propagation in step-shaped half space field with vertical stratified media

觀察點的位移時程結果如圖8 所示。觀察點包括地表節點、人工邊界上的節點以及材料交界面處的節點。從圖8 中可以看出，兩種新邊界計算模型的位移解與參考解吻合較好，而粘彈性邊界模型在邊界及材料交界面節點上計算誤差較大。表明新人工邊界條件可以很好的吸收邊界以及材料變化產生的反射和散射波，模擬無限場地的輻射效應，驗證了新人工邊界條件的有效性和精度。

圖8 階梯地形場地中觀察點位移時程結果Fig. 8 Time histories of displacement solutions at observation points in a stepped terrain site

3.4 含地下結構場地

如圖9 所示，地下結構建立在含豎向成層介質且兩側不等高地形的半空間場地中，其地表高低起伏可模擬河谷與山坡同時存在的復雜地形，本算例分析其中的標量波傳播問題。從左到右5 種介質剛度依次增大，左側無限域介質剪切波速cl= 100 m/s，三個豎向層的剪切波速分別為c2=150 m/s，c3= 200 m/s，c4= 250 m/s，右側無限域介質剪切波速c5= 300 m/s。因含有地下結構，計算模型2 不再適用或者說誤差較大，本節僅采用計算模型1 與參考解比較，人工邊界位置如圖9中點劃線所示，分別施加新邊界條件和粘彈性邊界條件[11]。圖9 中定位點坐標為A(0, 0)、B(50, -20)、C(150, 30)、D(200, 10)、E(0, -50)、F(50, -50)、G(150, -50)、H(200, -50)，地下結構圓心坐標為(100, -30)，半徑10 m。其中加載點為B，觀察點為B、C、E、H以及地下結構上節點C1(90, -30)、C2(100, -20)。有限元網格最大尺寸小于4 m，計算時間步長為0.002 s。

圖9 含地下結構的復雜地形地質半空間場地中標量波傳播問題Fig. 9 Scalar wave propagation in complex topographical geological half space field including an underground structure

觀察點的位移時程結果如圖10 所示。觀察點包括地表節點、人工邊界和材料界面處的節點以及地下結構上的節點。從圖10 中可以看出，新人工邊界條件可以很好地模擬邊界處、材料界面以及地下結構帶來的反射波和散射波，以及隨時間空間變化的輻射效應。新邊界計算模型的場地反應和結構反應均與參考解吻合較好，而粘彈性人工邊界誤差較大。驗證了新人工邊界條件的有效性和精度。

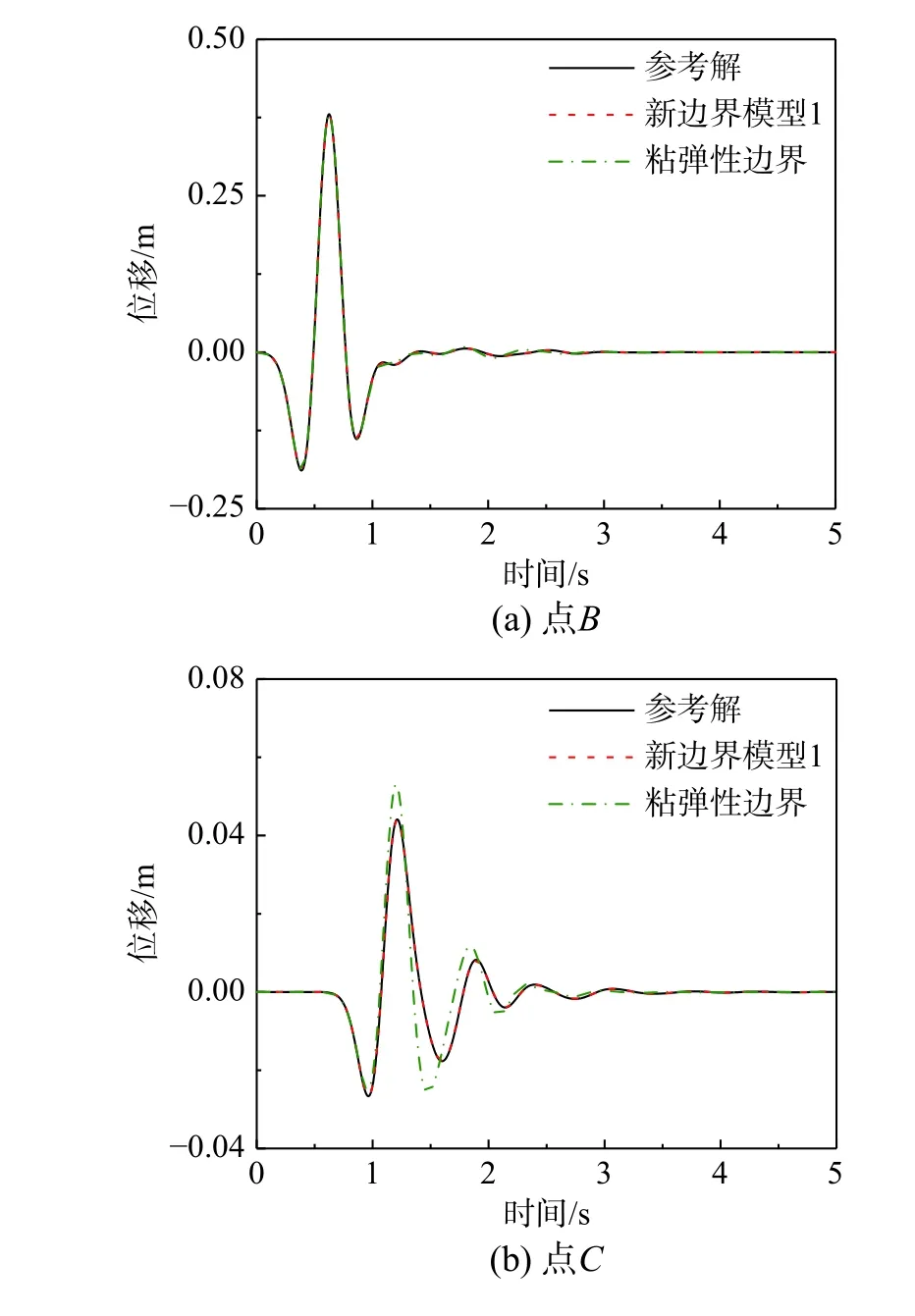
圖10 含地下結構場地中觀察點位移時程結果Fig. 10 Time histories of displacement solutions at observation points in a site containing underground structure

4 結論

本文針對豎向成層介質中的標量波傳播問題，基于連分式展開和擴展的一致邊界，建立了含豎向成層介質和地表不規則場地的折線形高精度人工邊界條件。半空間場地劃分為豎向成層介質以及兩側無限域。兩側無限域的人工邊界條件基于動力剛度的連分式展開，引入輔助變量來模擬無限域輻射效應；豎向成層介質為廣義的一致邊界，兩端開放與側邊連分式邊界耦合，并引入斜角變換使得提出的人工邊界條件可以為任意折線形。側邊界與底邊界耦合后的折線形人工邊界可用于豎向成層介質中標量波傳播分析。數值算例結果表明，提出的高精度人工邊界條件適用于多種豎向成層介質中標量波傳播問題，具有較高的計算精度，極大提高計算效率。

與水平成層半空間中標量波傳播問題的H 形人工邊界[34]相比，本文折線形人工邊界條件主要是對原有方法的擴展應用。水平成層半空間模型轉換到豎向成層半空間模型的過程中，多層和半空間區域的無限延伸方向以及物理邊界均發生變化，人工邊界的截斷位置也隨之改變。因此針對水平成層半空間中的人工邊界條件不再直接適用，但具有重要參考價值。為進一步擴展人工邊界條件的適用范圍，適用于傾斜地層的人工邊界條件正在研究中。