豎向荷載作用下飄浮體系斜拉橋極限承載能力與失效模式分析

呂文高，何 政

(1. 貴州民族大學建筑工程學院，貴州，貴陽 550025；2. 大連理工大學土木工程學院，遼寧，大連 116024)

大跨斜拉橋以其卓越的跨越能力、優美的外觀造型等特點在我國得到廣泛的應用[1-2]，進而成為國家重大基礎設施(如高速公路及鐵路等)的關鍵節點。近年來，全球范圍內極端災害頻發，嚴重威脅處于重要交通樞紐位置上的大跨斜拉橋的運營，關于大跨度斜拉橋損傷與失效機制的基礎研究已成為我國經濟社會發展的迫切需求。極端作用下的結構往往出現諸如塑性變形、漸進破壞、整體失穩，直至倒塌等大變形、大位移過程。斜拉橋結構的大位移和局部大應變是結構失效破壞的重要原因之一，其性態往往表現為較強的幾何非線性和材料非線性效應。目前尚缺少成熟有效的分析理論和方法，因此，開展大跨度斜拉橋的塑性失效機理研究是非常必要的，同時也是亟待解決的關鍵問題。

目前，結構的損傷倒塌機理研究主要集中在建筑結構領域[3-4]，橋梁結構特別是斜拉橋的損傷失效機制研究卻相對較少。同時，橋梁結構質量主要沿橋跨分布導致其可能的倒塌機制與建筑結構是不同的[5]。結構的損傷倒塌分析方法主要包括有限元法和塑性極限分析法。首先，有限元法方面主要是通過彈塑性分析得到斜拉橋的倒塌荷載[6-7]及其構件的損傷失效情況。然而，有限元法要不斷的生成整體剛度矩陣并通過迭代求解非線性方程組[8]來獲得結構的響應，求解費事費力[9]且收斂性問題也比較突出。在拱橋破壞的有限元分析方面，黃盛楠等[10]采用MSC.Marc 有限元軟件進行了因超載導致的鋼筋混凝土連續倒塌過程分析，并用構件重要性評價方法驗證分析結果的準確性；彭衛兵等[11]基于OpenSEES 平臺的實體單元建模進行了圬工拱橋的內力分析和漸進式倒塌過程模擬，結果表明：兩者的預測結果一致。在斜拉橋損傷破壞的有限元分析方面，林楷奇等[12]結合OpenSEES 和MSC.Marc 有限元軟件建立了主跨1500 m 的特大跨斜拉橋有限元模型，進而實現了地震災變及倒塌全過程的模擬，驗證了開發的計算單元和模型的可行性與正確性；宗周紅等[13-14]通過LS-DYNA 有限元軟件建立了大跨度斜拉橋顯式積分有限元模型，探究強震作用下大跨度斜拉橋的倒塌破壞模式。其次，塑性極限分析法方面則是基于極限分析的運動學原理研究斜拉橋的失效荷載及破壞模式。該方法由Kazinczy[15]在研究梁的極限載荷時提出，可直接建立結構的塑性極限狀態與極限載荷之間的關系，無需結構整體剛度矩陣及完整的載荷歷史，并結合優化方法獲得結構的極限承載力與相應的失效模式。Jirásek 和Bazant[16]通過其專著對塑性極限分析法在各建筑結構中的應用進行了系統、全面的梳理與總結，為該方法在其他類型結構中的應用提供了便利。目前，塑性極限分析法主要用于框架結構[17-18]、梁和柱[19]及砌體石拱橋結構[20-23]的極限承載力計算中，如Brandonisio 等[24]結合該方法和試驗分析研究了砌體門式平面框架的水平抗震能力，可揭示結構倒塌破壞的基本行為，是簡單快速評估結構抗倒塌能力的一種方法。Brandonisio等[25]通過該方法評估了砌體圓形支承拱的倒塌荷載和塑性鉸位置，證明是一個簡單可靠的初步分析工具且數值實現容易。Da 等[26]基于該方法計算了誘發單跨及多跨鐵路石拱橋產生縱向和橫向倒塌的極限水平加速度，表明塑性極限分析法可用于石拱橋的地震安全初步評估和橋梁的維護管理。近年來，結合各種優化方法的塑性極限分析法被應用于較為復雜框架結構的承載力及倒塌機制分析中[18,27-29]，這進一步擴展了該方法的應用范圍。然而，塑性極限分析法在橋梁結構特別是斜拉橋結構中應用很少，僅Yan 等[30-31]提出采用該方法研究了支承體系斜拉橋的倒塌荷載，并在此基礎上分析其易損性，但文中未詳細闡述或證明該方法在斜拉橋結構中的適用性，也未對飄浮體系、控制體系斜拉橋等做進一步研究。拉索銹蝕是斜拉橋運營中的主要危害之一，有些剛建成不久就換索(如德國漢堡的Kohlbrand Estuary 橋)；有些則因銹蝕斷索事故造成了嚴重的社會影響，且花費了巨資更換拉索(如廣州海印大橋)。因此，對于運營中的斜拉橋而言，拉索銹蝕作為突出的問題，是結構性能退化及影響安全服役的重要因素。嚴重的拉索銹蝕不僅影響其本身的極限強度、伸長率及疲勞強度[32]，還會明顯改變斜拉橋結構的整體剛度、變形及承載力[33]，甚至改變失效模式[34-36]、增加結構的失效風險。由于拉索銹蝕的局部性，目前除了有限元法外，還未有其他有效分析方法能考慮拉索銹蝕對整個斜拉橋結構失效行為的影響。綜上所述，塑性極限分析法在大跨斜拉橋結構失效機理的研究中還未得到廣泛應用。

結合塑性極限分析方法的原理與優點，本文在文獻[30]研究的基礎上嘗試將其應用于豎向荷載作用下漂浮體系斜拉橋的極限承載力和失效模式的研究中，進而分析部分拉索銹蝕對整個斜拉橋結構失效行為的影響，完善服役斜拉橋安全評估的理論與方法，為斜拉橋結構的初步設計及其控制措施制定提供重要參考。主要研究內容如下：① 計算斜拉橋極限承載力(塑性倒塌荷載)；② 識別斜拉橋的失效模式；③ 分析構件損傷(如拉索和主梁)與倒塌載荷及失效模式之間的關聯性；④ 分析拉索銹蝕對斜拉橋極限承載力及失效模式的影響。

1 斜拉橋塑性極限分析理論

1.1 基本假定

研究所采用假定如下：① 材料采用理想剛塑性模型；② 采用小變形假定，因此變形前后的平衡方程都參照初始構型構建，應變-位移之間的幾何關系是線性的；③ 由于拉索對主梁的足夠支承，因此可假定密索體系斜拉橋在達到極限荷載以前不會出現屈曲失效；④ 假定結構倒塌為穩態過程，可不考慮慣性效應；⑤ 外荷載同比例增加，符合簡單加載條件；⑥ 假定基本破壞機構范圍內所包含的全部拉索都達到屈服。

1.2 塑性倒塌荷載定義

設軸向屈服構件的屈服內力為F，彎曲屈服構件的塑性彎矩為M，則所有屈服構件的塑性耗散功率為[37]：

1.3 斜拉橋破壞機構

若結構為r次超靜定結構，且由于塑性極限分析中極限載荷系數λ 也是待定的，因此，在斜拉橋結構倒塌瞬時共有r+1 個多余未知量。根據結構力學知識可知，r次超靜定結構要想變成破壞機構，至少需要r+1 個截面或構件屈服才能使其成為有1 個自由度的機構。因此，若要唯一確定結構破壞時的內力，必須在靜力平衡方程之外，再增加r+1 個條件。r+1 個構件或截面屈服時的內力值已知，這等于在靜力平衡方程之外增加了r+1 個已知條件，此時，結構倒塌破壞時所有的內力和載荷參數都可以完全確定，因此，其破壞機構為完全破壞機構。若在斜拉橋結構內部屈服構件或截面數少于r+1，此時雖然不會產生完全破壞機構，但也能使結構局部成為破壞機構，為不完全破壞機構。對于不完全破壞機構，其載荷系數及內力是唯一確定的，但未變成機構的部分則是不能唯一確定的。由于，塑性極限分析過程中不可能要求結構的全部內力都能唯一確定，因此，完全破壞機構和不完全破壞機構都是允許的。對于斜拉橋破壞機構而言，r+1 個截面屈服包括屈服拉索和主梁的若干個塑性鉸。由于結構的破壞機構往往有很多個，不可能全部進行分析，為此，只需要找出基本機構并通過其組合成為能包含所有破壞機構的情況即可。具體證明如下[38]：

由于結構的各基本機構是線性獨立的，因此任何破壞機構都可由基本機構組合而成。設結構最終的失效機構場與各基本機構之間的幾何關系可表示為：

式中：Fyi為第i個屈服構件的軸力；Mpi為彎曲屈

式(12)表明結構最終的破壞機構可由各基本破壞機構的線性疊加而成，這正是本文基于塑性極限分析法研究斜拉橋豎向荷載作用下極限承載力和失效模式的依據。同時，根據式(8)和式(12)可得，對于任意一個可能破壞機構相應的Fyi和Mpi，滿足式(12)的破壞機構必為真實的破壞機構。一般對于具體的結構和荷載而言，其獨立的基本破壞機構往往是較少且易識別的。上述證明可得，斜拉橋的破壞機構都可由基本破壞機構組合疊加而成，因此，在斜拉橋具體的失效機理分析過程中，首先，可基于基本破壞機構組合表示出倒塌破壞機構，然后，依據最小能量原理并借助優化方法識別出最小倒塌載荷系數λu及其對應的失效模式，即為斜拉橋結構真實的極限承載力及倒塌失效模式。

首先，飄浮體系斜拉橋的恒載及車輛荷載主要通過拉索傳遞給索塔，因此，相比于支承體系，飄浮體系斜拉橋拉索受力更為不利；其次，飄浮體系斜拉橋拉索長期處于較高應力狀態下，導致其在惡劣環境中更易腐蝕受損；再者，相比于支承體系，飄浮體系的超靜定次數相對較低，冗余度較低，極端荷載作用下發生破壞的風險較大；最后，跨徑大、密索體系或在地震地區修建的斜拉橋一般可選飄浮體系斜拉橋。為此，本文關于斜拉橋結構失效機理的探討主要集中于飄浮體系。

飄浮體系斜拉橋的上部結構主要由斜拉索、主梁及索塔組成，斜拉索將索塔和主梁連接起來，索塔和主梁之間未直接有連接構件，可認為索塔和主梁是相對獨立的構件。由于拉索的柔性支承作用，主梁相當于多跨連續梁，索塔相當于懸臂梁，主梁-拉索和索塔-拉索可分別形成各自的破壞機構，即為斜拉橋的基本破壞機構，也可稱為梁-拉索型破壞機構。斜拉橋的橋墩與主梁之間通常為滑動鉸支座連接，在考慮橋墩的情況下，豎向荷載作用下塑性鉸仍然集中于主梁上，因此，可通過墩-梁-拉索型基本機構考慮橋墩對極限承載力和失效模式的影響。框架結構的基本破壞機構主要包括三種，分別為梁型基本機構、層間側移型基本機構和節點型基本機構(如圖1 所示)。為此，類比框架結構并結合基本假定，可認為飄浮體系斜拉橋在豎向荷載作用下的基本破壞機構主要包括簡支梁-拉索型基本機構、懸臂梁-拉索型基本機構和墩-梁-拉索型基本機構(如圖2 所示)，斜拉橋所有的破壞機構都可以通過上述基本機構的組合疊加而成[39-40]。

圖1 框架結構的基本機構[39]Fig. 1 Typical elementary mechanisms of frame structures[39]

圖2 斜拉橋梁-拉索型基本機構Fig. 2 Elementary mechanisms of cable-stayed bridges with floating systems

1.4 斜拉橋塑性倒塌荷載

根據斜拉橋結構的受力特點(如圖3 所示)，索塔只要出現1 個塑性鉸就可形成不完全破壞機構，而主梁則需要多個塑性鉸才能形成破壞機構。

圖3 斜拉橋荷載傳遞特點Fig. 3 Load transfer characteristics of cable-stayed bridges

圖4 表明飄浮體系斜拉橋索塔處主梁截面為最大軸力處，且有一定的彎矩，因此，根據壓彎構件的N-M破壞曲線可知，該處截面最易因小偏心受壓破壞而形成塑性鉸。然而，主梁若要形成不完全破壞機構，需至少形成3 個塑性鉸。盡管索塔根部截面的軸力及彎矩等內力都比較大，但由于截面尺寸較大，因此，其塑性鉸不一定出現在根部。索塔上部由于兩側拉索的支承作用，塑性鉸一般也不會出現在此位置。由此可知，單塔飄浮體系斜拉橋(不考慮橋墩影響)的塑性鉸位置可假定為：索塔處主梁截面、左跨度內某處及右跨度內某處，索塔的塑性鉸位于索塔最內側拉索與索塔根部之間某處。根據前面關于塑性鉸位置和基本破壞機構的描述，單塔飄浮體系斜拉橋的組合破壞機構(這里未考慮橋墩的影響)如圖5 所示，需要注意的是各基本破壞機構內的拉索全部為屈服狀態。由于，斜拉索為僅受拉構件，為此，在計算屈服構件的塑性耗能功率時，拉索的軸向虛位移率必為正值，此條件在優化計算結構倒塌荷載及識別倒塌模式時轉變為目標函數的約束條件。具體描述如下：

圖4 斜拉橋主梁軸力分布(Ng(x)為主梁x 處軸力，Ng, max 為主梁最大軸力)Fig. 4 Distribution of axial force of girder in cable-stayed bridges (Ng(x) is axial force of girder with position x and Ng, max is the maximum axial force of girder)

圖5 飄浮體系單塔斜拉橋倒塌失效機構Fig. 5 Collapse mechanism of cable-stayed bridges with floating systems

1)塑性耗散功率

根據假定，斜拉橋塑性倒塌時塑性耗散功率可表示為：

因此有：

4)基于線性規劃的失效模式優化識別

單純形法是線性規劃中應用最廣泛的經典優化方法，但隨著目標問題約束條件的增加，該方法的迭代次數也迅速增加，甚至導致收斂困難，于是新的優化方法-內點法開始被廣泛應用。內點法的基本思想是從可行域內部的一個初始點(如圖6的x0點)出發，沿著能使目標函數下降最快的方向找到新內點(如圖6 的x1點)，再從這個新內點出發，沿著可行方向不斷迭代求出后續內點，直至獲得最優解如(如圖6 所示)。相比較而言，單純形法需要搜尋大部分甚至所有可行域的頂點才能收斂(如圖6 所示)，而內點法是在可行域內部尋優，迭代次數因約束條件的增加而變化的比較少，其計算速度和收斂性均優于單純形法，且對問題規模不敏感，適用于大系統的優化。因此，對于大規模優化問題，內點法要優于單純形法。

圖6 單純形法與內點法尋優路徑[41]Fig. 6 Optimization path of simplex method and interior point method[41]

內點法基本原理如下：內點法是從可行域內部的某個可行點出發，不斷迭代尋找最優解。優化過程中，新內點要始終在可行域內，為防止其越過邊界，可在約束邊界內設置障礙，即構造罰函數(當新內點遠離邊界時，懲罰值很小的，反之則迅速增大懲罰值)。約束邊界設置障礙尤如在邊界上修筑了一道墻根圓滑的高墻，使新內點始終落在可行域內，故將該方法稱為“內點法”或“障礙法”。根據其基本原理[42-43]及本文研究的具體問題，目標函數及約束條件表示如下：

上述優化問題可利用內點法(interior point method)求解，首先構造罰函數形式為：

由式(18)～式(19)可知，斜拉橋結構的極限載荷計算和失效模式識別包含兩組參數：其一是破壞機構場中拉索、主梁及索塔塑性鉸的各虛位移率參數，如e˙ci、 θ˙g1、 θ˙g2、 θ˙g3及 θ˙t；其二是主梁和索塔的塑性鉸位置參數，如l1、l2、h1或h2，兩組參數同時優化很困難。為此，本文結合內點法并采用MATLAB 編程進行優化，具體步驟為：① 在給定的塑性鉸位置參數下得到基于該位置參數的最優解；② 改變位置參數繼續計算，得到多個極限載荷系數λ[44]；③ 所有載荷系數λ 的最小值λu為同時符合兩組機構場參數的最優解-斜拉橋結構真實的倒塌載荷，同時與λu對應的各位置參數及各虛位移率參數所表征的失效機構即為結構的真實倒塌失效模式。

2 算例分析

本文以某大跨度飄浮體系單塔斜拉橋為例，討論采用塑性極限分析法研究其失效行為的準確性與可行性，并據此分析拉索銹蝕對豎向荷載作用下斜拉橋結構極限承載力和失效模式的影響。

2.1 斜拉橋概述

如圖7 所示，某飄浮體系斜拉橋跨度為600 m，左右跨均為300 m，索塔高175.5 m，拉索沿橋跨對稱且等間距布置，主梁與索塔之間無直接連接。主梁左端為鉸接約束，右端為滑動支座約束。結構材料參數設置為：① 主梁：彈性模量為210 GPa，剪切模量為80 GPa，泊松比為0.3，截面面積為1.0175 m2，塑性模量為1.1462 m4及屈服強度為340 MPa；② 拉索：彈性模量為200 GPa，泊松比為0.3 及屈服強度為1500 MPa；③ 索塔：彈性模量為33 GPa，剪切模量為14 GPa，屈服強度為60 MPa，泊松比為0.15，各段截面面積及慣性矩如圖7 所示；④ 豎向恒、活荷載均布于主梁上，為190 kN/m[44]。由于本文的主要目的是驗證方法在飄浮體系斜拉橋中的適用性，因此參數分析中單根拉索銹蝕考慮為均勻銹蝕，銹蝕率采用假定值。算例中的拉索強度系數為以實際斜拉橋設計時的拉索屈服強度fcy0為參考值對塑性極限分析過程中所采用的屈服強度fcy進行放大或縮小的比例系數，即拉索強度系數=fcy/fcy0。主梁強度系數的定義與拉索強度系數的定義類似，即主梁強度系數=fgy/fgy0，其中fgy0為實際斜拉橋設計時的主梁屈服強度。后續章節中拉索強度與主梁強度之比是指當主梁強度不變，拉索強度發生變化時，兩者的相對比值；主梁強度與拉索強度之比是指當拉索強度不變，主梁強度發生變化時，兩者的相對比值。

圖7 飄浮體系單塔斜拉橋模型概況 /mFig. 7 Introduction of single tower cable-stayed bridge with floating system

為驗證方法的準確性與可行性，本文基于OpenSEES(open system for earthquake engineering simulation)平臺建立斜拉橋二維結構分析模型。該平臺綜合了截面分析、靜力彈塑性分析、動力分析等多種功能，能較好模擬荷載作用下結構的非線性響應。為了更好模擬主梁的塑性鉸行為，本文在有限元模型中將零長度單元(Zero-Length Element)加入各主梁單元節點之間(如圖8 所示)。零長度單元的水平方向和豎向自由度均通過耦合(EqualDOF)實現，彎曲自由度采用彈簧模擬，其轉動剛度等于主梁的初始轉動剛度。當形成塑性鉸時，零長度單元的轉動剛度為零。索塔的強度和剛度都比較大，一般不產生塑性鉸，因此，在有限元分析時索塔采用彈性梁-柱單元。主梁采用彈塑性梁-柱單元，拉索采用桁架單元，主梁及拉索材料均為理想彈塑性模型。采用非線性靜力Push-Down 分析，豎向荷載按比例增加，當計算出現因剛度矩陣奇異不收斂或變形發散時，對應的載荷即為其極限承載力[45]，對應極限荷載系數為λu，失效前的瞬時狀態即為倒塌或失效模式。

圖8 主梁單元節點間的零長度單元Fig. 8 Zero-Length Element in girder connection

2.2 結果分析與驗證

本文首先結合塑性極限分析方法研究斜拉橋拉索強度及主梁強度的變化對其失效行為的影響，并以此驗證該分析方法用于豎向荷載作用下飄浮體系斜拉橋失效分析的可行性和準確性。圖9(a)給出了飄浮體系單塔斜拉橋極限載荷系數λu與其失效模式隨拉索強度的變化規律。從圖中可得，飄浮體系單塔斜拉橋的極限載荷系數λu隨著拉索強度的增加而增加，但其非線性并不十分明顯。當拉索強度系數小于0.705，即拉索強度與主梁強度之比相對較小時，斜拉橋主梁呈現出整體性破壞特點，類似于豎向荷載下簡支梁的破壞形式，此時主梁塑性鉸僅有一個，且位于索塔處主梁截面，索塔未出現塑性鉸；當拉索強度系數大于0.705，即拉索強度與主梁強度之比相對較大時，斜拉橋主梁呈現出局部性破壞特點，此時主梁塑性鉸有三個，分別位于索塔處、左跨度L1位置處和右跨度L2位置處，同樣索塔未出現塑性鉸。圖9(b)給出了飄浮體系單塔斜拉橋的極限載荷系數λu與其失效模式隨主梁強度的變化規律。從圖中可得，飄浮體系單塔斜拉橋的極限載荷系數λu隨主梁強度的增加而增加，且非線性顯著。當主梁強度系數小于1.418，即主梁強度與拉索強度之比相對較小時，斜拉橋主梁呈現出局部性破壞特點，此時主梁塑性鉸有三個，分別位于索塔處、左跨度L1位置處和右跨度L2位置處，索塔未出現塑性鉸；當主梁強度系數大于1.418，即主梁強度與拉索強度之比相對較大時，斜拉橋主梁呈現出整體性破壞特點，類似于豎向荷載下簡支梁的破壞形式，此時主梁塑性鉸僅有一個，且位于索塔處主梁截面，同樣索塔未出現塑性鉸。

由圖9 可得，隨著拉索或主梁強度的變化，極限載荷系數λu都呈現出光滑連續的變化，但塑性鉸位置L1或L2均呈現出臺階式變化，兩者之間明顯不同，這意味著不同的拉索或主梁強度可能對應于相同的失效模式，同時表明主梁的失效模式的改變是非連續的。但從整體來看，拉索強度或主梁強度的改變都明顯改變著飄浮體系斜拉橋的失效模式。另外，圖9 也表明極限載荷系數λu的改變要更敏感于拉索強度的變化。

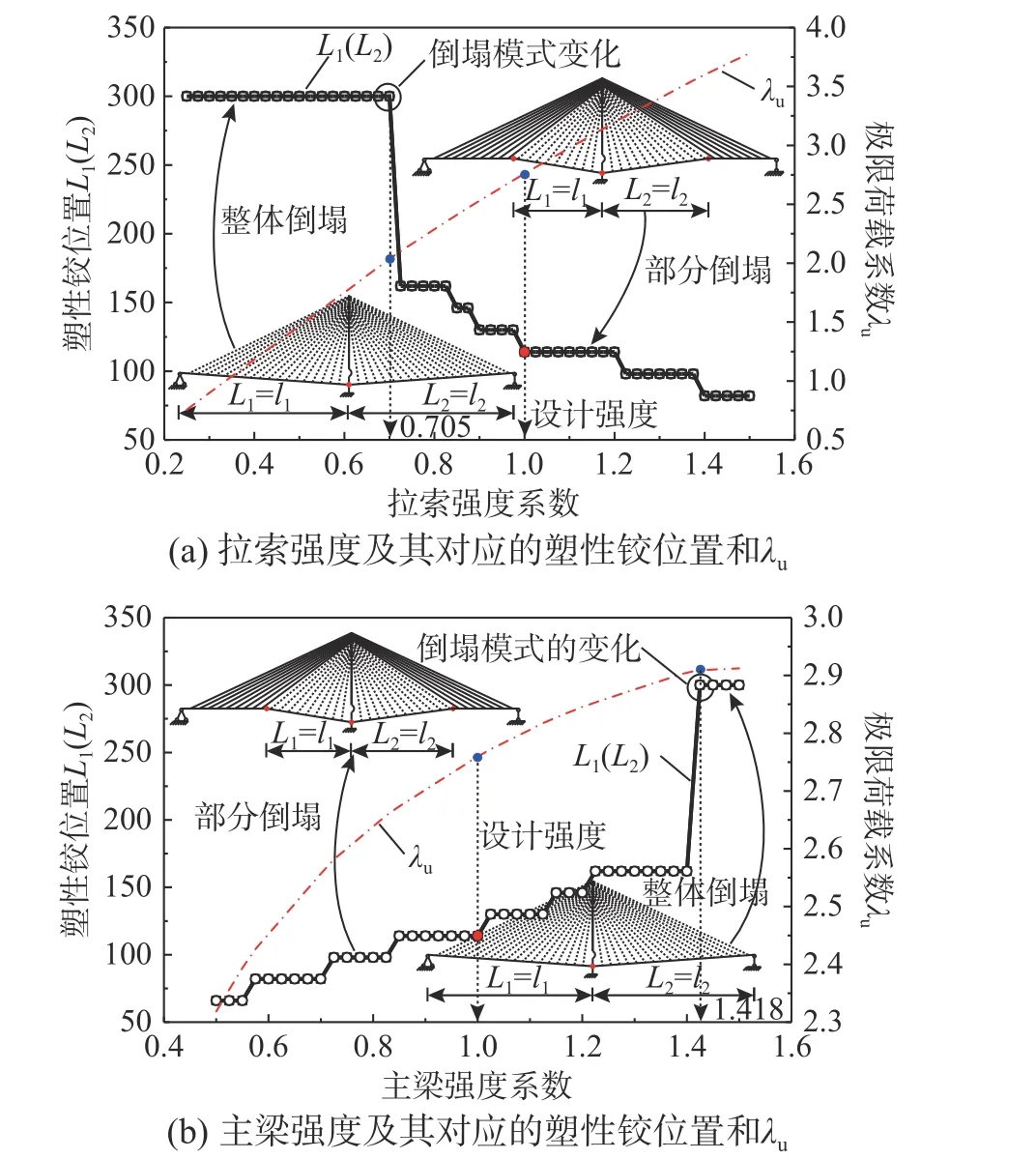
圖9 塑性倒塌機制隨拉索及主梁強度的變化(塑性極限分析法)Fig. 9 Variation of plastic collapse mechanism with cable and girder’s strength (plastic limit analysis method)

總結圖9 可得，隨著拉索強度的增加或主梁強度的減小，斜拉橋主梁失效呈現出由整體性轉變為局部性倒塌失效，這是失效模式類型的重要變化。其主要原因是：當拉索強度較低時，拉索對于主梁的約束限制作用也較小，進而導致主梁呈現出整體性破壞，反之則加強了對主梁的約束限制作用，導致主梁呈現出局部性破壞。根據圖9可得，促使斜拉橋失效模式類型改變的正是拉索強度與主梁強度之比，這正說明了斜拉橋失效機理不僅與拉索或主梁強度密切相關，還與兩者之比有重要關聯。上述分析結論對于斜拉橋的初步設計具有重要的指導意義。在實際的斜拉橋設計中，可通過塑性極限分析法得到拉索與強度之比的臨界值(如圖9 系數0.705 或1.418 對應的兩者的比值)，以此在提高斜拉橋抗倒塌能力的同時盡量避免不期望的失效模式的發生。

圖10 給出了塑性極限分析法與OpenSEES 計算結果的對比分析。由圖10(a)可知，隨著拉索強度的增加，OpenSEES 分析得到的極限載荷系數λu也不斷增加，兩者的誤差范圍為4.90%～20.78%，變化趨勢基本一致。同樣，由圖10(b)可知，隨著主梁強度的增加，OpenSEES 計算結果與塑性極限分析法得到的結果的變化趨勢也基本一致，兩者的誤差范圍為3.39%～12.45%。由于簡化分析方法是基于塑性極限分析理論中的上限定理得到的，因此，其計算結果通常偏高，這正是圖10 中塑性極限分析法得到的極限載荷系數高于OpenSEES所得結果的原因。圖10 表明：隨著拉索或主梁強度的增加，OpenSEES 計算結果與塑性極限分析法計算結果之間的誤差有增加的趨勢，特別是圖10(a)中OpenSEES 計算結果后面出現了平直段，這主要是因為在拉索強度較高時，計算中主梁的彈塑性較強進而引起數值收斂困難造成的。圖10(b)中，OpenSEES 結果后面出現了近似平直段，主要原因是：主梁強度較高，拉索屈服時主梁可能還未出現塑性鉸，但數值計算不收斂、結構實際已失效進而導致極限載荷系數λu不再增加。

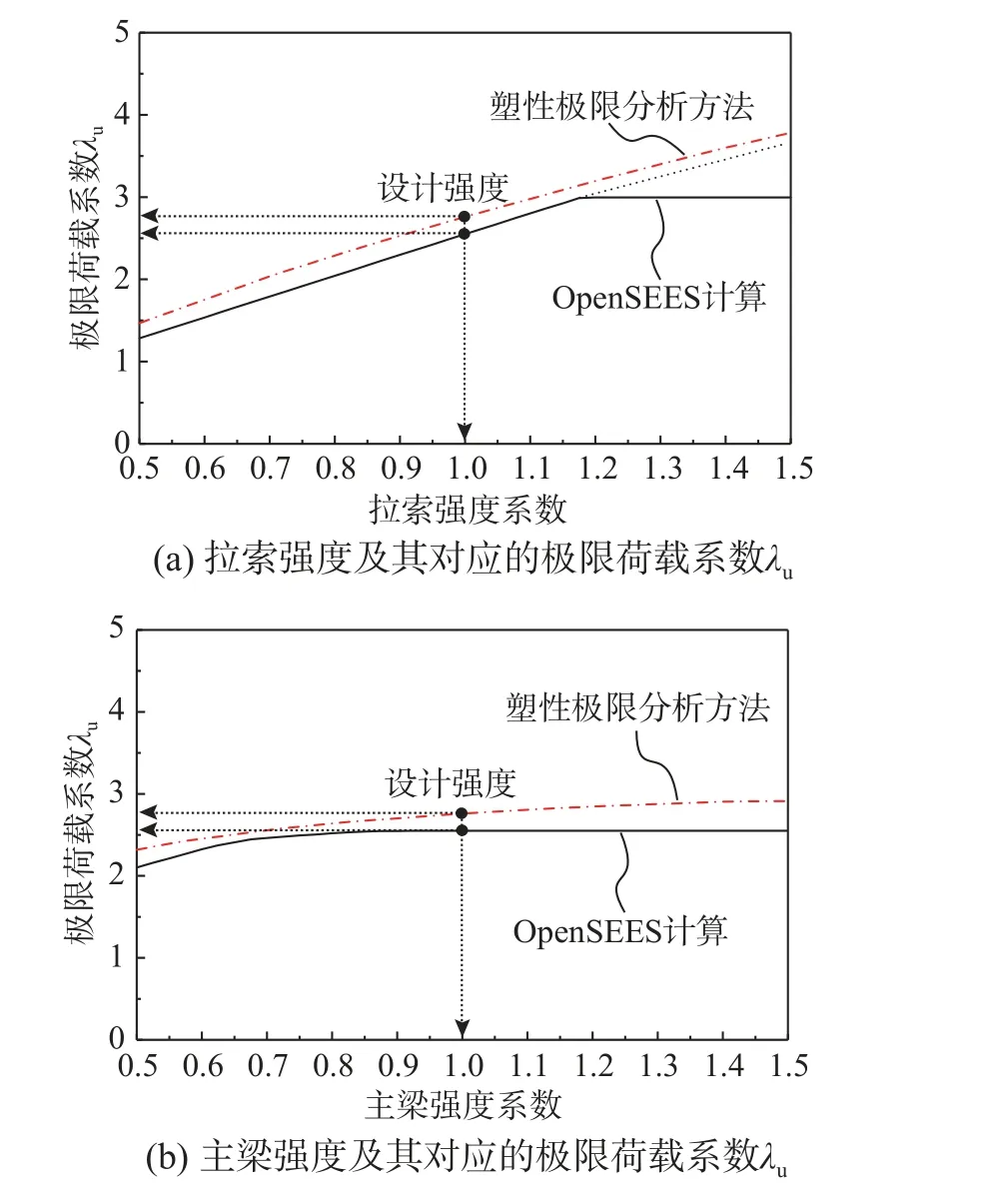
圖10 塑性極限荷載系數λu 對比(塑性極限分析法與OpenSEES)Fig. 10 Comparison of plastic ultimate load factor λu (plastic limit analysis method and OpenSEES)

以拉索和主梁設計強度為例(即拉索和主梁強度系數為1.0)，圖11 給出了飄浮體系斜拉橋兩種方法所得失效響應的對比分析。圖11 中左側為塑性極限分析法計算得到破壞結果，右側先由OpenSEES計算獲得結構的彈塑性響應，然后，忽略彈性變形轉化為純塑性的破壞結果。從圖11 可以看出，兩種方法計算所得的極限載荷系數λu分別為2.76和2.52，誤差約為8.7%；塑性鉸位置分別為114 m和96 m，誤差約為15.8%；屈服拉索數目分別為6 對和5 對，誤差約為16.7%。相比較而言，極限載荷系數λu的誤差要小一些。由圖11 中具體失效行為的對比分析可知，采用塑性極限分析法得到的結果有一定誤差，其主要來源有：① 方法本身的假定，如認為拉索屈服和塑性鉸形成同時發生；② 塑性極限分析法未能考慮主梁沿水平方向有限移動的影響；③ OpenSEES 分析時的數值收斂困難使其計算結果偏小。

圖12 給出了有限元結果中主梁若干節點的豎向位移(δv-86、δv-206及δv-300，86、206 及300 為節點號，位置如圖12 所示，以下相同)隨載荷系數λq的變化情況。由圖12 可得，隨λq的增加，δv-86基本呈現線性變化，這是因為該節點位于破壞機構范圍以外(圖11)，未達到屈服狀態；隨λq的增加，δv-206已呈現非線性增長，主要原因為該節點位于破壞機構范圍邊緣，已有一定的塑性變形(圖11)；隨λq的增加，δv-300后期變化呈現較強非線性，這是因為該節點位于索塔處(破壞機構范圍中間位置)，已產生較大的塑性變形(圖11)。

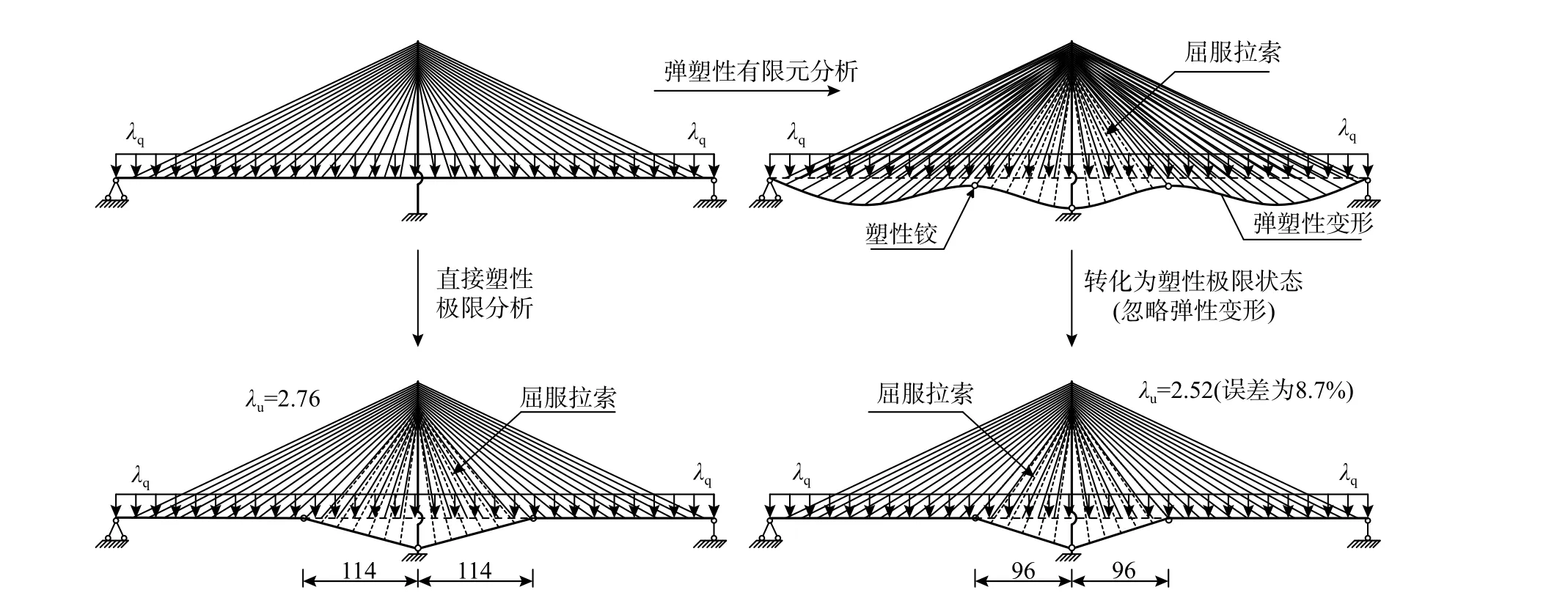
圖11 斜拉橋失效行為對比(塑性極限分析法與OpenSEES)Fig. 11 Comparison of failure behavior of cable-stayed bridge (plastic limit analysis method and OpenSEES)

圖13 為有限元結果中與上述節點對應處若干拉索及主梁截面內力隨載荷系數λq的變化情況。由圖13 可知，14C、15C、16C、17C 和18C 及右側對稱位置處的拉索已趨于屈服，對應位置處的主梁截面的彈塑性變形也不斷增加，這與圖12 的豎向位移變化是相對應的。

圖12 主梁節點豎向位移隨載荷系數λq 的變化Fig. 12 Variation of vertical displacement of girder with load factor λq

圖13 拉索和主梁截面內力隨荷載系數λq 的變化Fig. 13 Variation of internal force of cable and girder with load factor λq

圖12 和圖13 表明：隨著載荷系數λq的增加，索塔附近區域拉索內力、主梁節點位移、主梁截面內力都逐漸增加，離索塔越近，非線性越明顯。當荷載增至一定數值時，塑性變形及位移都急劇增加，直至打破結構平衡導致其失效破壞。

2.3 拉索銹蝕影響

上述分析結果表明：塑性極限分析方法可近似用于研究豎向荷載作用下飄浮體系斜拉橋的塑性倒塌荷載和失效模式。為此，本文嘗試應用該方法分析拉索銹蝕對斜拉橋結構失效機理的影響，這里主要探討單根拉索不同銹蝕程度的影響，拉索銹蝕假定見概述。

圖14(a)給出了飄浮體系斜拉橋單根拉索不同銹蝕程度對主梁塑性鉸位置的影響。圖14(b)描述了飄浮體系斜拉橋單根拉索不同銹蝕程度對極限荷載系數λu的影響。由圖14 可知，對于單根拉索銹蝕而言，僅有索塔附近至左右跨中間區域的拉索銹蝕對塑性鉸的位置有影響，且隨著銹蝕程度的增加，極限載荷系數λu逐漸降低，同時，能夠影響塑性鉸位置的拉索分布位置從索塔處逐漸向左右側擴展至跨中附近。圖14 表明：跨中至索塔處的拉索銹蝕對極限荷載系數λu和失效模式的影響較為顯著，且離索塔越近影響越突出，離索塔越遠影響越小，加之局部破壞時主梁塑性鉸也分布于此范圍內，因此，該范圍是導致斜拉橋結構失效破壞的關鍵區域。

圖14 單根拉索不同銹蝕程度下塑性鉸位置及極限載荷系數λu 的變化Fig. 14 Variation of position of plastic hinges and ultimate load factor λu with different corrosion of single cable

相比彈塑性有限元分析，塑性極限分析法只考慮結構的極限破壞狀態，且需要考慮較多的假定條件，因此其結果有一定的誤差，但影響規律是一致的。在有限元彈塑性分析中，屈服構件或截面是逐漸形成的，且只有在屈服拉索達到一定數量后，主梁才可能產生塑性鉸，這與塑性極限分析法是完全不同的。因此，在進行對比分析時，兩種方法對應結果的基本變化規律是一致的，但具體到某一數值上，誤差可能稍大些。

綜上分析可得，塑性極限分析法是一種簡化的計算方法，雖然，能夠快速便利的分析出各設計參數的變化對斜拉橋失效行為的影響，但誤差稍大，精度較有限元方法低一些。因此，該方法可用于斜拉橋初步設計階段，在快速計算出極限承載力的同時也識別出相應的倒塌模式，并在此基礎上修正相關設計參數，盡量避免不希望的失效模式的發生。

3 結論

本文基于理論推導和算例分析驗證了塑性極限分析方法用于研究豎向荷載作用下大跨度飄浮體系斜拉橋的極限承載力及其失效模式的可行性和適用性，在此基礎上分析了拉索銹蝕對斜拉橋結構失效行為的影響。主要結論如下：

(1)對于飄浮體系斜拉橋而言，當拉索強度與主梁強度之比相對較小時，斜拉橋主梁呈現出整體性破壞特點，類似于簡支梁的破壞形式；當拉索強度與主梁強度之比相對較大時，斜拉橋主梁以局部性破壞為主，且破壞區域位于索塔附近至跨中范圍內。從整體來看，拉索強度或主梁強度的改變都明顯改變著飄浮體系斜拉橋的失效行為，但極限載荷系數λu呈現出光滑連續的變化，而塑性鉸位置則呈現出臺階式的非連續變化，兩者之間明顯不同。分析結果表明索塔未出現塑性鉸破壞，這符合其結構特點，同時，也說明有限元分析時采用彈性梁柱單元是合適的。

(2)飄浮體系斜拉橋分析結果表明極限載荷系數λu的改變要更敏感于拉索強度的變化。考慮拉索銹蝕影響的分析表明拉索的銹蝕不僅降低極限載荷系數λu，還能改變塑性鉸的位置，也即改變著斜拉橋的失效模式。離索塔越近的拉索銹蝕對極限載荷系數λu及失效模式的影響越顯著，離索塔越遠的則影響越小。局部破壞時主梁塑性鉸及屈服拉索也多分布于索塔附近至跨中范圍內，因此，該范圍是導致斜拉橋結構倒塌失效的關鍵區域。

(3)結果分析表明：相比于有限元方法，塑性極限分析法可快速計算出極限載荷系數并識別出倒塌失效模式和關鍵構件，為斜拉橋初步設計階段相關設計參數的修正提供了一種簡化、快速及有效的計算方法。