ALE 方法在沉箱碼頭地震液化分析的應用

劉 順，唐小微，欒一曉

(大連理工大學海岸和近海工程國家重點實驗室，大連 116023)

重力式沉箱碼頭因其耐久性、方便建造而成為港口常見的濱水構筑物之一，在神戶港(Japan)、阿爾戈斯托港(Greece)、斯里蘭卡港 (SriLanka)等重要國際港口都有應用，我國青島港、廈門港、花蓮港(臺灣)等也有使用重力式碼頭。港口往往濱海或濱河建造，地基軟弱，為滿足承載力和穩定性要求，需采取地基處理措施以支撐上部結構物和工作載荷。圖1 為重力式碼頭的典型斷面形式，重力式碼頭的基礎和墻后通常使用砂土、碎石土等進行處理。

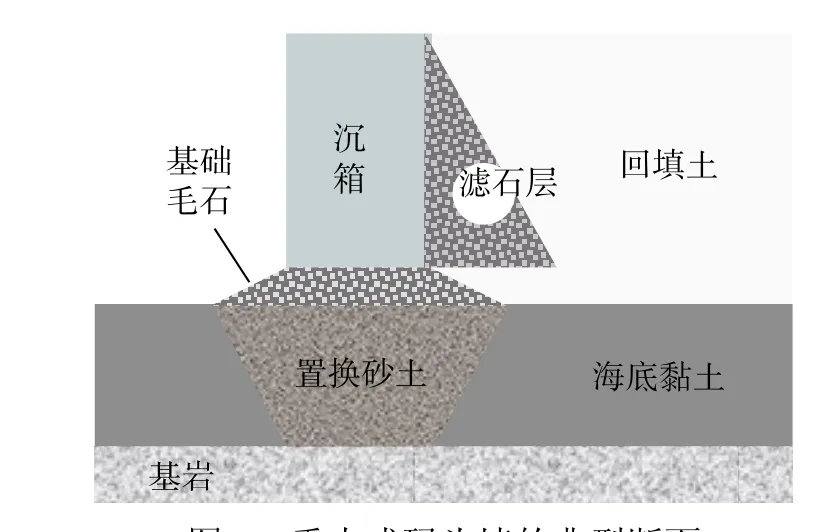
圖1 重力式碼頭墻的典型斷面Fig. 1 Typical section of gravity wharf

飽和砂土地基在地震發生時可能發生液化，進而引發結構破壞，因此飽和砂土液化及減防災措施研究始終是巖土工程領域研究的一個重點問題[1-6]。在過去幾十年，也有很多重力式碼頭墻遭遇地震液化破壞的記錄。1995 年，日本兵庫縣地震，神戶港碼頭的大量重力式沉箱結構遭到破壞，整個港口陷入癱瘓。此外，中國臺灣Chi-Chi 地震、土耳其Kocaeli 地震都觀測到重力式碼頭液化破壞的現象。破壞原因往往是基底置換砂和墻后回填土液化引起的碼頭墻沉降、向海側位移、傾斜等。

Abu 等[7]研究了地震作用下重力式碼頭土和結構相互作用，并分析了置換區和回填區密砂土實度對重力式岸壁結構的影響，Alyami 等[8]探究了滲透系數對重力式碼頭結構孔隙水壓力的影響以及回填土和地基土的相對密實度對岸壁殘余變形的影響。王麗艷等[9]詳細分析了液化地基中沉箱碼頭殘余變形隨各影響因素的變化規律，Tong 和Schaefer[10]研究了振沖加密優化設計對重力式碼頭墻液化災害的減弱作用。

上述研究均是基于有限元方法進行的數值模擬，作為一種有效的工具，有限元方法在工程領域有重要的應用。但在一些變形比較大的情況下，可能由于網格畸變導致計算中斷、精度喪失等。地震調查報告顯示，兵庫縣地震中神戶港區地面最大加速度達到0.6g，部分沉箱頂部水平殘余位移達5 m，殘余沉降達1 m～2 m，向海側傾角3°～5°。在強震作用下，基于傳統有限元方法的沉箱碼頭動力分析可能由于較大的變形引起分析中斷或者結果失真，不能合理反映強震作用下沉箱碼頭的最終變形，難以對沉箱碼頭的抗震優化設計起到有效的參考作用。基于算子分裂技術和自主開發的水土耦合動力液化數值分析平臺，筆者發展了一種ALE 有限元方法，并通過飽和土柱一維固結和離心機模型試驗模擬進行了驗證[11]，詳細實現過程可參考文獻[11]，這里將其用于強震作用下的沉箱碼頭地震液化分析。

1 飽和砂土控制方程

基于水土二相混合理論，以土骨架位移u和孔隙水壓力p作為變量，Uzuoka[12]推導了u-p形式的飽和砂土的場方程式：

2 ALE 方法簡介

基于拉格朗日描述的有限元方法可能由于網格畸變導致計算中斷、精度喪失，而基于歐拉描述的有限元方法處理運動的物質邊界和相互作用問題是十分困難的。結合兩種方法的優點，Donea 等[15]發展了一種任意的拉格朗日歐拉方法(Arbitrary Lagrangian Eulerian Method) 用于解決流體力學問題，隨后該方法被眾多學者用于解決固體力學中的非線性問題。

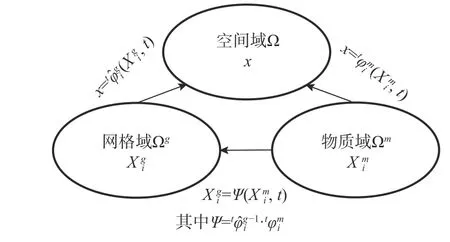
圖2 物質域、網格域、空間域之間的映射關系Fig. 2 Mapping relationship among material domain, grid domain and spatial domain

根據ALE 方法的實現途徑，可以將其分為兩類：1) 完全耦合的(Fully Coupled)；2) 解耦合的(Decoupled)。完全耦合的ALE 方法將式(8)代入基于計算域的控制方程進行線性化，將物質運動和網格運動整合于離散化的有限元方程中，其基本形式如式(9)[16]所示：

式(10)中，耦合的ALE 方法需事先指定物質點和網格點的運動關系，這種關系通常比較簡單，如超限映射法[17]等，對于結構形式復雜或變形較大的情況，往往不能作為有效的解決方案。在實踐中，解耦合的ALE 方法更為普遍，該方法基于算子分離技術將一個完整的ALE 分析步分解為[18]：1) 忽略網格和物質相對運動的拉格朗日分析步，即更新拉格朗日方法；2) 將場變量在物質域和網格域之間傳遞的歐拉分析步。本文發展的ALE 有限元方法是在課題組開發的更新拉格朗日格式的水土耦合地震液化分析平臺基礎上，基于算子分離技術的解耦合ALE 有限元程序[11]。

3 有限元模型

3.1 模型簡介

本文考慮了邵琪[19]在飽和砂土地震液化網格自適應的研究中采用的兩種重力式碼頭地基處理形式。如圖3 所示，沉箱位于海底黏土之上，沉箱底部用砂土置換，沉箱后部以砂土回填，兩種方案不同之處在于沉箱地基的置換范圍和形式。兩種方案中，模型兩側邊界設置寬高比較大(＞100)的單元和等位移邊界(EDB)模擬自由場邊界[11]，兩側邊界和底邊界為不透水邊界，模型頂部(粗虛線)可自由排水。各區域的尺寸見文獻[19]。

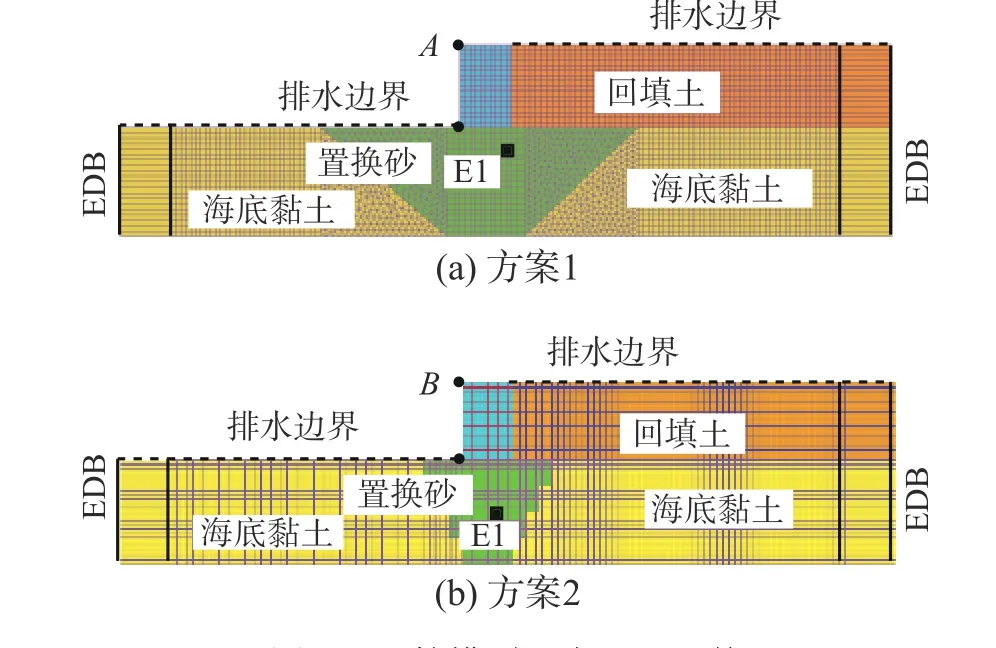
圖3 沉箱模型及有限元網格Fig. 3 Caisson model and Finite element meshes

3.2 輸入地震動

文中選擇Kobe (Japan，1995，PA=0.834g)，Kocaeli (Turkey，1999，PA=0.349g)，Northridge(USA，1994，PA=0.568g) 三種地震波作為輸入荷載，如圖4 所示。圖中，左側為地震波，右側為對應傅里葉譜，其中Kocaeli 波的主要頻率范圍低于1 Hz，Kobe 和Northridge 波的主要頻率范圍在1 Hz～10 Hz。考慮豎向地震動的影響，取水平向輸入荷載的1/2 作為豎向地震動輸入。

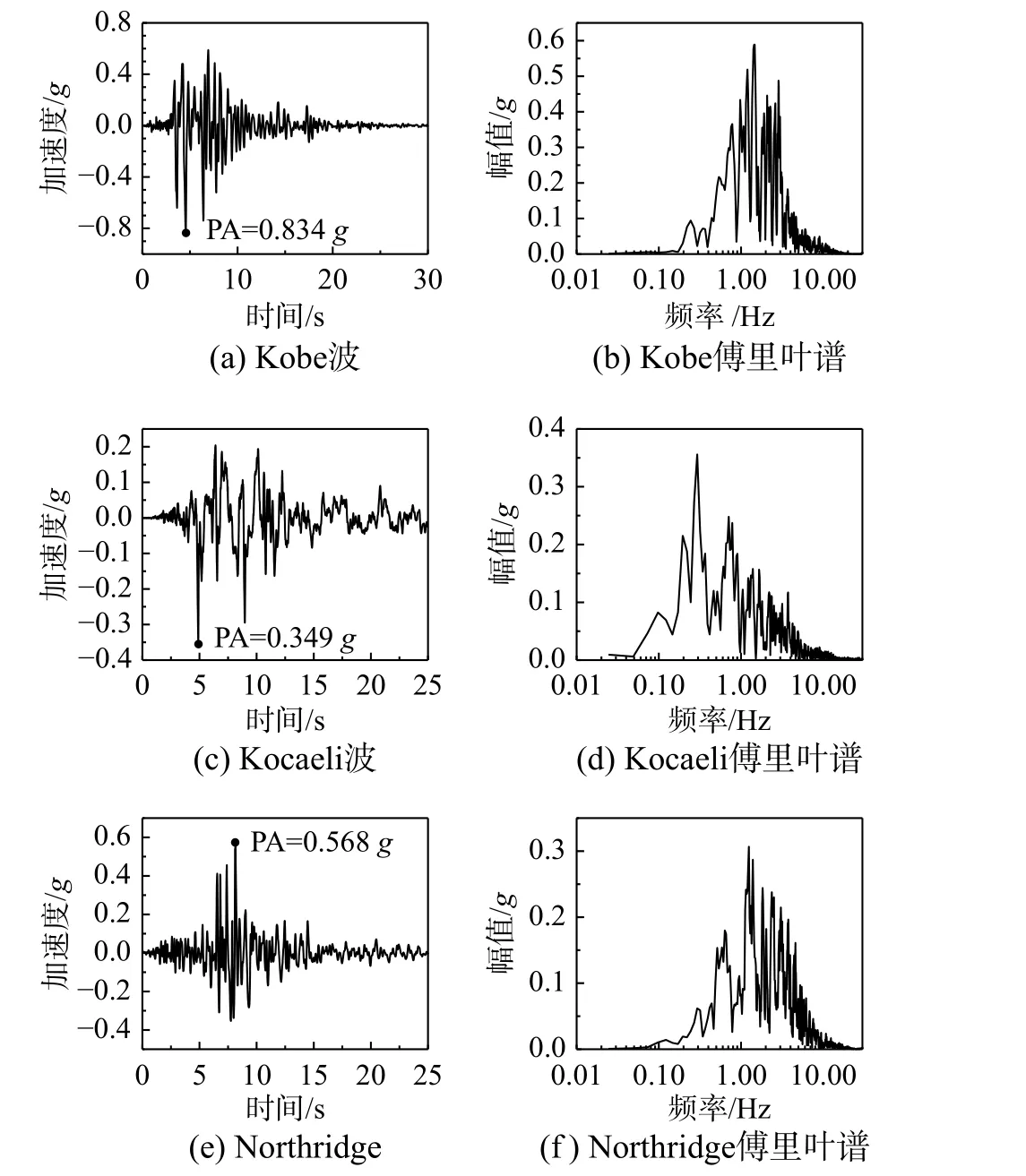
圖4 地震波加速度及傅里葉譜Fig. 4 Acceleration and Fourier spectra of earthquake waves

圖5 為近幾十年來，記錄的一些地震的峰值加速度分布，可以看出，強震動峰值加速度主要集中在0.5g左右。因此，本文對于強震動作用下沉箱碼頭的地震液化分析，所采用的三種地震波時程將按照其峰值強度與0.5g的比例進行調整到0.5g。

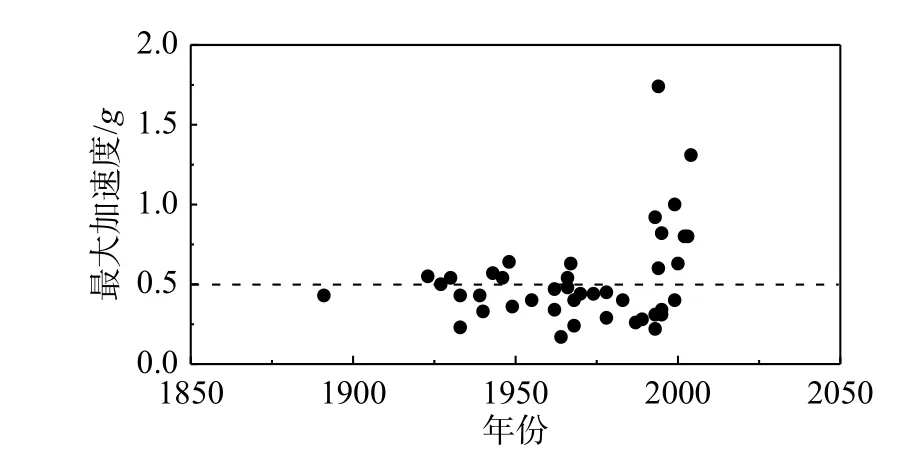
圖5 近幾十年地震最大加速度[22]Fig. 5 Peak acceleration of earthquakes in recent decades[22]

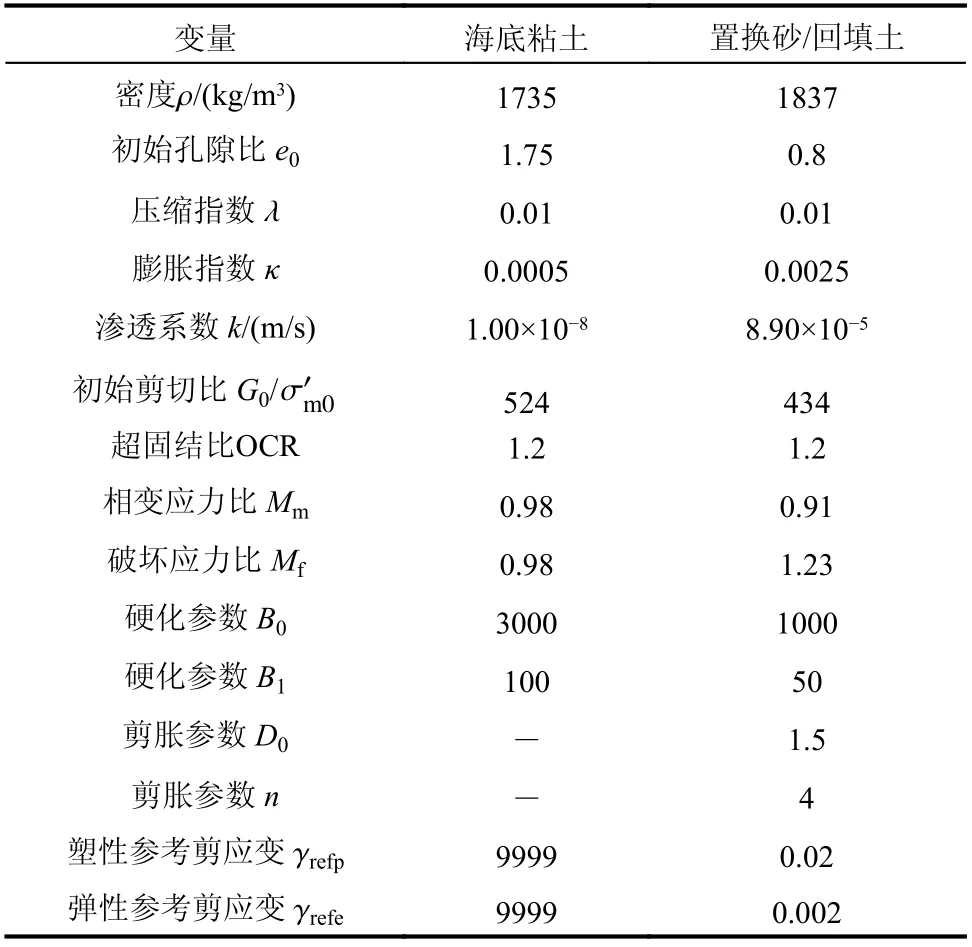
表1 模型參數Table 1 Model parameters

4 數值結果分析

4.1 網格形狀

圖6 和圖7 顯示峰值加速度為0.5g時，兩種方案在三種地震荷載作用下，最終的網格變形，左側為ALE 方法的網格，右側為UL 方法的網格。

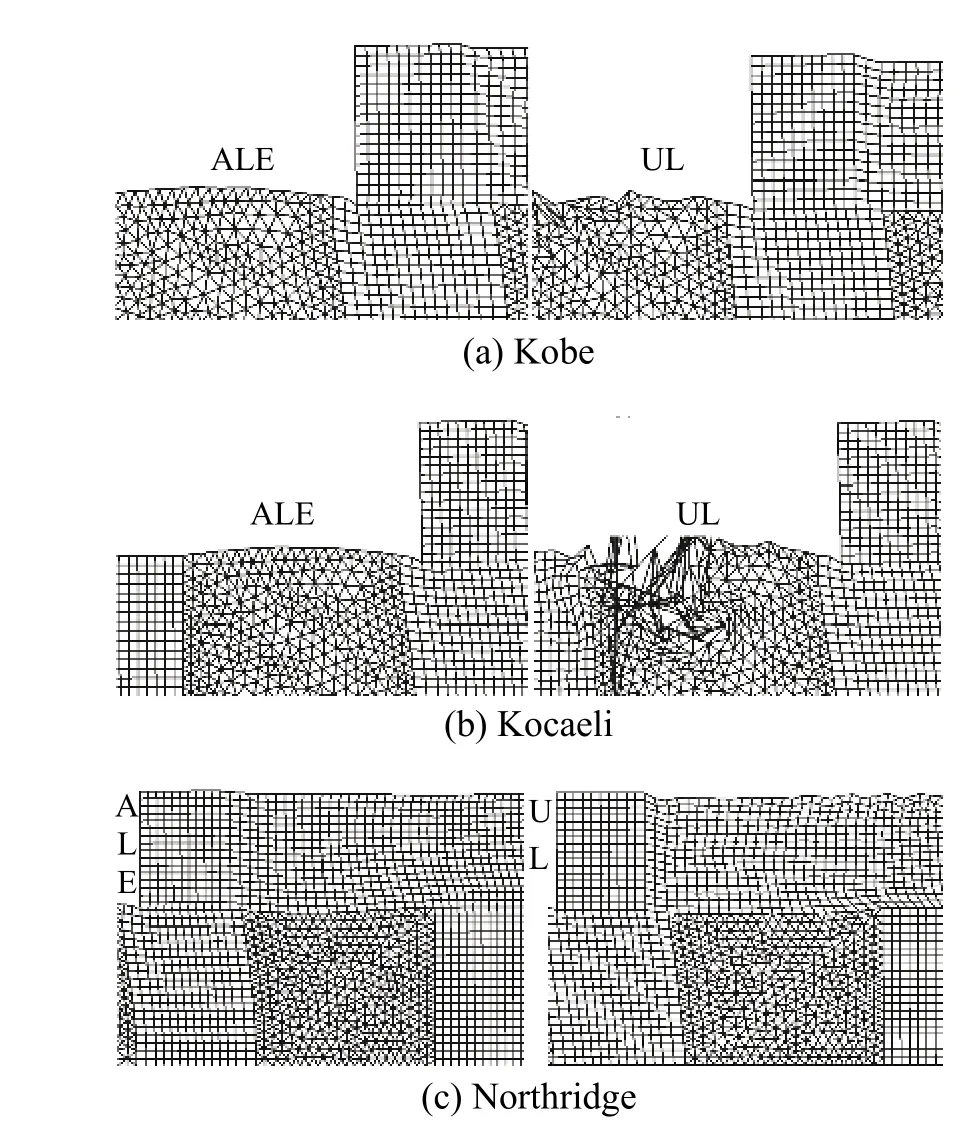
圖6 方案1 網格變形圖(Peak=0.5 g)Fig. 6 Mesh deformation of Case 1 (Peak=0.5 g)

圖6 顯示，方案1 中使用UL 方法的沉箱趾部前端在Kobe 波和Kocaeli 波作用下發生大范圍的網格畸變，沉箱墻體后方的回填區在Northridge 波作用下存在局部的網格畸變；ALE 方法中網格在三種地震荷載作用下均處于健康的狀態。

圖7 顯示，方案2 中在三種地震波作用下，UL 方法在沉箱趾部前端局部(Kobe)和較大范圍(Northridge)以及墻體后部(Kocaeli)產生網格畸變，導致該方法失效；ALE 方法僅在沉箱趾部發生局部網格變形，整體網格處于健康狀態。需要說明的是，在Kocaeli 波作用下ALE 方法失效是由于方案2 中沉箱發生較大的傾斜，置換區產生較大隆起變形，沉箱趾部侵入置換區，導致局部網格由凸變凹，同時也反映出此種處理方案下，沉箱在強震作用下的變形特點。

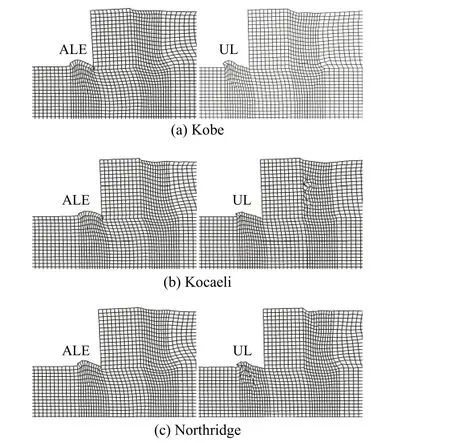
圖7 方案2 網格變形圖(Peak=0.5 g)Fig. 7 Mesh deformation of Case 2 (Peak=0.5 g)

綜合圖6 和圖7，ALE 方法能夠在強震作用下保持沉箱結構網格的整體質量，從而保持計算的持續性和準確性，反映沉箱結構的變形特點；UL 方法在強震作用下可能由于結構的大變形引起網格畸變導致數值方法失效。

4.2 殘余位移

圖8 為三種地震荷載作用下，方案1 沉箱頂點(圖3(a)A點)在不同峰值加速度下的水平位移。可以看出，在峰值加速度PA=0.1g時，加載初期變形較小，兩種方法的沉箱頂點位移基本一致，隨著加載進行，UL 方法的頂點殘余位移稍大于ALE 方法。強震作用時(PA＞0.3g)，兩種方法對應的沉箱頂點位移隨著加載進行差異明顯，并且峰值加速度越大差異越大。圖8(a)、圖8(b)顯示，在強震作用下，由于沉箱變形太大引起網格畸變導致UL 方法失效而不能完整反映沉箱位移變化，而ALE 方法則完整反映了沉箱頂點位移變化，并提供了最終的沉箱殘余位移。圖8(c)中，在Northridge 波作用下，UL 方法和ALE 方法均能反映沉箱頂點位移變化過程，但二者的差異隨峰值加速度增大而變大。需要指出的是，強震時ALE 方法對應的沉箱頂點最終位移高于UL 方法中斷時對應的位移。如表2 所示，在Kobe 和Kocaeli 波作用下，二者的位移差值最大達16%。

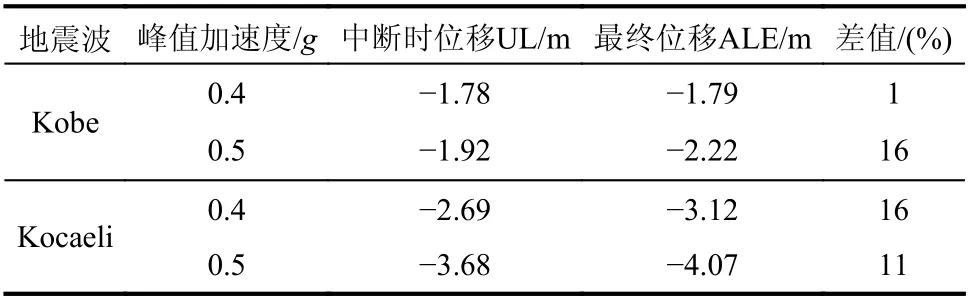
表2 方案1 沉箱頂點位移Table 2 Displacement of caisson apex of Case 1

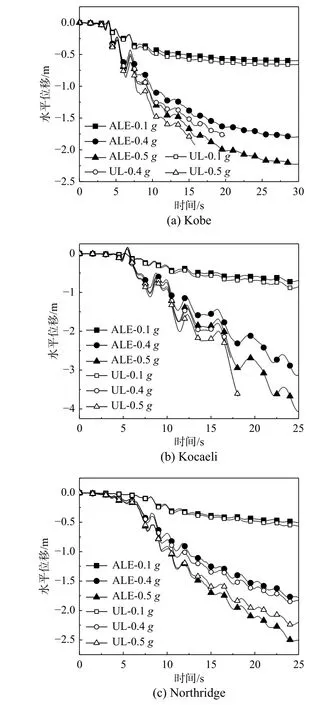
圖8 沉箱頂點水平位移時程(方案1)Fig. 8 Horizontal displacements of caisson apex of Case 1

圖9 為三種地震荷載下，方案1 沉箱頂點在不同加速度峰值下ALE 方法的殘余水平位移(圖9(a))和豎向位移(圖9(b))。從圖中可以看出，沉箱的殘余位移與地震荷載峰值加速度近似呈線性關系，與文獻[9]中殘余位移與輸入荷載相關性一致。Abu 等[7]指出低頻荷載對應的沉箱碼頭向海側位移相對更大。可以發現，圖9 中Kobe 波和Northridge 波對應的殘余位移增長率相似，且數值相近，而Kocaeli 波作用下，殘余位移隨峰值加速度的增長率高于其他兩種地震波，且強震時相同峰值加速度對應的殘余位移遠高于其他兩中地震波對應的殘余位移。考慮到輸入荷載的頻譜特性，沉箱碼頭的地震響應受低頻地震波影響更大，這與文獻[7]的結論一致。

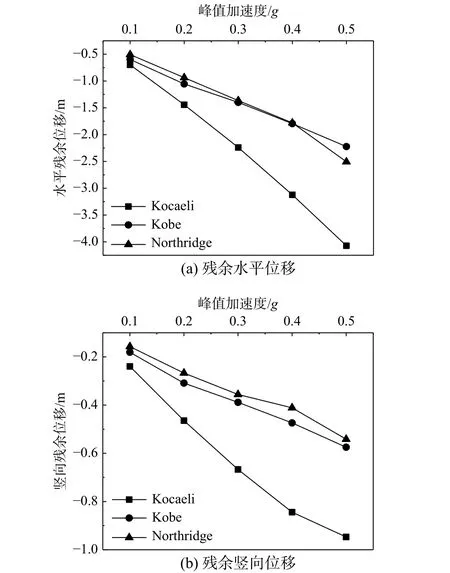
圖9 沉箱頂點殘余變形(方案1)Fig. 9 Residual displacements of caisson apex of Case 1

圖10 所示為三種地震荷載作用下，方案2 中沉箱頂點(圖3(b)B點)在不同峰值加速度下的水平位移。在小震(PA=0.1g)和強震(PA＞0.3g)作用下，方案2 沉箱頂點位移均勻與方案1 的沉箱頂點位移發展趨勢相似。不同之處在于，方案2在強震(PA＞0.3g)作用下，UL 方法失效時間比方案1 有所提前，并且ALE 方法在一些情況下(Kobe波PA=0.5g和Kocaeli 波PA=0.4g、0.5g)也發生失效。不同于UL 方法導致的大范圍網格畸變，ALE 方法失效的共同特點是由于沉箱向海側傾斜，侵入置換砂地基導致沉箱趾部某些網格失效(圖7)，并未影響網格的整體質量。此種情況下，除更換整體網格或計算方法外并無有效解決途徑。此外ALE 方法失效時，均已超過了輸入地震波的主震范圍，震動基本結束，且殘余位移水平已經遠超沉箱碼頭正常工作所允許的范圍，此時的殘余位移對于沉箱碼頭抗液化措施有效性評價仍具有參考意義。表3 為在峰值加速度為0.4g和0.5g的Kobe 和Northridge 波加載下，UL 方法和ALE 方法在計算中止時對應的沉箱頂點位移，可以看出在方案2 情況下，ALE 方法的位移遠大于UL 方法，最大差值達56%。

圖10 沉箱頂點水平位移(方案2)Fig. 10 Horizontal displacements of caisson apex of Case 2

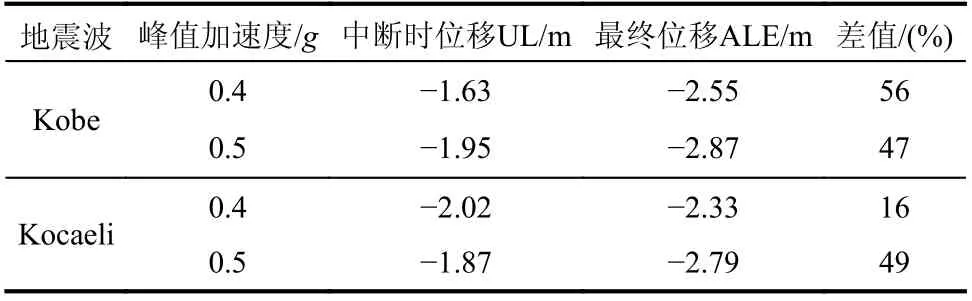
表3 方案2 沉箱頂點位移Table 3 Displacement of caisson apex of Case 2

圖11 為三種地震荷載作用下，方案2 中沉箱頂點在不同峰值加速度下使用ALE 方法的殘余水平位移(圖11(a))和豎向位移(圖11(b))。與方案1中結果相似，沉箱殘余位移與地震波峰值加速度近似呈線性關系，并且Kocaeli 波的殘余位移大于Kobe 波和Northridge 波，反映出沉箱地震響應的低頻敏感性。文獻[7]中顯示地基處理方案對將沉箱碼頭系統的模態頻率有較大影響，具體表現為隨著置換區地基區域的變大，模態頻率逐漸變大；沉箱碼頭墻底部置換區加固對模態頻率的影響高于沉箱碼頭墻后回填區。由圖9 和圖11 可以看出，在相同峰值加速度下，方案2 中Kobe 波和Northridge 波對應的殘余位移大于方案1，這是由于地基處理方案的不同，改變了沉箱碼頭的自然頻率，使得沉箱碼頭對Kobe 波和Northridge 波的地震響應變大，也減小了Kocaeli 波的地震響應與Kobe 波Northridge 波地震響應的差距。

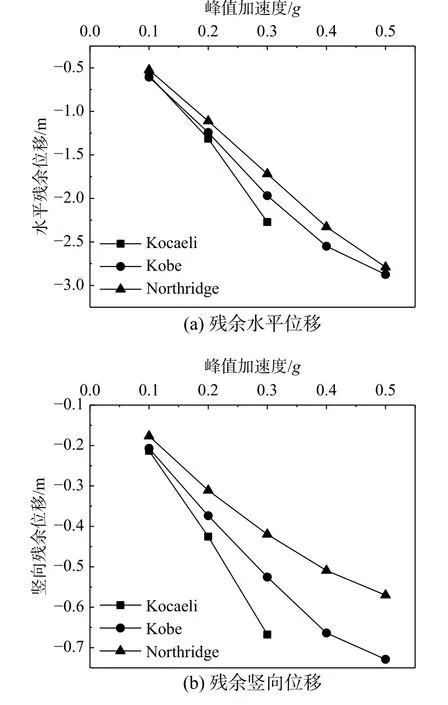
圖11 沉箱頂點殘余變形(方案2)Fig. 11 Residual displacements of caisson apex of Case 2

4.3 相對誤差分析

在地震液化的數值分析中，土體和結構由于液化引起的變形是關注的重點，因此，本文將單元應變作為誤差評估對象來評估UL 方法和ALE方法在地震液化計算中對計算結果的影響。基于應變的平均相對誤差定義形式可參考文獻[19]。

圖12 顯示，方案1 中，在小震(PA=0.1g)作用時，除初期兩種方法的相對誤差相差不大以外，UL 方法平均相對誤差隨著變形增大而持續增大，ALE 方法對應的平均相對誤差處于很低的水平。強震(PA＞0.3g)作用下，計算初期兩種方法的平均相對誤差亦差別不大。隨著變形的增大，UL 方法對應的平均相對誤差持續增大，在計算失效時，相對誤差出現陡升，對應圖6 中大范圍的網格畸變，而ALE 方法則保持平均相對誤差始終處于較低的水平，直至計算結束。

圖13 顯示，方案2 中，小震作用下，UL 方法和ALE 方法的相對誤差發展趨勢與方案1 相似。強震(PA＞0.3g)作用下，UL 方法計算失效，對應了圖7 中部分網格畸變，ALE 方法在Kobe 波和Kocaeli 波作用下盡管比UL 方法計算持時較長，也未能完成整個計算過程。如第4.2 節所述，ALE 方法失效但并未影響整體網格質量，從圖13可以看出UL 方法失效時，由于較多網格畸變，平均相對誤差出現陡升，而ALE 方法雖然失效，平均相對誤差始終處于很低的水平，且未出現由于大范圍網格失效導致的誤差陡增。

綜合圖12 和圖13，ALE 方法用于沉箱碼頭的地震液化分析，在保證網格質量的基礎上，提供了相比UL 方法精度更高的結果。

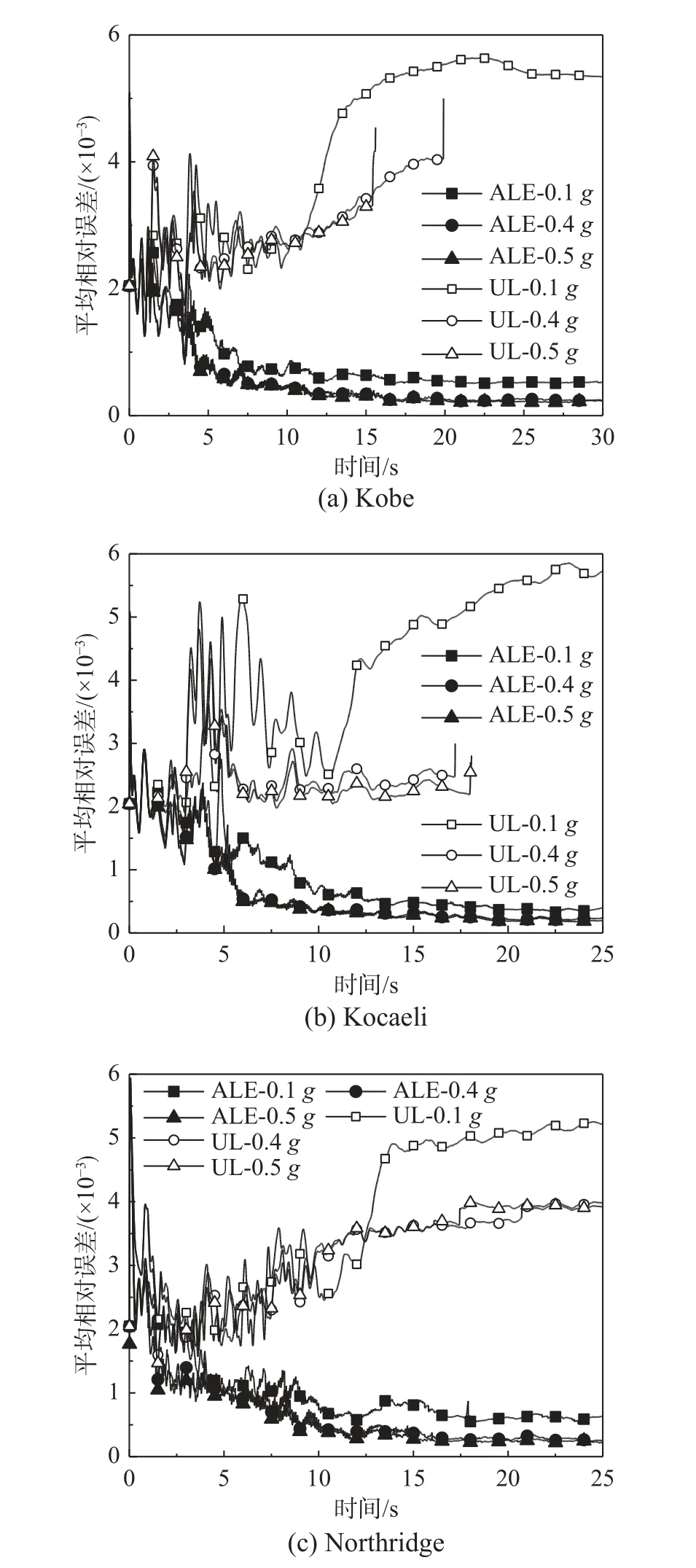
圖12 平均相對誤差曲線 (方案1)Fig. 12 Average relative error curves of Case 1

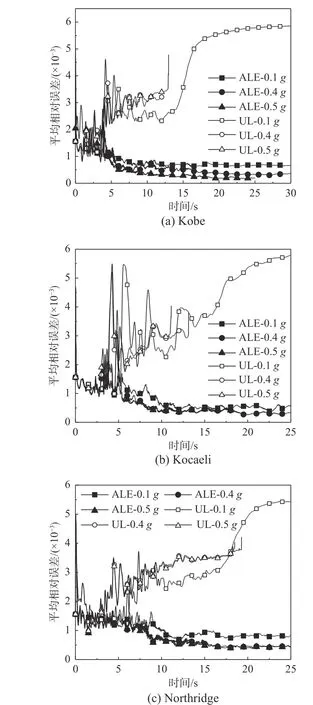
圖13 平均相對誤差曲線 (方案2)Fig. 13 Average relative error curves of Case 2

4.4 超孔隙水壓力

為表征飽和砂土在地震作用下的孔壓水平，這里定義超孔隙水壓力比(excess pore water pressure ratio)為EPWPR=Δu/σ′y0，其中， Δu為單元超孔隙水壓力， σ′y0為單元當前豎向有效應力。

圖14 為方案1 在不同峰值的Kocaeli 波(0.3g～0.5g)作用下，ALE 方法中E1(圖3(a))的超孔壓比曲線和云圖。從圖14(a) 可以看出在不同峰值作用下，E1 的超孔壓水平都較低，未達到液化水平。整體來看，孔壓發展在該地震波激勵下波動較為劇烈，0.5g對應的孔壓曲線加載后期與0.3g和0.4g相差較大，達到較高的水平。從圖14 超孔壓云圖可以看出，隨著峰值加速度的增大，沉箱底部雖未達到液化，但高超孔壓區逐漸擴展。回填區液化主要發生在距離墻后一定距離的區域，緊鄰碼頭墻后方區域未發生液化，這種現象與實際地震中墻后液化現象一致[23]。隨著峰值加速度增大，回填區和置換區的高孔壓區逐漸產生連通，這將加大沉箱的殘余變形，因此，設計中可考慮設置阻斷置換區和回填區孔壓轉移的措施，如振沖加密置換回填區土體[10]或設置水平止水層。

圖15 為方案2 在不同峰值的Northridge 波(0.3g～0.5g)作用下，ALE 方法中E1(圖3(b))的超孔壓比曲線和云圖。方案2 中E1 孔壓隨加載進行逐漸累積，且峰值加速度增大，相應超孔隙水壓力越大。圖15 云圖顯示在方案2 的沉箱下部，有較大范圍的液化區，隨著峰值加速度的增大，液化區范圍逐漸增大，并且有與圖14 類似置換區和回填區高孔壓區貫通擴展的現象。方案1 沉箱底部未出現明顯液化區，而方案2 沉箱底部存在較大范圍的液化區，說明方案2 的形式在沉箱底部易產生孔壓積聚。

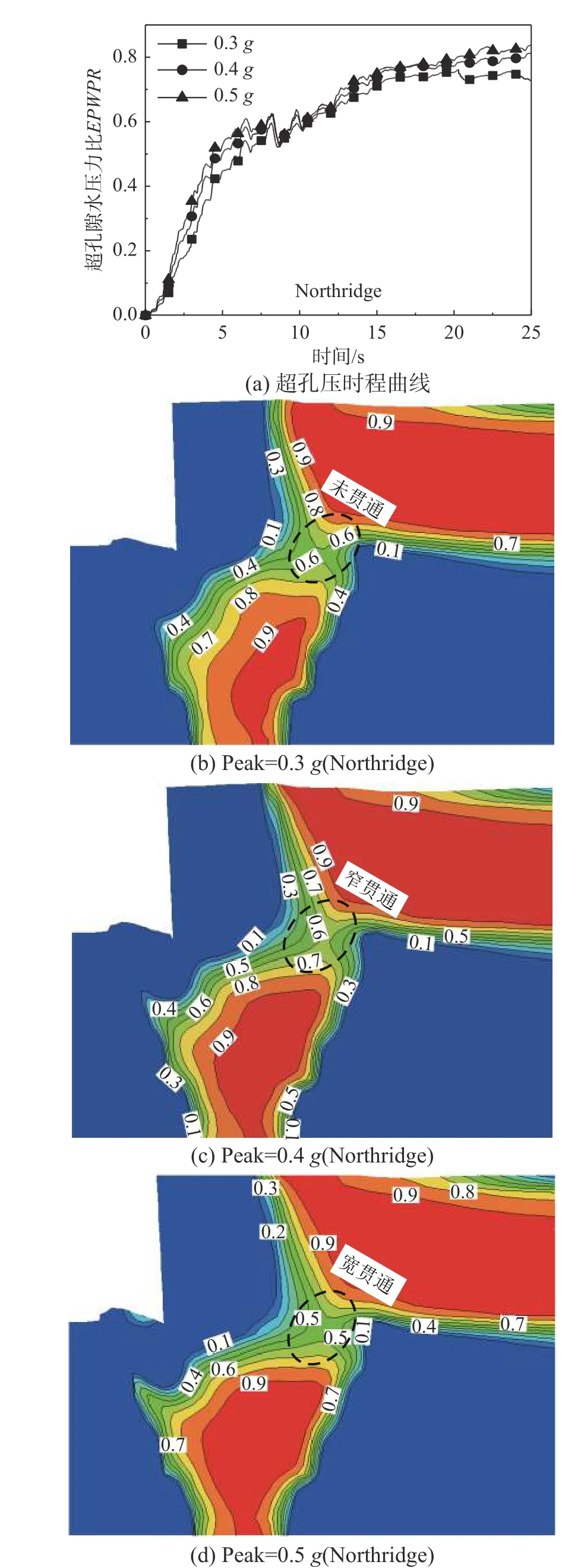
圖15 超孔隙水壓力曲線和云圖(方案2)Fig. 15 Curves and contours of EPWPR (Case 2)

5 結論

基于飽和砂土控制方程和算子分裂技術，發展了一種解耦和的ALE 有限元方法，并將其用于飽和砂土地基沉箱碼頭地震液化分析。使用UL 方法和ALE 方法對比了兩種沉箱地基處理方案在三種不同地震波激勵下的地震響應，主要結論如下：

(1) 小震作用下，UL 方法和ALE 方法均能完成分析，并且UL 的計算結果略大于ALE 計算結果；強震作用下，UL 方法失效引起計算中止時的沉箱頂點位移與ALE 方法完成計算時相差較大。因此，文中發展的ALE 方法可用于對于UL方法不能夠提供完整的沉箱碼頭地震響應的情況。此外，相對誤差分析結果顯示，無論UL 方法是否能完成計算，ALE 方法的平均相對誤差均低于UL 方法，表明ALE 方法能夠提供精度可靠的數值解。

(2) 沉箱碼頭的殘余位移與地震加速度峰值近似呈線性關系，且對低頻的荷載較為敏感，相應的地震響應也較大。地基處理方案不同將改變結構的自然頻率，進而影響沉箱碼頭對地震荷載的敏感頻率范圍。因此，在沉箱碼頭的設計中，應考慮地基的處理形式對自然頻率的影響，進而影響到沉箱碼頭的地震響應。

(3) 置換區和回填區在地震荷載作用下，可能存在高孔壓連通區，并且地震峰值加速度越大，連通區范圍越大。連通區將增大沉箱碼頭地震響應的殘余位移，因此，在設計中，可考慮設置阻斷置換區和回填區孔壓轉移的措施。