人行橋人致橫向振動的新型模型—IP-K 模型

賈布裕，茅思奕，陳揚文，顏全勝，余曉琳

(華南理工大學土木與交通學院，廣東，廣州 510640)

自從英國千禧橋及法國Solferino 橋等一系列人行橋大幅橫向振動事件發生后，雖然人們已經開始廣泛關注并研究人行橋的振動安全問題[1-14]，但事實上目前關于人行橋橫向大幅振動的機理仍未得到明確的解釋。關于人行橋橫向大幅振動的機理，目前主要有2 大類較為受歡迎的模型：一種是同步鎖定模型(synchronization locked model，SLM)；一種是倒擺模型(inverted pendulum model，IPM)。SLM 中具有代表性的有Fujino 的線性直接共振模型[11-12]和Strogatz 的相位同步耦合模型[15-17]。線性直接共振模型一般假設行人激勵與橋梁響應無關，將橋梁大幅度橫向振動視為由行人橫向步頻與橋梁某階頻率一致引起共振而造成，其中單人橫向荷載可采用簡諧函數表示。Strogatz 提出的相位同步耦合模型，其背景理論為生物學中的振子同步耦合理論，核心模型是日本學者Kuramoto提出的Kuramoto 模型[18-20]。起初，Kuramoto 模型研究對象是生物學中的“擺動將和同步相隨”問題，如夜晚中螢火蟲群體同步閃爍現象。Strogatz巧妙地將這一理論應用到了人行橋橫向振動中[15]，建立了橋梁振動和人群個體相位變化耦合的方程組，并利用該模型的穩定條件解釋了橋梁發散失穩現象。SLM 的核心假設是行人行走行為(尤其是步頻)會受橋梁振動影響發生變化。當橋梁振動影響到行人行走舒適性的時候，行人的步頻將發生變化，趨向于和橋梁振動同步，導致橋梁振動進一步增強；而橋梁振動增強時，又會進一步刺激更多的人群參與到與橋梁振動同步中，繼而使橋梁振動更加明顯，形成一個惡性循環。IPM 由Macdonald 等[5,21]提出。基于Mackinnon 等[22]和Hof 等[23]的人體平衡學，Macdonald 近似地把行人等效為一個由2 個交替的剛性桿支撐的質量體，并將行人橫向力視為受人體平衡策略控制的重心慣性力，他認為行人是依靠調節步伐位置而不是步頻來維持本身的舒適和平衡，而這個平衡控制策略來源于Hof 等[23]提出的人體平衡策略，即人體質心不會超過足壓中心，并保有一定的安全裕度。值得注意的是，IPM 與SLM 的不同之處在于，其認為行人是依靠調節步伐位置而不是步頻來維持本身的舒適和平衡，換言之，IPM 認為人-橋相互作用引起的自激力同樣足夠引起橋梁振動失穩，而行人同步鎖定并不是橋梁振動失穩的前提條件。

除了理論基礎不同，SLM 和IPM 還存在一個很大的不同：SLM 大部分是基于現場試驗的宏觀模型，而IPM 則屬于基于室內試驗的微觀模型。事實上，一直存在著關于宏觀模型和微觀模型孰優孰劣的爭論：微觀模型本質上是一種基于數據反推的模型，無法正確描述橫向大幅振動機理，采用微觀模型者往往認為宏觀模型過于粗糙，宏觀模型得到的結果數據并不一定能反映實際情況；而采用宏觀模型者則認為微觀模型的試驗環境和現場不一致(如人群效應、橋梁環境對行人行為的影響)。從既有的研究來看[9,21,24-28]，IPM 更具普適性。但IPM 存在著一個被質疑的問題：采用IPM 得到的對應于正常步頻的速度同相自激力分量系數cp(或稱為行人施加等效阻尼系數)遠小于實測值(這導致其計算得出的振動失穩臨界人數遠大于實測人數)，如圖1 所示。產生這個問題的根源在于，IPM 產生于室內試驗環境，只能考慮單人在特定振動平臺上(一般采用改裝跑步機)的行走特性，不能考慮人群在實際橋梁中的行走特性，尤其忽視了真實存在的人群同步效應 (而這正是SLM 模型中的理論假設)。因此，有必要考慮兼容SLM 和IPM 的可能性。事實上，McRobie 的研究工作[29]已表明：如果在IPM 中考慮同步效應將會使其結果更合理些。遺憾的是，McRobie 雖然認識到了這點，但他并沒有給出如何在IPM 中考慮同步效應的方法[29-30]。

圖1 IPM 的cp 和實橋測試所得cp[1,31]Fig. 1 Curve of cp [1,31] predicted by IPM compared with those obtained from full-scale measurements

啟發于McRobie 的工作，本研究提出了一種新型人行橋人致橫向振動模型：IP-K(inverted pendulum―Kuramoto)模型。在所提模型中，采用McRobie 方法得到的考慮長期效應的IPM 解析解(正常情況下IPM 無解析解)，同時引入相位同步耦合模型—Kuramoto 模型(以便考慮同步效應以及橋梁振動對行人同步效應的影響)，經過細致推導，獲得改進的IPM 模型(即IP-K 模型)。

1 IPM 長期效應解析解

1.1 IPM 模型

1.2 IPM 的長期解

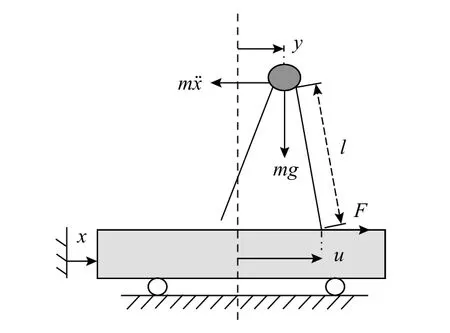
圖2 行人倒擺模型Fig. 2 Inverted pendulum model

2 相位同步耦合模型

2.1 Kuramoto 模型

Kuramoto 模型最初起源于集體同步現象研究：一個規模較大的振子系統自發地鎖定在一個共同的頻率上，盡管每個振子的固有頻率存在著差異[35]。生物學上的例子包括：心臟起搏器細胞網絡；同步閃爍的螢火蟲群；蟋蟀齊聲鳴叫等。在物理學和工程學中也有許多例子，如激光陣列和微波振蕩等。集體同步在自然界中無處不在，一般被認為它與大腦中阿爾法節奏的產生有關。對集體同步問題研究具有開創性貢獻的是日本學者Kuramoto[18]，他用攝動平均法證明了任何弱耦合的動力長期演變系統都可由以下的一般性相位方程給出：

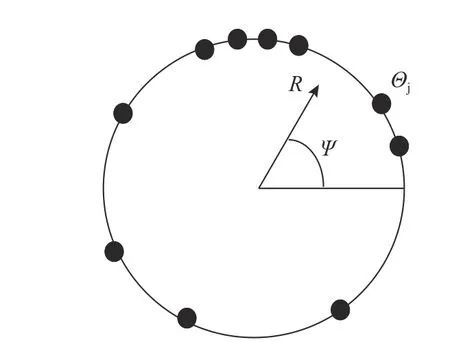
圖3 序參量示意圖Fig. 3 Schematic of order parameter

2.2 基于Kuramoto 模型的橋上行人相位演化

相位同步耦合模型的基本思想是：系統中的各個振子頻率最初是隨機分布的，但如果外部刺激足夠強大或者初始頻率接近于中心控制頻率時，各個振子頻率將會與中心控制頻率同步，并被鎖定。行人作為一個生物體，受到橋梁振動或者其他周圍行人運動影響刺激時，同樣會發生人-橋同步鎖定或者人-人同步鎖定。本研究將只注重于人-橋同步鎖定，暫不考慮人-人同步鎖定。在人-橋同步鎖定中，橋梁振動響應(幅值、速度、加速度)是對行人產生影響的刺激源，因此，在式(11)基礎上，基于Kuramoto 模型的橋上行人相位演化可寫為：

Θ˙i=ωi+Z(A,x˙,x¨)sin(Ψ-Θi),i=1,2,···,N(12)

式中：ωi為行人初始步頻； Θi為行人運動當前相位， Ψ為橋梁振動相位。Strogatz 將橋梁振幅視為刺激源[15](Z(A,x˙,x¨)=EA)：

Θ˙i=ωi+EiAsin(Ψ-Θi),i=1,2,···,N(13)

其中，Ei為行人對橋梁振幅A的敏感系數。Eckhardt則將橋梁振動加速度視為刺激源[16]：Z(A,x˙,x¨)～x¨。本研究只考慮將橋梁振幅A視為刺激源的情況，同時設每個行人對橋梁振幅的敏感系數相等，即Ei=E。為直觀展示相位演化過程，圖4 給出了行人分別在橋梁零振幅、較大振幅諧波振動下的行人相位演化軌跡圖(行人步頻和橋梁振動頻率的初始比值為1.05)。圖4(a)對應的是橋梁振動幅度為零的情況，此時行人運動不受橋梁振動影響，兩者之間頻率比將保持不變，行人相位在每個周期會以固定角度(相對橋梁運動)滑移。對于橋梁較大振幅情況(圖4(b))，行人相對橋梁的相位滑移程度在每個周期不同，當行人頻率接近橋梁頻率時，中間會經歷一個間歇不連續的過渡過程，之后，行人的步頻將會收斂于橋梁頻率，同時兩者之間有一個特定相位差，與初始相位差無關[30]。

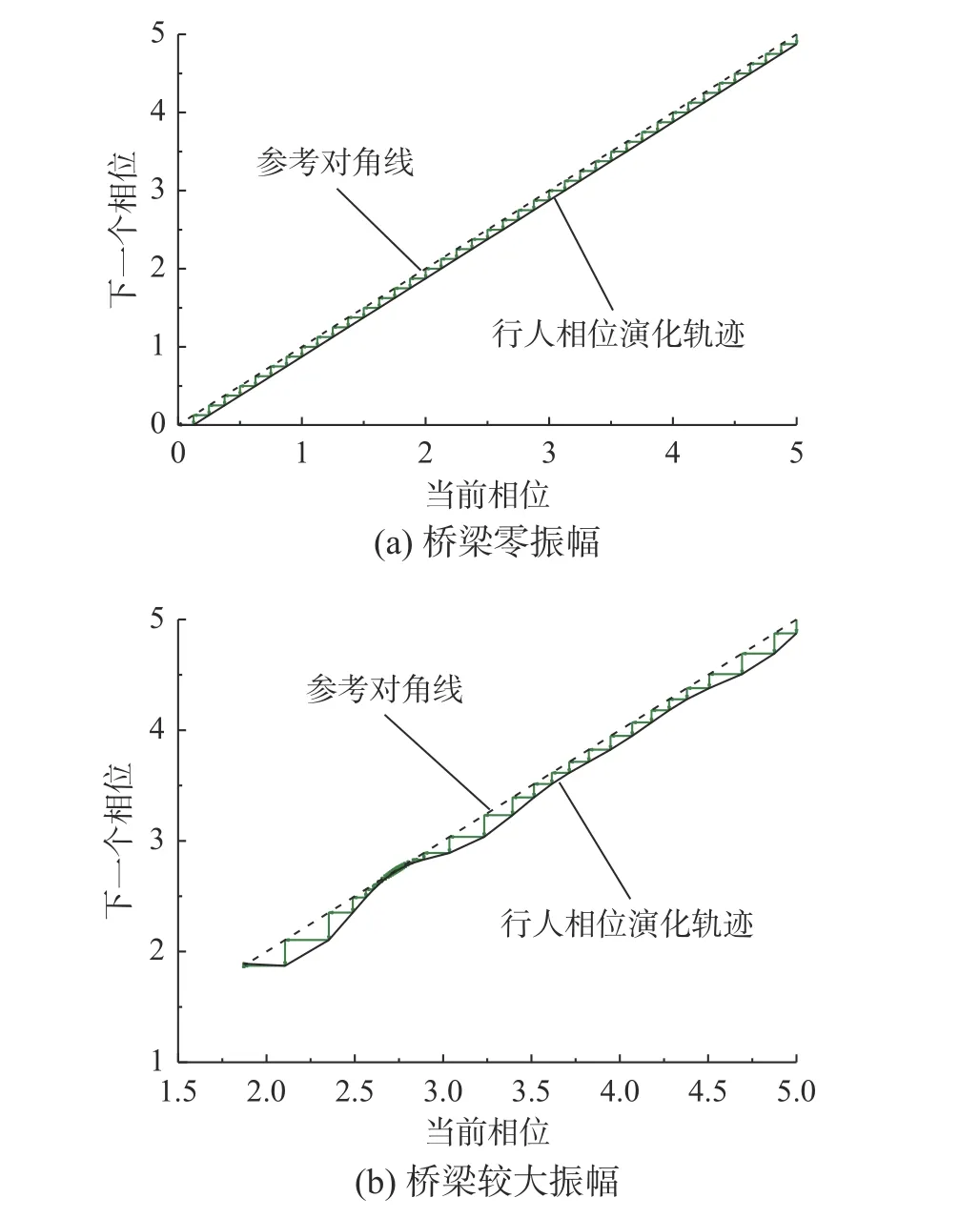
圖4 行人相位演化軌跡圖Fig. 4 Trajectory of pedestrian phase evolution

3 IP-K 模型

3.1 人-橋振動控制系統方程

首先，直接給出橋梁振動的模態方程：

3.2 人群部分同步狀態

通過下式將式(16b)轉換為旋轉坐標系中：

3.3 考慮人群部分同步的 cp修正

4 算例分析

英國倫敦千禧橋的跨徑組成為北跨81 m+中跨144 m+南跨108 m。考慮到北跨有較為完整的關于臨界人數的記錄，因此將千禧橋北跨作為分析對象。千禧橋大幅橫向振動事故發生后，Arup 公司組織人群進行了現場人致振動測試[1]，其獲得的關鍵信息有：北跨的基頻、模態質量、模態剛度、阻尼比分別為：1.03 Hz、113×103kg、4730×103kg/s2、0.006～0.008。同時在現場還觀測到，大概150 人～170 人就能引起20 mm 左右的大幅橫向振動。假設每個行人質量為75 kg，現采用上述方法對千禧橋北邊跨橫向振動進行分析。分別采用3 種模型：① Macdonald 提出的原始IPM(這里標記為IPM-1)；② McRobie 提出的IPM 長期解模型(這里標記為IPM-2)；③ 本研究所提模型(即IP-K 模型)，計算了千禧橋北邊跨的cp值。由于Macdonald[5]只給出了IPM-1 的[κ0,κ1]=[0, 0](相對速度控制規則)和[κ0,κ1]=[0, 1](絕對速度控制規則)這兩種步行規則的結果，因此這里先給出這兩種步行規則的比較結果(圖5)。本研究所提模型采用的其他主要參數設定如下：橋上行人數量Np=170；行人對橋梁振幅A的敏感系數E=12，柯西-洛倫茲分布尺度參數r=0.02(以上參數在后文不變，除非特殊聲明—如參數分析)。

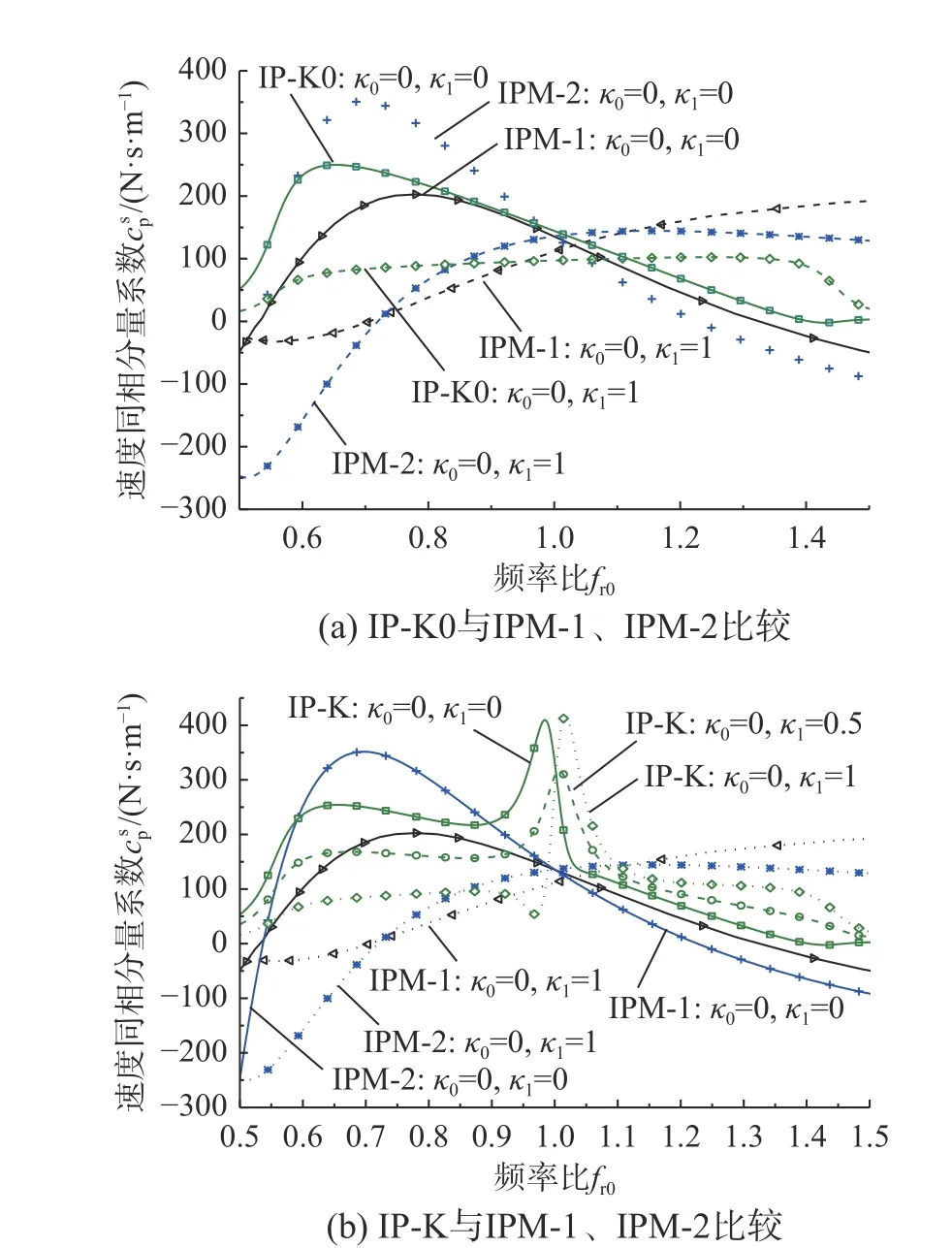
圖5 不同模型的 cp結果比較Fig. 5 Comparison of cp results of different models

首先，忽略式(44)中的一次項和二次項，只考慮常數項(即g0)對cp的貢獻，這里不妨將其稱之為IP-K0 模型。這樣處理目的在于暫不考慮橋梁振幅對行人激勵的影響(即不考慮同步效應)，但這并不意味IP-K0 模型將等同于IPM-2 相等，盡管兩者都是采用長期解模型，但必須指出的是IP-K0 模型雖然忽略了同步效應，但仍考慮了人群分布效應(行人步頻的柯西-洛倫茲分布設定)，而IPM-2 是單人模型，無法考慮人群效應(IPM-1 同樣如此)。圖5(a)給出了IP-K0 模型與IPM-1 以及IPM-2 的cp-fr0(fr0為行人步頻和橋梁橫向基頻之比的平均值)結果。總體上，三者曲線形狀及趨勢較為一致；且在fr0≈1(即行人橫向步頻接近橋梁振動頻率時，或可稱之為步頻比分布中心，為簡便，后文一律采用分布中心來指代fr0≈1位置)處附近，三者大小相差較小。盡管如此，不同模型間的cp值還是存在一定差距(尤其是IP-K0 和IPM-2)。首先，在圖中可觀測到，不同模型結果大致在分布中心處交匯，而fr0一旦稍離分布中心這個點，IP-K0 和IPM-2 的cp值差異將拉開；其次相比IPM-2，IP-K0 模型得到的結果較小，這主要是因為IP-K0 模型包含有人群分布效應(行人步頻通過概率曲線分布，每人步頻的分布區間不盡相同)，換言之，IP-K0 模型得到的是一個整體平均的結果，這間接表明了考慮人群效應的必要性。

圖5(b) 給出了本研究所提的完整IP-K 模型值(即式(44)，考慮人群分布效應以及同步效應)與IPM-1 以及IPM-2 的比較結果。從圖中可知，當[κ0,κ1]=[0,0]，IPM-2 在較低步頻的區域(并非行人正常步頻區域，行人正常步頻為fp≈0.9～1.1, 橋梁結構振動頻率為fs=1.03，fr0≈1 兩側附近區域才是行人正常步頻區域)具有較高的cp值，而在行人正常步頻區域卻偏低，遠遠小于實橋測試得到的值，IPM-1 同樣有這個現象，而這正是IPM 模型被詬病的所在，因為用非行人正常步頻區域的cp去分析橋梁振動臨界條件是不合理的。McRobie在其文中指出[29]：“Bocian[24]為了維護IPM-1 的合理性，提出在密集人群中行人可能減慢步頻，可能低至0.6 Hz，以獲得較高的cp值。然而，這和新加坡樟宜機場的測試結果相矛盾[31,37]：樟宜機場測試得到的cp值較高，而現場照片表明人群密度低，在相關的頻率圖中也沒有證據顯示行人步頻有較大異常的減低。此外，認為密集人群會降低步伐的觀點與IPM-1 支持者認為的行人步頻總是很快因而無法與結構低頻模式同步的觀點相矛盾。這說明不應該忽視某些同步的可能性，而IPM模型完全忽視人群同步現象對橋梁大幅橫向振動的潛在影響的設定并不一定合理”。從圖中可以看出，本研究所提的考慮同步效應的IP-K 模型結果為一波峰形曲線，盡管在較低步頻的區域(fr0≈0.7 附近)IP-K 模型的cp值仍然低于IPM-2 結果，但在分布中心區域，IP-K 模型的cp值卻大幅提高，接近400，明顯高于IPM-2 結果。顯然，這個結果更合理，也更接近實測結果(圖1)，有力證明了考慮同步效應的合理性。

當[κ0,κ1]=[0, 1]時，在fr0＜1 區域(圖5(b)的左側區域)，IPM 模型(IPM-2 和IPM-1)的cp很小，且大部分出現負cp值(相當于行人施加了正阻尼作用，進一步抑制振動)，而到了fr0＞1 區域(圖5(b)的右側區域)，cp值有所上升，但都偏少，離實測值較遠。而IP-K 模型cp結果仍然為一波峰形曲線，在分布中心附近出現較大的峰值cp值，雖然在左側區域也都較低，但沒有出現負cp值的情況。

5 參數分析

5.1 步行控制規則參數κ0、κ1的影響

從[κ0,κ1]=[0, 0]和[κ0,κ1]=[0,1]這兩種行人步行控制規則的對比結果中可知，這兩者結果存在一定相似性，但也存在著較大差異性。在左側區域，[κ0,κ1]=[0,0]的cp值明顯大于[κ0,κ1]=[0,1]的結果，而在右側區域，前者卻小于后者。Macdonald在提出IPM-1 模型時[5]，曾指出實際的行人步行控制規則應該介于相對速度控制規則和絕對速度控制規則之間，即：[κ0,κ1]的實際合理值應該在[0,0]和[0,1]之間。不過在IPM-1 模型中，沒有引入κ0、κ1的量化參數，只能給出相對速度控制規則(即[κ0,κ1]=[0,0])和絕對速度控制規則([κ0,κ1]=[0,1])這兩種極端情況下的結果。后來McRobie[29]引入了κ0、κ1這兩個量化參數，并分析了κ0∈[-1, 1]和κ1∈[-1, 1]多種組合工況的結果。在圖5(b)中，額外增加了一組IP-K 模型在[κ0,κ1]=[0,0.5]規則下的結果。從圖中可看出：首先，[κ0,κ1]=[0,0.5]的結果介于[κ0,κ1]=[0,0]和[κ0,κ1]=[0,1]之間；其次，[κ0,κ1]=[0,0.5]的cp峰值有所下降，但其峰值仍然高達320，與現場千禧橋的實測值基本一致(圖1)，且位于行人正常步頻區域； 還有， 相比[κ0,κ1]=[0,0]和[κ0,κ1]=[0,1]，[κ0,κ1]=[0,0.5]峰值處的頻率更接近fr0≈1。

為進一步研究κ0、κ1取值對IP-K 模型cp的影響，選取了κ0、κ1分別取0、0.5、1 時的8 種組合(圖6(a))；同時選取[κ0=0∶0.2∶1,κ1=0.5] (圖6(b))、[κ0=0.5,κ1= 0∶0.2∶1] (圖6(c))10 種κ1和κ0分別固定時的組合工況。各種工況的cp結果示于圖6，可知：

1) 首先，組合[κ0,κ1]=[1,1]的結果看上去是最不合理的，這意味著在行人步行控制規則中完全包含橋梁振動位移和橋梁振動速度是不合理的。

2) 其次，在圖6(a)中觀測到，κ1不超過0.5時，cp值在低頻段(左側)一般高于高頻段(右側)，峰值一般位于低頻段，而當κ1為1 的結果則相反。這意味著κ1取較大值時會改變曲線趨勢，產生不合理的結果，因此κ1值不應取太大。

3) 再有，考慮κ1固定為0 的情況，可以發現，在步頻中間大部分區域，κ1=0 的三條曲線大致平行，且cp隨著κ0的增大而減少。類似的，考慮κ1固定為1 的三種組合情況，在除了左、右兩端的步頻中間大部分區域，三種組合下的cp曲線大致平行，且cp隨著κ0的增大而減少，這說明在步頻中間區域，cp值和κ0呈一定的遞減線性關系(這一現象在圖6(b)的κ1=0.5 固定組合工況結果中顯得更為清楚)。

4) 在圖6(a)中和圖6(c)中可知，當κ0固定，不同κ1值的曲線間則不存在這種平行關系，它們會交叉與同一個點，間接說明cp與κ1之間存在較強的非線性關系。

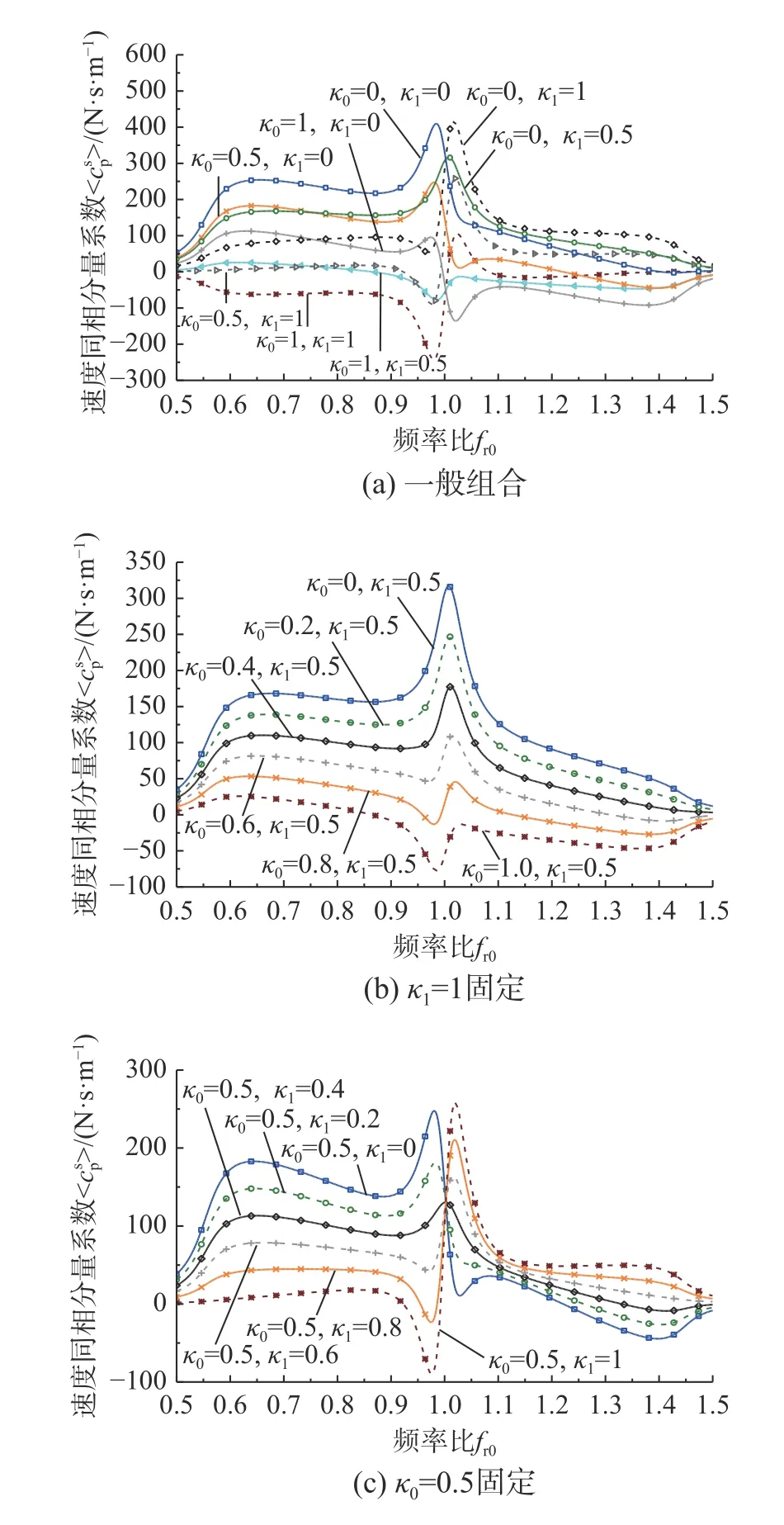
圖6 IP-K 模型在不同κ0、κ1參數組合下的 cp結果Fig. 6 cp results of IP-K model under different combinations of parameters κ0 andκ1

5) 從圖6(a)、圖6(b)、圖6(c)中，可知κ0、κ1取值對曲線峰值位置具有不同的影響。可以觀測到，當κ1取值為0 時，峰值對應的頻率比位于分布中心的左側，而當κ1取值為1 時的峰值對應的頻率比位于分布中心的右側，當κ1取值為0.5 的峰值對應的頻率比位置介于κ1=0 和κ1=1 這兩種結果的中間；而固定κ1，改變κ0對峰值位置分布并不產生影響(圖6(b)的結果尤為清楚)。綜上，可知κ0會對cp值產生影響，但這種影響是“線性”影響：隨著κ0變化，曲線會整體上升或下降，對改變曲線整體形狀的改變影響很小；而κ1除了會對cp值產生影響，對曲線峰值位置的改變也具有重要影響。

由上述分析可知，κ0和κ1取較大值會偏離實際，參考McRobie 的做法，采取一種折中的方式，同時綜合圖6 的結果，這里將[κ0,κ1]=[0,0.5]視為一組較為合理的值，并將其應用于后續分析中。

5.2 行人人數 Np的影響

5.3 柯西-洛倫茲分布中尺度參數r的影響

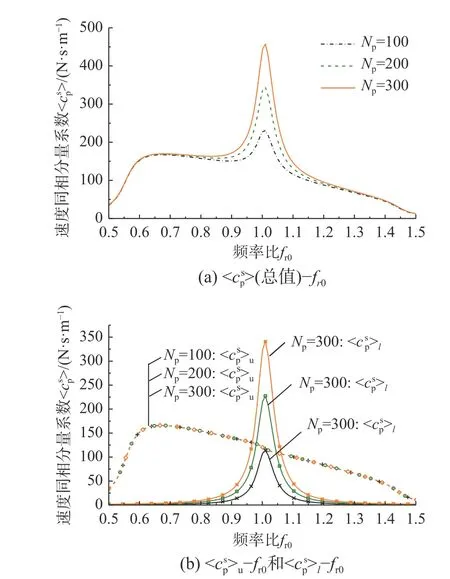
圖7 不同 Np下的〈〉-fr0Fig. 7 〈〉-fr0 under different Np values

5.4 行人對橋梁振幅的敏感系數 E的影響

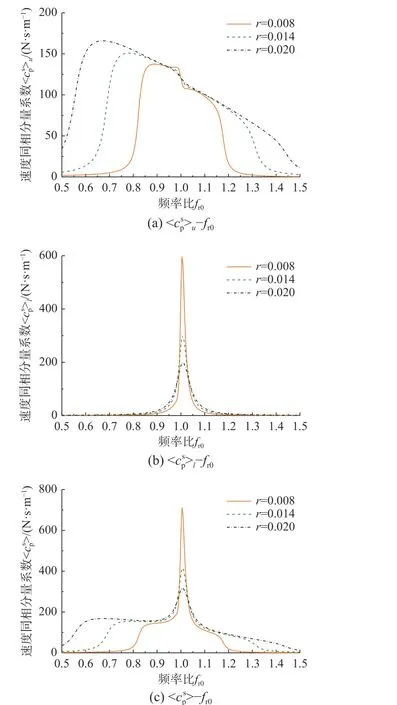
圖8 不同下的〈-fr0Fig. 8 〈〉-fr0 under different r’s

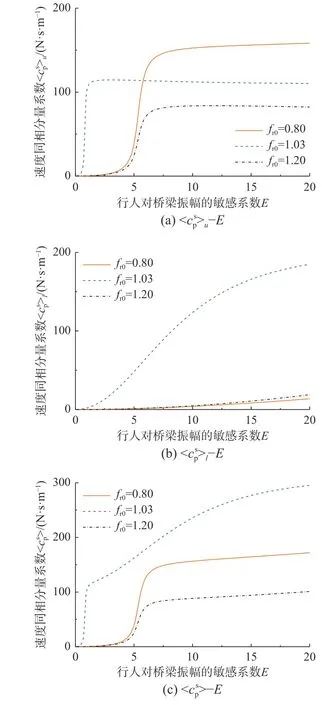
圖9 不同 fr0下的〈csp〉-E曲線Fig. 9 〈csp〉-E under different fr0’s

5.5 參數耦合分析

6 振動穩定分析

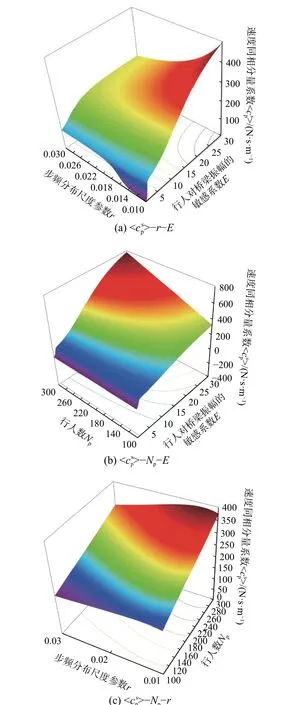
圖10 不同參數組合下的三維結果Fig. 10 3D results with different parameter combinations

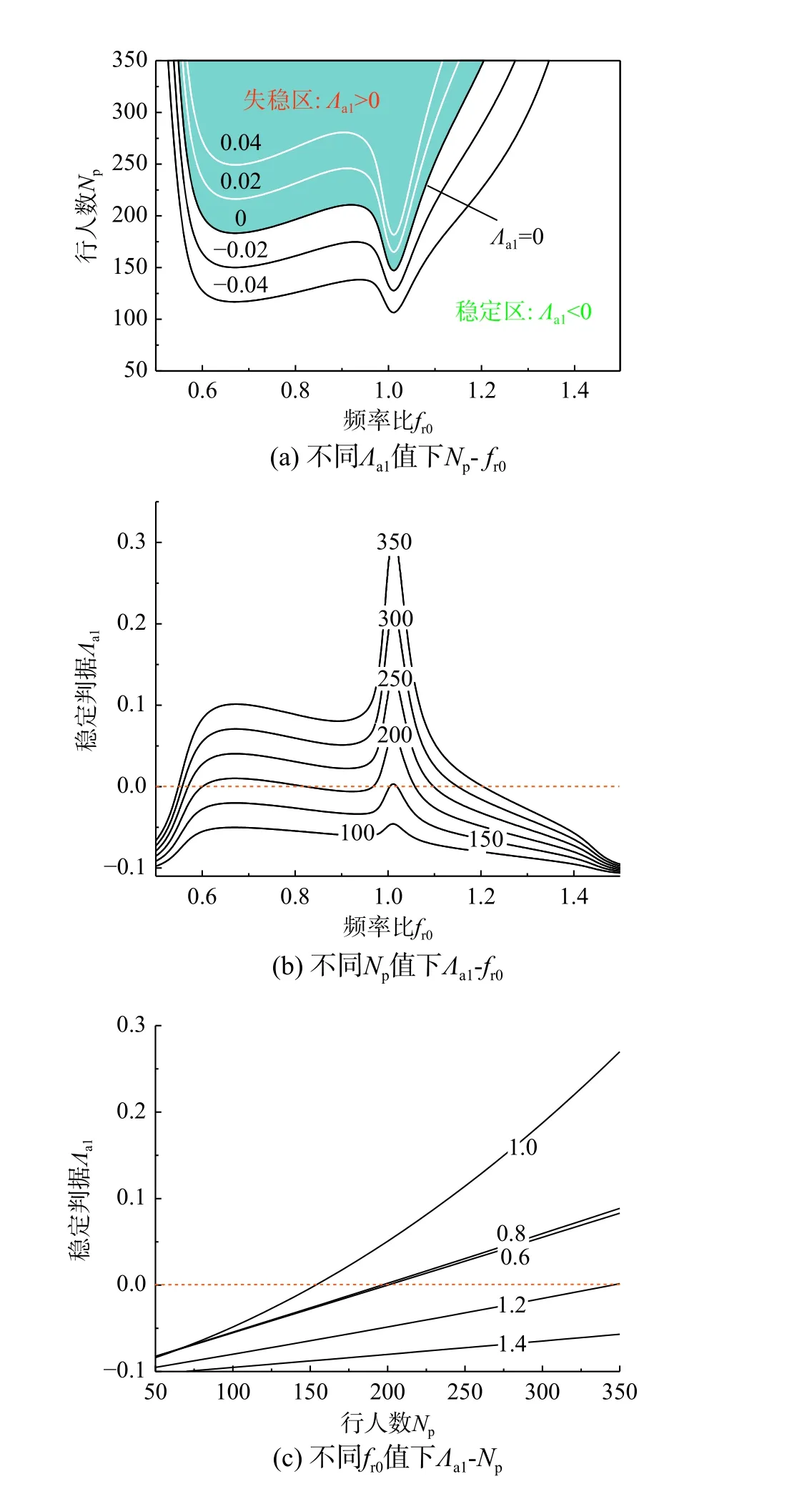
圖11 Λa1 、 Np 、 fr0不同組合等勢線圖Fig. 11 Contours of Λa1 , Np andfr0

7 結論

傳統IPM 模型沒有考慮人-橋梁之間的同步效應，得到的對應于正常步頻的速度同相自激力分量系數cp小于實測值。針對這個問題，本研究提出了一種新型人行橋人致橫向振動模型：IP-K 模型。在所提模型中，首先，橋上行人激勵模型以IPM 作為核心基礎，并考慮IPM 長期效應以便得到解析解；其次，為了彌補IPM 缺少對同步效應考慮的缺陷，引入Kuramoto 生物同步模型考慮行人-橋梁之間的同步效應。同時，所提模型采用柯西-洛倫茲分布來模擬人群中的行人步頻分布，將IPM 適用對象從單個行人擴展至人群，并基于此考慮了人群和橋梁之間同步效應引起的影響。采用所提的方法分析了千禧橋北跨的人致橫向大幅振動問題。所提模型得到cp結果和現場測試結果吻合，驗證了本研究所提方法的有效性。在本研究中得到的主要結論有：

1)原始IPM 模型只有在非行人正常步頻區域才能取得較高的cp，相比之下，經修正后得到的IP-K 模型可以在正常步頻區域獲得和現場實測結果一致的較高cp值，有力說明了考慮人群和橋梁之間同步效應的必要性。

2)行人步行控制規則的設定對以IPM 為基礎的模型影響很大，在IP-K 模型的參數分析中可知：[κ0,κ1]的實際合理值應該在[0,0]和[0,1]之間，同時κ1值不應取太大；cp值和κ0整體上呈遞減線性關系κ0變化，曲線會整體上升或下降，對改變cp曲線整體形狀的改變影響很小)，而cp與κ1之間存在較強的非線性關系(κ1除了會對cp值產生影響，對曲線峰值位置的改變也具有重要影響)；[κ0,κ1]=[0,0.5]是IP-K 模型較為理想的選擇。

3)通過對行人人數Np、柯西-洛倫茲分布中尺度參數r、以及行人對橋梁振幅的敏感系數E的參數分析，可知：IP-K 模型的〈csp〉值在分布中心兩側附近隨著Np的增加而增加，但在其他的低頻和高頻區域，Np對cp總值影響甚微；r的改變會影響〈csp〉的分布和大小，尤其會影響分布中心區域的〈csp〉峰值大小，顯示了人群同步效應對橋梁振動不可忽視的重要影響；E和〈csp〉的關系存在突變現象，兩者關系總體上可以分為兩個階段：首先是前期的緩慢增長階段，而后是快速增長階段，最后是相對平滑增長階段；Np、r和E存在不同程度的耦合效應，其中r和E的耦合效應較為明顯。

4)fr0的分布位置對穩定判斷Λa1有著重要影響，fr0分布的最不利位置在fr0≈1.01 處，fr0對Λa1的影響也和人數Np相關， Λa1對fr0的敏感度隨著Np的增大而明顯增大。

雖然目前已有不少學者開展了關于結構人致振動(包括橋梁、房屋人致振動)問題的研究，并在近期取得了不少成果[9,10,13,28,38-45]，但由于該問題的復雜性，人們對其中深藏的機理仍缺乏足夠的認識，本文所提模型將有助于揭示其中部分機理，并為后續研究提供一個思路。在所提模型中，大部分參數具有通用性，如人的橋梁振幅敏感系數和行人腳步行進規則參數κ0和κ1(這些屬于人體生物本能特性)以及柯西-洛倫茲分布的尺度參數r(雖然和不同區域種族有關，但從整體層面上看，還是可以假設其變異性不大)，而只有個別參數和實際橋梁結構相關，如行人步頻和橋梁頻率的頻率比fr0。然而，由于目前研究工作側重點在于理論模型的提出，尚未展開現場實橋試驗，人的橋梁振幅敏感系數、柯西-洛倫茲分布的尺度參數目前是按一般情況設定，其精確值還需將來實驗數據的進一步驗證核實。除了這個局限，本文所提模型并未考慮IPM 模型中產生的加速度同相分量(即忽略了系數 ρ)以及人-人同步鎖定效應。針對這些局限性問題(尤其是基于實橋試驗結果的驗證工作)，將來將展開重點研究，進一步改進和提高所提模型的性能。