兩周期激勵下Duffing-van der Pol振子的復雜簇發振蕩及其機理

張真真，馬新東

(1.江蘇大學京江學院，212013，江蘇，鎮江；2.江蘇大學土木工程與力學學院，212013，江蘇，鎮江)

0 引言

多時間尺度耦合現象廣泛存在于各種動力系統中，如物理系統中的van der Pol-Duffing系統[1]、生態系統的獵食者-食餌模型[2]、電路系統的BVP振蕩器[3]和神經系統的細胞簇放電系統[4]等。多時間尺度的耦合效應往往使系統的動力學特性表現為大幅振動和小幅振動的耦合，這種有趣的動力學行為稱為簇發，也可以叫做混合模式振蕩或張弛振蕩。大幅振動通常指的是系統軌跡在大振幅極限環內的運動，這種運動也稱為激發態，小幅振動指的是軌跡在平衡點或小振幅極限環的運動，這樣的運動稱為沉寂態。連接激發態和沉寂態的可以是分岔[5]，也可以是其他引起吸引子轉遷的路徑，如脈沖爆炸(pulse-shaped explosion)[6]等。對于連接方式為分岔的情況，Izhikevich[7]給出了光滑系統與余維-1分岔相關的幾乎所有簇發類型，并提出了一種基于分岔的簇發分類方法。

在簇發動力學研究中，由快慢變化頻率耦合誘發的簇發行為得到了人們的廣泛關注。如時培明等[8]研究了低頻參數周期激勵下旋轉機械系統的簇發行為，并給出了快變參激和慢變參激分別對簇發現象的影響規律。孟盼等[9]利用穩定性和分岔理論探討了低頻正弦激勵下前包欽格呼吸神經元系統的“Hopf/Hopf”型簇發振蕩現象。吳丹和丁旺才[10]分析了一類干摩擦碰撞系統在低頻外激勵下的簇發振蕩現象及其機理。最近，韓修靜等[11]報道了一種由2個低頻激勵耦合的滯后翻轉引起的復雜簇發行為，并給出了一種基于莫夫爾公式的相稱激勵頻率分析方法。在此方法基礎上，Zhou等[12]研究了2個慢參數激勵下的最小化學反應系統的4種復雜簇發模式及其快慢分析。Yu等[13]給出了兩低頻周期激勵下復雜機械系統的由多S形流形(multiple-S-shaped)誘發的簇發振蕩現象及其產生機制。由于2個激勵頻率之間存在不同的耦合關系，會使系統出現更為復雜的動力學行為，因此，非常有必要對2個周期激勵下的復雜簇發行為及其產生機制進行更為深入的研究。

本文考慮一類兩周期激勵下的Duffing-van der Pol系統[14]，該系統可以用于描述一個特定的非線性自激電路或一個在非線性粘性介質中運動的擺的動力學特性，數學表示式為

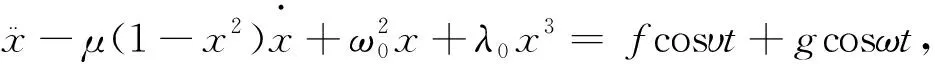
(1)

其中fcosυt和gcosωt表示2個低頻外激勵，頻率滿足0<υ<ω<<1，u是滿足某些混沌動力學特性增加的控制項。由于0<υ<ω<<1，在周期T時間內，fcosυt和gcosωt都變化緩慢，按照快慢分析法，可以令cosυt=δ、cosωt=γ，那么方程(1)轉化為廣義自治方程如下

(2)

本文旨在揭示兩周期激勵下由滯后翻轉引起的復雜簇發行為。本文組織結構如下：在第1節中，分析了單個周期激勵下系統的穩定性和分岔及其臨界條件；第2節中給出了單個激勵下的復合式delayed subHopf/fold-cycle簇發及其產生機理；借助改進型快慢分析方法；第3節研究了2個激勵下滯后翻轉型復合式delayed subHopf/fold-cycle簇發；最后，總結全文。

1 單個周期激勵下的系統穩定性和分岔分析

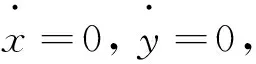
(3)

另一方面，將系統在平衡點E處線性化，可以得到雅克比矩陣

(4)

固定參數f=4，υ=0.01，λ0=1，ω0=1，μ=1，系統關于δ=cos0.01t的分岔圖如圖1所示。在區域(δLPC2,δLPC1)中，存在一個穩定的極限環LC1。在區域(δH2,δH1)中，平衡點E是不穩定的。當參數δ穿越亞臨界Hopf分岔點H1和H2后，在左右兩側出現2個穩定的平衡點E+和E-，同時出現2個不穩定的極限環LC2和LC3。通過數值模擬發現，LC2和LC3的振動幅值逐漸增大。因此區域(δH1,δLPC1)和(δLPC2,δH2)是雙穩態區域，同時存在一個穩定的極限環和一個穩定的平衡點。隨著δ穿越極限環的fold分岔LPC1和LPC2時，LC2和LC3與LC1碰撞消失，在LPC1右側和LPC2左側只剩下2個穩定的平衡點E+和E-。

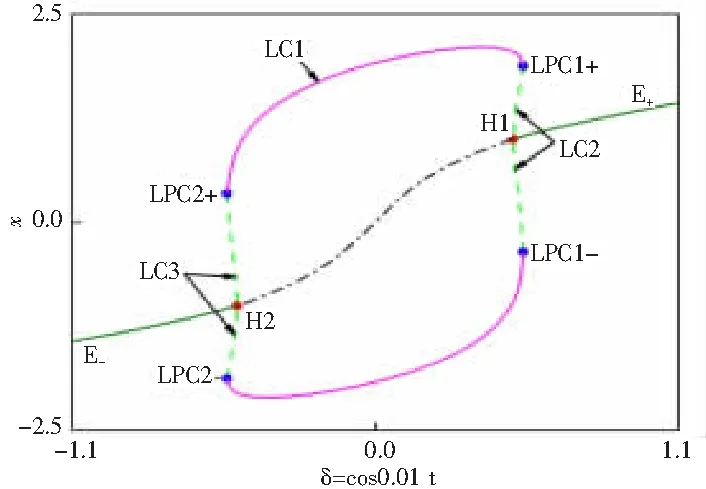
圖1 系統的穩定性和分岔

2 復合式delayed subHopf/fold-cycle簇發振蕩

這部分分析單個激勵下的復合式subHopf/fold cycle簇發行為。圖2給出了系統在(x,y)平面的相圖和時間歷程圖。顯然，從圖中可以看到這種簇發模式是關于穩定平衡點E±和穩定極限環LC1的。

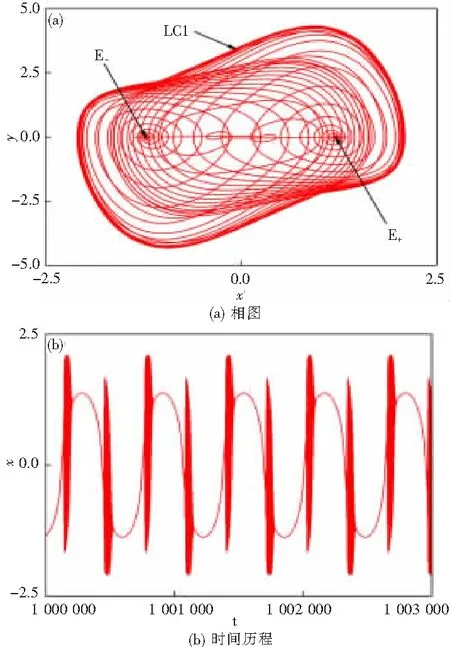
圖2 復合式delayed subHopf/fold-cycle簇發振蕩

這種簇發行為的產生機理可以通過將(δ,x)上的慢流形疊加到分岔圖上進行揭示，如圖3所示。假設軌跡在δ的最大值1處開始運動，此時系統的穩定吸引子為E+，軌跡在E+的向量場內做平滑的沉寂態運動。當δ減小到亞臨界Hopf分岔點δH1處，E+失穩，變成不穩定的平衡點。但軌跡并未立即轉到穩定極限環LC1運動，而是繼續沿著不穩定平衡點運動，直到亞臨界Hopf分岔滯后點(delayed H1)出現，軌跡才進入LC1中做大幅激發態運動。當δ變化到亞臨界Hopf分岔點δH2時，穩定平衡點E-出現，同時產生一個不穩定的極限環LC3(見圖1)。隨著δ繼續減小至極限環的fold分岔點δLPC2，LC1與圖1中的不穩定極限環LC3碰撞消失，軌跡轉而進入E-的向量場中做沉寂態運動，直至δ減小至其最小值-1。然后δ開始增大，這個過程與上面類似。

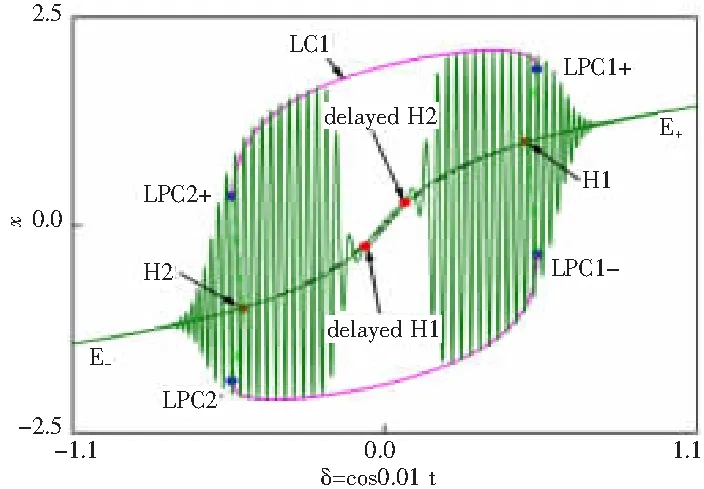
圖3 (δ,x)上的慢流形與分岔圖的疊加

從圖3可以看出，在一個周期簇發內存在2個激發態，第1個開始于亞臨界Hopf分岔滯后(delayed subHopf)，結束于極限環的fold分岔。第2個同樣開始于亞臨界Hopf分岔滯后，結束于極限環的fold分岔。按照Izhikevich[7]的分類方式，這種簇發可以命名為復合式delayed subHopf/fold-cycle簇發。

3 激勵gcosωt對復合式delayed subHopf/fold-cycle簇發的影響

上節揭示了單個激勵下的復合式delayed subHopf/fold-cycle簇發的產生機制。這部分研究另一個激勵gcosωt對這種簇發模式的影響。

3.1 研究方法

對于2個激勵下的系統動力學行為研究，可以采用韓等[14]提出的改進型快慢分析方法。這里只討論ω=nυ，n為正整數的情況。這樣方程(2)就可以轉化為含一個慢變量的二維方程(5)，如下：

(5)

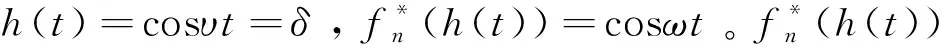
(6)

獲得，其中m是不大于n的最大偶數，i是虛數單位。

3.2 滯后翻轉型復合式delayed subHopf/fold-cycle簇發

下面研究當n取不同值時，ω對復合式delayed subHopf/fold-cycle簇發的影響。固定參數g=3，其他參數取值與圖1相同。圖4給出了n分別取1、2、3、4時的(δ,x)平面上的慢流形與分岔圖的疊加。

(a)n=1; (b)n=2; (c)n=3; (d)n=4

從圖4可以看出系統的動力學行為一直都與穩定的平衡點和穩定的極限環有關，軌跡在這2種吸引子之間通過亞臨界Hopf分岔和極限環的fold分岔相互切換。當n=1時，2個激勵與單個激勵相比，可以發現2個Hopf分岔滯后點之間的距離逐漸靠近，但仍然表現為復合式delayed subHopf/fold cycle簇發。當n=2時，第3個亞臨界Hopf分岔點H3和第2個穩定極限環LC5出現，由于分岔滯后的影響，系統的動力學行為沒有受到這2種分岔的影響，但系統主要的動力學行為右移，從圖4(b)可以看出，此時系統仍是復合式delayed subHopf/fold-cycle簇發。當n=3時，亞臨界Hopf分岔的數目又減到2，2個Hopf分岔滯后點之間的距離增大，系統激發態運動占據了主要地位，此時系統行為還是表現為復合式delayed subHopf/fold-cycle簇發。當n=4時，亞臨界Hopf分岔的數目變為5，并且在一個簇發周期內出現了4個激發態運動，每一個激發態運動都是以Hopf分岔滯后開始，以極限環的fold分岔結束，這種簇發其實是2個復合式delayed subHopf/fold-cycle簇發的組合。同時可以看到n=4時的動力學行為其實是n=2和n=3時的動力學行為的耦合，隨著n的增大，亞臨界Hopf分岔的數目將會繼續增加，n=2和n=3時的動力學行為的耦合數目也增加。同時在一個簇發周期內，復合式delayed subHopf/fold-cycle簇發的數目也越來越多，這種現象的本質是平衡滯回曲線的扭曲造成的，因此將這種復合的復合式簇發稱為滯后翻轉型復合式delayed subHopf/fold-cycle簇發。

4 結論

本文研究了2個周期激勵下Duffing-van der Pol系統的復雜簇發行為。當2個周期激勵頻率與系統固有頻率存在量級差異時，可以將周期激勵看做慢變參數，原來的非自治系統轉化為廣義自治系統。首先給出了單個激勵典型參數下的復合式delayed subHopf/fold-cycle簇發及其機理。然后研究了2個激勵頻率之間存在整數倍的滯后翻轉型復合式delayed subHopf/fold-cycle簇發。研究發現，當n取較大值時，系統的動力學行為可以表現為n取較小值時動力學行為的耦合。