基于特征空間法的美國南部大平原蒸散發遙感反演

涂晨雨，官云蘭，陳遠芳

(東華理工大學測繪工程學院，330013，南昌)

0 引言

蒸散發(Evapotranspiration，ET)是指植被及地面向大氣輸送的水汽總通量，其過程需要消耗約60%的降水和地表凈輻射，是維持全球陸-氣水分和能量平衡的關鍵要素[1]。作為地表水分循環的主要組成部分，準確估算蒸散發對于農業灌溉與干旱監測、水資源管理、氣候變化預估等研究至關重要，在水文學、生態學、氣象學和農學等諸多領域備受關注[2]。

傳統蒸散發估算方法以“點”的觀測資料為基礎，如水量平衡法、渦動相關法和大型蒸滲儀法等[3]。這些方法雖然觀測精度較高，然而對于區域尺度而言，適用性卻較差，不僅無法充分反映地表空間異質性，同時過于依賴地面數據的支持，在觀測站點稀疏及資料匱乏地區應用較為困難[4]。遙感技術具有快速、周期性、宏觀等特點，其迅速發展為區域或全球尺度的蒸散發估算提供了重要的驅動數據。在過去的幾十年間，一系列基于遙感技術的蒸散發估算模型應運而生，主要分為以下三大類：經驗統計模型、地表能量平衡模型和特征空間模型[5]。其中，特征空間模型是指地表溫度、植被指數、反照率等遙感參數，在區域尺度上，構成的散點圖呈三角形或梯形，進而以插值算法獲得蒸散發[5]。該模型通常以地表溫度和植被指數組成的特征空間為主，與其他模型相較，能有效地降低蒸散發估算對地面數據的依賴，提供了一個比較直接的反演地表通量的方法，具有較好的應用前景[6]。

對上述特征空間模型研究的過程中，許多學者發現模型估算蒸散發的準確度受干濕邊界(三角形或梯形空間的上邊界和下邊界)限制。為了有效確定模型的干邊及濕邊，研究人員提出了經驗回歸法和理論計算法[7]。然而，前者受遙感數據空間尺度效應影響較大，而后者則需近地面氣象和植被輔助，兩者均有著不確定性[7]。因此，Zhu[8]等在提出的通用三角法中，將干邊的確定從區域轉化為像元尺度，同時僅需風速作為唯一輔助數據，有效地降低觀察到的干邊所涉及的主觀性和不確定性。但該方法在極端干旱條件下的空氣溫度估算及濕邊反演時，仍然受區域限制，具有經驗性。

針對該方法存在的不足，本文在Szilagyi[9]等的研究成果的基礎上，進一步給出了干濕邊界相應的理論公式。同時，本文選定美國南部大平原(SGP)為研究區，利用MODIS(Moderate Resolution Imaging Spectroradiometer)遙感數據，構建時空二維地表溫度-植被指數特征空間，實現2017年像元尺度SGP區域地表蒸散發的遙感連續估算。此外，還采用大氣輻射測量(ARM)計劃提供的站點數據對研究結果進行驗證，評估該方法的適用性，并進一步分析研究區蒸散發時空變化規律。

1 研究區概況及數據來源

1.1 研究區概況

研究區位于美國大平原南部，經度范圍為W95°18′～99°30′，緯度范圍為N34°30′～38°30′，覆蓋了約2/3的俄克拉荷馬州以及堪薩斯州部分地區。圖1展示了該地區多樣的土地覆蓋類型，其中以種植冬小麥、棉花和玉米等的農用地以及草地為主。整個研究區地勢平坦，氣候類型豐富，地表通量屬性多樣，因此被大氣輻射測量(ARM)計劃選定為第一個氣侯試驗場，擁有大量的連續測量大氣輻射的觀測站，可給予充足可靠的氣象數據，為蒸散發模型研究及驗證提供基礎[10]。

圖1 研究區土地覆蓋類型及站點分布圖

1.2 數據來源

本文使用數據包括遙感數據和氣象站點數據。遙感數據主要來自于搭載在EOS-AM(上午軌道)和PM(下午軌道)系列衛星上的傳感器MODIS。目前為止，共有44個MODIS數據產品發布，本文中涉及的MODIS產品為MOD03、MOD06_L2、MOD07_L2、MOD11A1、MOD13A2和MCD43A3，時間范圍為2017年。上述產品在使用前均需通過預處理，提取研究所需有效數據，并重采樣至相同的空間分辨率1 km。其中，MOD13A2提供的歸一化植被指數(NDVI)用于估算研究區的植被覆蓋度(fc)，該產品時間分辨率為16 d，不同于其他產品(1 d)，需進一步插值處理得到日尺度數據。氣象觀測數據來自于大氣輻射測量計劃(https://www.arm.gov/)的波文比能量平衡系統(EBBR)。該系統可提供氣溫、濕度和風速等氣象數據，其中風速為模型所需唯一輔助數據。同時，該系統獲得的顯熱通量(H)、潛熱通量(LE)和地表凈輻射，將用于驗證研究過程中蒸發比(EF)、凈輻射以及蒸散發的估算值。其中蒸發比的計算公式如下：

(1)

2 研究方法

本文采用遙感蒸散發估算模型為地表溫度—植被指數特征空間，即在研究區內地表溫度(TS)和植被指數(VI)構成的散點圖，將呈三角/梯形空間，其中該空間形狀的上下邊界為干濕邊界。通過確定特征空間模型構建的關鍵參數(干邊和濕邊)，進而獲得修正溫度植被干旱指數(MTVDI)求解逐像元蒸發比，在此基礎上結合地表凈輻射數據，估算研究區蒸散發。

2.1 干濕邊求解

在水分脅迫條件下，地表溫度將受地表能量影響，干邊(TSmax)代表的是不同植被指數所對應的地表最大溫度。根據地表能量平衡原理，并參考Zhu等[8]的研究，TSmax求解見公式(2)。濕邊(TW)表示在水分飽和情況下的地表溫度，本文選擇濕球溫度(TWb)來代替，該參數估算根據Szilagyi等[9]的研究成果表達，見公式(3)。

(2)

(3)

式中：εSS和CS分別為裸土地表發射率和純裸土土壤熱通量占地表凈輻射的比例，取值為0.95和0.315；σ為Stefan-Boltzmann常數(5.67×10-8W/m2·K4)；cp為空氣定壓比熱容(1 012 J/kg·K)；γ為濕度計常數(0.066 4 kPa/℃)；Ta(K)為近地表空氣溫度，根據Zhu等[11]提出的方法由MOD07_L2和MOD06_L2產品求得；Td(K)是由MOD07_L2產品提供的露點溫度；Sd(W/m2)和εa分別表示下行太陽輻射和空氣發射率，ras表示裸土的空氣動力學阻抗，受地表粗糙度和風速等多影響；而Tdry表示在極端干旱條件下的空氣溫度，4個參數求解公式見式(4)～(9)。

(4)

(5)

(6)

(7)

式中：S0為大氣層頂的太陽常數(1 367 W/m2)；β依據Bisht and Bras的研究[12]設為0.2；Lv為蒸發潛熱，約為2.5×106J/kg；Rv是水汽的氣體常數(461 J/kg·K，)；e0(hPa)是近地表水汽壓，而太陽天頂角參數θ(rad)為MOD03產品提供。

(8)

(9)

式中：z(m)是參考高度，d(m)和z0m(m)是零平面位移高度和動量的表面粗糙度長度，對于裸土而言兩者分別為0和0.005；k是馮卡曼常數0.41；u(m/s)是在參考高度測量的風速，采用所有站點位置測量儀器高度2 m處風速的平均值代替；e*表示對應溫度的飽和水汽壓。

2.2 遙感蒸散發估算

在忽略日尺度土壤熱通量(G)的前提下，日蒸散發(ET)的估算公式如式(10)所示。

ET=Rn,day·EFday

(10)

式中：Rn,day為日尺度地表凈輻射，是在瞬時地表凈輻射(Rn)遙感反演的基礎上，根據Rivas &Cormora[13]研究結果估算；EFday為日尺度蒸發比，可用衛星過境時刻的瞬時蒸發比近似代替[14]。

蒸發比依據Jiang & Islam[15]等研究采用Priestley-Taylor方程[16]進行估算，見公式(11)。

(11)

式中：△表示飽和水汽壓隨氣溫(Ta)變化的斜率；φ是無量綱參數，反映實際空氣動力學和地表阻抗，是基于土壤濕度進行參數化獲得，不同像元對應的φi會隨著土壤水分有效性從干邊向濕邊增加由0到1.26線性變化。對于純植被而言，φ值(φcanopy)恒等于1.26。而對于純裸地的φ值(φsoil)，則需要采用能反映地表土壤濕度的修訂型溫度植被干旱指數(MTVDI)來計算。該指數為Zhu等[17]在Sandholt等[18]發現地表植被指數與土壤濕度之間存在變化關系，并據此提出的溫度植被干旱指數(TVDI)基礎上進一步改進獲得，公式如下：

(12)

(13)

(14)

式中：Tsoil為任意像元通過溫度分解求得的純裸土地表溫度；TS地表溫度由MOD11A1產品提供；fc植被覆蓋度可利用NDVI來估算，其中NDVImin和NDVImax分別設為0.05和0.86。

基于此，φsoil可表達為MTVDI的函數關系，見公式(15)，而混合像元的φ值以植被覆蓋度(fc)為權重，通過線性插值的方法求得：

φsoil=1.26[1-exp(MTVDI-1)]

(15)

φ=φsoil(1-fc)+φcanopyfc

(16)

2.3 檢驗指標

本文采用4個統計指標來對蒸散發估算結果進行精度評估，分別為相關系數(r)、絕對偏差(MAE)、均方根誤差(RMSE)和偏差(B)，公式如下：

(17)

(18)

(19)

(20)

3 結果與分析

3.1 精度驗證

地表溫度—植被指數特征空間模型主要估算的參數為蒸發比，需要地表凈輻射數據結合獲得蒸散發。因此，蒸散發估算結果的誤差來源于兩部分，一是蒸發比的估算；二是地表凈輻射的估算。本文結合站點實測數據，分別對蒸發比、地表凈輻射和蒸散發估算結果進行精度驗證。

在站點尺度上，2017年本文估算的蒸發比精度如表1所示。總體而言，蒸發比存在高估現象，平均偏差為0.05，其中在E12和E40站點處蒸發比高估顯著，偏差達到0.23，而在E32站點處偏差最小(B=0)。此外，蒸發比僅在E9、E11和E13站點存在低估，三者偏差分別為-0.14、-0.27和-0.10。各站點蒸發比估算值在0.10～0.84之間，與觀測值比較，兩者平均MAE、RMSE和r分別為0.13、0.15和0.69，在一定程度上達到了精度要求。以MAE、RMSE和r三者為蒸發比估算精度評價指標，從單個站點來看，E35站點處模型模擬效果總體而言最好(MAE=0.11、RMSE=0.14，r=0.76)，而在E11站點處模型模擬效果最差(MAE=0.16、RMSE=0.19)，但該站點的相關性卻較高(r=0.81)。

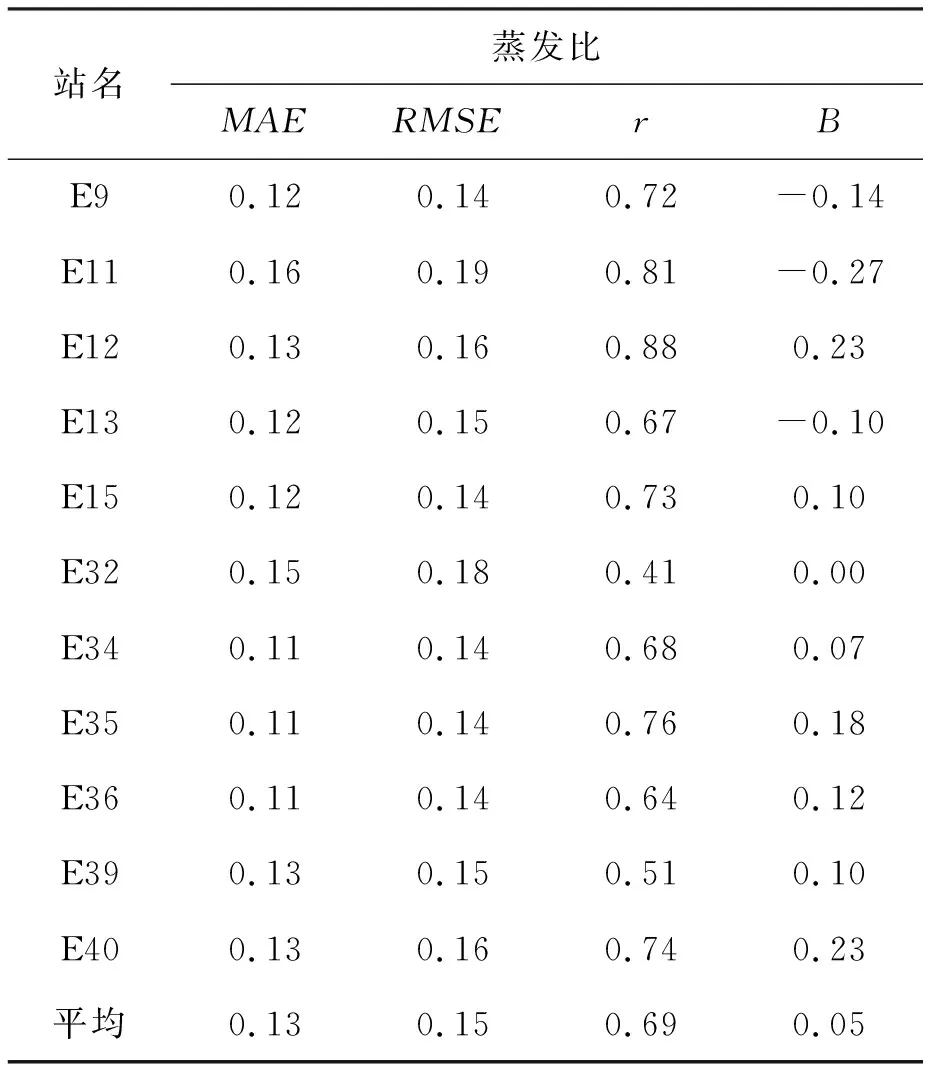
表1 各站點觀測日蒸發比與本文估算值比較

本文使用的地表凈輻射數據是參考Bisht & Bras[12]和Rivas &Cormora[13]研究結果并結合MODIS數據估算獲得。地表凈輻射估算精度如表2所示，在各站點處，凈輻射的估算結果總體略低于觀測值，平均B為-0.03。從各指標來看，凈輻射估算結果較好，總體精度較高。具體而言，凈輻射MAE范圍為19.26～24.53 W/m2，平均值21.54 W/m2，而RMSE范圍則在24.63～31.03 W/m2，平均值達到27.26 W/m2，其中在E39站點處2個值均最高，而E35站點均最低。此外，凈輻射估算值與觀測值在站點尺度具有很好的正相關性，r在0.87～0.95之間，兩者的一致性較好。

表2 各站點觀測日凈輻射與本文估算值比較

從蒸散發估算精度評價結果來看(表3)，本文蒸散發平均MAE和RMSE分別為0.82 mm和1.07 mm，平均偏差則為0.06。因此，可以說明蒸散發估算值與觀測值相比存在一定程度的高估，同蒸發比估算結果相一致。除此之外，蒸散發同樣在E11站點處模擬效果最差(MAE=1.36 mm，RMSE=1.78 mm)，而E34站點處模擬效果最好略優于E35站點。同時，結合站點尺度日蒸散比、凈輻射及蒸散發三者估算值與實測值之間的散點圖來分析(圖2)，蒸散發估算值與觀測值相關系數平均值為0.86，高于蒸發比(r=0.69)，略低于凈輻射(r=0.91)。綜合來看，本文估算的蒸散發結果與觀測值一致性較好，基本滿足精度要求，并且該結果受蒸發比估算精度影響較大，受凈輻射影響影響相對較小。

圖2 站點尺度日蒸散比、凈輻射及蒸散發三者估算值與實測值的散點圖

表3 各站點觀測日蒸散發與本文估算值比較

3.2 蒸散發時空分析

2017年，SGP研究區蒸散發為978.98 mm，月際變化如圖3所示，蒸散發變化呈顯著單峰型。其中，1—6月蒸散發持續增加，于7月達到頂峰160.74 mm，之后便逐漸下降，于12月達到低谷，蒸散發為16.09 mm。其中，4—9月溫度適宜，降水充足，為植被生長茂盛期，因而蒸發與蒸騰過程劇烈，約占全年蒸散發的79%。同時，這還與農作物種植周期有關，該地區農作物類型以冬小麥、玉米和棉花為主，冬小麥收割時段為5月下旬至6月上旬，而玉米及棉花約在9—10月采摘，從而在此之后蒸散量顯著降低。統計2017年研究區四季蒸散發總量，不同季節之間存在較大差異，春夏秋冬四季的蒸散發均值分別為251.06 mm、454.88 mm、201.54 mm和71.50 mm。其中，夏季(6—8月)蒸散發最高，占全年總量的46.46%；

圖3 2017年SGP研究區蒸散發月際變化

而春季(3—5月)蒸散發則略高于秋季(9—11月)；冬季(12—2月)蒸散發最低，僅有年蒸散發的7%。因而，夏季實際蒸散發對于年地表蒸散發總量具有較為明顯的貢獻。

通過統一空間分布圖的顯示范圍，進一步分析研究區四季蒸散發空間分布情況(圖4)。根據圖4可以看出，研究區春夏秋冬四季蒸散發西北-東南分布特征明顯，并且呈東南向西北遞減趨勢，其中蒸散發高值集中在林區，草原次之，而農業區蒸散發則最弱。由于研究區地處美國南部大平原，植被覆蓋率較高，蒸散發總量受植被蒸騰影響較大，從而兩極化相對較小。然而，考慮到受季節性氣溫、日照時長、降水量、相對濕度以及平均風速等年內分布不均的影響，研究區四季蒸散量空間分布仍具有一定差異性。對比春季和秋季蒸散發分布情況，兩季蒸散發范圍為21～300 mm，其中春季蒸散發高值區約占研究區1/5，而秋季蒸散發高值區相對較少，僅存在于東南地區。由于春季太陽輻射增強和地表溫度升高，而秋季與之相反，從而植物在春季蒸騰作用較強，進而導致春季蒸散發略高于秋季。對比夏季和冬季，兩季蒸散發差異顯著，夏季氣溫較高、降水充足，各地區蒸散發均高于200 mm，而冬季與之相反，氣溫較低，降水稀少，蒸散發均低于200 mm，并且空間分布變化也較小。

圖4 2017年SGP研究區四季蒸散發空間分布圖

4 結論

針對特征空間法干濕邊界確定時存在的主觀性和不確定性，本文結合Zhu等[8]和Szilagyi等[9]的研究成果，給出相應的干濕邊界理論公式，并利用地表溫度—植被指數特征空間法，實現2017年美國南部大平原地區日尺度蒸散發估算。同時，采用站點觀測數據對估算結果進行精度驗證，并探析該研究區蒸散發的時空分布情況。

1)在站點尺度，日蒸散發估算值與觀測值相關系數達到0.86，具有較好的一致性，兩者平均MAE和RMSE分別為0.82 mm和1.07 mm，滿足一定的精度要求。此外，本文蒸散發誤差來源于蒸發比和地表凈輻射的估算，其中蒸散發與蒸發比同觀測值相比，均存在高估，而地表凈輻射則略低于觀測值。

2)2017年研究區蒸散發為978.98 mm，從月際變化來看，蒸散發呈現為單峰型分布，7月為峰頂，12月則為低谷，蒸散發主要集中在4—9月份，與植被生長周期相一致。從季節變化來看，研究區蒸散發均呈東南高西北低的分布趨勢，并且蒸散發季節差異顯著，蒸散發大小按季節排序依次為夏季>春季>秋季>冬季。