基于隨機(jī)分塊的稀疏子空間聚類方法
張 琦,鄭伯川,張 征,周歡歡
(1.西華師范大學(xué)數(shù)學(xué)與信息學(xué)院,四川南充 637009;2.西華師范大學(xué)計(jì)算機(jī)學(xué)院,四川南充 637009)
0 引言
聚類分析是數(shù)據(jù)挖掘領(lǐng)域的關(guān)鍵技術(shù)之一,是將一群不相關(guān)的對(duì)象劃分為相似對(duì)象的過程。
在許多實(shí)際應(yīng)用中,高維數(shù)據(jù)通常漸進(jìn)地存在于低維子空間,其中每個(gè)子空間對(duì)應(yīng)一個(gè)類。子空間聚類是指將給定的取自于多個(gè)子空間并集中的數(shù)據(jù)點(diǎn)劃分到潛在子空間,在運(yùn)動(dòng)分割、圖像聚類、基因表達(dá)聚類等領(lǐng)域都有著重要應(yīng)用。
無監(jiān)督數(shù)據(jù)的存在使得子空間聚類成為高維數(shù)據(jù)分析的有力工具。常見的子空間聚類方法主要分為四類:基于代數(shù)的方法、基于迭代的方法、基于統(tǒng)計(jì)的方法、基于譜聚類(Spectral Clustering,SC)的方法。近年來,基于SC 的稀疏子空間聚類(Sparse Subspace Clustering,SSC)算法基于稀疏表示理論,通過對(duì)系數(shù)矩陣施加l
約束,獲得數(shù)據(jù)的稀疏表示,從而捕獲數(shù)據(jù)的全局結(jié)構(gòu)。SSC 一經(jīng)提出,就得到了廣泛關(guān)注和大量應(yīng)用。所謂稀疏性就是指用盡量少的原子基來表示數(shù)據(jù),即數(shù)據(jù)的非零系數(shù)的個(gè)數(shù)盡量少。近年來,研究者們?cè)赟SC 的基礎(chǔ)上進(jìn)行了不同的拓展:Liu 等提出的低秩表示(Low-Rank Representation,LRR)模型,通過對(duì)數(shù)據(jù)施加低秩約束來獲取低秩表示,從而捕獲數(shù)據(jù)的全局結(jié)構(gòu);低秩SSC(Low-Rank SSC,LRSSC)將SSC 與LRR 相結(jié)合,不僅對(duì)系數(shù)進(jìn)行稀疏約束,同時(shí)在模型中加入低秩約束,結(jié)合了稀疏性與低秩性的優(yōu)點(diǎn);結(jié)構(gòu)化的SSC(Structured SSC,SSSC)將每個(gè)數(shù)據(jù)點(diǎn)表示為其他數(shù)據(jù)點(diǎn)的結(jié)構(gòu)化稀疏線性組合,設(shè)計(jì)了一個(gè)統(tǒng)一的優(yōu)化框架,可以同時(shí)學(xué)習(xí)親和矩陣和子空間的分割;為了解決SSC 時(shí)間復(fù)雜度與問題大小的立方成正比問題以及SSC 不處理未用于構(gòu)造相似度圖的樣本外數(shù)據(jù),可擴(kuò)展的SSC 采用“采樣―聚類-編碼-分類”策略來解決可擴(kuò)展性和樣本外問題;內(nèi)核SSC(Kernel SSC,KSSC)利用核技巧,將SSC 擴(kuò)展到非線性流形,在高維特征空間中利用非線性解析表示實(shí)現(xiàn)了更好的聚類;魯棒子空間聚類(Robust Subspace Clustering,RSC)提出了一種兩步l
最小化算法,利用泛函分析的思想,解決噪聲數(shù)據(jù)的聚類問題;迭代重加權(quán)的SSC(Reweighted SSC,RSSC)算法,相對(duì)于傳統(tǒng)的l
最小化框架,不僅提高了算法性能,而且更加逼近l
最小化框架;基于正交匹配追蹤的SSC(scalable SSC by Orthogonal Matching Pursuit,SSCOMP)在廣義條件下既提高了計(jì)算效率,又保證了保持子空間的親和性;基于自表達(dá)和集群效應(yīng)的算法,利用集群效應(yīng)進(jìn)行自表達(dá),并且使用l
范數(shù)誘導(dǎo)稀疏,解決了SSC 中關(guān)聯(lián)矩陣過于稀疏時(shí)忽略同一子空間數(shù)據(jù)的相似結(jié)構(gòu)問題;基于低秩轉(zhuǎn)換的SSC(SSC with Low-Rank Transformation,SSC-LRT)算法提出了一種結(jié)合低秩轉(zhuǎn)換與SSC 相結(jié)合的兩階段迭代策略,解決了非獨(dú)立假設(shè)下的聚類問題、隨機(jī)SSC(Stochastic SSC via Orthogonal Matching Pursuit with Consensus,SCOMP-C)引入Dropout,解決了子空間聚類中的過度分割問題,提升了親和圖的連通性。在SSC 方法中,如果數(shù)據(jù)集中數(shù)據(jù)點(diǎn)個(gè)數(shù)少,稀疏系數(shù)矩陣相對(duì)更容易求解,因此本文提出隨機(jī)分塊的SSC 方法,將原問題數(shù)據(jù)分成幾個(gè)數(shù)據(jù)量更少的問題求解。該方法的創(chuàng)新主要包括:
1)將原問題隨機(jī)劃分為T
個(gè)子問題進(jìn)行求解,將T
個(gè)子問題的稀疏系數(shù)矩陣進(jìn)行組合,然后采用SC 算法實(shí)現(xiàn)原問題的聚類;2)提出了一種隨機(jī)分塊策略與擴(kuò)充策略,利用該策略實(shí)現(xiàn)多個(gè)子問題分解和多個(gè)子問題系數(shù)矩陣的組合。
1 稀疏子空間聚類
稀疏子空間聚類主要包括兩個(gè)階段:1)使用稀疏或低秩最小化約束從數(shù)據(jù)中學(xué)習(xí)相似度矩陣;2)利用SC 對(duì)相似度矩陣進(jìn)行分割。SC 是否成功很大程度上取決于構(gòu)建一個(gè)信息豐富的相似度矩陣。
稀疏子空間聚類是一種基于自表示的方法。基本思想是:來自d
維子空間S
中的任意數(shù)據(jù)點(diǎn)y
都可以被表示成來自子空間S
的其他數(shù)據(jù)點(diǎn)的一個(gè)線性組合。其中,因此,理想情況下,一個(gè)數(shù)據(jù)點(diǎn)的稀疏表示中非零系數(shù)的個(gè)數(shù)對(duì)應(yīng)于潛在子空間的維數(shù)。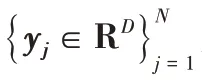


c
的解,最小化目標(biāo)函數(shù)為:
l
范數(shù)是非凸優(yōu)化問題和NP 難的,可用l
范數(shù)來凸松弛l
范數(shù),原問題可轉(zhuǎn)化為l
最小化問題:
矩陣形式的公式為:
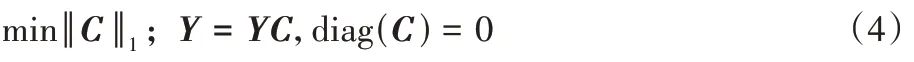

考慮到噪聲和離群值:
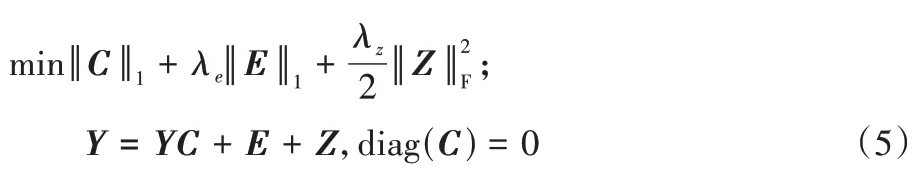
E
∈R表示離群點(diǎn),Z
∈R表示噪聲;λ
、λ
是平衡參數(shù),用于平衡目標(biāo)函數(shù)的三個(gè)項(xiàng)。在一些實(shí)際問題中,數(shù)據(jù)位于仿射子空間而非線性子空間的并集。因此,為了將位于仿射子空間并集中的數(shù)據(jù)點(diǎn)進(jìn)行聚類,稀疏優(yōu)化方程進(jìn)一步改進(jìn)為:
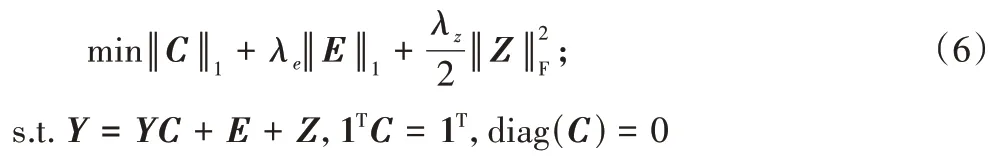
Z
:
A
∈R,加入?yún)?shù)λ
,以及2個(gè)懲罰項(xiàng),得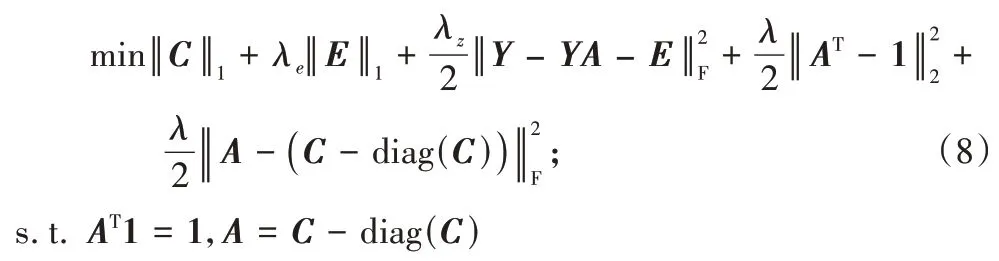
δ
∈R,Δ
∈R,得到式(6)的拉格朗日函數(shù):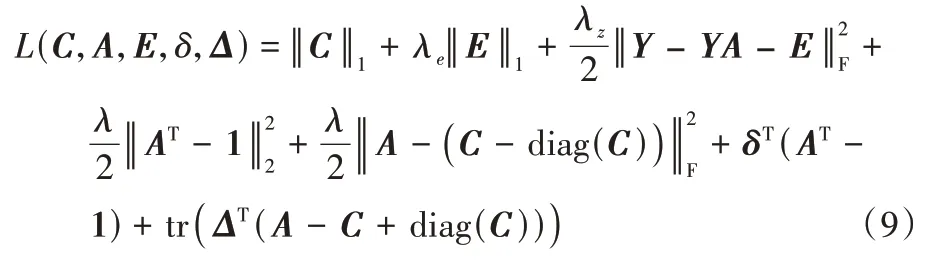
通過交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)求解式(9),可以獲得系數(shù)矩陣,則相似度矩陣定義為:

W
輸入到SC 算法,即可獲得最終聚類結(jié)果。SSC 的框架如圖1 所示。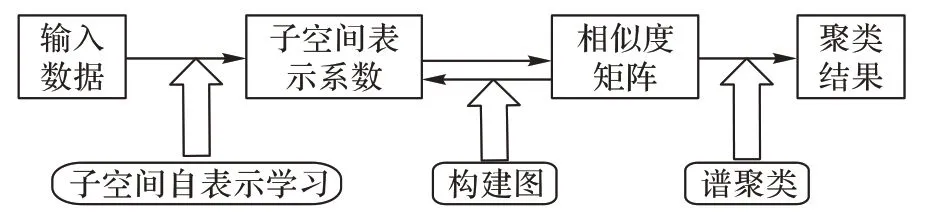
圖1 SSC框架Fig.1 Framework of SSC
SC 借助圖論的知識(shí),將所有數(shù)據(jù)點(diǎn)看作空間中的點(diǎn),點(diǎn)與點(diǎn)之間用邊相連,兩點(diǎn)之間的距離越遠(yuǎn),邊的權(quán)重越小,反之越大。通過對(duì)所有數(shù)據(jù)點(diǎn)組成的圖進(jìn)行分割,使得不同子圖之間邊的權(quán)重盡可能低,子圖內(nèi)邊的權(quán)重盡可能高,從而達(dá)到聚類的目的。將式(10)作為相似圖中點(diǎn)之間的權(quán)值矩陣,那么可以利用SC 來對(duì)稀疏子空間進(jìn)行聚類。
算法1 SC 算法。
輸入 相似度矩陣W
。輸出 數(shù)據(jù)集Y
的k
子集劃分y
,y
,…,y
。步驟1 計(jì)算相似矩陣W
的拉普拉斯矩陣L
: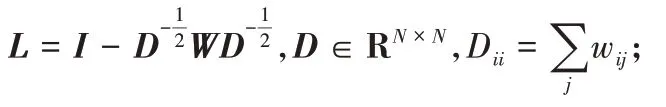
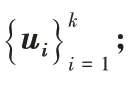
k
個(gè)n
維特征向量列成n
×k
的矩陣;步驟4 把生成的矩陣每一行看作k
維空間的一個(gè)向量,使用K-
Means 聚成k
類。2 基于隨機(jī)分塊的稀疏子空間聚類
2.1 算法思想和聚類求解框架
在深度網(wǎng)絡(luò)的訓(xùn)練過程中,Dropout 技術(shù)將神經(jīng)網(wǎng)絡(luò)中的每個(gè)神經(jīng)元按照一定的概率使其暫時(shí)在神經(jīng)網(wǎng)絡(luò)中失效。通過每次隨機(jī)地使某些神經(jīng)元失效,減少神經(jīng)元之間的相互作用,使得網(wǎng)絡(luò)模型不依賴于某些局部神經(jīng)元,從而減輕過擬合現(xiàn)象。
受神經(jīng)網(wǎng)絡(luò)中使用的Dropout 的啟發(fā),本文提出在稀疏子空間稀疏系數(shù)矩陣求解過程中引入隨機(jī)分塊策略,將數(shù)據(jù)集隨機(jī)劃分成幾個(gè)子集,每個(gè)子集作為一個(gè)子問題分別求解出系數(shù)矩陣C
,然后將所有子問題的系數(shù)矩陣通過擴(kuò)充后累加成一個(gè)相似矩陣W
,進(jìn)而進(jìn)行SC。基于隨機(jī)分塊的SSC 的框架如圖2 所示。
圖2 基于隨機(jī)分塊的SSC框架Fig.2 Framework of SSC based on random blocking
2.2 數(shù)學(xué)模型
基于隨機(jī)分塊的SSC 將原問題轉(zhuǎn)換為T
個(gè)子問題,每個(gè)子問題的目標(biāo)函數(shù)可以采取以下形式:
Y
表示第t
(t
=0,1,2,…,T
)個(gè)子問題的數(shù)據(jù)集的矩陣形式;C
表示第t
個(gè)子問題的系數(shù)矩陣。在現(xiàn)實(shí)世界中,大多數(shù)是噪聲數(shù)據(jù)集,所以子問題目標(biāo)函數(shù)采用以下形式:
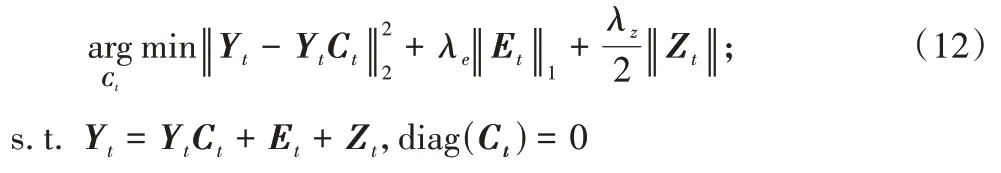
E
表示第t
個(gè)子問題的離群點(diǎn);Z
表示第t
個(gè)子問題的噪聲。2.3 隨機(jī)分塊策略
基于隨機(jī)分塊的SSC 將原問題的數(shù)據(jù)集劃分成幾個(gè)子集分別求解稀疏系數(shù)矩陣。對(duì)原問題的數(shù)據(jù)集的劃分采用如下的隨機(jī)分塊策略進(jìn)行:
設(shè)idx
是1 到N
的N
個(gè)數(shù)構(gòu)成的隨機(jī)序列,idx
是指標(biāo)集,表示每個(gè)數(shù)據(jù)點(diǎn)在數(shù)據(jù)集Y
中所處的列指標(biāo);設(shè)k
是每次從數(shù)據(jù)集中選擇的數(shù)據(jù)比例數(shù)。隨機(jī)分塊策略是每次從指標(biāo)集idx
中選擇連續(xù)的k
*N
個(gè)數(shù)據(jù)構(gòu)成一個(gè)指標(biāo)集子集,然后根據(jù)指標(biāo)集子集從數(shù)據(jù)集中獲得子問題的子數(shù)據(jù)集。隨機(jī)分塊策略具體操作如下: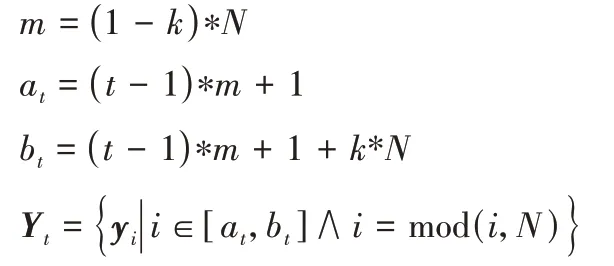
m
表示每次前進(jìn)的步長;Y
表示第t
個(gè)子問題的數(shù)據(jù)集;a
表示子集Y
的指標(biāo)集的開始位置;b
表示子集Y
的指標(biāo)集的結(jié)束位置;函數(shù)mod(i
,N
)是求余函數(shù)。2.4 子問題系數(shù)矩陣的擴(kuò)充策略
求得每個(gè)子問題的系數(shù)矩陣后,需要將T
個(gè)子問題的系數(shù)矩陣進(jìn)行整合。首先將每個(gè)子問題的(k
*N
)*(k
*N
)維系數(shù)矩陣C
擴(kuò)充為N
*N
維的系數(shù)矩陣C′
;然后將子問題系數(shù)矩陣進(jìn)行疊加得到C′′
;最后,將疊加后的系數(shù)矩陣的每個(gè)單元值除以該單元對(duì)應(yīng)的兩個(gè)數(shù)據(jù)點(diǎn)被同時(shí)分配相同子集的次數(shù),從而得到最終的系數(shù)矩陣C
。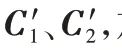
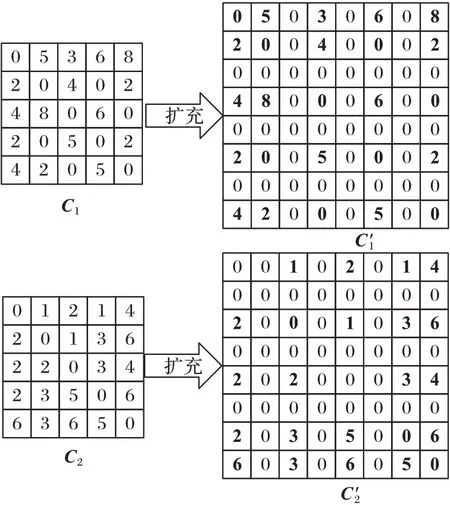
圖3 系數(shù)矩陣的擴(kuò)充Fig.3 Expansion of coefficient matrix
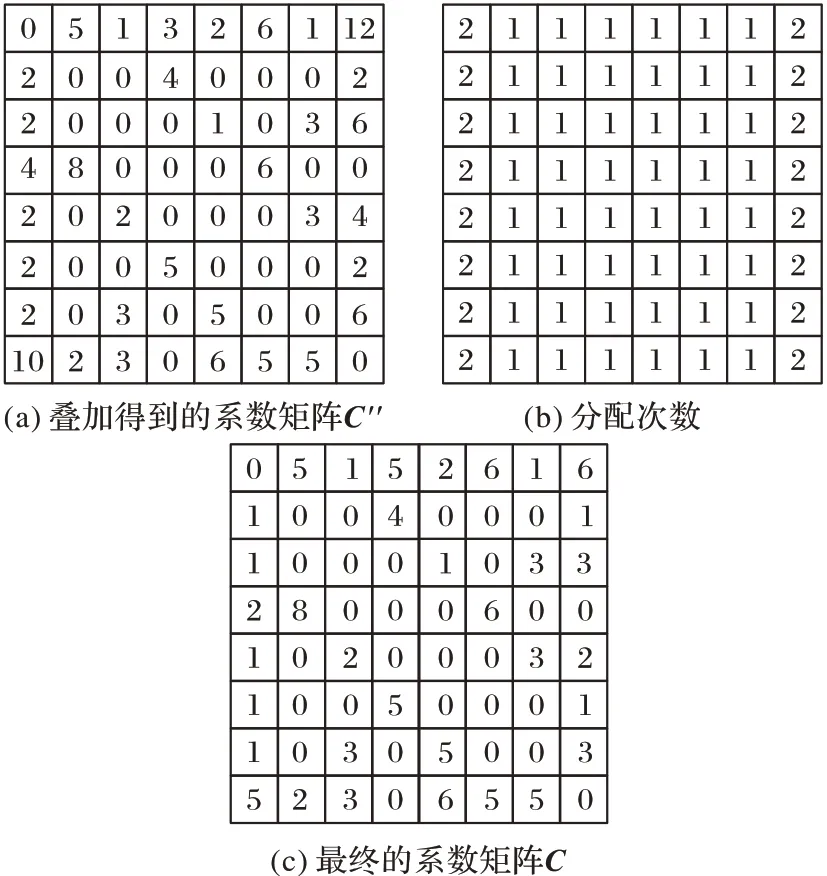
圖4 系數(shù)矩陣整合Fig.4 Coefficient matrix integration
2.5 交替方向乘子算法求解子問題
使用交替方向乘子法(ADMM)可以求解拉格朗日函數(shù)式(9)的最小值,從而求得系數(shù)矩陣C
。算法2 交替方向乘子算法。
輸入 數(shù)據(jù)集Y
。輸出 系數(shù)矩陣C
。步驟1 設(shè)置參數(shù):
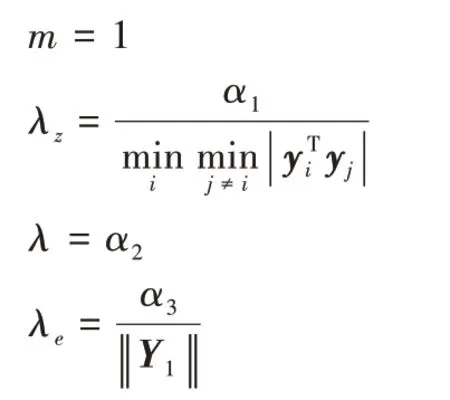
i
=0,A
=0,C
=0,δ
=0,E
=0,Δ
=0步驟3 重復(fù)以下步驟直到算法收斂或迭代達(dá)到最大次數(shù):
步驟3.1 固定(C
),E
),δ
),Δ
)),通過更新A
極小化L
: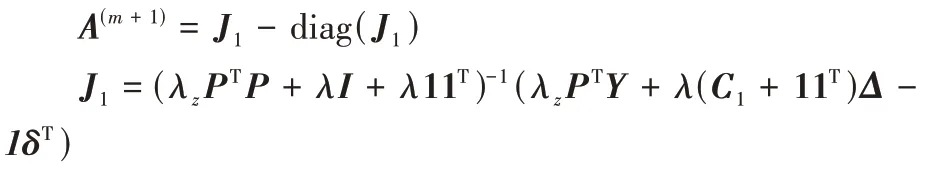
P
=[Y
,I
/λ
],C
=[C
;λE
]步驟3.2 固定(A
),E
),δ
),Δ
)),通過極小化L
更新C
: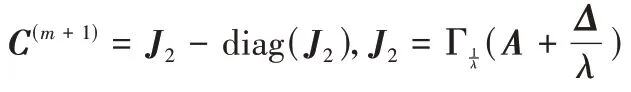
v
|-η
,0)*sign(v
)步驟3.3 固定(A
),C
),δ
),Δ
)),通過極小化L
更新E
: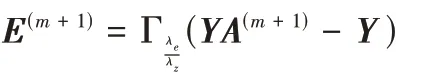
C
),E
),A
)),更新(δ
,Δ
):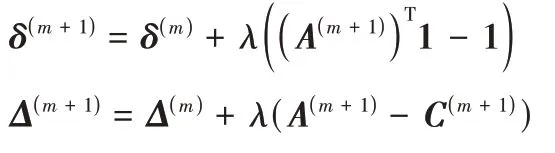
m
=m
+12.6 完整算法
式(12)的求解分兩階段迭代進(jìn)行:第一階段,對(duì)數(shù)據(jù)集進(jìn)行2.2 節(jié)中的隨機(jī)分塊操作,將原問題轉(zhuǎn)化為T
個(gè)子問題;第二階段,根據(jù)SSC 算法求出當(dāng)前子問題的系數(shù)矩陣,然后將T
個(gè)系數(shù)矩陣進(jìn)行根據(jù)2.4 節(jié)的擴(kuò)充策略進(jìn)行整合,最后對(duì)整合后的系數(shù)矩陣進(jìn)行聚類。具體算法如下:算法3 基于隨機(jī)分塊的SSC。
輸入D
×N
的矩陣Y
,參數(shù)m
,α
,α
,α
,k
,T
。輸出 聚類結(jié)果。
步驟1 將原數(shù)據(jù)按照2.3 節(jié)的隨機(jī)分塊策略隨機(jī)劃分成T
個(gè)子集Y
,Y
,…,Y
,從而將原問題劃分為T
個(gè)子問題;步驟2.1 針對(duì)每個(gè)子問題的數(shù)據(jù)矩陣Y
,執(zhí)行算法2,獲得每個(gè)子問題的系數(shù)矩陣C
;步驟2.2 將每個(gè)子問題的系數(shù)矩陣C
按照2.4 節(jié)的擴(kuò)充策略,擴(kuò)充成N
×N
維的系數(shù)矩陣C
′;步驟3 將T
個(gè)系數(shù)矩陣C
′進(jìn)行疊加,疊加之后,每個(gè)單元值除以該單元對(duì)應(yīng)的兩個(gè)數(shù)據(jù)點(diǎn)被同時(shí)分配相同子集的次數(shù),從而得到原問題的系數(shù)矩陣C
;步驟4 采用式(10)構(gòu)建相似矩陣W
;步驟5 采用算法1,進(jìn)行SC。
3 實(shí)驗(yàn)與結(jié)果分析
實(shí)驗(yàn)中,針對(duì)不同的聚類目標(biāo)數(shù)量,首先,對(duì)不同的選點(diǎn)比例和子空間數(shù)進(jìn)行實(shí)驗(yàn),探究選點(diǎn)比例與子空間數(shù)對(duì)聚類誤差的影響;然后選擇最優(yōu)的選點(diǎn)比例與子空間數(shù),將本文提出的方法與稀疏子空間聚類(SSC)、隨機(jī)稀疏子空間聚類(SCOMP-C)、基于正交匹配追蹤的稀疏子空間聚類(SSCOMP)、譜聚類(SC)和K
均值(K
-Means)進(jìn)行比較。3.1 數(shù)據(jù)集
本文使用Extended Yale B 人臉數(shù)據(jù)集進(jìn)行實(shí)驗(yàn)。Extended Yale B 數(shù)據(jù)中每張圖像的像素均為192*168,總共有38 個(gè)人,每個(gè)人有64 張?jiān)诓煌庹諚l件下的正面人臉圖像。將所有人臉圖像的大小調(diào)整為16×14,并將每張圖像轉(zhuǎn)換成一個(gè)224 維向量。因此,被聚類的每個(gè)數(shù)據(jù)點(diǎn)有224 維,屬于高維聚類問題。圖5 展示了人臉數(shù)據(jù)集中10 個(gè)人在不同光照條件下的部分圖片。

圖5 人臉數(shù)據(jù)集的部分圖片F(xiàn)ig.5 Part images in face dataset
3.2 評(píng)價(jià)指標(biāo)
為了評(píng)估聚類算法的性能,采用了4 個(gè)度量指標(biāo):子空間聚類誤差(Subspace clustering error)、互信息(Mutual information)、蘭德指數(shù)(Rand index)和熵(Entropy),它們的定義分別為式(13)~(16):

X
是數(shù)據(jù)點(diǎn)的一種劃分;Y
是數(shù)據(jù)點(diǎn)的另一個(gè)劃分;n
為數(shù)據(jù)點(diǎn)的數(shù)量;TP
為劃分正確的數(shù)據(jù)點(diǎn)數(shù)量;TN
為劃分錯(cuò)誤的數(shù)據(jù)點(diǎn)數(shù)量。子空間聚類誤差用于衡量聚類準(zhǔn)確率,聚類誤差越小越好;互信息、蘭德指數(shù)均用于衡量數(shù)據(jù)分布的吻合程度,取值范圍為[0,1],其值越大越好;熵用于衡量變量的不確定程度,值越小越好。
3.3 實(shí)驗(yàn)結(jié)果與分析
算法3 中的三個(gè)參數(shù)α
、α
、α
均設(shè)置為20,m
=150,k
表示選點(diǎn)比例,T
表示子問題數(shù)。為了探索算法針對(duì)不同目標(biāo)數(shù)的性能,實(shí)驗(yàn)分別對(duì)不同的聚類目標(biāo)數(shù):Subjects
∈{2,3,4,5,6,7}進(jìn)行實(shí)驗(yàn),此時(shí),數(shù)據(jù)矩陣Y
的大小分別為224 ×(64 ×Subjects
)。表1 展示了當(dāng)子問題中數(shù)據(jù)點(diǎn)的數(shù)量按照比例選擇時(shí),選點(diǎn)的比例與子問題的數(shù)量對(duì)實(shí)驗(yàn)結(jié)果中的聚類誤差的影響。其中,T
∈{5,6,7,8,9} 表示子問題的個(gè)數(shù),k
∈{0.7,0.75,0.8,0.85,0.9}表示選點(diǎn)的比例,黑體字表示最優(yōu)項(xiàng)。在Subjects
∈{2,3,4,5,6,7}的實(shí)驗(yàn)中,無論k
,T
取何值時(shí),效果均優(yōu)于SSC。當(dāng)k
=0.85 時(shí)的聚類誤差幾乎都小于其他選點(diǎn)比例的聚類誤差,且隨著T
的增加,聚類誤差逐漸降低,而后趨于平穩(wěn)。故本文按照k
=0.85 的比例選擇每個(gè)子問題的點(diǎn)數(shù),子問題數(shù)為T
=8。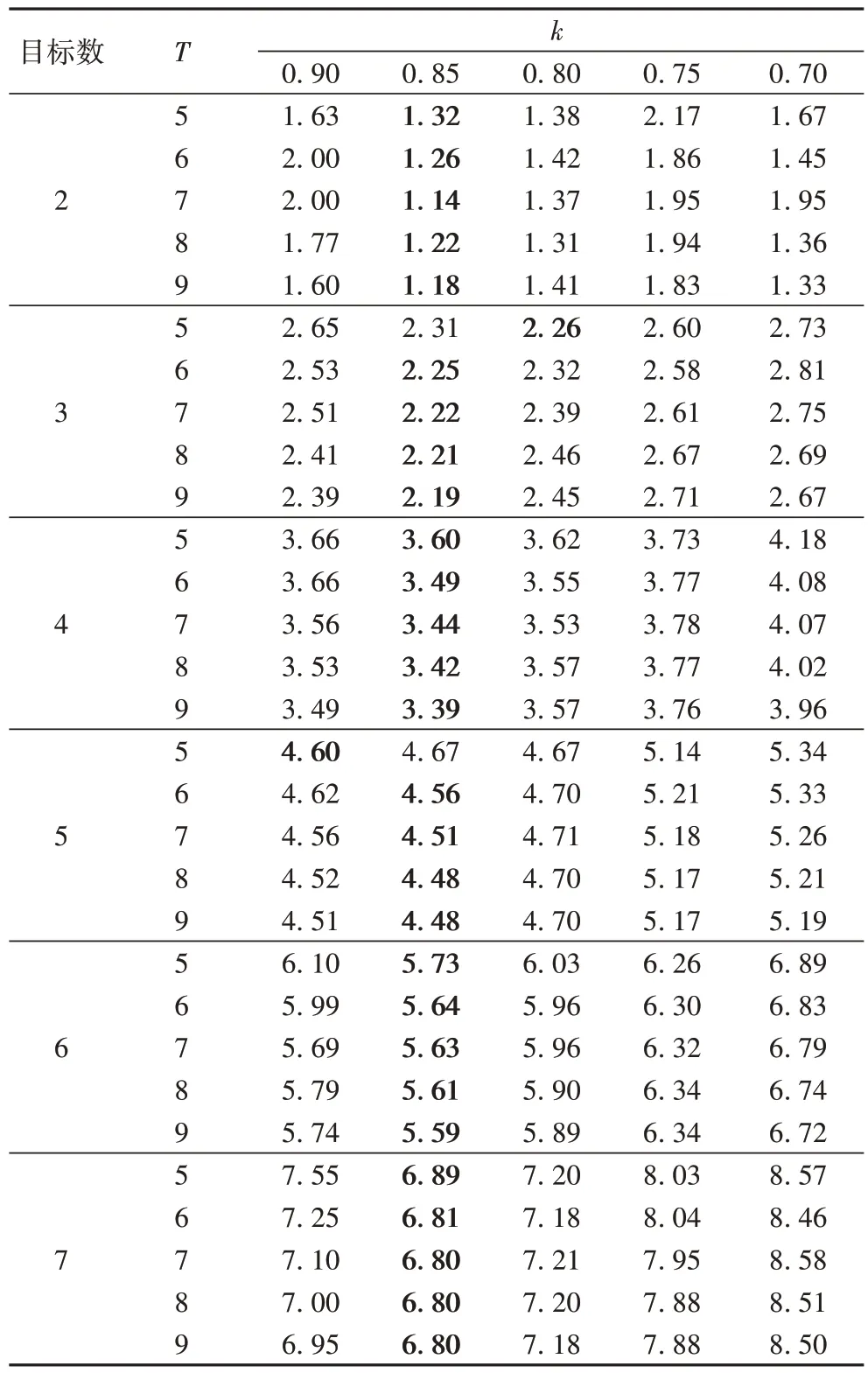
表1 子問題數(shù)與選擇數(shù)據(jù)點(diǎn)的比例對(duì)聚類誤差的影響Tab 1 Influence of ratio of number of sub-questions to selected data points on clustering error
表2 展示了當(dāng)k
=0.85,T
=8 時(shí),本文方法在人臉數(shù)據(jù)集上與SSC、SCOMP-C、SSCOMP、SC 和K
-Means 算法進(jìn)行比較的實(shí)驗(yàn)的結(jié)果,其中黑體字表示最優(yōu)項(xiàng)。可以發(fā)現(xiàn):在Subjects
∈{2,3,4,5,6,7}時(shí),本文方法的聚類誤差和熵均比其他對(duì)比方法小,而互信息和蘭德指數(shù)相較于其他對(duì)比方法大。其中,相較于5 種對(duì)比方法中的最優(yōu)方法,聚類誤差平均降低了3.12 個(gè)百分點(diǎn),熵平均降低了6 個(gè)百分點(diǎn),互信息提升4 個(gè)百分點(diǎn),蘭德指數(shù)提升2 個(gè)百分點(diǎn)。說明與其他算法相比,結(jié)合了隨機(jī)分塊策略與擴(kuò)充的SSC 算法顯著優(yōu)于其他5 種方法。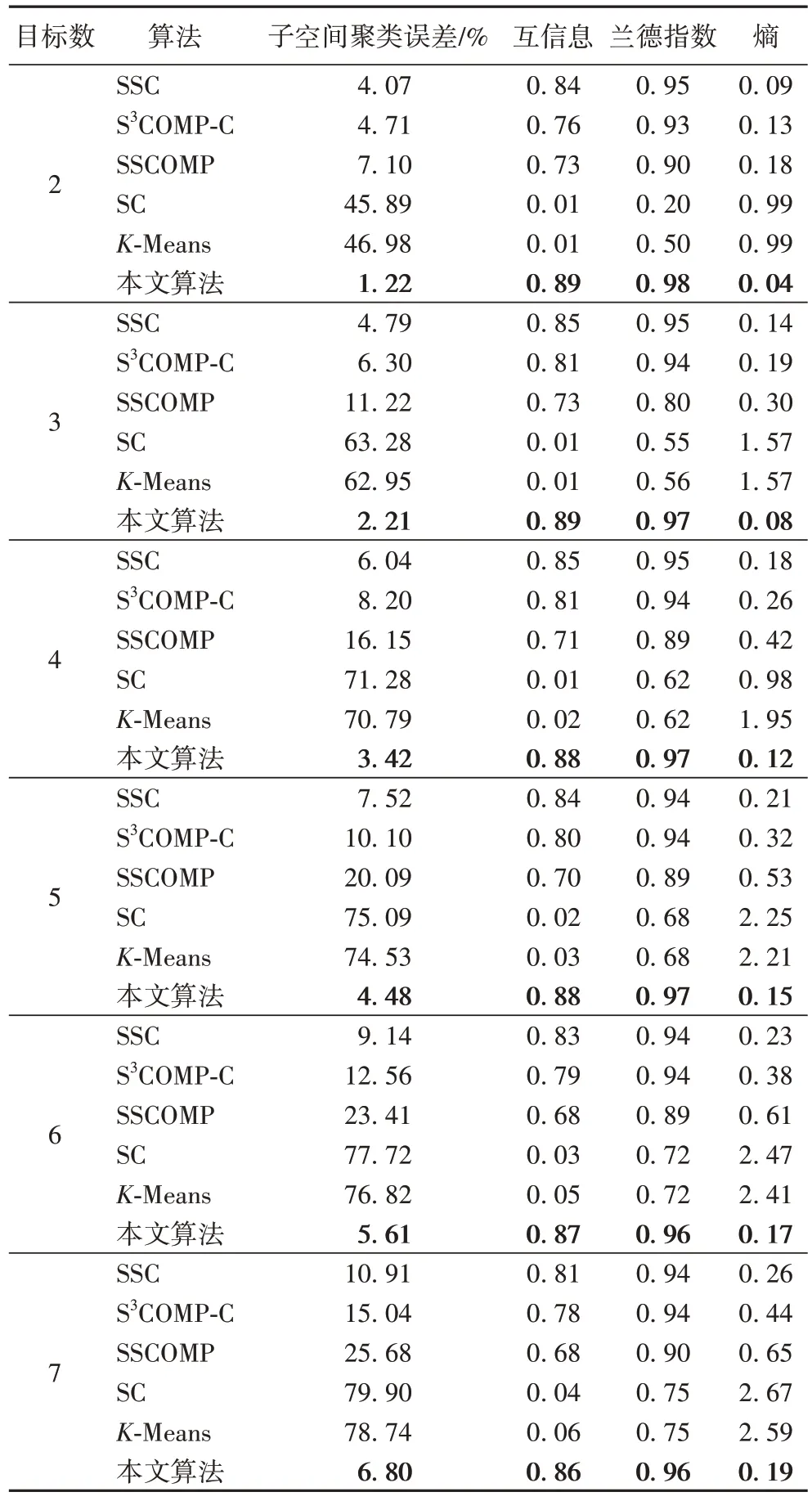
表2 Extended Yale B數(shù)據(jù)集中不同數(shù)量對(duì)象的人臉圖像的5種聚類評(píng)估(k=0.85,T=8)Tab 2 Five clustering evaluations of face images with different numbers of objects in Extended Yale B dataset(k=0.85,T=8)
4 結(jié)語
本文提出了一種基于隨機(jī)分塊的SSC 方法,每次隨機(jī)選擇固定數(shù)量的點(diǎn),將原問題轉(zhuǎn)換為T
個(gè)子問題進(jìn)行求解,將原優(yōu)化問題重新表述為一組小規(guī)模子問題上的聚類問題。還探索了選點(diǎn)比例以及子問題數(shù)對(duì)實(shí)驗(yàn)結(jié)果的影響。在人臉數(shù)據(jù)集上的實(shí)驗(yàn)結(jié)果表明,本文方法顯著優(yōu)于其他5 種方法。
