例談“概率與統計”主題的學科一般觀念
安徽 陳緒豐 祝 峰
高中數學中可以把概率與統計、三角、解析幾何、立體幾何、數列等相對獨立的數學分支視為一個學科.學科一般觀念是指對本學科學習和研究具有廣泛、持久、深刻影響的基本數學思想方法和基本思維策略.這些數學思想和思維策略是構建學科知識,利用學科知識提出問題、分析問題、解決問題的思維方向和行為策略.它們是學好本學科的基礎和關鍵,是解決本學科問題的金鑰匙.數學教學中,需要有意識地培養學生從基本概念、基本原理及其聯系出發,來思考和解決問題,持續關注學生學科一般觀念的發展.學科一般觀念的缺失或薄弱,會導致學科學習松散化、碎片化,問題解決游離化、機械化.特別是高考備考教學,其知識的回顧性、系統性與綜合性為發展學生的學科一般觀念提供了良好契機.樹立并強化學科一般觀念是提高學生應試能力的大道和王道,更是發展學生思維能力、培養學科核心素養的正道.下文結合實例,呈現概率與統計主題中包括概念觀、原理觀、符號觀、分析觀、模型觀、圖形觀在內的,六種核心學科一般觀念,旨在為概率與統計主題的高考復習提供一個全新的備考視角.
一、概率統計主題的內容要求
《普通高中數學課程標準(2017年版2020年修訂)》的課程內容設置中,必修課程和選擇性必修課程均包括概率與統計主題.
1.必修課程
必修課程中設置在主題四,包括概率、統計兩個單元.
(1) 概率單元內容包括:隨機事件的概率、隨機事件的獨立性.要求學生結合實例,理解樣本點、有限樣本空間、隨機事件,會計算古典概型中簡單隨機事件的概率,加深對隨機現象的認識和理解.
(2)統計單元內容包括:獲取數據的基本途徑及相關概念、抽樣、統計圖表、用樣本估計總體.要求學生進一步學習數據收集和整理的方法、數據直觀圖表的表示方法、數據統計特征的刻畫方法;通過具體實例,感悟在實際生活中進行科學決策的必要性和可能性;體會統計思想與確定思想的差異、歸納推理與演繹證明的差異;通過實際操作、計算機模擬等活動,積累數據分析的經驗.
2.選擇性必修課程
選擇性必修課程中設置在主題三,是必修課程中概率與統計內容的延續,包括計數原理、概率、統計三個單元.
(1)計數原理單元內容包括:兩個基本計數原理、排列組合、二項式定理.本單元可以幫助學生理解兩個基本計數原理,運用計數原理探索排列、組合、二項式定理等問題.
(2)概率單元內容包括:隨機事件的條件概率、離散型隨機變量及其分布列、正態分布.本單元的學習,可以幫助學生了解條件概率及其與獨立性的關系,能進行簡單計算;感悟離散型隨機變量及其分布列的含義,知道通過隨機變量更好地刻畫隨機現象;理解伯努利試驗,掌握二項分布,了解超幾何分布;感悟服從正態分布的隨機變量,知道連續型隨機變量;基于隨機變量及其分布解決簡單的實際問題.
(3)統計單元內容包括:成對數據的統計相關性、一元線性回歸模型、2×2 列聯表.本單元的學習,可以幫助學生了解樣本相關系數的統計含義,了解一元線性回歸模型和2×2列聯表,運用這些方法解決簡單的實際問題.會利用統計軟件進行數據分析.
二、概率統計主題的學科一般觀念1.概念觀
概念是進行邏輯判斷的基本依據,是數學思維的最小單元.“核心概念往往具有鮮明的直觀背景,簡單、易懂且威力無窮.”概率統計主題的復習備考中,應引導學生回到概念思考問題的習慣,遠離“題型+技巧”的雕蟲小技,集中注意力于核心概念,學會用概念分析和解決問題,只有這樣才能實現“減輕負擔,提高質量”的高效備考.
【例1】(2021·新高考Ⅰ卷·8)有6個相同的球,分別標有數字1,2,3,4,5,6,從中有放回的隨機取兩次,每次取1個球.甲表示事件“第一次取出的球的數字是1”,乙表示事件“第二次取出的球的數字是2”,丙表示事件“兩次取出的球的數字之和是8”,丁表示事件“兩次取出的球的數字之和是7”,則
( )
A.甲與丙相互獨立
B.甲與丁相互獨立
C.乙與丙相互獨立
D.丙與丁相互獨立
答案:B


依據相互獨立事件的概念知,只有甲與丁兩事件相互獨立,故選B.
評析:本題回歸到古典概型、排列組合、相互獨立事件的定義上.依據古典概型的定義,分別求出相關事件的概率;再由兩個隨機事件相互獨立的含義,如判斷事件之間的獨立性.判斷事件A,B是否獨立,只需先計算對應概率,再判斷P(A)·P(B)=P(AB)是否成立.
2.原理觀
概率研究的對象是隨機現象,主要是從不確定性角度認識客觀世界,并提供隨機現象研究特有的思維模式和問題解決方法; 概率為統計的學習提供理論基礎.概率與統計問題的統計思想有別于確定性思維,所用到的歸納推斷也有別于演繹證明.要求學生在學習過程中,要整體遵循不確定、隨機、歸納等一些基本的原理.
【例2】(2021·新高考Ⅰ卷·9)有一組樣本數據x1,x2,…,xn,由這組數據得到新樣本數據y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c為非零常數,則
( )
A.兩組樣本數據的樣本平均數相同
B.兩組樣本數據樣本中位數相同
C.兩組樣本數據的樣本標準差相同
D.兩組樣本數據的樣本極差相同
答案:CD
解析:對于A,E(y)=E(x+c)=E(x)+c且c≠0,故平均數不相同,錯誤;對于B,若第一組中位數為xi,則第二組的中位數為yi=xi+c,顯然不相同,錯誤;對于C,D(y)=D(x)+D(c)=D(x),故方差相同,正確;對于D,由極差的定義知,若第一組的極差為xmax-xmin,則第二組的極差為ymax-ymin=(xmax+c)-(xmin+c)=xmax-xmin,故極差相同,正確,故選CD.
評析:聚焦樣本數據的平均數、中位數、標準差、極差的概念及實際意義,考查樣本數據線性復合后,其相關數字特征之間關系的基本原理.一組樣本數據x1,x2,…,xn,由這組數據得到新樣本數據y1,y2,…,yn,其中yi=kxi+c(i=1,2,…,n),c為非零常數,則兩組數據的數字特征之間存在著關系,可依據概念予以推導.
3.符號觀
高中階段概率與統計專題的學習中,符號意識同樣關鍵,要求學生能夠理解并運用規范的符號表示事件、事件關系,以及常見的統計數據和統計模型.能夠自覺地使用符號描述隨機現象和統計規律,并借助符號進行歸納、推理和運算.
在概率與統計主題的高考備考中,樹立符號觀念,有助于學生理解概念、原理的本質.養成善于使用符號進行數學表達和數學思考的習慣,善于將冗長、煩瑣的文字描述轉換符號表達,使概率統計問題的思考、解決、表達和交流簡單、直接、明了.

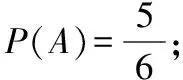
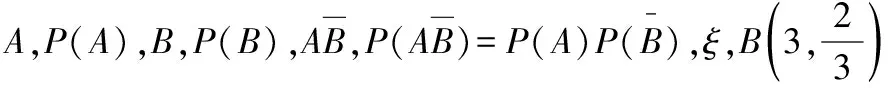
4.分析觀
包含“發現、提出、分析、解決問題”在內的“四能”課程目標中,發現和提出問題的能力在學習過程中意義突出,但應試過程中“分析問題”的能力卻尤為重要.應試中問題是現成的,并不需要發現和提出問題,合理、深入、全面的分析問題是順利解決問題的前提和保障.概率與統計主題高考備考中,分析問題有其特殊內容指向和手段,主要包括實際問題的模型化分析、隨機事件構成和關系的分析、樣本數字的特征分析、用樣本的數字特征估計整體的合理性分析等.高三備考的概率與統計主題教學中,應通過實例,訓練學生從概念原理的分析視角,豐富多措并舉的分析手段,強化確定范疇、厘清關系的分析標準,樹立分析在前、解決在后的問題分析觀.
【例4】(2021·新高考Ⅰ卷·18)某學校組織“一帶一路”知識競賽,有A,B兩類問題.每位參加比賽的同學先在兩類問題中選擇一類并從中隨機抽取一個問題回答,若回答錯誤則該同學比賽結束;若回答正確則從另一類問題中再隨機抽取一個問題回答,無論回答正確與否,該同學比賽結束.A類問題中的每個問題回答正確得20分,否則得0分;B類問題中的每個問題回答正確得80分,否則得0分.已知小明能正確回答A類問題的概率為0.8,能正確回答B類問題的概率為0.6,且能正確回答問題的概率與回答次序無關.
(1)若小明先回答A類問題,記X為小明的累計得分,求X的分布列;
(2)為使累計得分的期望最大,小明應選擇先回答哪類問題?并說明理由.
答案:B類
解析:(1)小明先回答A類問題,其答題情況共三類:①A類問題答錯,得0分,比賽結束;②A類問題答對,且B類問題答錯,得20分,比賽結束;③A類問題答對,且B類問題答對,得100分,比賽結束.上述三種情況對應事件互斥,同時注意到兩類問題能否正確回答相互獨立.所以X的取值可能為0,20,100.
P(X=0)=1-0.8=0.2;
P(X=20)=0.8×(1-0.6)=0.32;
P(X=100)=0.8×0.6=0.48.
所以X的分布列為
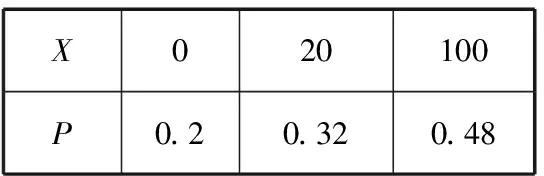
X020100P0.20.320.48
(2)由(1)知,E(X)=0×0.2+20×0.32+100×0.48=54.4.若小明先回答B問題,記Y為小明的累計得分,則Y的所有可能取值為0,80,100.
P(Y=0)=1-0.6=0.4;
P(Y=80)=0.6×(1-0.8)=0.12;
P(Y=100)=0.8×0.6=0.48,
所以E(Y)=0×0.4+80×0.12+100×0.48=57.6.
E(Y)>E(X),所以小明應選擇先回答B類問題.
評析:分析小明答題的所有情況,明確各情況的關系,是清晰準確運算出各情況所對應事件概率的前提和基礎.如第(1)問中,且B類問題答錯是答對的對立事件,A類問題答對和B類問題答錯是相互獨立事件,所以P(X=20)=0.8×(1-0.6)=0.32,復雜事件的概率求解中,應先分析事件的構成情況,明確其由哪些子事件的構成,這些子事件的關系是怎樣的,才能準確求得隨機事件的概率.
5.模型觀
在必修及選擇性必修課程的概率與統計主題學習中,有大量常見特殊的問題情境.如排列組合中的相鄰問題、不相鄰問題、局部順序確定問題、分組分堆問題、至少問題;概率中的古典概型、幾何概型、條件概率;統計中的線性回歸分析、超幾何分布、二項分布、正態分布等,可以把這些典型的問題視為特殊模型.問題解決過程中,應樹立模型觀念,在模型觀念的引領下,仔細分析問題情境,排除干擾因素,抓住關鍵,厘清本質,將具體問題歸結到確定的模型上,問題即可快速得到準確的解答.
【例5】(2021·全國乙卷理·6)將5名北京冬奧會志愿者分配到花樣滑冰、短道速滑、冰球和冰壺4個項目進行培訓,每名志愿者只分配到1個項目,每個項目至少分配1名志愿者,則不同的分配方案共有
( )
A.60種
B.120種
C.240種
D.480種
答案:C

評析:排列組合問題中“分組、分堆問題”“至少”問題.“至少”問題模型中,應先分組,即把5人分成2,1,1,1四組,再排列.
6.圖形觀
圖形觀是指借助圖形和想象,運用概率與統計的方法來感知隨機現象,利用幾何直觀理解和解決概率和統計問題的思維習慣.主要包括:借助幾何直觀認知隨機事件的關系、構成及規律;利用圖表及圖形來描述、分析概率與統計問題;建立隨機現象與幾何直觀的聯系,構建概率與統計問題的直觀模型、探索問題解決的思路.
( )
答案:B
解析:如圖,設從區間(0,1),(1,2)中隨機取出的數分別為x、y,則實驗的所有結果構成區域為Ω={(x,y)|0 評析:借助線性規劃知識,利用平面區域描述問題情境中的隨機現象.首先用不等式組描述隨機現象的樣本空間,以及事件所對應空間,再構建不等式組對應幾何直觀,幾何概型定義下,結合幾何直觀求得隨機事件的概率. 學科核心素養是學科知識、技能遺忘后,余留下來的并持續發揮作用的東西.學科一般觀念的發展,能夠有效促進核心素養的提升.“數學的本質是不斷拋棄較特殊的概念,尋求較一般的概念;拋棄特殊的方法,尋求一般的方法”.實際上,數學學習的目標不僅在于數學概念、數學定理的積累,更在于形成這些概念和定理背后蘊含的一般觀念、一般方法和學科品性.
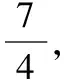
三、結語


