例談導(dǎo)數(shù)求解函數(shù)單調(diào)性的類型及策略

云南 馬孟華 趙寅輝

隨著高考改革的不斷深入，全國高考數(shù)學(xué)文、理卷(包括2021年不分文理的新高考Ⅰ，Ⅱ卷)中對導(dǎo)數(shù)的考查成為了重點(diǎn)、熱點(diǎn)問題，也是高考中區(qū)分度高、難度較大的題目.縱觀近年來高考數(shù)學(xué)中對導(dǎo)數(shù)的考查，往往以壓軸題型登場，其考點(diǎn)主要集中在以下幾個(gè)方向：(1)導(dǎo)數(shù)幾何意義的應(yīng)用(研究函數(shù)圖象的切線問題)；(2)導(dǎo)數(shù)在研究函數(shù)的單調(diào)性、極值、最值上的應(yīng)用；(3)導(dǎo)數(shù)在研究函數(shù)零點(diǎn)、方程的根問題上的應(yīng)用；(4)導(dǎo)數(shù)在研究函數(shù)不等式恒成立、有解、證明不等式成立問題上的應(yīng)用等.在上述考查方向的背景下，在函數(shù)中“引入?yún)?shù)”，就會(huì)使得問題變得更加復(fù)雜和困難，故也使問題有了較大的難度和區(qū)分度，這也是導(dǎo)數(shù)常常作為壓軸題登場的原因之一.

下面以“導(dǎo)數(shù)的應(yīng)用”為背景，從“導(dǎo)數(shù)求解函數(shù)單調(diào)性”問題的幾類模型出發(fā)，提出利用導(dǎo)數(shù)解決函數(shù)單調(diào)性的系統(tǒng)方法.旨在引領(lǐng)考生攻克高考常考考點(diǎn)及重難點(diǎn)問題，為2022年高考備考提供指引和幫助！

1.類型一：直接求解型

此類模型主要適用于函數(shù)中不含參數(shù)，且求導(dǎo)后的“導(dǎo)數(shù)不等式”可直接求解，一般這類模型問題比較簡單，如：

【例1】(2021·新高考Ⅰ卷·22(Ⅰ))已知函數(shù)f(x)=x(1-lnx).

(Ⅰ)討論f(x)的單調(diào)性.

【解析】f(x)的定義域?yàn)?0,+∞)，

又f′(x)=1-lnx-1=-lnx，

令f′(x)>0，得x∈(0,1)；

令f′(x)<0，得x∈(1,+∞).

故f(x)在(0,1)上單調(diào)遞增，在(1,+∞)上單調(diào)遞減.

【評析】對函數(shù)求導(dǎo)之后，對應(yīng)導(dǎo)函數(shù)大于(小于)0的不等式可直接求解，求出函數(shù)的單調(diào)區(qū)間，但需要注意定義域的限制.

2.類型二：“逆向”求解型

此類模型是針對函數(shù)求導(dǎo)后不等式難以“直接求解”(如：導(dǎo)函數(shù)不等式屬于超越不等式類型或?qū)Ш瘮?shù)含參數(shù))或無法求解時(shí)，可借助導(dǎo)函數(shù)的“零點(diǎn)”將函數(shù)定義域分為若干區(qū)間，在每一個(gè)區(qū)間上討論導(dǎo)函數(shù)的正負(fù)性，進(jìn)而求解出原函數(shù)的單調(diào)性.如：

【例2】已知函數(shù)f(x)=ex-ln(x+m).

(Ⅰ)設(shè)x=0是f(x)的極值點(diǎn)，求m并討論f(x)的單調(diào)性.

2.1 “逆向討論”策略

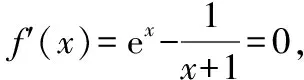
所以f(x)在(-1,0)上單調(diào)遞減，在(0,+∞)上單調(diào)遞增．

2.2 “數(shù)形結(jié)合”策略

當(dāng)x∈(-1,0)時(shí)，f′(x)<0，當(dāng)x∈(0,+∞)時(shí)，f′(x)>0，

故f(x)在(-1,0)上單調(diào)遞減，在(0,+∞)上單調(diào)遞增.

【評析】從方法二可以看到，2.1中的逆向討論法在特定情形下，也可使用數(shù)形結(jié)合的方式討論導(dǎo)函數(shù)的正負(fù)性，從而避免了分析導(dǎo)函數(shù)中各個(gè)構(gòu)成函數(shù)的正負(fù)性問題，直接從圖形上觀察得到了在定義域內(nèi)的不同區(qū)間上導(dǎo)函數(shù)正負(fù)性問題.事實(shí)上，兩類方法的理論基礎(chǔ)都建立在函數(shù)零點(diǎn)、方程的根以及函數(shù)圖象交點(diǎn)的等價(jià)關(guān)系上.

同時(shí)，我們注意到，在不能直接求解導(dǎo)數(shù)不等式的背景下，引入“令f′(x)=0”這一方法，先來討論導(dǎo)函數(shù)的零點(diǎn)(函數(shù)f(x)可能的極值點(diǎn))，再通過“逆向討論法”或“數(shù)形結(jié)合”的方式就可快速解決函數(shù)的單調(diào)性求解問題，這是最為有效的方法，也是通性通法.

3.類型三：含參數(shù)的函數(shù)單調(diào)性討論

當(dāng)導(dǎo)函數(shù)中含有參數(shù)，且該參數(shù)影響導(dǎo)函數(shù)的零點(diǎn)個(gè)數(shù)以及正負(fù)性時(shí)，需要帶著參數(shù)對導(dǎo)函數(shù)的影響進(jìn)行討論，這種類型的單調(diào)性討論往往伴隨著參數(shù)的影響而難以求解，下面介紹利用“導(dǎo)函數(shù)的零點(diǎn)討論法”求解此類問題.

3.1 含參函數(shù)的導(dǎo)函數(shù)為可因式分解型的求解策略

2021年高考中對此類問題的考查最為突出，下面來看例3.

【例3】(2021·新高考Ⅱ卷·22(Ⅰ))已知函數(shù)f(x)=(x-1)ex-ax2+b．

(Ⅰ)討論f(x)的單調(diào)性；

【解】(Ⅰ)由函數(shù)的解析式可得f′(x)=x(ex-2a)，令f′(x)=0，即x(ex-2a)=0.

故有x=0或ex=2a，

【注】下面分析方程ex=2a是否有解，以及有解后與另一解x=0的大小關(guān)系，這就是對參數(shù)a如何進(jìn)行討論的“切入點(diǎn)”.

①當(dāng)a≤0時(shí)，ex=2a無解，此時(shí)ex-2a>0，

故當(dāng)x∈(-∞,0)時(shí)，f′(x)<0,f(x)單調(diào)遞減，

當(dāng)x∈(0,+∞)時(shí)，f′(x)>0,f(x)單調(diào)遞增；

②當(dāng)a>0時(shí)，ex=2a的解為x=ln2a，故討論f′(x)=0的兩解：x=0與x=ln2a的大小關(guān)系，

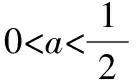
若x∈(-∞,ln2a)，則f′(x)>0,f(x)單調(diào)遞增；

若x∈(ln2a,0)，則f′(x)<0,f(x)單調(diào)遞減；

若x∈(0,+∞)，則f′(x)>0,f(x)單調(diào)遞增；

若x∈(-∞,0)，則f′(x)>0,f(x)單調(diào)遞增；

若x∈(0,ln2a)，則f′(x)<0,f(x)單調(diào)遞減；

若x∈(ln2a,+∞)，則f′(x)>0,f(x)單調(diào)遞增.

【評析】此題出現(xiàn)了導(dǎo)函數(shù)的零點(diǎn)討論，討論的“切入點(diǎn)”就是導(dǎo)函數(shù)方程“f′(x)=0”的解的個(gè)數(shù)及大小關(guān)系.通過對導(dǎo)函數(shù)的因式分解可以得到：導(dǎo)函數(shù)的零點(diǎn)一個(gè)是“定點(diǎn)”，一個(gè)是“動(dòng)點(diǎn)”(含參數(shù))，故可以通過分析“動(dòng)點(diǎn)”與“定點(diǎn)”的三種位置關(guān)系(即ln2a<0，ln2a=0，ln2a>0)來找到討論單調(diào)性的“切入點(diǎn)”，這樣的“討論依據(jù)”既可以做到對參數(shù)的討論“有理有據(jù)”“不重不漏”，又具有較強(qiáng)的邏輯性，再結(jié)合2.1,2.2的處理方法即可在含參數(shù)的背景下直接求出函數(shù)的單調(diào)區(qū)間，這是高考中對含參函數(shù)單調(diào)性考查的重難點(diǎn).

3.2 含參函數(shù)的導(dǎo)函數(shù)為不可因式分解型的求解策略

【例4】已知函數(shù)f(x)=ax3+3x2+3x(a≠0)．討論f(x)的單調(diào)性；

【解析】f′(x)=3ax2+6x+3，令f′(x)=0，即3ax2+6x+3=0，其判別式為Δ=36(1-a)，

①Δ=36(1-a)≤0時(shí)，即a≥1時(shí)，f′(x)≥0恒成立，故f(x)在(-∞,+∞)上單調(diào)遞增；

【注】此處Δ=0時(shí)，雖然f′(x)=0有一解，但該解不是函數(shù)f(x)的極值點(diǎn)，故可以與Δ<0合并討論.

②當(dāng)Δ=36(1-a)>0時(shí)，即a<1時(shí)，f′(x)=0有兩根，分別為x1,x2，不妨設(shè)

【注】此處先利用判別式Δ討論f′(x)=0的根的情況，在確定了二次方程f′(x)=0根的個(gè)數(shù)之后，進(jìn)一步確定二次函數(shù)的開口方向，從而清晰地得出原函數(shù)的單調(diào)區(qū)間，故此時(shí)應(yīng)將a<1分為a<0和0

故可得x1<0,x1

當(dāng)x∈(-∞,x1)∪(x2,+∞)時(shí)，f′(x)<0；

當(dāng)x∈(x1,x2)時(shí)，f′(x)>0,

所以f(x)在(-∞,x1)和(x2,+∞)上單調(diào)遞減，在(x1,x2)上單調(diào)遞增.

得x1<0，x2

當(dāng)x∈(-∞,x2)∪(x1,+∞)時(shí)，f′(x)>0；

當(dāng)x∈(x2,x1)時(shí)，f′(x)<0,

所以f(x)在(-∞,x2)和(x1,+∞)上單調(diào)遞增，在(x2,x1)上單調(diào)遞減.

綜上所述，當(dāng)a≥1時(shí)，f(x)在(-∞,+∞)上單調(diào)遞增；

【評析】例4與例3不同之處在于導(dǎo)函數(shù)對應(yīng)的零點(diǎn)不能直接求出，即導(dǎo)函數(shù)不可因式分解，從而難以求出零點(diǎn)，需借助二次方程的求根公式.同時(shí)在參數(shù)的影響下，還需考慮導(dǎo)函數(shù)零點(diǎn)的大小關(guān)系，綜合使用數(shù)形結(jié)合、分類討論的數(shù)學(xué)思想進(jìn)行綜合分析討論才能求解出函數(shù)的單調(diào)區(qū)間.從求解過程可以看出：導(dǎo)函數(shù)為含參數(shù)的二次型函數(shù)不可分解因式，可先根據(jù)判別式Δ的正負(fù)性來對二次方程的根的個(gè)數(shù)展開第一次討論；在確定了二次方程的根的個(gè)數(shù)的情況下，對二次函數(shù)的開口方向進(jìn)行第二次討論；在二次方程有兩根的情況下，需討論兩根大小關(guān)系進(jìn)行第三次討論，即可總結(jié)為“先Δ，后開口，最后比根大小”的討論模式.這樣的逐級先后對參數(shù)討論會(huì)使討論依據(jù)和切入點(diǎn)非常直觀，并且討論過程不重不漏，邏輯層次清晰，易于理解和掌握.

4.導(dǎo)數(shù)求解函數(shù)單調(diào)性策略的系統(tǒng)總結(jié)

導(dǎo)數(shù)作為求解可導(dǎo)函數(shù)單調(diào)區(qū)間的“神器”，其重心落在了求解導(dǎo)數(shù)大于(小于)0的不等式上.如果導(dǎo)數(shù)不等式可直接求解，則問題較為簡單;若導(dǎo)數(shù)不等式無法直接求解，則需借助“導(dǎo)函數(shù)的零點(diǎn)”(即先處理f′(x)=0是否有解問題，再處理f′(x)>0和f′(x)<0不等式問題)作為“切入點(diǎn)”，尤其含有參數(shù)討論函數(shù)單調(diào)性問題時(shí)，這種思維方法能夠引領(lǐng)學(xué)生迅速找到分類討論的突破口，從而不重不漏的在參數(shù)影響下解決函數(shù)的單調(diào)性問題.

結(jié)合對以上例子的分析以及求解策略的各自特點(diǎn)，我們可以總結(jié)得到利用導(dǎo)數(shù)求解函數(shù)單調(diào)性的系統(tǒng)方法：

(1)當(dāng)導(dǎo)函數(shù)中不含參數(shù)時(shí)，可歸納為以下求解步驟：

①求函數(shù)f(x)的導(dǎo)函數(shù)f′(x)；

②觀察f′(x)>0(<0)是否可以直接求解，若能，直接求出函數(shù)f(x)的單調(diào)區(qū)間；若不能轉(zhuǎn)入下一步；

③令f′(x)=0.

(ⅰ)若方程無解，則f′(x)在其定義域上恒大于(恒小于)0，即f(x)在其定義域上恒增或恒減；

(ⅱ)若方程有解，則在定義域范圍內(nèi)討論這些解(導(dǎo)函數(shù)的零點(diǎn))左、右區(qū)間上的導(dǎo)函數(shù)f′(x)的正負(fù)性(或采用數(shù)形結(jié)合觀察圖象討論f′(x)的正負(fù)性)，進(jìn)而求出函數(shù)f(x)的單調(diào)區(qū)間，這種方式也稱為“逆向討論法”，即利用導(dǎo)函數(shù)的零點(diǎn)將函數(shù)定義域分開，再討論不同區(qū)間上的導(dǎo)函數(shù)的正負(fù)性，進(jìn)而求出各區(qū)間上函數(shù)f(x)的單調(diào)性.

(2)當(dāng)導(dǎo)函數(shù)中含參數(shù)時(shí)，可歸納為以下步驟：

①求函數(shù)f(x)的導(dǎo)函數(shù)f′(x)，令f′(x)=0，考慮f′(x)=0的解是否受到參數(shù)影響，若參數(shù)取值不影響f′(x)=0的解，則直接求出單調(diào)區(qū)間;若影響，轉(zhuǎn)為第二步；

②求出f′(x)=0在其定義域內(nèi)的所有解.

(ⅰ)若f′(x)=0有一解，則在定義域范圍內(nèi)分析該解左、右兩側(cè)導(dǎo)函數(shù)的正負(fù)性即可求出單調(diào)區(qū)間；

(ⅱ)若f′(x)=0有兩解，則討論這兩解(含參數(shù))的大小關(guān)系，這是討論的“切入點(diǎn)”，一般有三種大小關(guān)系，在兩解位置關(guān)系確定的情況下，參數(shù)的取值范圍也就被確定了，進(jìn)而再利用“逆向討論法”求出單調(diào)區(qū)間；