2021年新高考數學多選題的解題策略與命題趨勢探析

安徽 張 超 王玉佩

多選題在高考數學中是一種創新題型，該題型為不同層次的考生提供了更多的得分空間，同時更加科學地發揮了高考的區分和選拔功能，為高校合理分層培養提供有效支撐，因而深受廣大師生的歡迎和關注.安徽省即將使用數學新高考卷,作為一線的一名數學教師，分析、研究多選題這一新題型的結構、特點，與總結探討多選題解題策略，非常有必要.為此，筆者結合2021年高考多選題的結構、特點及解題策略等三個方面談一下思考和認識，與讀者共同交流探討.

一、2021年新高考數學多選題的結構與特點

1.多選題的結構

多選題是高考數學三大題型之后在新高考數學卷中出現的一種新題型，全卷試題結構按單項選擇題、多項選擇題、填空題和解答題排列.所謂多選題就是圍繞一個主題，設計多個符合條件的正確選項供考生選擇，這是多選題和單選題的主要區別.新高考中多選題設置4 個選擇題，題號順序是第9題至第12題,每個選擇題設置4個選項，分別為A，B，C，D，每題滿分為5 分，共 20分.得分規則是“全部選對的得5分 ，有選錯的得0分，部分選對的得2分”.

2.多選題的特點

多選題具有分值小、解題思路廣的特點，和傳統單選題相比，多選題的設置給多數考生增加了得分機會，但是不容易得全分；考試中不免有考生因選出不正確選項而得0分；多數考生能夠選對部分正確選項得2分，因此多選題有較強的區分度，提升了考試的信度和效度.

下面結合2021年新高考Ⅰ卷試題加以剖析，旨在探索題型特點、規律，揭示解題策略.

二、多選題解題策略分析

1.直接法

從題設條件出發，運用有關概念、性質、定理、法則和公式等，通過正確的運算、推理或判斷，直接得出結論，從而得出正確答案的一種方法.運用此種方法解題需要扎實的數學基礎.

【例1】(2021·新高考Ⅰ卷·9)有一組樣本數據x1,x2,…，xn，由這組數據得到新樣本數據y1,y2,…，yn，其中yi=xi+c(i=1,2，…，n)，c為非零常數，則

( )

A.兩組樣本數據的樣本平均數相同

B.兩組樣本數據的樣本中位數相同

C.兩組樣本數據的樣本標準差相同

D.兩組樣本數據的樣本極差相同

B，若第一組數據的中位數為x，則第二組的中位數為x+c，顯然不相同，錯誤；

C，若第一組數據的方差為S2，則第二組數據的方差也是S2，故方差相同，正確；

D，由極差的定義知，若第一組的極差為xmax-xmin，則第二組的極差為ymax=(xmax+c)-(xmin+c)=xmax-xmin，故極差相同，正確，故選CD.

評注：該題是以統計知識為考查素材，只要統計概念清晰即可正確判斷.

通過該題說明老師在教學中要注重引導學生對平均值、方差概念的理解.因為在新高考中，越來越重視概念的考查.這也體現新高考注重基礎知識、基本技能及生活的考查理念.

2.綜合法

綜合法通常就是指應用直接法、特殊值法、排除法等,從而得出正確結論的方法.綜合法是解答數學多選題的常用方法.

【例2】(2021·新高考Ⅰ卷·10)已知O為坐標原點，點P1(cosα,sinα)，P2(cosβ,-sinβ)，P3(cos(α+β),sin(α+β))，A(1,0)，則

( )

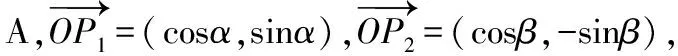
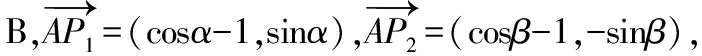
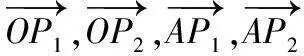
另外該題也可以采用數形結合法快速選出正確選項，通過該題需要注意解答多選題和單選題解法上有很大區別，比如解單選題時我們經常會采用所謂“投機取巧”的方法，例如,特殊值法、排除法、極端性原則等，這些方法解多選題就要慎用，多選題更加注重基本功和通性通法的考查.

3.數形結合法

數形結合是數學解題當中最常用的方法之一.運用數形結合思想，可以使抽象的數學問題變得更加生動、直觀，有助于學生把握數學問題的本質，這樣便使很多抽象的數學問題迎刃而解，讓“難懂”的解法變得容易理解和消化.

【例3】(2021·新高考Ⅰ卷·11)已知點P在圓(x-5)2+(y-5)2=16上，點A(4,0),B(0,2)，則

( )

A.點P到直線AB的距離小于10

B.點P到直線AB的距離大于2

詳解：圓(x-5)2+(y-5)2=16的圓心為M(5,5)，半徑為4，

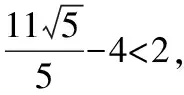
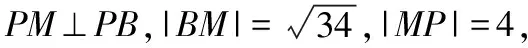
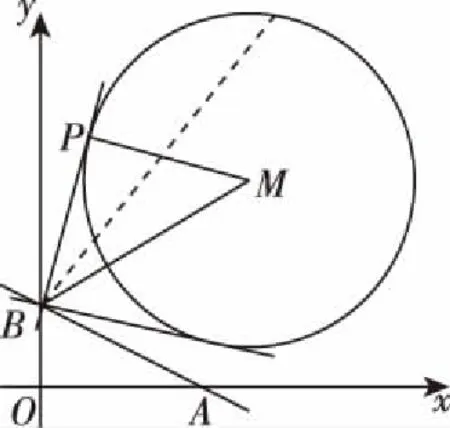
評注：本題是以直線與圓有關的最值相關知識點作為背景.由于圓既能與圓錐曲線相聯系,又能與平面幾何相結合,命題方式比較靈活,故與圓相關的最值問題備受命題者的青睞.在運動變化中,動點到直線、圓的距離會發生變化,在變化過程中,就會出現一些最值問題,如距離、角最小、最大等.這些問題常常聯系到平面幾何知識,利用數形結合思想可直接得到相關結論,解題時便可利用這些結論直接確定最值問題,故在此提醒考生解題時千萬不要得“意”忘“形”.

4.保底法

對于多選題中的壓軸題,難度一般較大,宜采用保底法，即當有些選項在一定時間無法確定是否正確時，可選定其他正確的一個保住基本分，因為部分選對也可得2分(這比單選題的得分概率要高)，我們把這種解題策略稱為保底法.當然,如果學生整體素質較高,或者對題目十分熟悉,則另當別論．

( )

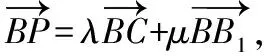
A.當λ=1時，△AB1P的周長為定值

B.當μ=1時，三棱錐P-A1BC的體積為定值

詳解：易知，點P在矩形BCC1B1內部(含邊界)．

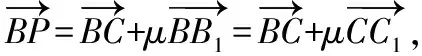
評注：本題是以立體幾何知識為素材，屬于選擇題中的壓軸題.多選題中的立體幾何試題，常把多個知識點交匯考查，如把幾何體長度、角度、面積、體積的計算與線面位置關系結合在一起考查，也可與函數、不等式及空間向量結合在一起考查，此類問題對學生直觀想象及邏輯推理的核心素養要求較高，難度也比較大.

三、多選題命題趨勢和教學啟示

通過2021年新高考Ⅰ卷試題分析，筆者得到如下教學啟示：

1.從命題角度看，該試題是以統計、三角函數、向量、圓錐曲線(直線和圓)、立體幾何綜合問題等為背景進行試題設計，其主要原因是三角函數圖象和性質等特點多樣，命題入手點相對較寬,直線和圓試題中數形結合動態分析能夠較好地體現區分度.但是從命題的著手點來看新高考相對于舊高考有了較大的變化，命題的載體向生活化、靈活化傾斜等，所以還是不能偏頗的認為只有這些載體，例如考查以初等基本函數為載體，加絕對值等手段考查函數性質等等，但是不論新高考如何變化老師在教學中還是要強調基礎的穩固，適當的延伸，關注情境和生活化的試題，注重重大考試的變式演練.

2.從解題策略角度看，2021年新高考多選題分別用到了常用的直接法、綜合法、數形結合法、保底法等.在解題策略上更加注重通性通法，對學生基礎知識和解題技巧要求更高.

3.從數學核心素養角度看，2021年新高考試題對于數學核心素養的考查比較全面，其中數學運算、邏輯推理核心素養的考查力度很大，所以在以后新高考中對數學核心素養的考查會更加全面，這就要求一線老師在教學中注重數學核心素養的滲透.

四、結語