基于區間值中智軟集合的突發事件下彈性供應商選擇方法研究★

張國業，侯晨靜，董媛香

（1.山西省數字政府服務中心，山西 太原 030031；2.太原工業學院經濟與管理系，山西 太原 030013；3.太原理工大學經濟管理學院，山西 太原 030024）

引言

新型冠狀病毒肺炎（COVID-19）疫情的突然爆發和蔓延，迫使人員隔離和交通運輸阻隔，全球大量企業停工停產對供應鏈造成了極大威脅。在全球經濟一體化的背景下，供應鏈呈現相互依存且利益關系錯綜復雜的網狀結構，企業為應對激烈的國際競爭，常常采用準時生產方式（JIT）及供應商管理庫存（VMI）等供應鏈管理模式，當面對疫情等破壞性大且損失規模難以控制的突發事件時，任何一個供應商的阻斷都會對整個供應鏈網絡造成不可逆轉的威脅。

因此在突發事件背景下，選擇一個更有彈性的供應商，可以在供應鏈受到擾動或中斷后迅速恢復其原始或達到更佳狀態[1]。彈性供應商本質是具備比競爭對手更好地應對風險和意外事件的能力[2]。然而，突發事件的低概率和高強度特征決定了突發事件下彈性供應商選擇具有高度不確定性，也使得該決策問題更加復雜[3]。一些學者采用隨機模型來研究不確定環境下的彈性供應商選擇問題，使用最廣泛的方法是兩階段隨機規劃模型[4]和雙目標規劃模型[1，5]。然而，隨機模型在處理大量屬性數據和群體決策過程中模糊性方面沒有優勢。因此，另外一些學者利用模糊集及其擴展方法探討不確定環境下的彈性供應商選擇問題。其中，模糊集和TOPSIS 結合的方法引起廣泛關注[3-6]。

雖然基于模糊集的決策方法在彈性供應商選擇中具有良好的應用效果，但模糊集與概率論、粗糙集和區間數學理論均存在參數化不足的缺陷，因此Molodtsov[7]提出了軟集合理論解決這一問題。此外，軟集合還具有對數據類型沒有限制且可以直接建立近似模型快速求解的優勢。目前，軟集合已被成功應用到數據挖掘[8]、組合預測[9]和決策問題[10]等方面；相關理論也得快速發展，逐步擴展到模糊軟集合[11]、次協調軟集合[12]和中智軟集合[13]等各種類型的軟集合。其中，中智軟集合可以表示數據的隸屬度、不確定度和非隸屬度，進一步擴大了不確定數據的描述范圍，可以解決包含沖突信息的復雜不確定問題。考慮到在不確定環境下，用區間值代替精確值來處理隸屬度更實用，Deli[14]進一步提出了區間中智軟集合的概念。

綜上，本文考慮到突發事件背景下的高度不確定性，以及決策信息存在沖突等復雜情況，采用可以表示不確定性和沖突性的區間值中智軟集合作為彈性供應商選擇的基本方法，并提出區間值中智軟集合的確定程度、沖突程度以及鄰近度測度概念及方法。基于鄰近度、熵權法和組合賦權的思想分別測度專家權重，參數客觀權重和參數綜合權重。最后，考慮到專家決策的心理因素，結合前景理論（Prospect Theory）構建了基于區間值中智軟集合的突發事件下彈性供應商選擇群決策模型，并通過實例驗證該方法的可行性。

1 預備知識

定義1[15]令U 為初始論域，u 為論域U 中的任意元素，定義在論域U 上的區間值中智集A={＜u，TA（u），IA（u），FA（u）＞，u∈U}（T，I，F：U→[0，1]）包含元素u 對于區間值中智集A 的隸屬度TA（u），不確定程度IA（u）和非隸屬度FA（u）。其中，TA（u）=[infTA（u），supTA（u）]，IA（u）=[infIA（u），supIA（u）]，FA（u）=[infFA（u），supFA（u）]。且對于?u∈U，均滿足0≤supTA（u）+supIA（u）+supFA（u）≤3。

為方便起見，我們用A（u）=＜[infTA（u），supTA（u）]，[infIA（u），supIA（u）]，[infFA（u），supFA（u）]＞表示元素u對于區間中智集A 的隸屬程度，并稱A（u）為一個區間值中智數。

定義2[14]令U 為初始論域，E 為參數集。設P（U）為論域U 上所有區間值中智集的集合，稱（F，E）為論域U 上的一個區間值中智軟集合，當且僅當F 是E 到P（U）所有子集的一個映射，記作F∶E→P（U）。

定義3[16]區間值中智數A（u1）和A（u2）間的標準化漢明距離為：

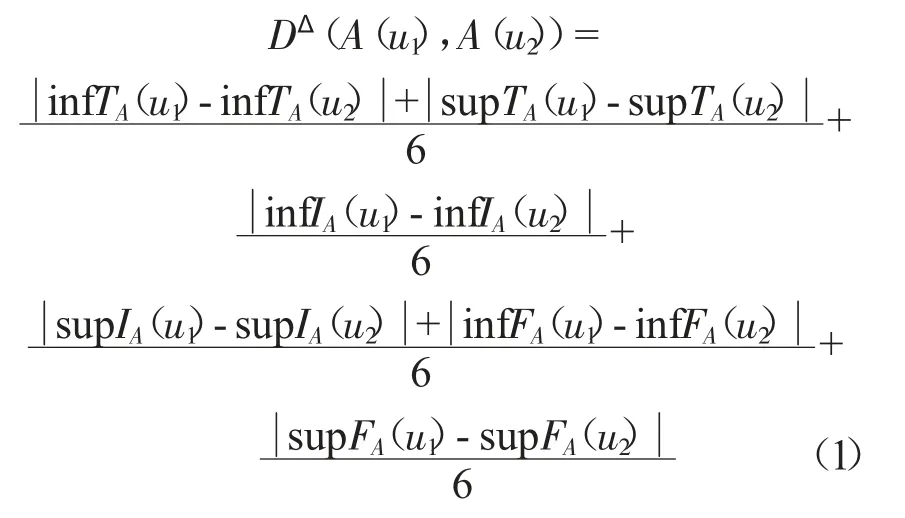
2 區間值中智軟集合相關運算

2.1 確定程度和沖突程度測度

定義4 令min=＜[1，1]，[0，0]，[0，0]＞為最小沖突區間值中智數，表示對象對于集合的隸屬度為1，不確定程度和非隸屬度均為0，即信息沖突程度最小。

定義5 令max=＜[0.5，0.5]，[1，1]，[0.5，0.5]＞為最大沖突區間值中智數，此時隸屬度和非隸屬度均為0.5，不確定度為1，即信息沖突程度最大。

定義6 設A（u）=＜TA（u），IA（u），FA（u）＞為一個區間值中智數，其中TA（u）=[infTA（u），supTA（u）]，IA（u）=[infIA（u），supIA（u）]，FA（u）=[infFA（u），supFA（u）]，則A（u）的確定程度定義為：

可知，確定程度衡量的是區間值中智數A（u）與最小沖突區間值中智數min 之間的標準化漢明距離。中智數A（u）與min 之間的距離越小，確定程度越大；反之，確定程度越小。類似地，將區間值中智數A（u）與max 之間的標準化漢明距離衡量A（u）的沖突程度。

定義7 設A（u）=＜TA（u），IA（u），FA（u）＞為一個區間值中智數，其中TA（u）=[infTA（u），supTA（u）]，IA（u）=[infIA（u），supIA（u）]，FA（u）=[infFA（u），supFA（u）]，則A（u）的沖突程度定義為：

可知，區間值中智數A（u）與max 之間的距離越小，沖突程度越大；反之，沖突程度越小。

2.2 鄰近度測度

定義8 假定集合U={u1，u2，...，ui，...，um}為論域，E={e1，e2，...，ej，...，en}為參數集，（F，E）和（G，E）為論域U 上的兩個區間值中智軟集合。

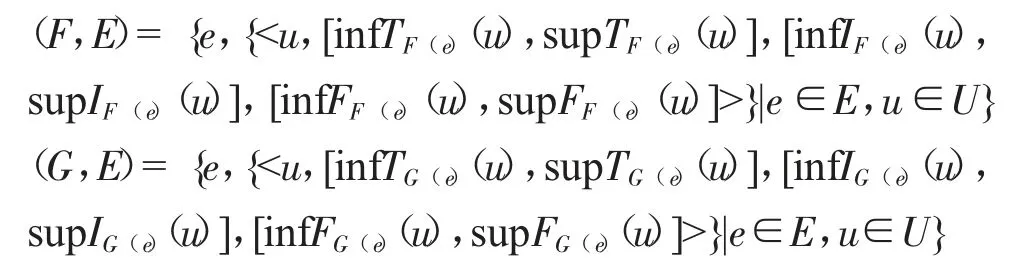
則（F，E）和（G，E）之間的鄰近度測度為：

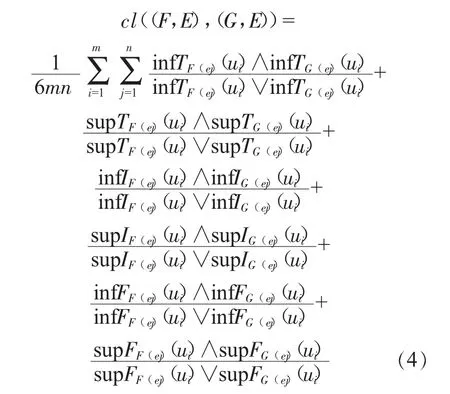
其中，∧表示兩者之間取最小值；∨表示兩者之間取最大值；且cl（（F，E），（G，E））∈[0，1]，當cl（（F，E），（G，E））越接近于0 時，表明區間值中智軟集合（F，E）和（G，E））之間的鄰近度越低；反之，鄰近度越高。

3 突發事件下彈性供應商選擇的群決策方法

3.1 問題描述

設U={u1，u2，...，ui，...，um}為候選供應商集，E={e1，e2，...，ej，...，en}為供應商彈性參數集，R={r1，r2，...，rl，...，rz}表示專家集，z 個專家分別給出評估彈性供應商的區間值中智軟集合為（Fl，E）（l=1，2，...，z），用區間中智數=＜FFl（ej）（ui），IFl（ej）（ui），FFl（ej）（ui）＞（i=1，2，...，m；j=1，2，...，n；l=1，2，...，z) 表示專家rl對備選彈性供應商ui關于某個彈性指標參數ej的評價值。其中，TFl（ej）（ui）=[infTFl（ej）（ui），supTFl（ej）（ui）]，IFl（ej）（ui）=[infIFl（ej）（ui），supIFl（ej）（ui）]，FFl（ej）（ui）=[infFFl（ej）（ui），supFFl（ej）（ui）]。

3.2 決策過程

3.2.1 專家權重的確定

本文基于鄰近度思想構建專家權重模型。

首先，構建z 個專家rl對候選供應商彈性指標評價值的區間值中智軟集合（Fl，E）（l=1，2，...，z）。

其次，計算各個專家給出的供應商彈性指標評價值均值的區間值中智軟集合，則有：

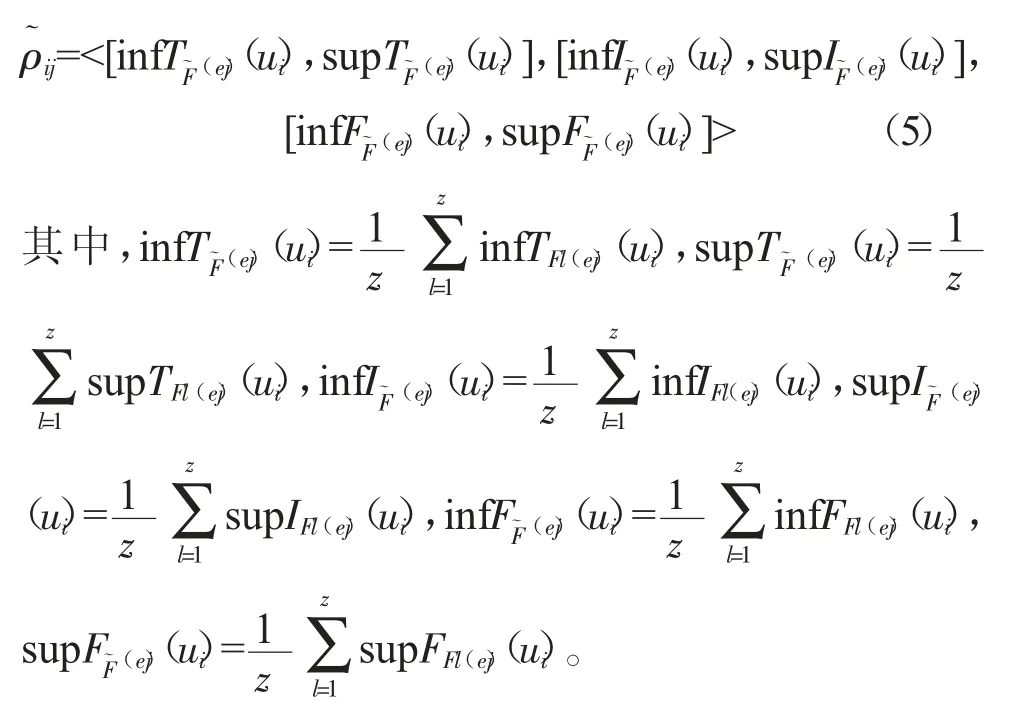
在此基礎上，依據公式（4），測度區間值中智軟集合（Fl，E）（l=1，2，...，z）與之間的鄰近度，鄰近度越高，專家權重越大。

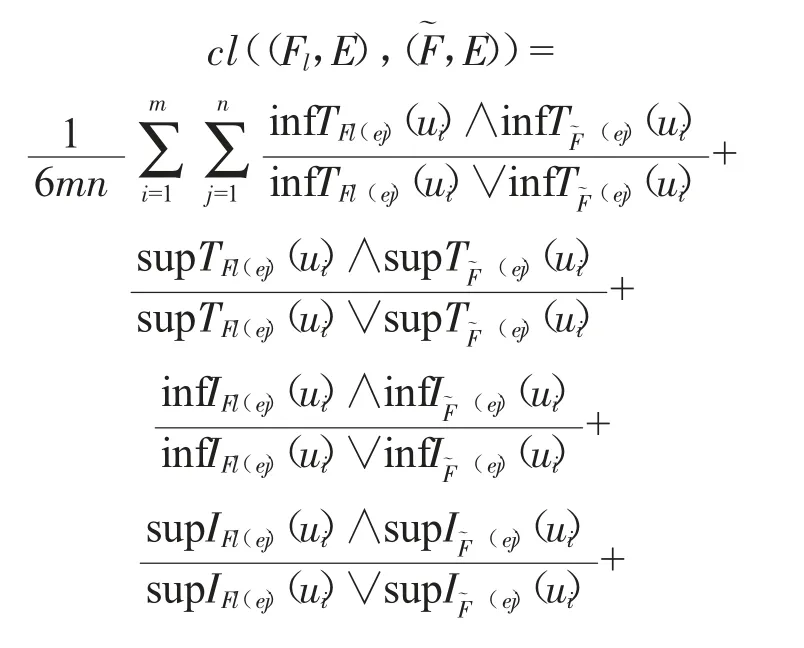
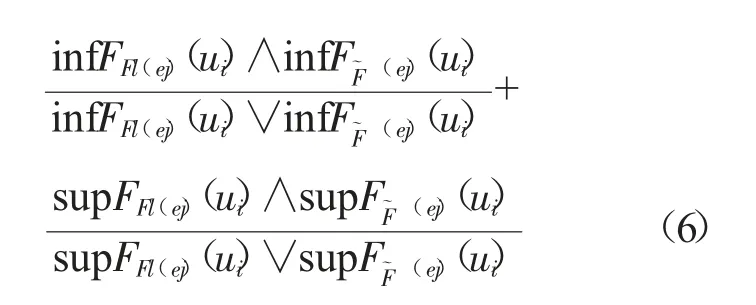
最后，計算專家權向量φ={φ1，φ2，...，φl，...，φz}。其中，

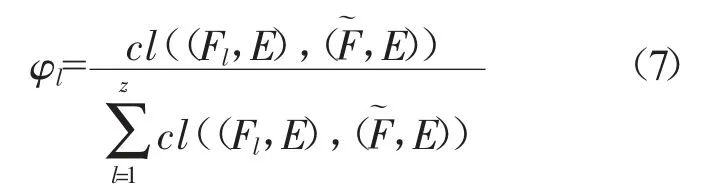
3.2.2 參數綜合權重的確定

3.2.2.1 參數客觀權重計算

當屬性值不相等且權重未知時，利用熵測度可以確定屬性的客觀權重，信息熵越小則各供應商之間該彈性指標差異越大，權重越大。本文采用基于信息熵的客觀賦權法——熵權法[17]，可推斷專家rl（l=1，2，...，z）給出的區間中智軟集合（Fl，E）中參數ej（j=1，2，...，n）的熵值為：

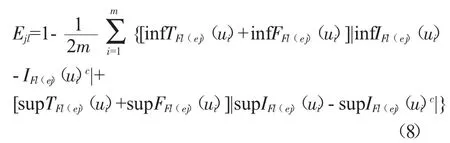
則參數ej的熵值為：

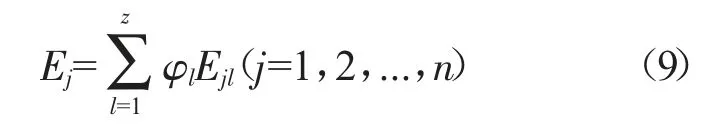
其中，φl表示專家的權重。

故參數ej的客觀權重值為：

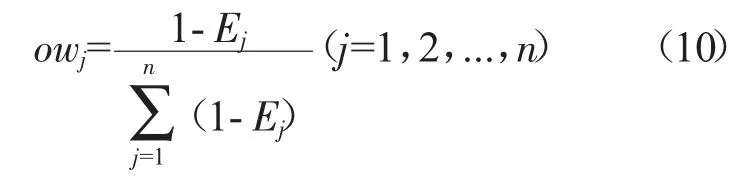
3.2.2.2 參數綜合權重值計算

本文采用組合賦權的方式，基于最小信息熵原理將主觀權重和客觀權重結合得到參數綜合權重。這里假定參數的主觀權重直接由專家給定，令參數主觀權向量為SW={sw1，sw2，...，swj，...，swn}，客觀權向量為OW={ow1，ow2，...，owj，...，own}，則參數的綜合權向量為ω={ω1，ω2，...，ωj，...，ωn}，其中：

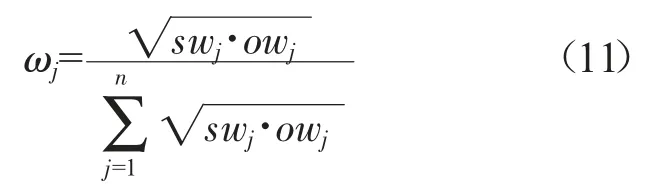
3.2.3 前景理論綜合前景值的計算

在具有風險和不確定條件下進行選擇時，專家的行為并非完全理性，評價結果與其心理風險感知有關，本文引入前景理論[18]將專家的主觀心理偏好納入彈性供應商選擇中。基于前景理論，各彈性供應商的綜合前景值Vi由前景決策矩陣中各彈性供應商對于各參數的前景值Vij和參數綜合權重ωj共同決定。

3.2.3.1 前景決策矩陣構建

前景決策矩陣構建的核心是計算價值函數v（x-r）和決策權重函數ω（p）。價值函數v（x-r）計算方式如下：

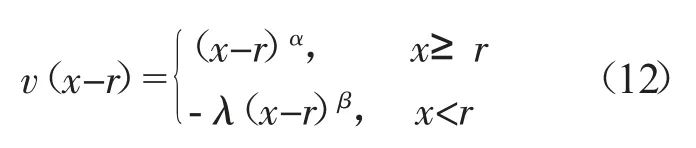
決策權重函數ω（p）計算方法如下：

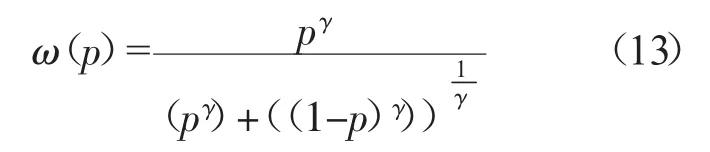
其中，p 為判斷概率，考慮突發事件下彈性供應商問題由專家評價，故將本文計算的專家權重φl視為判斷概率p；γ 為風險態度系數，根據Tversky和Kahneman[36]實驗驗證得參數γ 的最優取值為：γ=0.61。

則前景決策矩陣中各彈性供應商ui相對于各參數ej的前景值為：

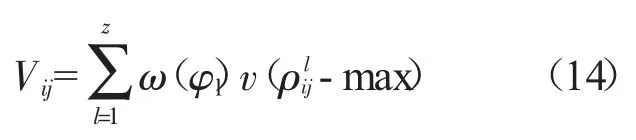
其中，i=1，2，...，m；j=1，2，...，n。

3.2.3.2 綜合前景值計算

基于參數綜合權重和前景決策矩陣，各供應商ui的綜合前景值可通過下式計算：

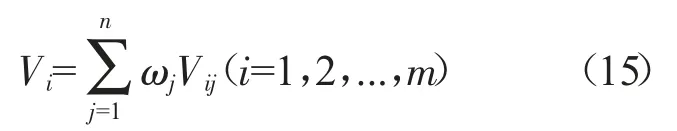
4 實例分析

4.1 實例背景

M公司一家主要設計生產加工高新技術醫療設備和新型精密醫療儀器的公司，并銷往全球各地。隨著制造全球化和知識經濟的發展，為應對市場環境變化，M公司選擇自己專注于生產核心部件，而從全球角度配置非核心流程的優質原材料及零部件，降低成本的同時對供應商依賴性增強。然而，M公司的供應鏈網絡數量龐大且跨越全球，國際供應商易受到突發事件的影響，導致供應鏈中斷。近年來頻發的突發事件也使得M 公司在選擇供應商時更加聚焦于適應不同需求的“彈性”指標，以改善供應鏈風險管理，有效地預防和應對突發事件造成的中斷。M公司對供應商的要求有：能夠承受供應鏈網絡的中斷，通常有一個現成的或者可以快速實現的替代商；能夠對市場變化做出快速反應，通常有一個能快速處理意外或不穩定需求的合作伙伴；只包含少量或不包含浪費，以較少的投入提供高價值的產品；能夠靈活地適應外界的干擾而沒有較高的成本或較長的交貨時間。因此，M公司選擇具有穩健性（robust）、敏捷性（agile）、精益性（lean）和柔性（flexible）這四個指標組成“RALF 標準”作為彈性供應商評價指標。M 公司根據要求對候選供應商進行評估，最終有三家供應商可供選擇，并邀請三位專家根據“RALF”這四個指標來選擇最優供應商。假定U={u1，u2，u3}為三家備選供應商組成的集合，E={e1，e2，e3，e4}為描述供應商彈性的參數集合，其中四個參數分別表示“RALF”四個指標，三位專家集合用R={r1，r2，r3}表示。現在M公司基于三位專家給出的供應商彈性指標的數據對三家供應商進行評價并做出合作決策。其中，專家給出的參數的主觀權重向量為sw={0.1，0.5，0.3，0.1}。

4.2 群決策過程

步驟1：構建表示專家對三家供應商彈性評價信息的區間值中智軟集合（F1，E），（F2，E）和（F3，E）。

步驟2：本實例參數均為效益型成本，故無需對（Fl，E）（l=1，2，3）進行標準化處理。

步驟3：依據公式（7）計算專家權向量。

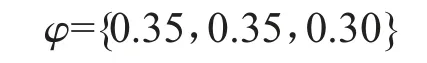
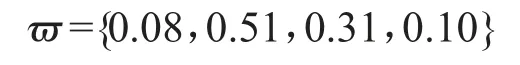
步驟5：依據公式（14）構建前景決策矩陣。

步驟6：依據公式（15）計算各彈性供應商的綜合前景值Vi。

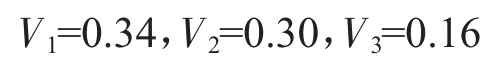
步驟7：依據各供應商的綜合前景值對其進行排序并做出選擇決策。

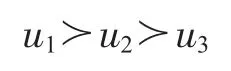
因此，u1為最優彈性供應商，u2次之，u3最劣。

5 研究結論

本文提出方法的優越性和創新性主要表現為以下四點：

1）選擇可以充分描述多維不確定和沖突信息的區間值中智軟集合作為彈性供應商選擇的基本方法，以應對突發事件下的復雜不確定環境。同時，相應地提出了區間中智軟集合的確定程度、沖突程度以及鄰近度測度概念及方法。

2）考慮到參數重要程度的差異，采用組合賦權方式對參數賦權。具體地，主觀權重由專家直接給定，客觀權重用熵權法計算得出，進而基于最小信息熵原則將主觀和客觀權重相結合得到參數綜合權重。

3）采用群決策方式對供應商進行評估，以更加全面客觀地分析供應商的彈性指標狀況，其中專家權重根據區間值中智軟集合的鄰近度進行測度。

4）充分考慮了突發事件下決策者的非理性因素對供應商彈性評價結果的影響，基于前景理論構建了彈性供應商選擇模型。