基于SPH方法的組合射流破巖模擬研究*
廖翔云 馬小晶 周新超 齊思維 李宏煜
(新疆大學電氣工程學院)
0 引 言
頁巖氣儲層普遍具有低滲透的特性,為了大規模開采,必須改善其儲層滲透性[1-2]。水力壓裂技術有利于提高油氣層滲透率,在低滲透油藏的高效開采領域有著較好的應用前景[3-5]。
在計算機理論與技術發展的背景下,數值模擬方法已成為研究水力壓裂技術的有效手段之一。雷光宇等[6]運用有限元方法,研究了不同井深條件下射流速度對破巖效率的影響;蔣斌等[7]采用ALE方法對水射流破土進行數值模擬,分析了淹沒條件及非淹沒條件下沖坑演化的差異。然而,基于網格的數值模擬方法在處理大變形和高應變率的射流破巖問題時,網格會發生扭曲和畸變,使求解精度降低,甚至導致計算終止。因此,研究并采用一種合理有效的數值模擬方法,對實現射流破巖的準確模擬,以及找到影響破巖效果的主要因素十分必要。
目前,無網格方法逐漸受到國內外研究學者的廣泛關注[8-9]。光滑粒子流體動力學(SPH)方法作為典型的無網格法之一,運用可運動的粒子離散所求解的計算域,適合模擬變形邊界和大變形的問題[10]。司鵠等[11]采用SPH方法分析了脈沖射流破巖過程中應力波的形成、傳播及衰減特性。趙健等[12]采用SPH方法研究并得到了粒子射流參數對破巖體積的影響規律。
組合射流作為常用的水射流鉆進技術,在超短半徑轉向鉆孔方面優勢顯著。目前,已有學者對組合射流破巖過程展開了研究[13],揭示了組合射流沖擊破巖機理,但對于組合射流破巖能力與射流參數關系的探究還相對較少。鑒于此,本文基于SPH方法構建了組合射流破巖模型,模擬研究了射流參數(射流噴距、射流直徑和射流軸向傾角)對組合射流破巖能力的影響。研究結果可為實際工程應用提供一定的理論依據。
1 SPH方法基本理論
SPH方法是一種以插值理論為基礎的純拉格朗日方法。對于本文所研究的問題,將水射流和巖石離散成一系列攜帶各種物理量的可自由運動的粒子,以求解各種邊界條件下的偏微分方程,因此任一宏觀變量可由一組離散點的值得到積分插值。利用近似法將偏微分方程轉換成積分形式的方程[14-15]:
(1)
式中:Ω為整個求解區域;W(x-x′,h)為光滑核函數;h為粒子的光滑長度,決定支持域的大小;x-x′為空間點與所求場函數值點之間的距離。
利用粒子近似法將連續積分方程(1)轉換成離散形式的方程:
(2)
式中:mj為粒子j的質量,ρj為粒子j的密度。
本文采用較為常用的三次B樣條核函數[16]:
(3)
式中:C是由空間維度確定的標準化常量,由歸一化條件確定,C取1/(πh3)。
2 射流破巖模型的建立及參數設置
針對研究的組合射流沖蝕巖石的問題,做出如下基本假設:忽略氣相因素對水射流的影響,水射流無散射現象;巖石為連續介質,孔隙和裂紋等不影響組合射流破巖;整個射流破巖過程中只涉及水和巖石兩種物質。
2.1 組合射流模型
水射流采用MAT_NULL本構模型,將其視為完全塑性材料,賦予其Gruneisen狀態方程[17],即有:
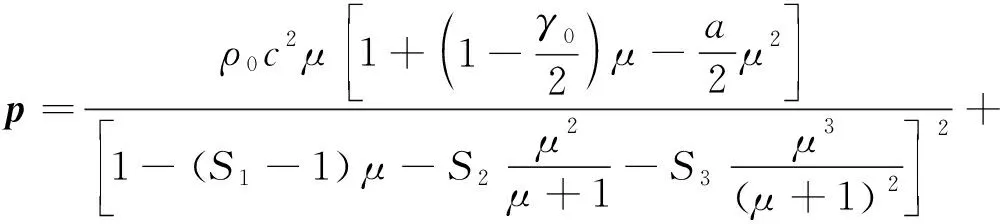
(4)
式中:p為沖擊壓力,a為一階體積修正量,γ0為Gruneisen常數,c為沖擊波速度-質點速度曲線的截距,E為單位體積內能,μ為流體黏性系數,S1、S2和S3為沖擊波與質點速度變化曲線的斜率。
水的本構參數為:ρ0=1 050 kg/m3,c=1 647 m/s,S1=1.921,S2=-0.096,S3=0,γ0=0.35,a=0,E=0。
2.2 巖石模型
為了滿足大變形、高應變率和高拉壓效應的巖石工況假設需要,本文引入該模型對巖石進行描述。H-J-C本構模型綜合考慮了巖石材料損傷、應變率和靜水壓力對屈服力的影響,其強度以規范化等效應力描述為[18]:
(5)
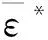
損傷度計算如下:
(6)
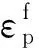
其中,頁巖參數為:ρ=2 440 kg/m3,A=0.79,B=1.6,C1=0.007,N=0.6。
2.3 幾何模型及邊界條件
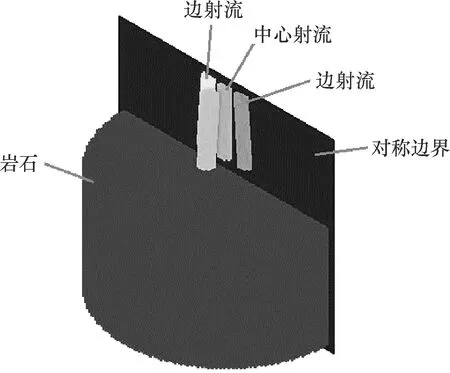
圖1 組合射流沖蝕巖石模型Fig.1 Model of rock breaking by combined jets
3 破損坑指標的定義
為了合理描述組合射流沖蝕巖石的破損效果,本文對破損坑進行了特征提取,定義破損坑指標并進行無量綱化處理,分別為:坑縱截面面積(a/A)、表面坑徑(w/W)和最大坑深(h/H)。破損坑指標參數示意圖如圖2所示,其中a、w和h分別為破損坑縱截面面積、表面坑徑和最大坑深,A、W和H分別為巖石初始的縱截面面積、寬度和高度。
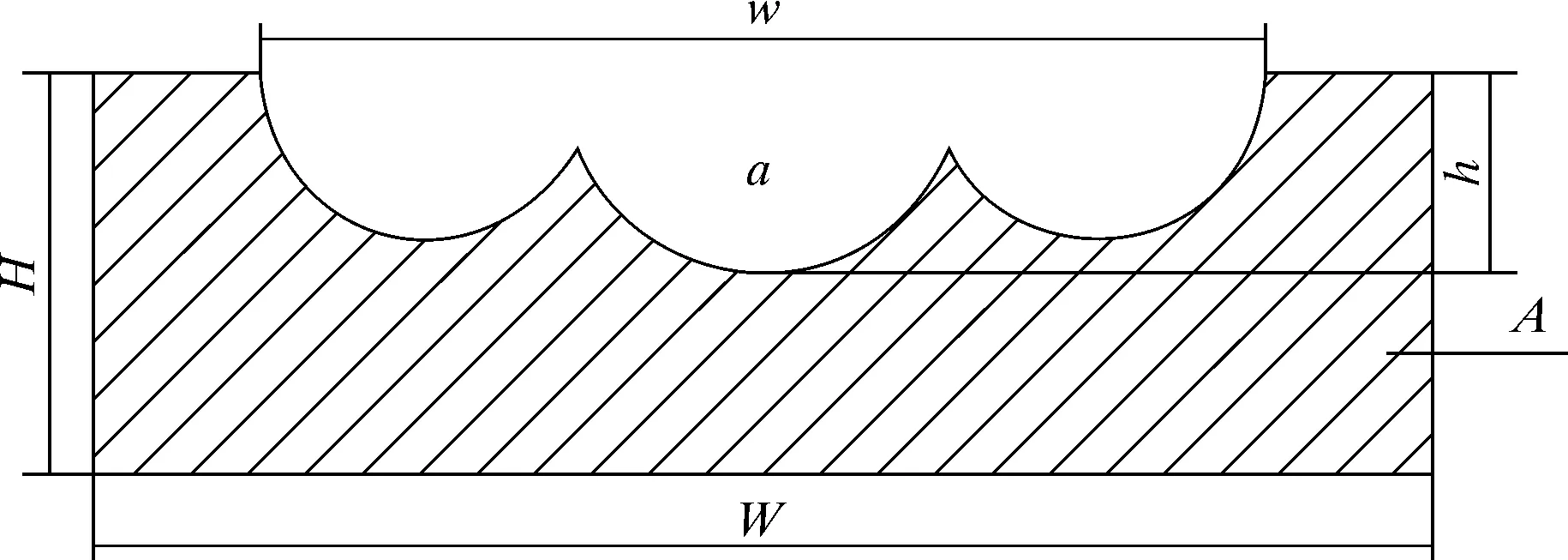
圖2 破巖指標參數示意圖Fig.2 Diagram of rock breaking index parameters
4 計算結果分析
4.1 驗證模型有效性
為了驗證所建模型的有效性,本文對周哲[13]研究的組合射流沖擊破巖的動態過程進行了模擬,所取參數與該研究保持一致,射流直徑D1為0.8 mm,軸向偏角β為12°,射流間距d為2 mm,初速度v為245 m/s。圖3是組合射流沖擊破巖過程中破損坑及應力波的演化情況。
由圖3可知,在時間t為0.01 ms時,射流沖擊巖石表面產生極大的瞬時接觸應力并出現破損坑,此時中心射流與邊射流沖擊形成的破碎坑間有凸臺。應力波以接觸處為中心呈球形波向四周傳播,隨著沖蝕時間的延續,應力波擴散至整個巖體,同時中心射流與邊射流之間的凸臺導通,形成聯合破碎坑。
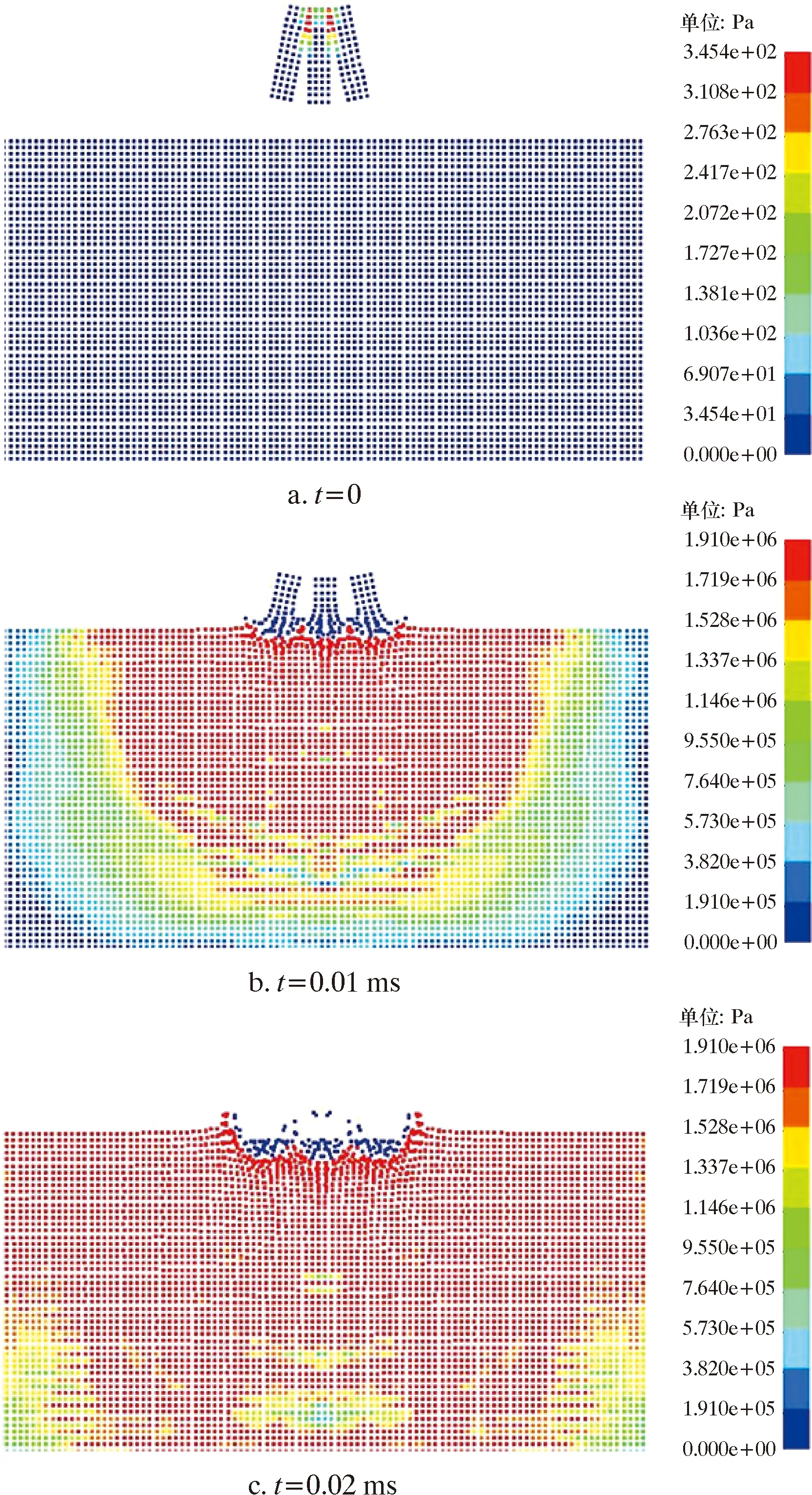
圖4表示0.05 ms時巖石縱截面的破損坑情況以及周哲[13]研究所得的巖石CT掃描試驗結果。
由圖4可知,該模型的模擬結果與CT掃描試驗結果的破損坑形狀非常接近,從而驗證了本研究所構建的組合射流沖蝕巖石數值模型的有效性與合理性。

圖4 仿真結果與試驗結果對比圖Fig.4 Comparison between simulation results and experimental results
4.2 射流噴距的影響
射流噴距是影響組合射流破巖能力的重要因素之一,模擬研究中射流噴距l取1~5 mm,射流直徑D1為1.2 mm,射流軸向傾角β為4°,射流間距d為2 mm。
圖5表示射流速度v為550 m/s時不同射流噴距下巖石的破損圖。從圖5可以看出,當射流噴距l≤4 mm時,隨著射流噴距的增大,破損坑縱截面面積不斷增大,即破巖能力增強;但是當射流噴距l≥5 mm時,巖石破損坑底部的凸臺較為明顯。為了進一步分析射流噴距對破巖效果的影響,圖6給出了不同射流速度下射流噴距與巖石破損坑縱截面面積、最大坑深及表面坑徑的變化曲線。
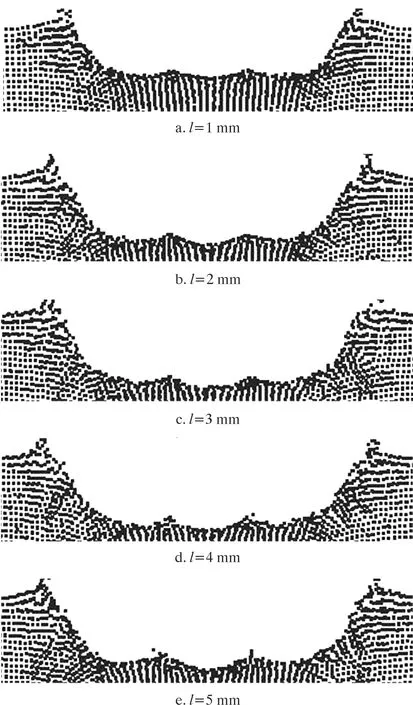
圖5 不同射流噴距下巖石的破損圖(t=0.05 ms)Fig.5 Rock damage under different jet distances(t=0.05 ms)
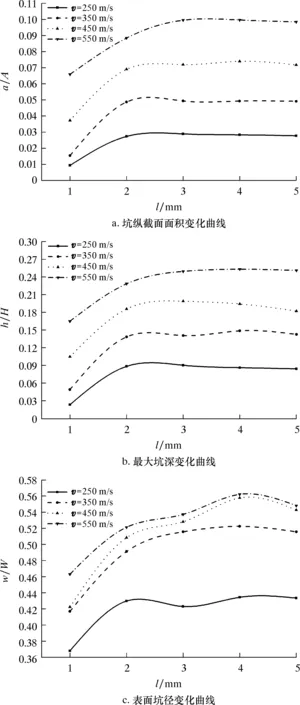
圖6 不同射流噴距下巖石破損坑指標變化曲線(t=0.05 ms)Fig.6 Variation of rock damage pit index under different jet distances (t=0.05 ms)
從圖6可以看出,隨著射流噴距的增大,巖石破損坑縱截面面積和最大坑深呈先急劇增大后減小的趨勢。這是因為當射流噴距較小時,射流沖擊巖石產生的回流會造成干擾,消耗射流的沖擊能量,使得破損坑縱截面面積較小;隨著射流噴距的增大,回流對射流的干擾作用逐漸減弱,從而破損坑縱截面面積不斷增大;但當射流噴距過大時,射流與巖石表面接觸時的間距過大,應力波干涉作用減弱,使得破巖效果減弱。由此可知:射流噴距存在一個使得巖石破損效果最大的最優值范圍,該最優數值范圍為3~5 mm。當射流噴距增加時,巖石表面坑徑先增大后減小,特別是在射流速度大于250 m/s后,巖石表面坑徑急劇增大,這也說明增大射流速度能夠提高巖石的破碎效率。
4.3 射流直徑的影響
射流直徑也會影響組合射流的破巖能力,模擬中射流直徑D1取0.8~2.0 mm,射流噴距l為1 mm,射流軸向傾角β為4°,射流間距d為2 mm(研究中保持射流粒子數大致相同,相差小于2%,因此忽略射流粒子數對研究結果的影響)。圖7表示射流速度v為550 m/s時不同射流直徑下巖石的破損圖。
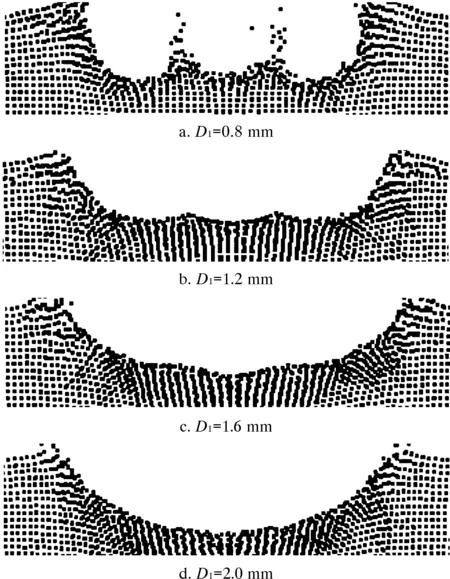
圖7 不同射流直徑下巖石的破損圖(t=0.05 ms)Fig.7 Rock damage under different jet diameters (t=0.05 ms)
從圖7可以看出,射流直徑的大小會顯著影響巖石破損坑形狀,直徑較小時,巖石破損坑底部的凸臺較為明顯,隨著射流直徑的增大,凸臺逐漸消失,破損坑形狀逐漸趨于弧形。為了進一步分析射流直徑對破巖效果的影響,圖8給出了不同射流速度下射流直徑與巖石破損坑縱截面面積、最大坑深及表面坑徑的變化曲線。
從圖8a可得,巖石破損坑縱截面面積隨著射流直徑的增大而不斷增大,且增大射流速度會使得破損面積的增幅變大。由圖8b可知,在不同射流速度下,射流直徑的大小對破巖最大坑深的變化影響較小,尤其是在射流速度較低時,其變化甚微,因此射流速度是影響破巖最大坑深的主要因素。由圖8c可知,當射流直徑增加時,巖石表面坑徑先增大后減小。這說明射流直徑過大時,由于相鄰射流間距較小,射流沖擊過程中相互干擾消耗能量,造成破巖坑徑減小。因此應當合理選擇射流直徑,以達到最佳破巖效果。
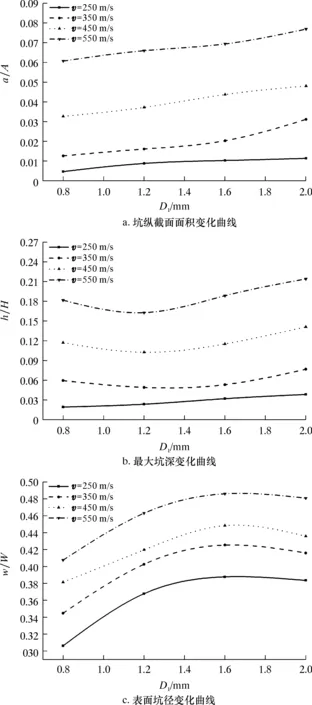
圖8 不同射流直徑下巖石破損坑指標變化曲線(t=0.05 ms)Fig.8 Variation of rock damage pit index under different jet diameters (t=0.05 ms)
4.4 射流軸向傾角的影響
本文模擬研究了射流軸向傾角對破巖效果的影響,研究中射流軸向傾角β取2°~10°,射流噴距l為1 mm,射流直徑D1為1.2 mm,射流間距d為2 mm。圖9表示射流速度v為550 m/s時不同射流軸向傾角下巖石的破損圖。
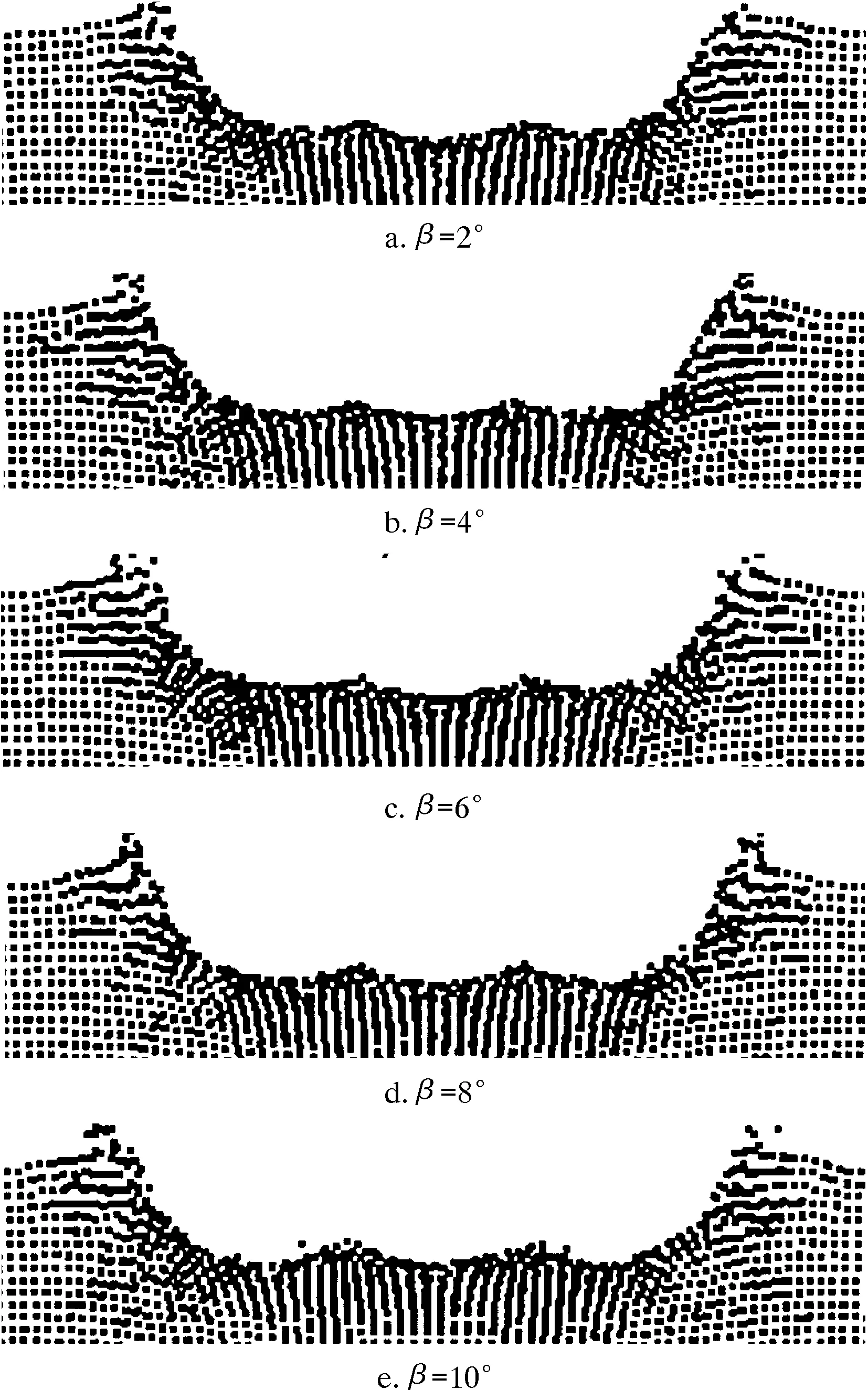
圖9 不同射流軸向傾角下巖石的破損圖(t=0.05 ms)Fig.9 Rock damage under different jet axial inclinations (t=0.05 ms)
由圖9可知,當射流軸向傾角增加時,射流作用范圍增大,造成巖石表面坑徑不斷增大,射流沖擊區域形成了聯合破碎坑。為了進一步分析射流軸向傾角對破巖效果的影響,圖10給出了不同射流速度下射流軸向傾角與巖石破損坑縱截面面積、最大坑深及表面坑徑的變化曲線。
從圖10a可以看出,射流軸向傾角的變化對破損坑縱截面面積的影響很小,可近似忽略。
由圖10b可知,在低速沖擊破巖時,射流軸向傾角幾乎不會影響破巖深度,但當射流速度增大到一定值時,巖石最大坑深隨著射流軸向傾角的增加而減小。
從圖10c可得,隨著射流軸向傾角的增大,巖石表面坑徑不斷增大。因此為了擴大巖石表面的破碎面積,合理選擇射流軸向傾角十分必要。
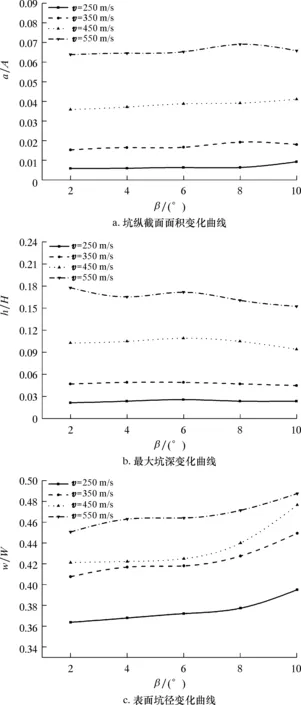
圖10 不同射流軸向傾角下巖石破損坑 指標變化曲線(t=0.05 ms)Fig.10 Variation of rock damage pit index under different jet axial inclinations (t=0.05 ms)
5 結 論
(1)基于SPH方法構建了組合射流沖蝕巖石的數值模型,通過模擬分析組合射流沖擊巖石的動態損傷過程,并與已有研究結果對比,驗證了所建模型的有效性。
(2)射流噴距對組合射流破巖能力有著顯著影響,破巖效果隨著射流噴距的增加而先增大后減小,在本文研究范圍內,最優噴距范圍為3~5 mm。
(3)射流直徑的改變會直接影響巖石破損坑形狀,隨著射流直徑的增大,巖石破損坑縱截面面積不斷增大,同時破損坑底部的凸臺逐漸消失。
(4)射流軸向傾角會顯著影響巖石表面破損情況,隨著射流軸向傾角的增加,巖石破損坑縱截面面積變化較小,表面坑徑不斷增大。

