基于分時電價的電動汽車充電負荷引導方案

韓秉乾，劉 敏

（貴州大學 電氣工程學院，貴州 貴陽 550025）

0 引言

國家發改委2020年發布《關于擴大戰略性新興產業投資培育壯大新增長點增長極的指導意見》，鼓勵打造基于城市信息模型、融合城市動態和靜態數據于一體的“車城網”平臺，推動智能汽車與智慧城市協同發展[1]。電動汽車憑借清潔、無污染、高性能以及具有優惠政策扶持等優勢，逐漸成為新世紀汽車產業推廣和技術變革的主流[2]。大量基礎設施組成的充電網絡不僅可以方便電動汽車按需充電的行為，而且也將有效降低車主的里程焦慮。

受生活習慣和出行習慣的影響，電動汽車車主更喜歡在負荷高峰時接入電網[3]。以居住區為例，大約有 82%的電動汽車車主下班后選擇到達居民區后充電，于是電動汽車充電負荷和居民區負荷一起形成了典型的“鴨子曲線”[4]，造成了居民區負荷分布不均衡的現象。由于公用事業單位不能拒絕用戶的用電需求[5]，故其在應對不均衡分布的負荷入網可能帶來的過壓和頻率問題[6]時就需要更大容量機組來平衡供需關系。電網中不均衡負荷的出現會導致部分機組的頻繁啟停，機組不能進行低成本的平穩操作[7]。不均衡分布的負荷提高了機組的運營成本，造成了產能浪費。

當前對負荷的引導策略是：根據路況、距離、時間和電價等因素，引導電動汽車選擇充電成本更低、充電樁資源更豐富的充電站。文獻[8]根據道路信息和電網充電信息為電動汽車提供導航服務，使得充電站資源得到有效分配，交通系統運行狀況得到改善。文獻[9]通過分析出租車群體時間成本、電力成本，為出租車推薦滿意度最大的充電站位置。在消費者效用最大化的目標下，該文獻利用離散選擇模型分析電動汽車車主的出行選擇和充放電選擇，但僅僅考慮工作和居住等程序性需求，對娛樂購物等目標性需求未做深入研究。

電價是一項重要的需求響應工具。在負荷引導中設計合理的電價會產生好的負荷引導效果。電價設計的 3種方式[7]包括：電力消費定價，分時電價和區域定價。

基于電力消費的定價方式對用戶便利度不夠，與市場融合度不高，不利于形成長期的電價機制[4]；分時電價主要受負荷需求影響，且研究成熟、應用廣泛；區域定價有利于區域協調，避免充電阻塞和資源浪費的情況，適用于大型區域間的電價設計。

文獻[7]融合分時電價和區域定價的特點，基于需求價格模型進行電價設計，引導電動汽車向充電樁資源豐富的充電站轉移，協調了不同區域的充電站利用率；但該文獻以線性表達式描述需求關系存在一定局限性，且不同電動汽車車主改變充電行為的閾值存在較大差異。文獻[10]在大城市功能分區和電動汽車用戶具有同質性的前提下，分析了用戶的充電決策；但該文獻僅分析工作和居家的程序性要求，未考慮娛樂目標性要求。文獻[11]結合旅行時間指數來確定各個路段的權重，通過調節充電服務費改善耦合路–電網絡整體運行狀態。

運輸系統與電力系統之間相互配合可以減小用戶成本，增加社會福利[12]。文獻[5]建立協調動態電價模型，減少了電動汽車充電負荷與居住地負荷的重疊，降低了電網問題發生的風險；但該文獻考慮范圍僅僅限于城市某一區域，缺乏城市功能性分區的整體視角。文獻[13]為充電站建立雙層動態隊列，以動態需求函數描述整體負荷水平，平衡了多個充電站的服務強度。文獻[14]建立了基于轉移矩陣的電價響應模型，但該模型適用于電動汽車群體而不適用于個體，所以有必要對電動汽車用戶個體的充電方案進行研究。

此外，無線充電技術[15]的快速發展也使得電網對電動汽車個體的充電調度方案更加靈活。

針對以上相關研究中存在的不足，本文提出以下改進方案：（1）將出行鏈和城市功能分區配合，以彌補當前諸多研究中忽視功能分區和對娛樂購物等目標性需求的情況。（2）運用 logit概率選擇模型的方法，解決不同車主行為改變的閾值存在差異的問題。（3）提出混合模式的出行鏈充電方案選擇，研究各個電動汽車用戶的電價響應行為，解決基于轉移矩陣的電價模型只適用于群體研究的問題。

1 整體方案

整體框架如圖1所示。首先根據城市道路信息建立城市路阻模型，并結合統計數據、出行鏈和最短路徑算法得到私家車用戶的出行信息；然后將一天一充和一天多充的充電模式選擇統一的充電方案選擇，并結合電價、用戶感知和選擇概率等得到最小化各充電站的日充電量波動和日充電負荷功率波動的充電負荷時空分布。

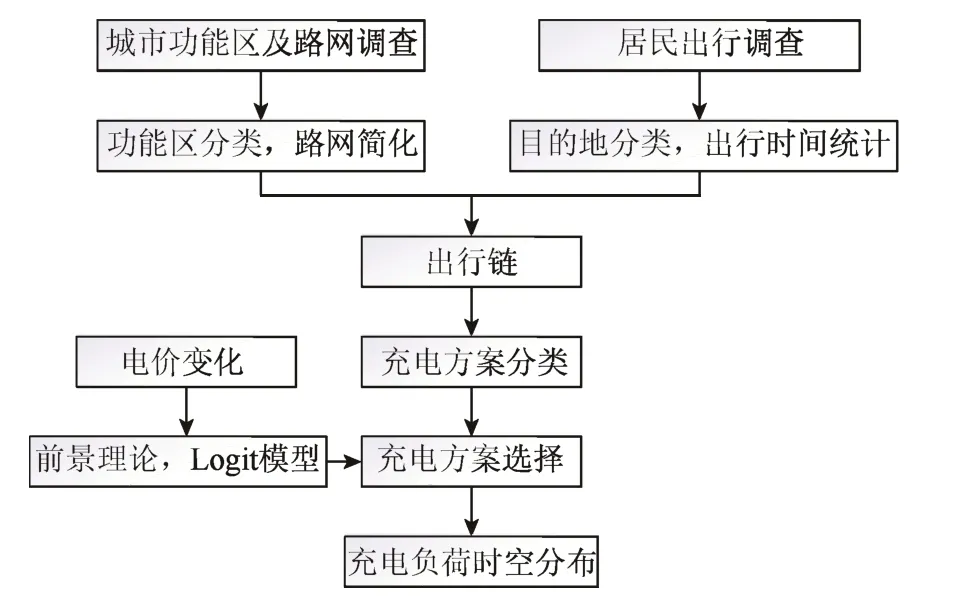
圖1 整體框架Fig. 1 The overall framework

2 交通道路模型

2.1 道路拓撲圖

路網模型是研究電動汽車時空變化的基礎。用圖論方法對城市路網中交通節點和交通路段進行描述[8]。

式中：G表示交通路網；V是交通網中所有交通節點的集合；E是交通網中所有交通路段的集合；W是各個路段總路阻的集合；a和b表示交通路網中有直接路段相連的2個節點。

式中：Tab表示路網中有直接交通路段相連的2個節點之間的路阻。

2.2 路阻函數模型

在城市交通網中，受道路等級和紅綠燈時間等因素的影響，車輛行駛速度受到限制。各路段花費總時間表示為：

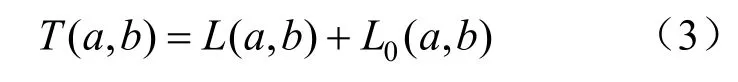
式中：L(a,b)表示各行駛路段的延誤時間；L0(a,b)表示各個行駛路段零流下的通行時間。

路段延誤時間[8]主要受到交通車流和道路長度的影響，可通過下式表示：

式中：L0表示各路段自由流下的行駛時間；c1，c2，c3，c4表示不同道路等級下的自適應系數；qab表示道路流量；Cab表示道路通行能力。

式中：M(a,b)是節點a和b之間路段的長度；V0(a,b)表示節點a和b之間路段的零流速度。

2.3 路徑選擇

由A地到B地的所有路徑可以表示為AB1，AB2，···。每一個路徑時間的權值可以表示為該路段包含所有路段的權值之和。

式中：r表示各條路徑所對應的節點序號；R表示每條路徑所包含的節點總數；w(vr–1,vr)表示路段通行時間權值。

假設電動汽車車主以行駛時間最短為目標來選擇最優路徑，則定義最短時間路徑：

3 車輛時空模型

電動汽車作為一種交通工具，其最重要的目的就是滿足電動汽車用戶的出行需求；所以本文以出行鏈來描述電動汽車的出行時空模型。

3.1 出行鏈結構

出行鏈包含了電動汽車車主一天之中的出行活動數量、時間順序等相關信息[16]，是對車輛一天信息的完整表達。私家車的行程目的地可分為3類：家（H），工作場所（W），其他（E）。將出行鏈選擇分為：住宅區–工作區–住宅區（H-W-H）、住宅區–其他–住宅區（H-E-H）、住宅區–其他–工作區–住宅區（H-E-W-H）、住宅區–工作區–其他–住宅區（H-W-E-H）。出行鏈結構[16]如下圖所示：

圖2 以家為起訖點的出行鏈結構Fig. 2 Trip chains structure with home as the starting and ending point

3.2 出行時刻分析

對于出行鏈 H-W-H第一個行程開始時間和第二個行程開始時間，采用美國國家公路交通安全管理局NHTS2009（National Household Travel Survey 2009）的車輛出行統計數據[17]分析用戶出行規律，表達式如下：

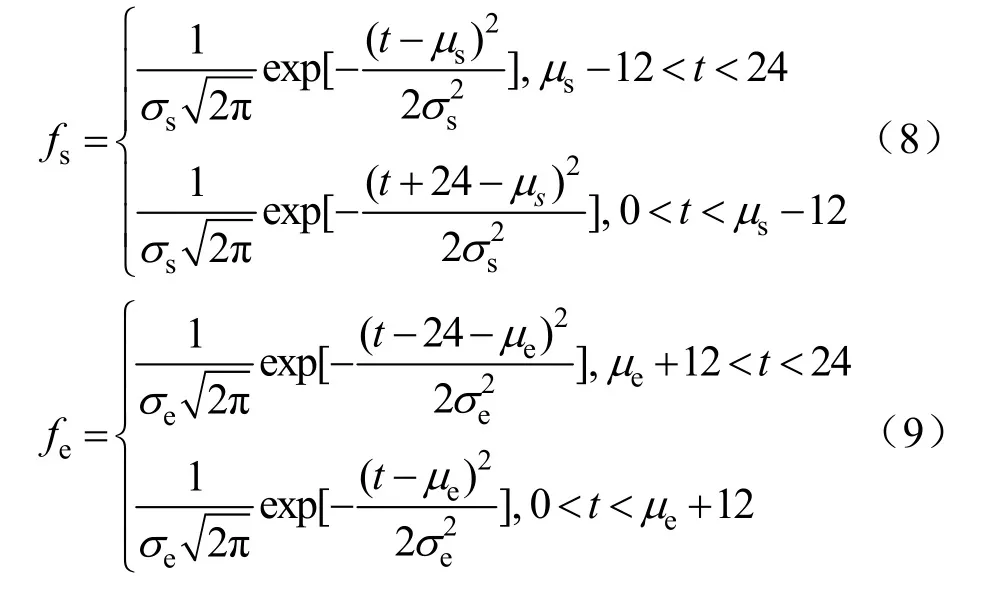
式中：μs和μe分別是進站時間和出站時間的期望；σs和σe分別是進站時間和出站時間的標準差。

由于工作日的上班時間相對固定，故出行鏈H-E-W-H第三個行程起始時間與出行鏈 H-W-H第二個行程開始時間相同，第二個行程起始時間與出行鏈 H-W-H第一個行程開始時間相同；同理，出行鏈H-W-E-H第一個行程起始時間與出行鏈H-W-H第一個行程開始時間相同，第二個行程起始時間與出行鏈 H-W-H第二個行程開始時間相同。

在休息日出行的私家車約占電動汽車總保有量的 70%，其主要行程為住宅區–其他–住宅區（H-E-H）[16]。

3.3 出行鏈充電決策分類

文獻[14]以轉移矩陣建立的價格響應模型僅適用于電動汽車群，不利于研究單一的電動汽車的充電選擇模型；故本文使用出行鏈充電決策分類來研究單個電動汽車的充電選擇情況。

3.3.1 一天多充模式

假設：電動汽車從住宅區出發。在出行鏈第一個行程，荷電狀態為0.9；結束出行鏈最后一段行程回到住宅區，充電到荷電狀態為0.9。

在出行鏈中任意行程中的停留點，電動汽車車主均可以考慮進行充電或者不充電。本文以集合的方式來表達一條出行鏈中的車主選擇方案。比如，用（0,1,1）表示復雜鏈“住宅區–其他–工作區–住宅區（H-E-W-H）”的充電選擇方案時，其表達的意思是：在結束出行鏈的第一個行程后，在娛樂休閑區停留時不充電；在結束出行鏈的第二個行程后，在工作區停留時選擇充電；在結束出行鏈的第三個行程后，即回到居住區時選擇充電。

由以上假設和規定，可以得到具體決策方案，如表1所示。

表1 各出行鏈的決策方案Tab. 1 Decision-making plans of each trip chain

由表1可知，簡單出行鏈有2個充電決策方案，復雜出行鏈有4個充電決策方案。

3.3.2 一天一充模式

由于車主在居住區和工作區停留時間較長，在休閑娛樂區停留時間較短，故一天一充只發生在工作區或者居民區。一天一充的決策方案如表2所示。

表2 一天一充出行鏈決策方案Tab. 2 Decision-making plans of daily charging trip chain

由表2可知，一天一充模式下，簡單出行鏈有2個充電決策方案，復雜出行鏈有2個充電決策方案。

3.3.3 混合充電模式

電動汽車車主可能選擇一天多充模式和一天一充模式。混合模式下，各個出行鏈的出行方案如表3所示。

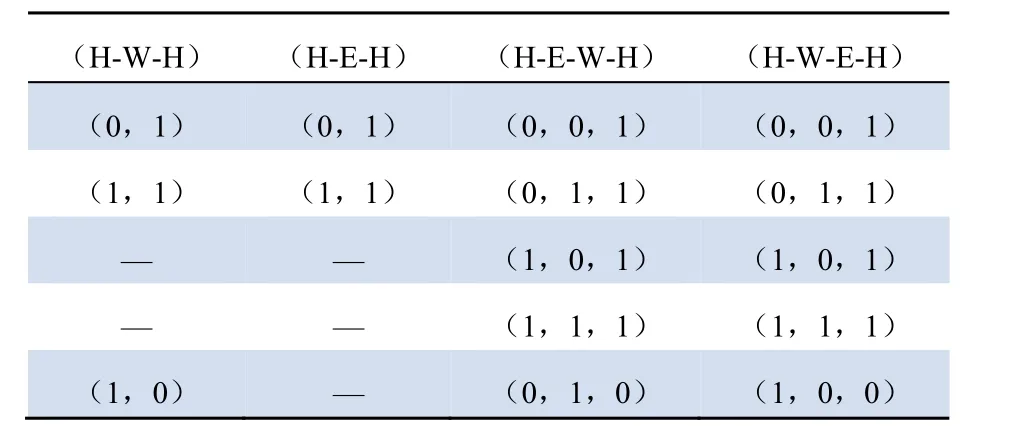
表3 混合充電模式下出行鏈決策方案Tab. 3 Decision-making plans of trip chain under hybrid charging condition

由表3可知，混合充電模式下，簡單出行鏈有2個或3個充電決策方案，復雜出行鏈有5個充電決策方案。

利用充電模式建立電動汽車負荷，并構建時間段數–充電站數的二維矩陣以表示第n輛電動汽車在第k個充電決策的充電負荷。

4 前景理論

前景理論[18]是一種考慮決策者個體感知的決策方法。在不確定方案選擇的情況下：傳統效用函數理論認為用戶個體心理特質和行為特征的變化僅受實際方案效用的影響；前景理論認為用戶個體心理特質和行為特征的變化受實際方案和參考方案效用偏離程度的影響。

相較于電價設計中將用戶個體假設為完全理性狀態的傳統效用函數理論，前景理論中的價值函數更能反映價格因素對個體非理性的主觀價值感受期望的影響。前景理論的價值函數以冪函數形式表示：

式中：Δa表示某個決策偏離參考決策的大小；α和β為敏感度的參數，表征價值函數的凹凸程度；λ表示損失厭惡程度，一般取值大于0。

本文將當地的分時電價作為參考決策電價。決策方案的偏離程度，主要由決策電價與參考電價之差決定。某個決策方案和參考決策方案偏離程度可表示為：

式中：T表示所有時間段；Prt表示某個決策方案中的電價；P0t表示參考方案中的電價；Pe表示充電功率。

5 Logit概率選擇模型

Logit模型[19]是一種離散選擇模型，用于決策者根據不同方案的效用選擇合適的方案。

電動汽車用戶選擇充電方案是一項不確定事件，除充電費用影響充電方案選擇外，用戶的偶然事件也會影響充電方案選擇。當電價變化后，用電動汽車車主的各個決策的價值函數值得到各個決策的選擇概率，表達式如下：

式中：g表示充電決策方案序號；G表示單一電動汽車所有決策方案的數量；E(Δa)表示前景理論的價值函數。

6 電動汽車負荷模型構建

6.1 目標函數

從城市角度來看，各個充電站充電量反映充電站的工作強度。均衡充電量有助于平衡各充電站的工作強度。從單個充電站角度來看，均衡不同時刻的充電功率有利于增加充電設備平均利用率，減小充電站初始投資。

將各個充電站充電量的波動和各個充電站的負荷功率波動的和作為總的目標函數，將分時電價作為優化變量，構建分時電價模型。

式中：Png表示第n輛電動汽車，第g個充電決策的選擇概率；表示第n輛電動汽車，第g個充電決策的充電負荷在m號充電站和各個時間段的分布情況；Prt表示t時間段的實際電價；P0t表示t時間段的參考電價；Δang表示某一充電決策方案的實際電價與參考電價之差。Pen表示第n輛電動汽車日負荷，等于第n輛電動汽車所有充電決策方案的選擇概率與相應充電負荷乘積的和。

6.2 約束條件

6.2.1 電價約束

設置電價的上界和下界；同時，為防止定價僅考慮單方面經濟利益，所有時間段充電價格平均值保持不變[20]。

式中：Prtmax表示電價上限；Prtmin表示電價下限。

6.2.2 荷電狀態約束

電動汽車電池實際儲存的電量不高于容量，不小于0。

式中：SOC表示電池荷電狀態。

6.3 算法

粒子群算法[21]是一種廣泛運用于模型求解的啟發式算法。本文以最小化各充電站的日充電量波動和日充電負荷功率波動為目標，將電價作為粒子群算法的粒子進行求解。

7 算例分析

7.1 算例條件

以文獻[22]中16個節點、24條路的交通路網表示某典型城區路網情況。交通路網中的節點與功能分區如表4所示。

表4 節點與功能區Tab. 4 Nodes and functional areas

抽象的交通路網分布情況如圖3所示。

圖3 交通網路抽像圖Fig. 3 Traffic network image

各路段長度設置如表5所示。

表5 各路段長度Tab. 5 Length of each section km

電動汽車數據設置如下：電池容量24 kW·h，慢充充電功率為3.3 kW，快充充電功率為6.5 kW，每km耗電量0.225 kW·h；在居住區和工作區采用慢充，在娛樂區采用快充。根據文獻[18]，設置風險偏好系數α=0.88，風險規避系數β=0.88，損失厭惡程度λ=1.25。路阻函數參數設置參考文獻[23]。工作日各出行鏈車輛設置為200輛，非工作日出行鏈車輛設置為420輛。

工作日出行的車輛在其他區域的停留時間滿足1 h～2 h的均勻分布，休息日出行的車輛在其他區域的停留時間滿足1 h～5 h的均勻分布。在休息日的出行車輛中，50%的私家車出行時間滿足μ=8.92、σ=3.24的正態分布，其余50%的私家車出行時間滿足μ=16.47、σ=3.41的正態分布[16]。

電網在該居民區的分時電價和時段劃分[24]如表6所示。

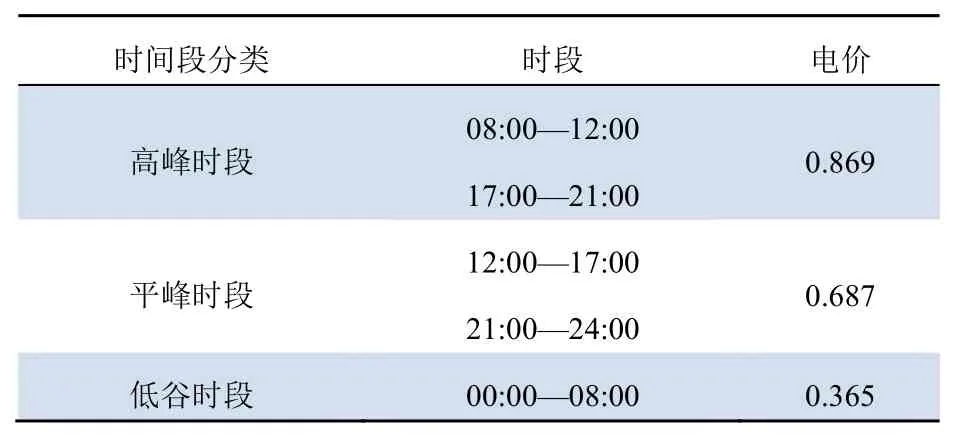
表6 電價和時間段劃分Tab. 6 Electricity price and time period division 元/kW·h

7.2 算例分析

7.2.1 單一電動汽車

以本例中出行鏈為H-W-E-H的43號電動汽車為例，分析充電選擇情況。

由3.2小節可知，該電動汽車有5種充電方案，各個充電方案的負荷功率如圖4所示。

圖4 電動汽車的5種充電決策方案Fig. 4 Five charging decision-making schemes for electric vehicles

如圖4所示：方案1表示43號電動汽車在家充電的情況；方案2表示43號電動汽車結束W-E行程后在娛樂區充電，然后結束E-H行程回到家再次充電的情況；方案3表示43號電動汽車結束H-W行程后在工作區充電，然后結束E-H行程回到家再次充電的情況；方案4表示43號電動汽車結束H-W行程、W-E行程和E-H行程后分別在工作區、娛樂區和住宅區充電的情況；方案5表示43號電動汽車在家充電的情況。以上5個充電方案代表了出行鏈為H-W-E-H的電動汽車的全部充電決策方案。

根據充電方案的電費，結合前景效用函數和logit模型，得到各個充電方案選擇概率如表7所示。

表7 充電決策方案選擇概率Tab. 7 Probability of selection of charging decision schemes

將43號電動汽車各充電決策方案的充電負荷乘以選擇概率，然后相加得到該電動汽車每日的綜合充電負荷，43號電動汽車為出行鏈為 H-W-E-H的電動汽車代表，反映了該類電動汽車的日負荷分布情況。如圖5所示。

圖5 電動汽車每日充電負荷Fig. 5 Daily charging load of electric vehicles

7.2.2 3種充電模式分析

在前景理論的背景下，以5個典型工作日和2個典型休息日構建一周中某一天的3種分時電價模型，得到一天一充模式、一天多充模式和混合充電模式這3種充電模式的充電站充電量波動和充電功率波動情況，具體如表8所示。

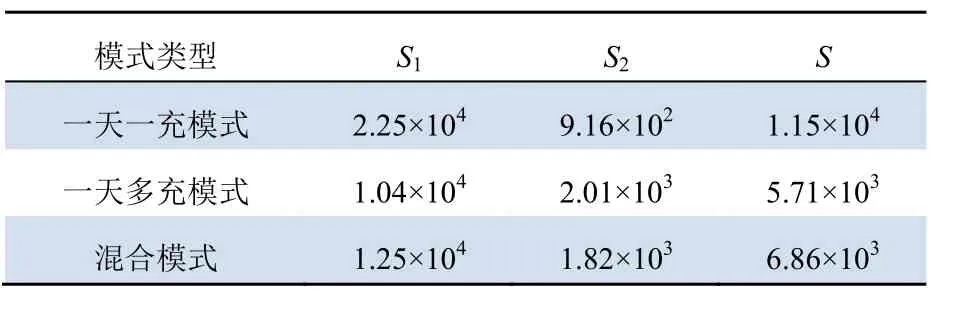
表8 3種充電模式下充電站充電量波動和充電功率波動Tab. 8 Charging capacity fluctuation and charging power fluctuation of charging stations under three charging modes

由表8可知：一天多充模式在S1列的數值最小，說明該充電模式在平衡各個充電站的充電量波動上的能力高于其他充電模式。一天一充模式在S2列的數值最小，說明該充電模式在平衡各個充電站的充電負荷功率波動上的能力高于其他充電模式。使用混合充電模式時，S1列的數值小于一天一充模式，S2的數值小于一天多充模式；這說明該充電模式有效融合了一天一充模式和一天多充模式的優點。

3種充電模式的電動汽車充電負荷分布情況如圖6所示。

圖6 各個充電模式下的總負荷曲線Fig. 6 The total load curve in each charging mode

由圖6可知：一天一充模式下，電動汽車在居民區負荷較低；一天多充模式下，電動汽車在居民區負荷較高。2種模式均未合理利用居民區的充電設施。混合充電模式平衡了居民區過高或過低的充電負荷。

7.2.3 區域充電負荷分布

假設常規情況下，70%的電動汽車車主選擇在家充電[25]，30%車主選擇在工作地充電。該情況下的電動汽車充電負荷分布如圖7所示。

圖7 常規情況下充電負荷分布Fig. 7 Load distribution under normal conditions

由圖7可知，常規情況下的充電負荷集中于居民區，工作地充電設施未充分利用。

在分時電價引導負荷的情況下，電動汽車車主根據電動汽車的充電費用選取充電方案。本算例選取表6的分時電價作為參考方案，以5個典型工作日和2個典型休息日構建一周中某一天基于logit模型的前景理論分時電價模型，實現對城市負荷進行引導。該情況下的電動汽車充電負荷分布如圖8所示。

圖8 混合模式下的各區域負荷Fig. 8 The load of each area in the mixed mode

由圖8可知，分時電價引導情況下的充電負荷不只集中于居民區，工作區負荷的增加使得工作區充電設施得到充分利用。此外，娛樂區的充電負荷升高也降低了居民區的負荷。由于電動汽車在娛樂區停留時間較短，故娛樂區域充電對負荷的調節能力有限。娛樂區充電也是造成圖6中混合模式下負荷曲線第二個波峰時間提前的主要原因。

8 結論

本文主要研究了基于分時電價設計的電動汽車充電負荷引導方案。算例分析結果表明，本方案可以起到降低充電站充電量波動和充電功率波動的作用。

由于本文的分時電價時間段劃分直接使用電網的時間段，未緊密結合電動汽車的負荷特點，故今后研究將結合電動汽車負荷特點進一步完善對各時間段的劃分。