透析洛倫茲力沖量的應(yīng)用

安徽 徐建強(qiáng) 崔北元

疊加場作用下物體的非勻變速直線運(yùn)動(dòng)、曲線運(yùn)動(dòng)問題以及并列電磁場下的多解問題是學(xué)生復(fù)習(xí)過程中的難點(diǎn)，本文從物理觀念的本質(zhì)出發(fā)，通過模型建構(gòu)推導(dǎo)洛倫茲力沖量表達(dá)式，巧妙解答此類問題，深化學(xué)生對物理觀念的理解。

一、推導(dǎo)洛倫茲力沖量公式

1.構(gòu)建情境

如圖1所示，空間中存在垂直于紙面向里的勻強(qiáng)磁場，磁感應(yīng)強(qiáng)度為B，一電荷量為q、質(zhì)量為m的帶正電粒子以初速度v0垂直于磁場進(jìn)入勻強(qiáng)磁場中，僅在洛倫茲力作用下做勻速圓周運(yùn)動(dòng)，運(yùn)動(dòng)一段時(shí)間后速度變?yōu)関，把帶電粒子的速度和洛倫茲力進(jìn)行正交分解，分別以vx0、vx為初速度和末速度沿x軸方向的分量，分別以vy0、vy為初速度和末速度沿y軸方向的分量，任意時(shí)刻帶電粒子所受洛倫茲力F在x軸和y軸方向的分量分別為Fx、Fy。

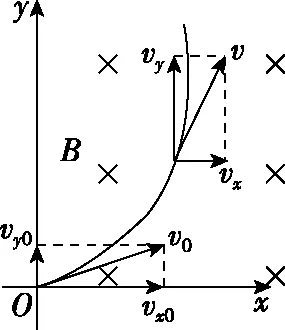
圖1

2.微元積累法推導(dǎo)

分析粒子在x軸方向的運(yùn)動(dòng)，取很小一段時(shí)間Δt內(nèi)x軸方向的速度變化量為Δvx；由左手定則可知x軸方向的洛倫茲力僅由y軸方向的速度分量vy決定，其大小為Fx=qvyB。

由動(dòng)量定理有-qvyBΔt=mΔvx(負(fù)號(hào)表示洛倫茲力與vx0方向相反)，其中vyΔt=Δy

兩邊求和有-qB∑vyΔt=m∑Δvx，其中∑vyΔt=y，∑Δvx=vx-vx0

得qBy=mvx-mvx0

同理可得qBx=mvy-mvy0

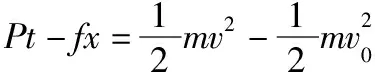
二、典例剖析

1.并列場作用下運(yùn)動(dòng)問題

【例1】現(xiàn)代科學(xué)儀器常利用電場、磁場控制帶電粒子的運(yùn)動(dòng)。在真空中存在著如圖2所示的多層緊密相鄰的勻強(qiáng)電場和勻強(qiáng)磁場，電場和磁場的寬度均為d。電場強(qiáng)度為E，方向水平向右；磁感應(yīng)強(qiáng)度為B，方向垂直紙面向里。電場、磁場的邊界互相平行，一個(gè)質(zhì)量為m、電荷量為q(q>0)的粒子在第1層電場左側(cè)邊界某處由靜止釋放，粒子始終在電場、磁場中運(yùn)動(dòng)，不計(jì)粒子重力及運(yùn)動(dòng)時(shí)的電磁輻射。

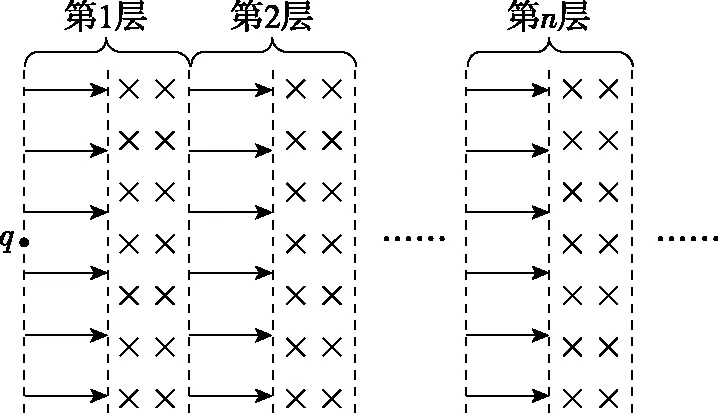
圖2

(1)求粒子在第2層磁場中運(yùn)動(dòng)時(shí)速度v2的大小與軌跡半徑r2。

(2)粒子從第n層磁場右側(cè)邊界穿出時(shí)，速度的方向與水平方向的夾角為θn，試求sinθn。

(3)若粒子恰好不能從第n層磁場右側(cè)邊界穿出，試問在其他條件不變的情況下，也進(jìn)入第n層磁場，但比荷較該粒子大的粒子能否穿出該層磁場右側(cè)邊界，請簡要推理說明。

【分析】(1)粒子在第2層進(jìn)入磁場時(shí)已經(jīng)經(jīng)歷兩次電場加速，由動(dòng)能定理可求得進(jìn)入第2層時(shí)的速度，再由洛倫茲力提供向心力即可求得軌跡半徑；(2)粒子在整個(gè)運(yùn)動(dòng)過程中，水平方向的電場力改變速度的大小，豎直方向僅受因?yàn)樗椒炙俣犬a(chǎn)生的洛倫茲力，該力引起豎直方向速度的變化，故可以利用洛倫茲力沖量公式找到豎直分速度，利用電場力做功求出末速度，從而解答該問。(3)粒子不能從第n層磁場右側(cè)邊界穿出即粒子到達(dá)右側(cè)邊界時(shí)速度恰好豎直向上，仍可利用洛倫茲力的沖量公式求出寬度d與粒子比荷的關(guān)系進(jìn)而求解。

【解析】(1)粒子在進(jìn)入第2層磁場時(shí)，經(jīng)過兩次加速，中間穿過磁場時(shí)洛倫茲力不做功

粒子在第2層磁場中受到的洛倫茲力提供向心力

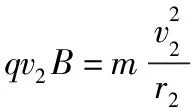
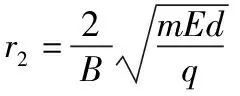
(2)設(shè)帶電粒子從第n層磁場右邊界穿出時(shí)速度為vn，豎直方向分速度為vny，如圖3所示，帶電粒子在豎直方向只受洛倫茲力，洛倫茲力在豎直方向上的沖量與粒子在磁場中水平方向的位移nd成正比，由動(dòng)量定理得

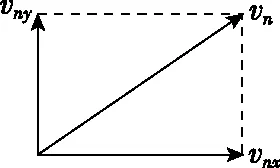
圖3

qBnd=mvny-0

帶電粒子運(yùn)動(dòng)過程中只有電場力做功，由動(dòng)能定理得

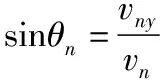
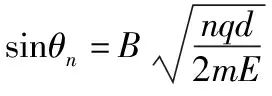
(3)若粒子恰好不能從第n層磁場右側(cè)邊界穿出，則粒子到第n層磁場右側(cè)時(shí)速度方向恰好豎直向上，設(shè)其速度為vn0，分別從開始到第n層磁場右側(cè)由動(dòng)能定理和豎直方向上的動(dòng)量定理得

qBnd=mvn0-0

【點(diǎn)評】本題考查帶電粒子在組合場中的運(yùn)動(dòng)，在處理后兩問時(shí)很容易想到借鑒第(1)問的處理思想，根據(jù)電場力做功明確末速度，再根據(jù)洛倫茲力充當(dāng)向心力找出第n層磁場中的半徑關(guān)系，由等差數(shù)列規(guī)律得出通項(xiàng)式，即可求出sinθn，這是傳統(tǒng)參考答案給出的復(fù)雜解法(在此不再贅述)，這種解法要求學(xué)生能正確分析物理過程，并能靈活應(yīng)用數(shù)學(xué)知識(shí)，難度較大，對學(xué)生綜合素養(yǎng)要求極高。但采用的洛倫茲力沖量法大大簡化了解題過程，免去了分析運(yùn)動(dòng)細(xì)節(jié)找圓心、半徑及幾何關(guān)系等困難，起到高效解題的效果，針對這類并列場問題此法值得推薦給考生學(xué)習(xí)。

2.疊加場作用下滾輪線問題

【例2】如圖4所示，空間存在范圍足夠大的垂直于xOy平面向外的勻強(qiáng)磁場和沿y軸正方向的勻強(qiáng)電場，磁感應(yīng)強(qiáng)度大小為B，電場強(qiáng)度大小為E。讓質(zhì)量為m，電荷量為q(q>0)的粒子從O點(diǎn)以初速度v0沿y軸正方向發(fā)射。研究表明，粒子在xOy平面內(nèi)做周期性運(yùn)動(dòng)，且在任一時(shí)刻，粒子速度的x分量vx與其所在位置的y坐標(biāo)成正比，比例系數(shù)與電場強(qiáng)度E大小無關(guān)。不計(jì)重力和粒子間的影響，求：

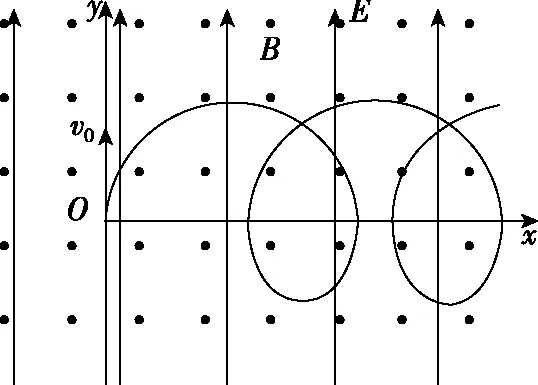
圖4

(1)該粒子運(yùn)動(dòng)過程中速度的最大值vm；

(2)當(dāng)粒子運(yùn)動(dòng)速度達(dá)到最大時(shí)，粒子距x軸的距離。

【分析】電場力改變速度大小，洛倫茲力改變速度方向，當(dāng)速度最大時(shí)即電場力做功最多，結(jié)合洛倫茲力的作用可知此時(shí)速度方向水平，在整個(gè)運(yùn)動(dòng)過程中粒子水平方向只受因豎直方向分速度產(chǎn)生的洛倫茲力影響，故可列出該粒子在水平方向上的動(dòng)量定理表達(dá)式進(jìn)行求解。

【解析】粒子運(yùn)動(dòng)到最高點(diǎn)，其速度最大并且方向沿x軸，對粒子由x軸方向的動(dòng)量定理有

qBy=mvm-0

從O點(diǎn)到最高點(diǎn)只有電場力做功，由動(dòng)能定理有

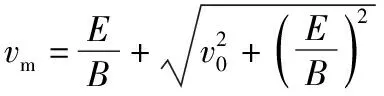
【點(diǎn)評】(1)該解法從洛倫茲力和電場力的作用特點(diǎn)出發(fā)，利用動(dòng)量定理、動(dòng)能定理進(jìn)行求解，有效避免出現(xiàn)題干中理解vx與其所在位置的y坐標(biāo)成正比，比例系數(shù)與電場強(qiáng)度E大小無關(guān)的思維難度。教學(xué)中還可以改編問題，若已知粒子第一次速度達(dá)到最大所用的時(shí)間，則還可以利用水平方向動(dòng)量定理求解水平方向位移，從而提升學(xué)生思維能力。

圖5

3.拓展應(yīng)用——磁約束下非勻變速直線運(yùn)動(dòng)問題

【例3】如圖6所示，空間有一個(gè)范圍足夠大的勻強(qiáng)磁場，磁感應(yīng)強(qiáng)度為B，將一個(gè)質(zhì)量為m、電荷量為+q的帶電小圓環(huán)套在一根固定的絕緣豎直細(xì)桿上，桿足夠長，環(huán)與桿之間的動(dòng)摩擦因數(shù)為μ。現(xiàn)使圓環(huán)以初速度v0向上運(yùn)動(dòng)，經(jīng)時(shí)間t圓環(huán)回到出發(fā)位置。不計(jì)空氣阻力。已知重力加速度為g。求當(dāng)圓環(huán)回到出發(fā)位置時(shí)速度v的大小。

圖6

【分析】圓環(huán)在沿桿運(yùn)動(dòng)過程中對其受力分析可知，上升階段速度減小導(dǎo)致洛倫茲力減小，而所受摩擦力與洛倫茲力成正比，故為非勻變速直線運(yùn)動(dòng)，下降亦是如此。由于已知運(yùn)動(dòng)總時(shí)間，則可以嘗試?yán)脛?dòng)量定理求解速度，不難發(fā)現(xiàn)摩擦力的沖量為μqBy，y為豎直方向的位移，全程位移為零從而有效消除摩擦力的沖量，進(jìn)而解答題目。

【解析】在圓環(huán)運(yùn)動(dòng)的過程中，圓環(huán)受向下的重力mg、水平方向的洛倫茲力qvB、細(xì)桿的彈力FN和摩擦力f，其中f一直與運(yùn)動(dòng)方向相反，且摩擦力的大小f=μFN=μqvB。

圓環(huán)從開始向上運(yùn)動(dòng)到回到出發(fā)位置的過程中，取豎直向上為正方向，根據(jù)動(dòng)量定理有

If-mgt=-mv-mv0

而If=-∑μqv上BΔt上+∑μqv下BΔt下=μqB(x下-x上)=0

解得v=gt-v0