反艦飛行器單發命中概率飛行試驗檢驗的幾個關鍵問題研究*

鄭小兵 李 曦 劉文超 劉榮豐 紀凱夫

（中國人民解放軍91550部隊 大連 116084）

1 引言

反艦飛行器的命中精度通常使用單發飛行器在無故障飛行條件下命中目標的概率來表示，即單發命中概率。單發命中概率能夠綜合反映出飛行器的作戰使用性能，無論是定型試驗還是批檢試驗，反艦飛行器飛行試驗方案大多以單發命中概率作為主檢指標來進行設計。反艦飛行器的單發命中概率主要取決于目標指示誤差、目標機動誤差、平臺導航誤差、飛行導航誤差和飛行器導引誤差。靶場組織反艦飛行器發射飛行試驗受到發射條件、航區管道、靶船保障、安全控制和目指保障等一系列條件約束，影響單發命中概率的主要誤差源難以在飛行試驗中得到有效構設，導致單發命中概率這一指標很難在飛行試驗中得到實質性檢驗[1～2]。

隨著裝備試驗鑒定工作的新發展和裝備作戰使用提出的新要求，反艦飛行器單發命中概率檢驗工作呈現出了一些新問題。傳統的“N發M中”的單發命中概率檢驗方案在試驗方法和試驗實施均存在問題，難以對反艦飛行器單發命中概率進行科學準確的檢驗。飛行器命中區域的確定一直是研制方與檢驗方爭議的焦點，關于命中區域的側向判據和高度判據應針對不同試驗方案開展進一步的研究。在脫靶量測量設備無法獲取飛行器命中精度數據時，是否能夠利用遙測參數估算反艦飛行器命中精度是當前試驗結果分析中大家廣泛關注的一個工程實踐問題。

2 單發命中概率檢驗方法討論

2.1 傳統“N發M中”試驗方案設計

單發命中概率是反艦飛行器武器系統最重要的戰術技術指標之一，能夠比較全面地描述出武器系統的總體性能，并且指標值適中，易于試驗方案的設計，因此反艦飛行器飛行試驗方案設計往往圍繞該指標展開，基于二項分布經典假設檢驗方法進行單發命中概率指標的檢驗和飛行試驗方案的設計[3]。

原假設為H0：P=P0，P0為單發命中概率的設計指標。備擇假設為H1：P=P1，P1為單發命中概率的最低可接受值。由此可以計算檢出比λ和鑒別比d。

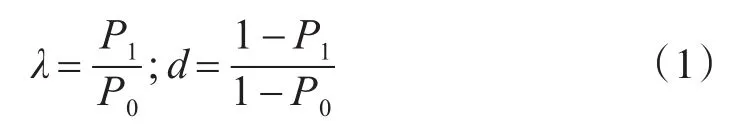
由試驗子樣N、檢出比λ和鑒別比d可以計算得到檢驗判決數K。

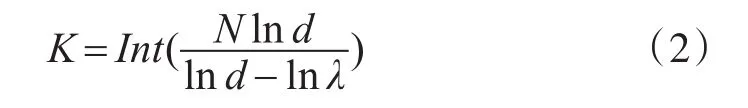
如果試驗成功數M大于K，接受原假設，否則拒絕原假設。由此制定的檢驗方案的生產方風險α和使用方風險β為

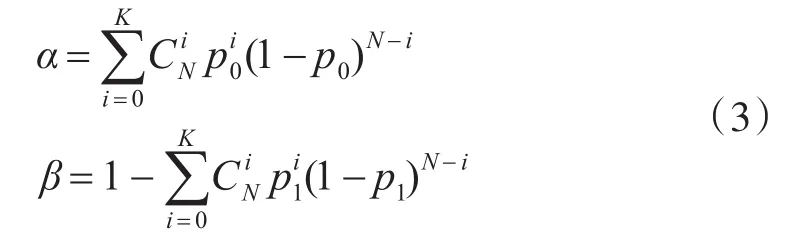
假定某飛行器單發命中概率指標為0.75，訂購方最低可接受值為0.54，則λ=0.72，d=1.84；可以求解出當N=7，M=5的時候，生產方風險α為0.2436，使用方風險β為0.2973。滿足生產方風險和使用方風險控制在0.3以下且生產方風險略低于使用方風險的設計原則。

2.2 單發命中概率誤差源分析

反艦飛行器的單發命中概率主要取決于飛行器飛行可靠度、目標捕捉概率和自導命中概率，飛行器的飛行可靠度是武器系統設計的固有特性，可以另行考慮。影響目標捕捉概率的誤差源又主要包括目標指示誤差、目標機動誤差、平臺導航誤差、飛行導航誤差和飛行器導引誤差。目標指示誤差由目標指示系統（衛星、預警機、艦載雷達等）測量誤差和信息傳輸時延誤差組成；目標機動誤差是指目標信息封裝后至飛行器捕獲目標前這段時間目標運動帶來的誤差；平臺導航誤差是指飛行器發射時平臺提供的發射點位置誤差；飛行導航誤差包括初始對準誤差和慣導漂移誤差。以某型飛行器為例，其單發命中概率的各誤差源影響分布如表1所示，出于保密考慮，表中數據進行了歸一化處理[5～6]。

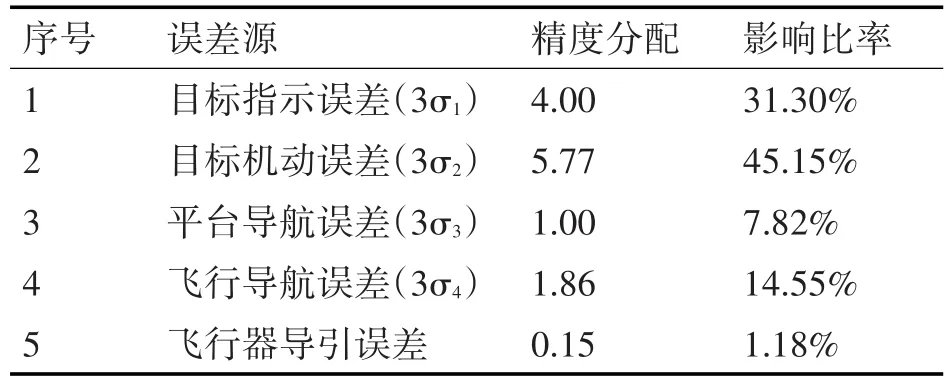
表1 單發命中概率誤差源影響分布

觀察表1可以看出，飛行器導引誤差對命中概率影響很小，尤其是末端超音速反艦巡航飛行器的突防速度和機動能力很強，在導引系統工作正常的情況下，典型目標擺脫飛行器攻擊的概率很小，飛行器發射飛行試驗和演習演練的結果也有效證實了這種情況。由此看來，在飛行器正常工作的情況下，單發命中概率主要取決于目標捕捉概率，各項誤差源對于目標捕捉概率的影響程度如圖1所示。

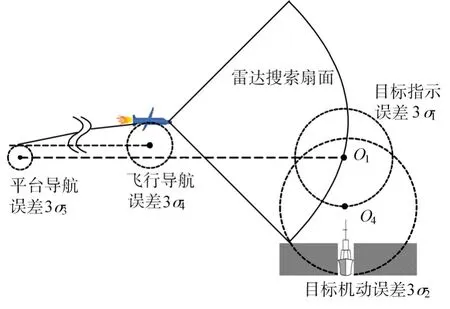
圖1 目標捕捉概率影響因素示意圖

圖中陰影部分表示導引頭搜索范圍不能覆蓋的區域，該區域所占比例加上飛行可靠度的影響共同決定了單發命中概率。

2.3 單發命中概率檢驗方法的主要問題

反艦飛行器性能鑒定試驗方案設計使用單發命中概率作為主要檢驗指標存在兩個方面的主要問題，一方面影響單發命中概率指標的主要誤差源在飛行試驗中難以得到有效構設，使得單發命中概率的檢驗流于形式；另一方面將單發命中概率指標當成設計值，通過鑒別比來調整最低可接受值的方法一直存在質疑。

以某型反艦飛行器設計定型飛行試驗為例，其影響單發命中概率的主要誤差源在性能鑒定飛行試驗中的表現如表2所示[7～8]。

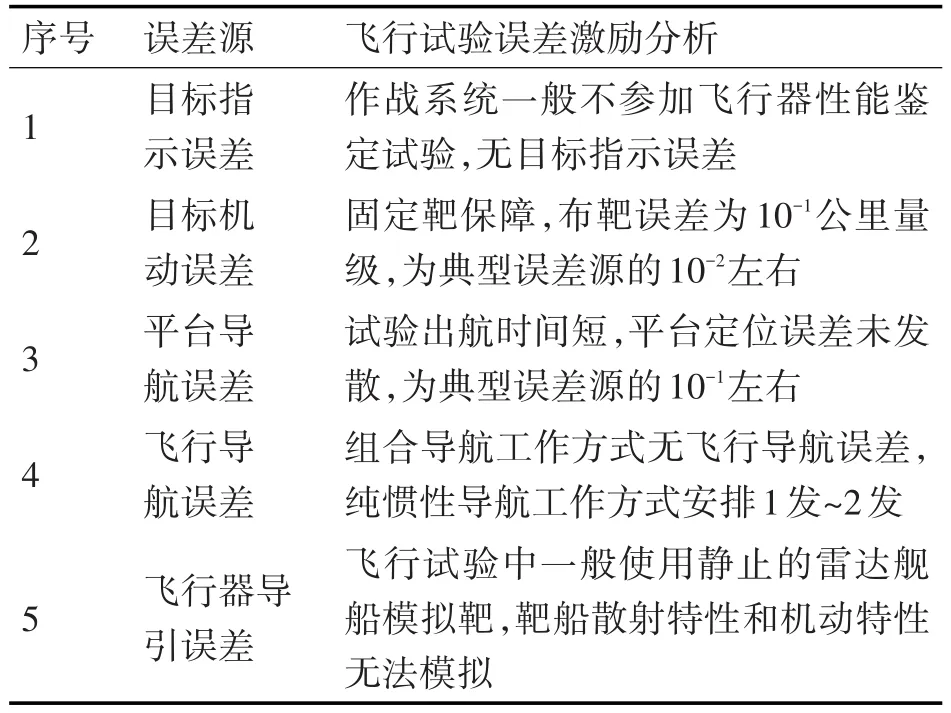
表2 單發命中概率誤差源激勵分析

綜合表2信息，可以看出在飛行試驗中影響單發命中概率的主要誤差源并不能有效達成，結合靶場近年來數十發反艦飛行器飛行試驗結果，“飛行正常即命中”基本形成共識。

2.1節中介紹的檢驗方案核心思想是將研制總要求規定的單發命中概率作為研制方需達到的規定值P0，通過鑒別比λ設計出使用方的最低可接受值P1。新發布的國軍標對最低可接受值的規定進行明確，認為研制總要求中應該明確指標的規定值和最低可接受值，如果僅規定一個值認為是最低可接受值。這樣傳統的“N發M中”的試驗檢驗方法的理論基礎就被推翻了。

綜合上述，對反艦飛行器單發命中概率飛行試驗檢驗方法提出以下幾點建議：

1）傳統的“N發M中”單發命中概率檢驗方案缺乏理論依據，且在實際飛行試驗中沒有構設出影響單發命中概率的主要誤差源，建議不再使用單發命中概率作為主檢指標進行飛行試驗設計；

2）單發命中概率指標可以使用理論分析和仿真試驗進行檢驗，并且在飛行試驗中盡可能多安排全系統試驗，充分激勵出影響單發命中概率的主要誤差源，對單發命中概率指標進行飛行試驗驗證；

3）在大多數飛行試驗中影響目標捕捉概率的主要誤差源沒有激勵出來，主要檢驗的是飛行器導引誤差，應該對該試驗條件下的命中精度進行更加細致的分析，尤其是命中區域應給出更加精準的描述。

3 反艦飛行器命中區域問題討論

3.1 傳統的反艦飛行器命中判別方法

GJB 3868-99中關于反艦飛行器的命中域是這樣定義的，根據典型目標的噸位、雷達有效反射面積和噪聲級別，定義命中域為以靶標反射體中心（近似等效反射中心）為中心，沿其艏艉線長±Lm、寬±Bm、高出水線Hm的長方體[9]。命中的判別公式為

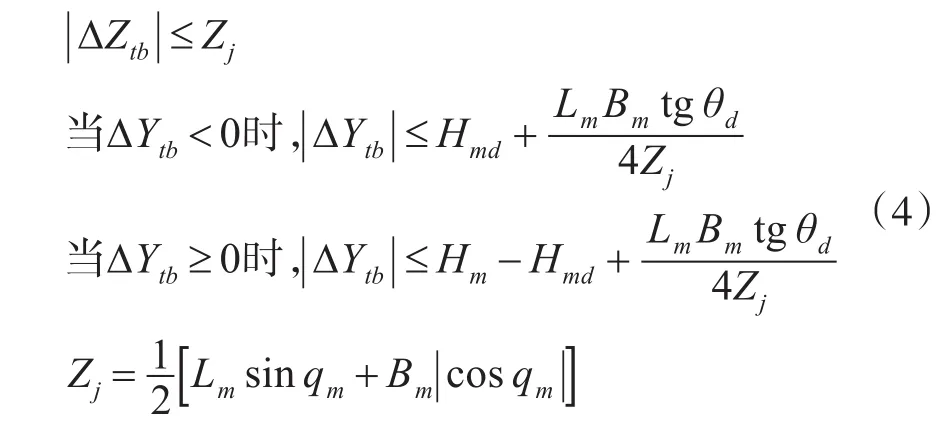
|ΔZtb|為側向脫靶量，ΔYtb為高度脫靶量，Lm、Bm、Hm為典型目標簡化長方體的長度、寬度和高度，Hmd為典型目標的等效模擬中心高度，qm為目標舷角，θd為與目標遭遇時彈道傾角的外測值。

分析以上描述，可以看出對于反艦飛行器攻擊大中型水面艦艇而言，早期試驗規程中對于典型目標的命中區域為長一百多米、寬十余米、高幾米的長方體，若飛行器落入該命中域即為命中目標。但是實際飛行試驗中使用的點源雷達艦船靶的雷達散射特性與真實艦船差別較大，使用理想的典型大型艦船目標的命中域去判定對點源雷達艦船靶的命中顯然是不合適的。在新的試驗規程GJB 6671-2009中專門提出了針對點源雷達艦船靶目標的命中域判據，新規程規定以飛行器末端攻擊目標的方向為基準，反射體中心為原點，左右十幾米寬，高出水面幾米的長方形為命中域，即反艦飛行器低彈道飛行對靶標為“點目標”判別準則為：以反射體中心為中心，左右±Ld，距水面高度Hd[10]。

3.2 反艦飛行器命中域判據的討論

國外某大型艦艇的側向示意圖如圖2所示。

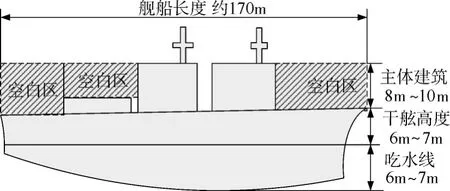
圖2 某大型艦艇側向示意圖

圖2中可以直觀看出，主體建筑以下、吃水線以上的矩形區域存在大塊的空白區域，接近總面積的三分之一左右，飛行器命中空白區域是無法造成殺傷的，因此對于飛行器的命中區域尤其是命中高度做進一步的約束是十分必要的。

目前反艦飛行器飛行試驗靶標主要使用點源雷達艦船靶、分布式雷達艦船靶和實體艦船靶三類。點源雷達艦船靶一般為非機動靶，主要用來驗證飛行器的側向命中精度，影響飛行器側向命中精度的誤差源主要取決于導引頭的測量精度和飛行器的控制精度，顯然對于反艦飛行器射擊非機動點源雷達艦船靶要求側向命中區域為左右十幾米寬是偏寬松的，無法達到飛行器實際使用情況下的命中精度要求。針對當前飛行器控制系統的技術性能，射擊非機動點源雷達艦船靶側向命中區域要求達到幾米的量級是合理的。

中小型艦艇類目標船舷較低，幾米的命中點高度難以對艦艇造成致命毀傷，容易出現從艦艇甲板上方掠過的可能，試驗中必須要對命中點高度的下限和誤差范圍進行更加嚴苛的考核。飛行器武器系統設計中是對命中點高度有明確要求的，在飛行試驗中根據試驗需求對命中點高度進行射前裝訂，所以命中高度判據應該與裝訂的命中點高度密切相關，而不應該是一個統一的范圍。影響飛行器命中點高度的誤差源主要取決于高度表的測量精度和飛行器的控制精度，這個誤差是很小的，結合以往歷次飛行試驗打靶結果，命中點高度與裝訂高度的誤差能夠達到米的量級。設飛行試驗裝訂的命中點高度為Hzd，則命中點高度判據建議設為[Hzd-ΔH，Hzd+ΔH]，ΔH可根據飛行器的控制系統性能設定。

4 利用遙測數據估算飛行器脫靶量

脫靶量是飛行器飛行試驗中的關鍵測量參數，直接反映飛行器的命中精度。獲取脫靶量的手段很多，包括張網測量檢靶法、光學測量法、無線電測量法等。但在一些特殊情況下，以上測量手段均無法獲取到飛行器脫靶量數據，這時就希望使用彈上遙測數據來分析飛行器的命中精度。

4.1 基于衛星導航信息估算脫靶量

反艦飛行器中段制導一般采用慣導/衛星組合導航方案，衛星導航信息可作為外測彈道測量信息，靶船上裝有衛星定位系統，通過飛行試驗事后數據處理，可以將飛行器、靶船和差分基準站的衛星測量信息進行差分綜合處理，獲得高精度的飛行器和靶船位置數據，進而計算出高精度的脫靶量數據。以某發飛行器飛行試驗為例，飛行器飛行軌跡與靶船位置相對關系如圖3所示，根據飛行器位置信息和靶船位置信息計算的彈目距離曲線如圖4所示[11～12]。

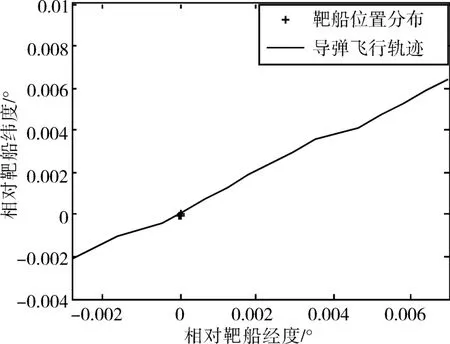
圖3 飛行器航跡與靶船位置關系示意圖

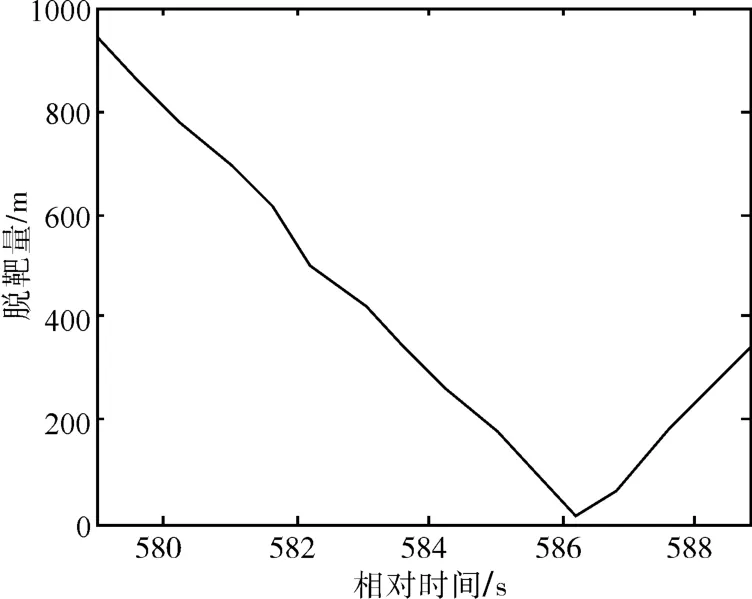
圖4 基于衛星導航信息估算脫靶量曲線

設飛行器某瞬時的經度和緯度為（Em(i)，Nm(i)），靶船某瞬時的經度和緯度為（Et(i)，Nt(i)），則飛行器過靶時刻的彈目距離為

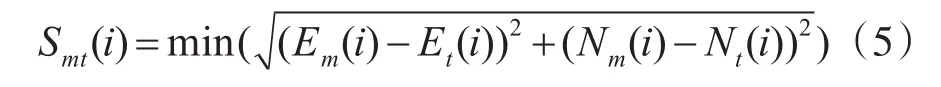
利用式（5）可以找出飛行器過靶時刻的經度和緯度，飛行器過靶前一時刻位置點A、飛行器過靶后一時刻位置點B與此時靶船位置點C構成平面三角形關系，設該平面三角形的三個邊長為AB、AC和BC，三個角度為∠A、∠B和∠C，A、B、C三點的經度和緯度可根據遙測數據獲得，進而可以求出AB、AC和BC，結合余弦定理可以求出飛行器中靶時刻的脫靶量：

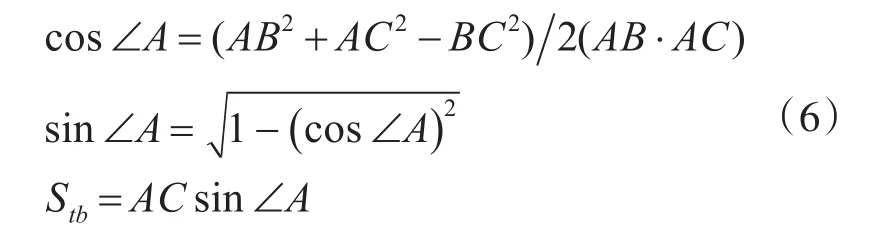
去除靶船定位系統布設位置與靶船角反射體中心位置誤差后，利用衛星導航測量數據估算脫靶量的誤差σtb主要取決于飛行器定位誤差σm和靶船定位誤差σb，關系式為

聯合3.1節中關于側向脫靶量的定義，σtb滿足以下要求：

假定側向命中區域為左右15m，通過衛星導航數據估算的側向脫靶量為5m，一般情況下σm≈σb，本次試驗衛星導航定位精度如果能達到7m，既可以滿足試驗需要。經過事后差分綜合處理衛星導航定位精度達到這個水平是可實現的，因此利用衛星導航定位信息估算飛行器脫靶量方法是有工程實用價值的。

4.2 基于導引頭測量信息估算脫靶量

上節中已經論證了利用衛星導航數據估算飛行器脫靶量方法是可行的，但是該方法的使用也受到了一定的限制。例如在飛行器末段無法提供衛星導航信息的情況下，飛行器依靠慣導系統和雷達導引頭進行導航。慣導系統的誤差較大，可能是幾十米甚至百米以上的誤差，這個誤差對于脫靶量的估算是不能接受的。

雷達導引頭對于彈目距離、目標方位的測量比較準確，同時慣導系統對于飛行器姿態角和速度的測量精度也是比較高的，尤其是在彈目距離比較小的情況下，以上誤差尚未發散，能夠滿足脫靶量估算要求。

設雷達導引頭跟蹤下限前最后一幀數據時刻為計算零點，以此時刻飛行器質心在水平面上的投影點為原點O，ON軸指向地球真北方向，OE軸指向地球正東方向，OX軸為飛行器縱軸在水平面上的投影，OV軸為飛行器運動方向在水平面上的投影，OT為飛行器質心與靶標中心的連線，飛行器與靶標位置關系如圖5所示[13]。

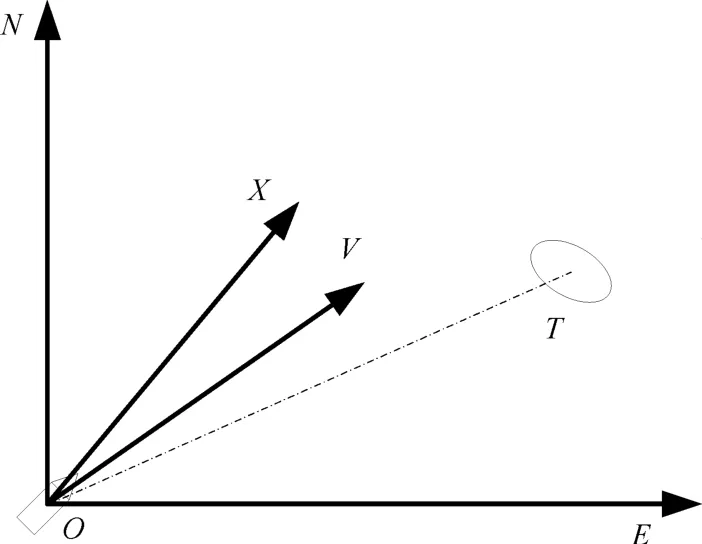
圖5 飛行器與靶標位置關系示意圖

∠XON為飛行器的航向角，∠VON為飛行器的航跡角，∠VOX為飛行器的偏航角，∠TOX為雷達方位角。通過組合導航系統和雷達導引頭遙測數據能夠獲取到每一幀航向角、航跡角和雷達方位角的彈上測量值，結合雷達導引頭測得的彈目距離SMT，可以得到靶船在O-EN坐標系下的位置方程為

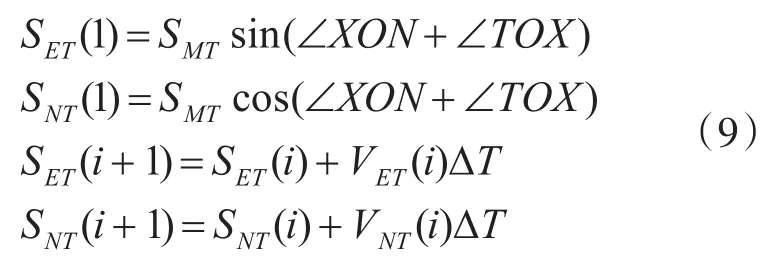
SET(i)、SNT(i)為靶船的東向位置和北向位置，VET(i)、VNT(i)為靶船的東向速度和北向速度，ΔT為遙測數據幀時間間隔。如果靶船為非機動靶，則VET、VNT默認為0。

飛行器在O-EN坐標系下的位置方程為

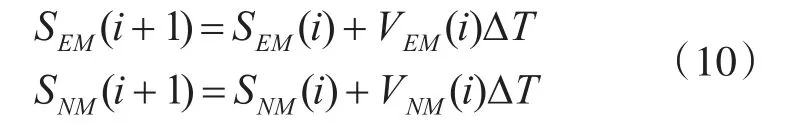
SEM(i)、SNM(i)為飛行器的東向位置和北向位置，初始位置為0、0，VEM(i)、VNM(i)為飛行器的東向速度和北向速度。

則彈目距離SMT變化趨勢為

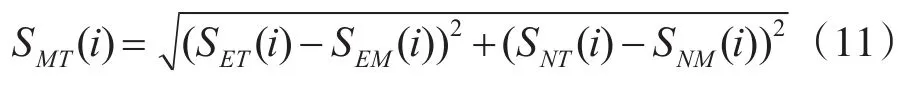
從計算零點開始，逐幀計算彈目距離SMT，當其取到最小值min[SMT(i)]時，則認為此刻為彈目交匯點，min[SMT(i)]為脫靶量。

通過導引頭測量數據估算脫靶量誤差主要取決于彈上角度、速度和彈目距離的測量精度，一般來說，角度測量精度能達到角分量級，速度測量精度能達到m/s量級，彈目距離測量精度能達到米的量級，從計算零點開始到彈目交匯時刻的時長小于1s，經理論分析該脫靶量估算方法的誤差能夠達到米的量級。利用實際飛行試驗數據進行對該方法進行驗證，如表3所示。

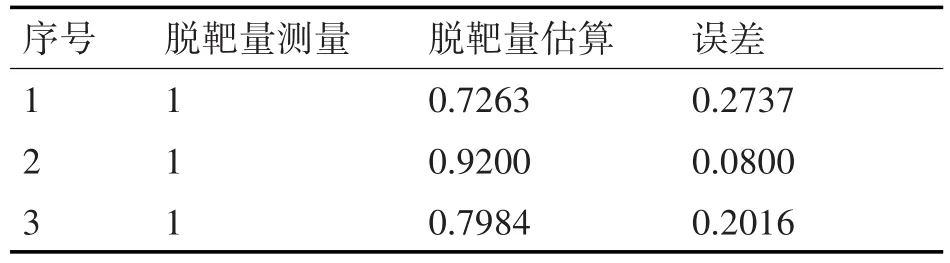
表3 基于導引頭信息估算脫靶量精度

通過以上分析可以看出利用雷達導引頭遙測數據進行脫靶量估算是比較準確的，但是利用飛行器自身測量數據判定飛行器命中精度不應作為脫靶量判定的主用手段，在該方法的使用中應當注意以下幾點：

1）針對靶場試驗而言，應該在每次飛行試驗后使用多種方法對脫靶量進行比對分析，確定各種脫靶量測量手段的可行性及測量精度；

2）實際飛行試驗中脫靶量測量應以靶載設備測量結果為準，在靶載設備無法有效獲取脫靶量數據的情況下，可以利用雷達導引頭遙測數據進行脫靶量估算輔助開展命中精度分析；

3）該方法對靶船雷達散射點比較集中的點靶計算精度較高，對于雷達散射點散布較大的復合靶或實體艦船要針對雷達導引頭的跟蹤情況進行細致的分析。

5 結語

命中精度指標是飛行器武器系統最重要的戰術技術指標之一，與武器毀傷能力息息相關。反艦飛行器武器試驗一直使用單發命中概率來描述命中精度指標，現在看來單發命中概率并不能夠代替命中精度指標，本文討論了靶場一直使用的“N發M中”的單發命中概率試驗方案存在著理論基礎缺陷，在靶場飛行試驗中難以構建出理想的實際檢驗條件，而新形勢下的試驗鑒定工作要求在性能試驗多安排抗干擾飛行試驗，以上種種情況都要求我們不能再拘泥于傳統的單發命中概率檢驗方法來考核命中精度。而是應該綜合運用理論分析、仿真計算和飛行驗證多種手段，對每一次飛行試驗中激勵出來的影響命中精度的誤差源進行更加系統的分析，將其迭代入理論模型和仿真模型對命中精度開展綜合分析，最終對反艦飛行器命中精度指標給出更加科學準確的評定結論。