船舶軌跡快速相似度度量與改進自適應密度聚類

李 湘 劉 奕

(武漢理工大學航運學院1) 武漢 430063) (內河航運技術湖北省重點實驗室2) 武漢 430063)(國家水運安全工程技術研究中心3) 武漢 430063)

0 引 言

船舶軌跡由一系列二維經緯度點構成，因此船舶相似度度量方法能夠測量不同軌跡間的距離[1-3]．在歐式距離測量算法中，要求船舶軌跡點的長度必須對齊，即每艘船的軌跡點數量必須相同，而在實際中因每艘船的航速不同導致AIS基站獲取每艘船舶的AIS報文數量也各不相同，因此該算法無法很好的應用在船舶軌跡相似性度量中．Hausdorff距離、隱馬爾科夫模型無需要求船舶軌跡點數量必須相同，但二者卻不能很好的對船舶軌跡進行相似度度量，存在較大的測量誤差．最長公共子序列(LCSS)算法適用于測量形狀相似度，且計算時間開銷較大．動態時間規整(DTW)算法能夠計算出船舶軌跡間的形狀相似度與距離相似度，且該算法被廣大學者用于度量船舶軌跡間相似度，進行語音信號分類識別、時間序列信號分析和手寫信號識別分類分析．Liu等[4]運用DTW度量船舶軌跡間的相似度距離并根據該距離對船舶軌跡進行聚類以此挖掘船舶習慣航路．Li等[5]運用DTW度量船舶軌跡間距離并提出多步聚類算法用于船舶異常軌跡識別．Zhao等[6]將船舶軌跡形狀結合DTW算法用于分析船舶軌跡間距離并挖掘船舶習慣航路．DTW算法雖被廣大學者應用于船舶軌跡間相似度度量，但該算法由于其復雜度為O(n2)，且在應用于海量船舶AIS數據中存在計算時間開銷過大的問題．基于此，文中相似度度量算法能夠對船舶軌跡進行快速特征提取，并快速測量船舶軌跡間相似度，提升了相似度度量算法的速度性能，且不影響最終聚類性能．

在將海量AIS數據結合聚類算法分析船舶運動特征、船舶整體運動規律并為挖掘船舶習慣航路、探索發現、分析船舶異常行為的過程中，密度聚類算法(DBSCAN)被廣泛應用．Zhen等[7]利用AIS數據結合密度聚類算法挖掘船舶會遇場景．Pallottad等[8]提出一種基于密度聚類的偏差變化算法結合船舶轉向點用以挖掘船舶交通流習慣航路．Yan等[9]提出一種基于密度聚類的非監督學習算法用以識別船舶停止與航行點特征．Liu等[10]對密度聚類算法進行改進并考慮船舶軌跡點速度與方向特征用以提取船舶正常航行軌跡．

由于密度聚類算法其自身存在參數半徑r與最少點數minpts難以確定，且該算法人為操作量較大．文獻[11]雖提出了自適應密度聚類算法，但在確定參數r與minpts過程中的擬合分布算法導致密度聚類存在普適性問題，導致該算法無法適用于其他水域．因此本文為對這一缺陷采用核密度估計算法改進自適應密度聚類，完全依據原始數據自身特性，從數據自身實際出發對數據分布進行擬合進而確定密度聚類算法中的r與minpts參數，提升了算法的智能性與適用性，且不影響最終的密度聚類性能，并以長江南槽交匯水域AIS數據作為算法驗證集，分別驗證了快速相似度度量與改進自適應密度聚類算法．

1 快速相似度度量方法

船舶軌跡間的相似度是對船舶軌跡群聚類分析的重要因素，目前存在很多測量軌跡間相似度的方法，動態時間規整(dynamic time warping，DTW)在測量船舶軌跡間相似性領域中應用較多且性能較其他算法突出，DTW計算公式為

DTW(1,1)=d(1,1)

DTW(i,j)=d(i,j)+min[DTW(i,j-1),

DTW(i-1,j-1),DTW(i-1,j)]

(1)

式中：i,j分別為相似度距離矩陣中的行列值．

但DTW仍需要遍歷計算所有對應點之間的距離，其復雜度為O(N2)，在涉及計算大量船舶軌跡間相似度時，該方法存在復雜度過高，計算時間過長的缺陷，不利于快速提取船舶軌跡間相似程度．針對DTW復雜度過高的問題，本文提出了一種基于船舶軌跡經緯度均值特征的新型快速相似度度量方法．快速相似度度量算法流程見圖1．

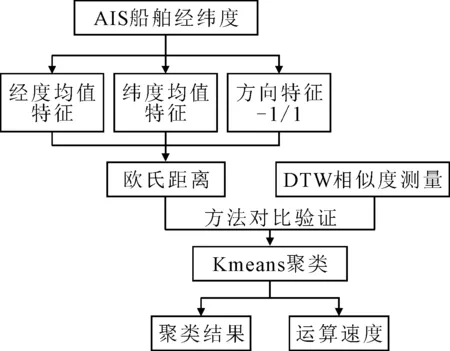
圖1 快速相似度度量算法

方法建模過程如下.

步驟1提取AIS數據中各船舶軌跡經緯度信息，為

route1=[[X1,y1],[X2,y2],…]

…

(2)

式中：X為經度；y為緯度．

對各船舶軌跡經緯度進行均值處理，將多點二維信息轉換為單點二維信息，為

route1=[Xmean,ymean]

…

步驟2設定方向判別閾值 本實驗水域為長江南槽交匯水域，水域經度范圍為東經121.68°至東經121.75°，水域緯度范圍為北緯31.27°至北緯31.35°，水域航道見圖2．

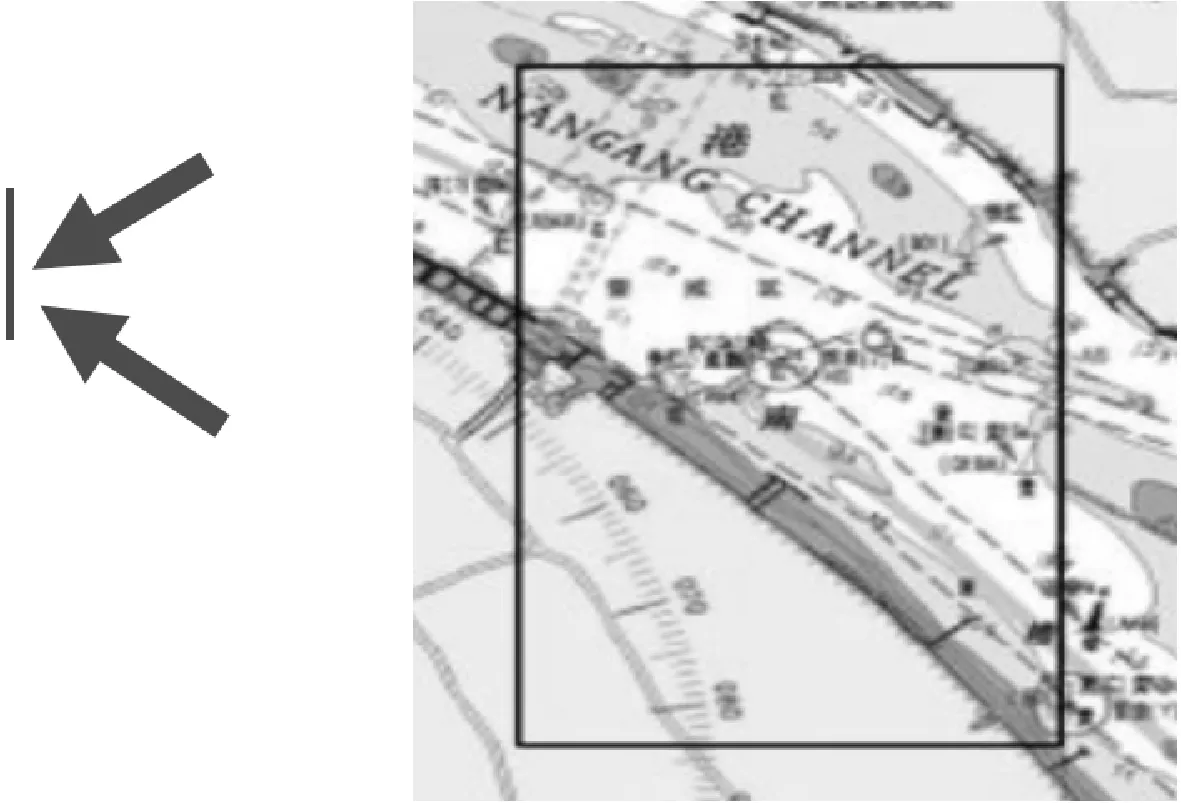
圖2 航道水域

圖2中箭頭所指向的豎線為方向判別閾值，該豎線對應經度121.70°，將其設定為方向判別閾值，若軌跡起點經度大于121.70°，則判定該船舶自右向左航行，對該船舶軌跡提取的二維特征信息增加-1值作為方向判別特征，即

routeright=[Xmean,ymean,-1];

若軌跡起點經度小于121.70°，則該船舶自左向右航行，則對該船舶軌跡提取的二維信息增加1值作為方向判別特征，即

routeleft=[Xmean,ymean,1];

對所有軌跡均按照上述方式增加方向特征信息．船舶間的相似度度量轉換為兩兩軌跡間三維信息特征的歐式距離，即兩船舶軌跡間相似度度量值的平方

(方向值′-方向值″)2

步驟3方法驗證 提取該水域中120條船舶軌跡的AIS信息，總計39 241對經緯坐標，且該水域航道為兩路交叉水域航道，且同一航道內存在東西雙向航行船舶即雙向航路，因此，交叉水域內按照航道的不同將船舶軌跡分類兩類，同一航道內又存在雙向航路，所以最終將軌跡聚類簇數設定為四類，同時為驗證快速相似度度量方法的適用性，本實驗將快速相似度度量方法結合k-means聚類(k=4)與DTW結合k-means(k=4)進行聚類效果對比與運算速度分析, 聚類效果對比見圖3～4．

圖4 k-means結合DTW

由圖3～4可知：在驗證快速相似度度量方法的適用性時，快速相似度度量方法結合k-means與DTW結合k-means的最終聚類效果相同，均能夠將交叉水域不同道航與各自航道內不同方向的船舶軌跡群區分開來，得到最終的四類簇．

在驗證快速相似度度量運算速度的過程中，本實驗分別對兩種測量方法運行6次，觀測運算時間，見表1．

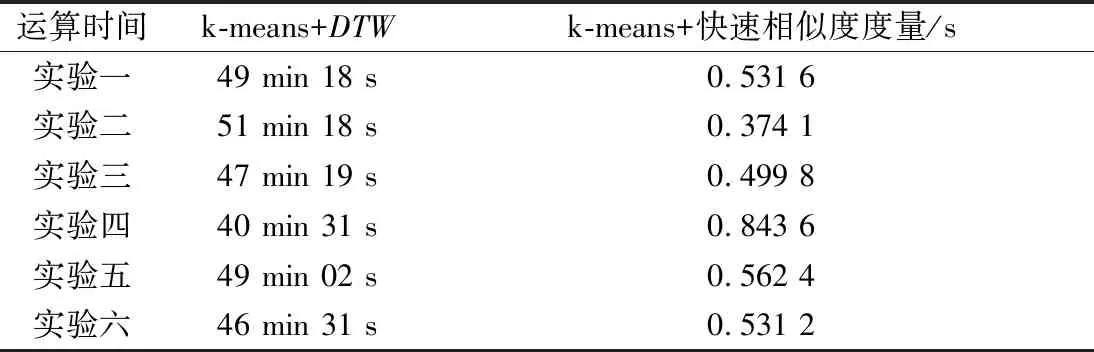
表1 運算時間表

由表1可知：快速相似度度量算法相比較傳統DTW算法，聚類速度提升近5 061倍．在計算處理大數據船舶軌跡時，該方法可大幅縮短聚類計算時間且不影響聚類性能．

2 改進自適應密度聚類

密度聚類可用于對船舶軌跡分析、挖掘船舶習慣航路，該算法可快速識別具有相似特征的船舶軌跡簇，且能夠剔除噪聲、船舶離群軌跡點等．但該算法存在參數r與minpts難以確定的問題，需要多次人工實驗以獲得最優參數．本文提出改進自適應密度聚類算法以提升算法性能，流程圖見圖5．

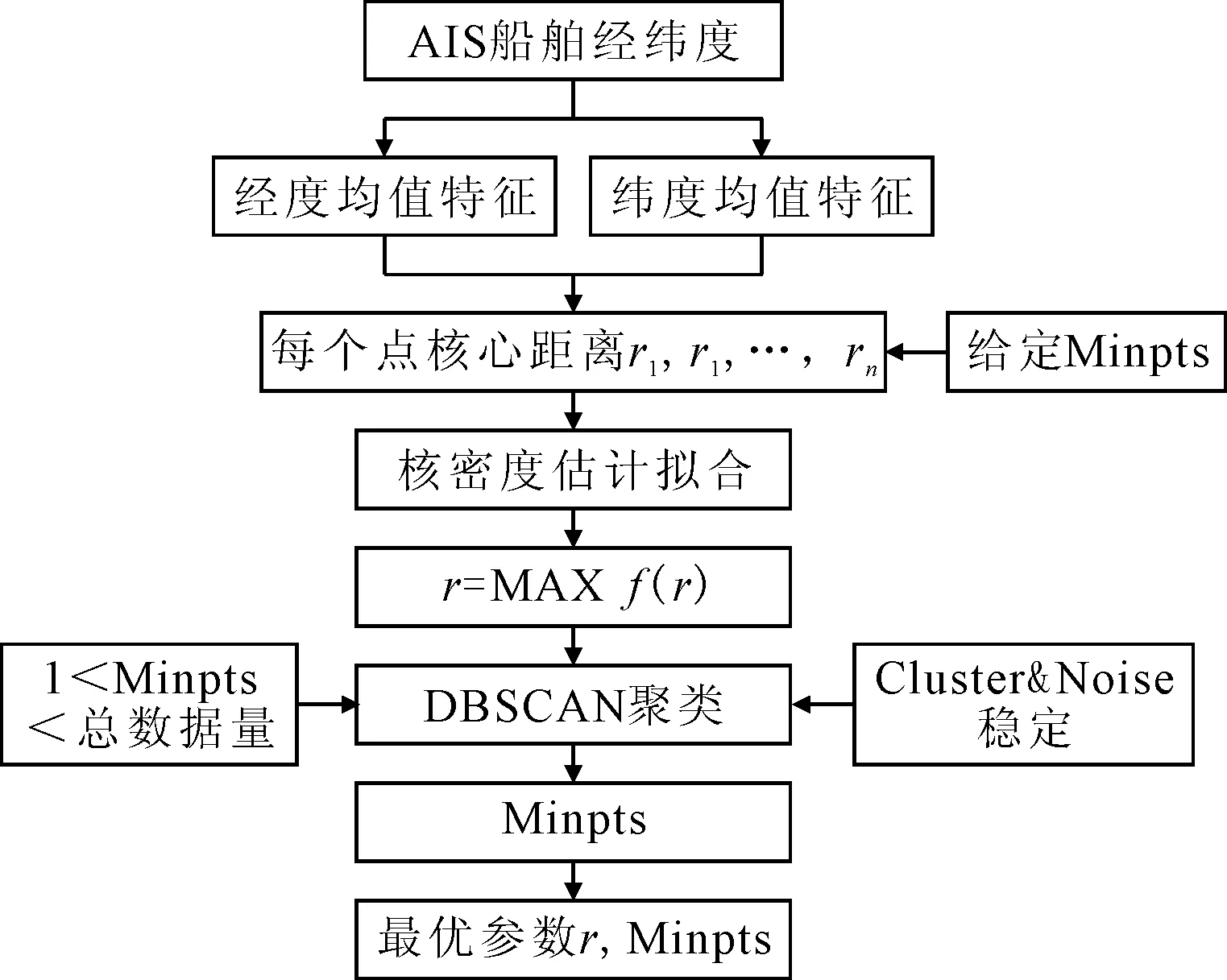
圖5 改進自適應密度聚類流程圖

DBSCAN算法原理：基于密度的空間聚類算法能根據樣本分布的緊密程度將數據分為幾類簇，以數據集在空間分布的稠密程度為標準進行聚類處理，若某一區域中樣本的密度值大于設定的某個閾值，則將該樣本劃入與之相近的類簇中．密度聚類能夠識別所有密度相連的樣本集，并將這些樣本集聚成多個類簇，其主要特點為：能夠發現任意不規則形狀的簇、對噪聲數據不敏感．

1) 參數選取 DBSCAN算法中有兩個重要的參數鄰域半徑r和最少數據量minpts需要人為確定，在設定這兩個參數的過程中，不同的參數組合將對最終聚類效果產生很大影響，特別是在對大量船舶軌跡數據進行聚類時，參數的確定較為困難，且參數選取范圍較廣泛，只能由操作人員逐個嘗試選取最優結果．

根據參考文獻[11]中參數確定的方法包括：運用統計學方法計算兩個參數之間最優的參數選擇．具體確定方法如下：在確定鄰域半徑r的過程中，鄰域半徑r能夠保證該元素成為核心點，在理想化的密度聚類過程中，數據較為集中的高密度區域內數據都能夠各自成為核心點，并且各數據能夠匯聚成簇使得該類簇的密度最大．針對一個單獨的數據而言，在給定minpts時，最小半徑r能使得該數據成為核心數據點并且保證類簇成形，因此在給定minpts條件下最優的半徑r能使得最多的數據點成為核心數據點并且類簇成形．

根據這一原理，首先采取文獻[11]對半徑數據集樣本點采取逆高斯概率密度函數(3)擬合后求取半徑數據集核心距離的眾數(6)以確定最終半徑參數r:

(3)

(4)

(5)

(6)

式中：逆高斯分布中的λ和μ均分別由最大似然估計法(4)和(5)獲得，經過計算得出r=0.002 26．

在最小元素數量minpts參數確定過程中，minpts的取值范圍是從1開始增加到樣本總數的整數值，當minpts為1時，單個數據也可成為一簇，隨著minpts數量的持續增加，聚類過程中的可以看做是每個子類簇持續合并周圍數據的過程，但隨著minpts數量逐漸增加，許多較近的類簇之間被互相吸納合并為一類，因此在聚類在達到穩定理想態之前，類簇之間合并速度較快，類簇和噪聲的數量均大幅減少，隨著聚類狀態趨向理想穩態化，各簇之間的距離相對較遠，類簇和噪聲的數量趨于穩定，在達到理想狀態時，最終類簇和噪聲數量維持恒定．由圖6觀測到類簇和噪聲數量趨于平穩處的minpts為13．

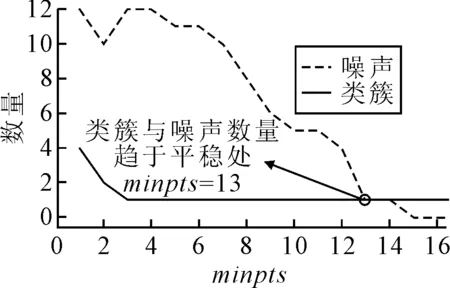
圖6 類簇和噪聲數量

因此，將0.002 26和13作為密度聚類的r和minpts參數，聚類結果見圖7．

圖7 DBSCAN結合逆高斯分布

實驗結果圖7表明采用文獻中[11]所提供的自適應密度聚類算法無法將交叉水域不同道航與各航道內不同方向的船舶軌跡群區分開來，僅得到兩類聚類簇．經分析得出結論該算法強制采用逆高斯分布擬合密度聚類過程中的半徑分布而沒有從實際數據出發對半徑分布進行擬合．

因此針對文獻[11]中方法存在聚類性能不足的問題，文中考慮更換擬合函數算法．經查閱資料，核密度估計算法存在普適性優點，包括擬合過程完全從數據自身特性出發，利用數據自身的實際值去估計總體樣本的概率密度函數，依據樣本點對應的概率密度函數值越大越接近峰值，則該樣本點附近的數據越集中且該樣本極具代表性的這一原理，文中采取核密度估計擬合核心距離半徑r的概率密度函數．核密度估計公式：

(7)

式中：n為數據個數；k為本文采用的高斯核函數；Xi為不同的半徑r；h為本文采取的平均積分最小誤差帶寬,

(8)

其中：σ為數據r樣本方差；n為數據個數．

根據概率密度函數的實際意義可知，在概率密度函數峰值處左右的數據較為集中，原始數據集中數據點越稠密的區間內概率密度函數值越大．依據這一原理，在給定minpts下，文中從多個實際核心距離r為出發點，利用核密度估計求取核心距離r的概率密度函數，將核心距離r帶入到概率密度函數中，概率密度函數值越大其對應的核心距離r代表數據越集中且類簇成形，所求得最大概率密度函數值對應的r即為最優核心距離．核密度擬合見圖8．

圖8 核密度估計擬合

因此在給定minpts時，最小成簇半徑

r=max(f(x),x∈[r1,r2,…,rn])．

繪制在類簇和噪聲數量即將接近穩定態時參數minpts圖，見圖9．

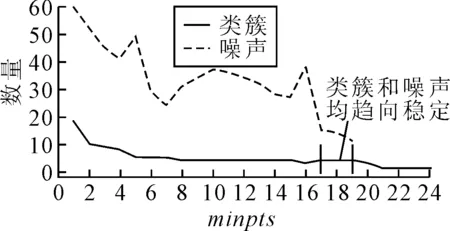
圖9 類簇和噪聲數量

由圖9可知：在確定參數minpts的過程中，圖中minpts在17至18位置附近處類簇和噪聲數量共同趨向穩定，實驗采取minpts=17時作為密度聚類中的最少元素數量，應用核密度估計minpts=17時對應的半徑r為0.003 3，在密度聚類過程中對軌跡間進行相似度度量時仍采用本文中快速相似度度量方法計算船舶軌跡間的相似度，其聚類結果見圖10．

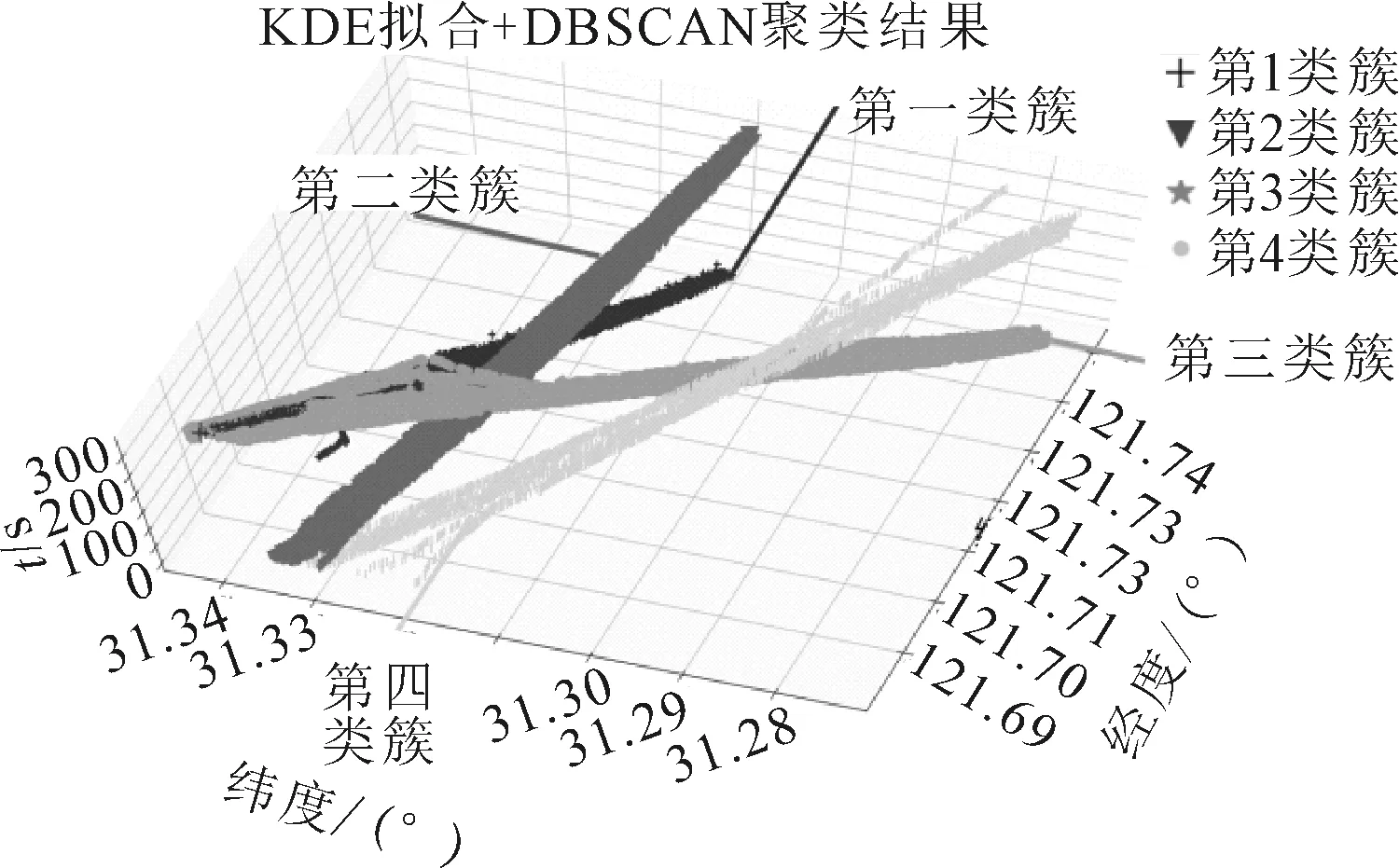
圖10 DBSCAN結合KDE

由圖7與圖10對比可以觀測到結合核密度估的DBSCAN聚類結果比結合文獻[11]中逆高斯得到的聚類結果好，結合核密度估計的自適應密度聚類算法可將不同航道以及航道內不同航向的船舶軌跡明顯區分開來，而結合逆高斯分布密度聚類算法無法區分不同航道內的船舶軌跡．若無法區分不同航道內的船舶軌跡將對探索各航道內船舶習慣航路以及研究船舶安全航行造成重大影響．

3 結 論

1) 文中提出的一種基于經緯度均值和方向閾值組合的快速相似度度量方法，在不影響聚類性能的前提下對船舶軌跡間進行相似度度量，縮短測量時間，減小內存開支，能夠針對數量龐大、運算復雜的AIS數據進行快速計算．

2) 針對DBSCAN密度聚類中的參數minpts與r需要多次人為嘗試設定的問題，利用統計學與核密度估計來確定最優參數minpts與r，該方法快速高效．

3) 通過應用本文相似度度量方法能夠對交匯水域交通流中船舶軌跡進行快速相似度度量，對U形水域以及其他異形水域的快速相似度度量方法還需進一步研究；在密度聚類過程中針對交通流過于集中的水域，如何進行更加精準的提取軌跡類簇、交通流特征與船舶異常軌跡識別是下一步的重點研究方向．