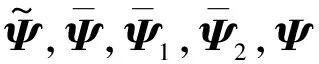考慮彈性地基的正交雙曲蜂窩夾層殼體自由振動分析

倪 臻，李旦望，夏 燁，周 凱，華宏星

(1.中國航發商用航空發動機有限責任公司，上海 200241；2.上海交通大學 振動沖擊噪聲研究所，上海 200240；3.上海交通大學 機械系統與振動國家重點實驗室，上海 200240；4.上海交通大學 高新船舶與深海開發裝備協同創新中心，上海 200240)

蜂窩夾層殼由上下面板和蜂窩芯層組成，具有質量輕、強度高的特點，并有良好的隔音、減振特性，近年來越來越廣泛地被運用于航空航天、車輛、船舶等領域。然而，蜂窩夾層殼體往往會受到復雜的環境激勵，進而產生振動，并最終疲勞破壞。因此，有必要建立可靠的動力學模型以研究蜂窩夾層殼體在外激勵下的振動響應。

楊穩等[1]指出，由于蜂窩夾層材料具有離散非均勻的特性，直接對其進行建模分析需要消耗巨大的時間和計算成本。為此，大量學者對蜂窩芯層的等效方法進行了研究，將其作為各向異性材料進行建模[2-6]。基于蜂窩芯層等效方法，Eipakchi等[7]利用經典板殼理論建立了具有負泊松比的圓柱殼模型，并計算了其在壓力載荷下的動力學響應。Duc等[8]基于一階剪切變形理論，獲得了具有負泊松比蜂窩結構的圓柱殼體動力學響應特性。王盛春等[9]基于Reissner-Mindlin理論，得到了考慮剪切變形的四邊簡支矩形蜂窩夾層板彎曲振動固有頻率的精確解。Zhang等[10]利用一階剪切變形理論，研究了懸臂三明治蜂窩夾層板的自由振動及非線性響應特性。Li等[11]基于三階剪切變形理論計算了蜂窩夾層板的彎曲振動特性。Yu等[12]采用經典板理論、一階剪切變形理論和三階剪切變形理論建立了蜂窩夾層板的動力學模型，并對采用3種不同模型得到的固有頻率進行了比較。他們指出，經典板理論與一階剪切變形理論在計算蜂窩夾層板的振動特性時具有較大的計算誤差。Liu等[13]對此現象進行了分析，認為采用低階剪切變形理論會高估夾層殼體上下面板的剪切應力，并提出了針對一階剪切變形理論的改進辦法。Sun等[14]利用有限元法計算三明治蜂窩夾層板在沖擊載荷下的響應，并通過試驗驗證了計算結果。王威遠等[15]對錐形復合材料蜂窩殼的振動傳遞特性進行了試驗研究。

值得一提的是，盡管關于蜂窩夾層板殼的研究較多，但大多集中在蜂窩夾層平板或圓柱殼、圓錐殼等簡單形狀殼體的動力學建模和分析上，且并未考慮彈性支承約束。因此，亟需對具有彈性支撐約束的復雜形狀蜂窩夾層殼體的動力學特性開展研究。為能考慮中厚蜂窩殼體的振動響應特性，本文將基于一階剪切變形理論和修正的Gibson公式建立考慮彈性地基的雙曲蜂窩夾層殼體控制方程，并對其自由振動特性進行分析。

1 理論模型

1.1 運動學及動力學關系

雙曲蜂窩夾層殼體的結構示意圖，如圖1所示。圖1中：hc為峰窩芯層厚度；h為殼體總厚度。蜂窩夾層殼體是由上下面板及蜂窩芯層組成的空間三維結構。殼上任意一點的空間坐標可由其中面幾何形狀及對應的厚度表示。對正交雙曲殼體，其中面可用參數方程r=r(ξ1,ξ2)表示，其中:r為殼體中面的參數方程；ξ1和ξ2為曲面的正交廣義坐標，其取值范圍為ξ10≤ξ1≤ξ1L，ξ20≤ξ2≤ξ2L。在給定了殼體中面幾何后，殼體上任意一點的空間位置即可由正交參數坐標(ξ1,ξ2,ζ3)進行表示。其中，ζ3為殼上一點到殼體中面的有向距離，其正向為r(ξ1,ξ2)定義的殼體曲面法線方向。

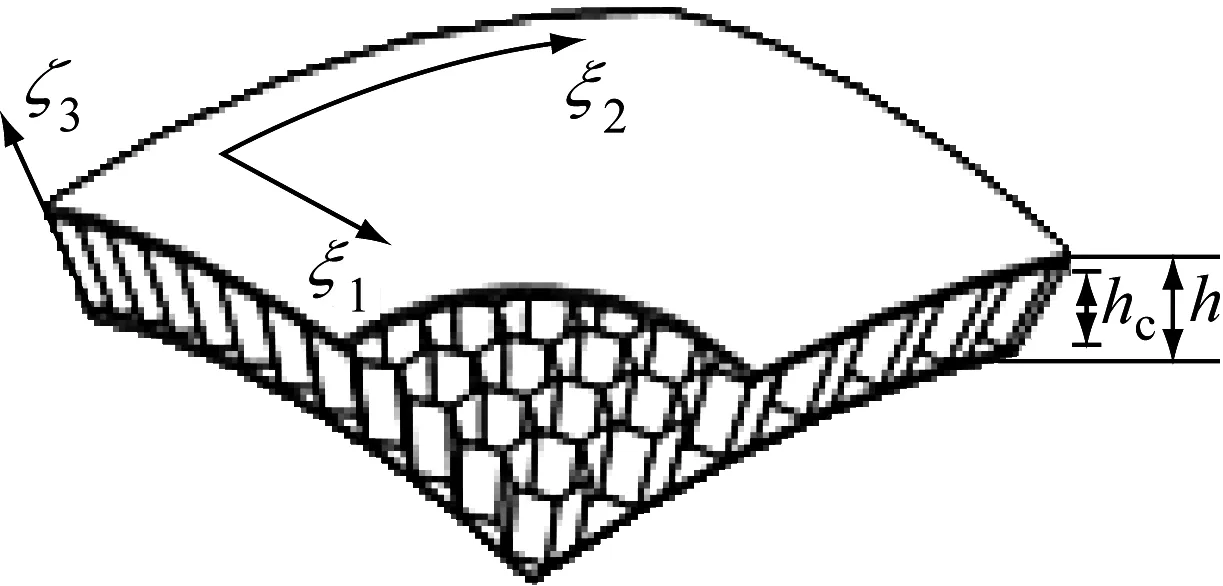
圖1 雙曲蜂窩夾層殼體

為了考慮殼體剪切變形和轉動慣量對系統動力學特性的影響，可以采用一階剪切變形理論給出殼體在曲面坐標下的位移場表達式

(1)

式中:u1,u2,u3分別為殼體上任意一點沿ξ1，ξ2，ζ3方向的位移；t為時間；u0，v0和w0為殼體中面上一點的位移；φ1和φ2為剪切轉角。

殼體的線性應變位移關系可以通過三維小變形理論得到[16]

(2)

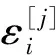
蜂窩芯層及面板的應力應變關系由文獻[17]給出

(3)

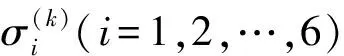
(4)

其中

(5)

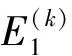
(6)

蜂窩芯層一般為由各向同性材料制備而成的六邊形周期結構，其中的單個胞元如圖2所示。圖2中:蜂窩胞元的壁厚為tc；壁長分別為l1c和l2c;蜂窩胞元壁的斜邊角度為θc。此類蜂窩結構可等效為正交各向異性材料，其等效參數由改進的Gibson公式給出

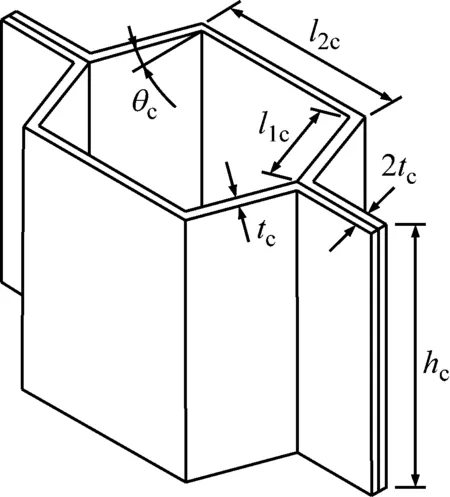
圖2 蜂窩胞元

(7)

式中：Ec,Gc和ρc分別為蜂窩芯層所用材料的彈性模量、剪切模量和密度；ρ(2)為蜂窩芯層等效密度；η1=l2c/l1c，η2=tc/l1c。

1.2 蜂窩夾層殼體能量方程

蜂窩夾層殼體的動能表達式為

(8)

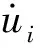
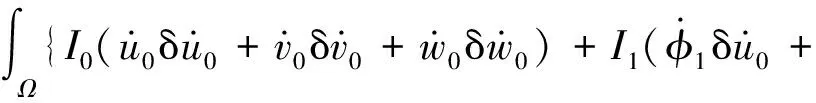
a1a2dξ1dξ2

(9)

式中：δ為變分符號；a1和a2分別為ξ1和ξ2方向的拉梅系數；Ii為考慮了曲率之后的第i階慣性矩(i=1,2,3)

(10)

殼體的應變能表達式為

(11)

式中，σij和εij分別為殼體應力場和應變場。將式(2)和式(3)代入式(11)并取變分，可以得到

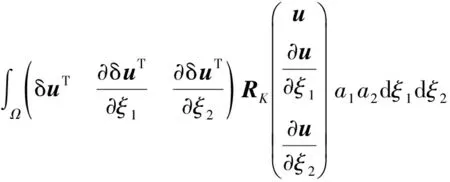
(12)

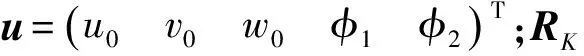
考慮殼體邊界及彈性地基所做虛功，其表達式為沿邊界方向的線積分

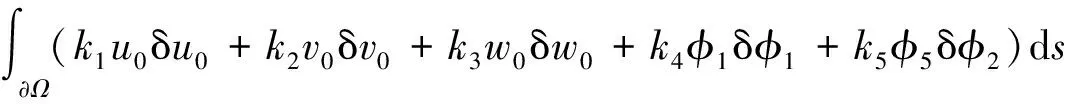
(13)

式中：k1，k2和k3為沿u，v和w方向的平動剛度；k4和k5為沿φ1和φ2方向的轉動剛度。彈性地基所做虛功[18]為

(14)

式中，ke為彈性地基剛度。

系統的總虛功為邊界條件和彈性地基所做的虛功的疊加，即有

δV=δVBC+δVe

(15)

1.3 基于改進傅里葉法的殼體振動求解

對任意邊界條件下的殼體，可以采用改進傅里葉法[19]進行求解。將殼體位移場利用傅里葉級數進行展開

(16)

式中：Umn(t)，Vmn(t)，Wmn(t)，Φ1mn(t)和Φ2mn(t)均為殼體位移的廣義坐標；U0(t),V0(t)，W0(t),Φ1(t)和Φ2(t)分別為其對應的向量形式；φm(ξ1)和ψn(ξ2)分別為對應ξ1和ξ2的傅里葉基函數;Ψ(ξ1,ξ2)為傅里葉基函數對應的向量形式；M和N分別為對應基函數的階次。φn和ψn的表達式分別為

(17)

(18)

將式(16)代入哈密頓原理表達式

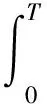
(19)

即可得到如下矩陣方程

(20)

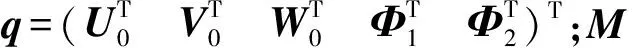
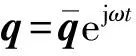
(21)

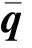
2 數值分析及討論

2.1 收斂性分析及方法驗證

為了驗證給出方法的可靠性，首先建立一含蜂窩芯層的殼體模型。殼體的曲面參數方程為

r=[ξ1,f(ξ1)sinξ2,f(ξ1)cosξ2]

(22)

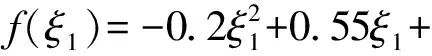
首先對模型的收斂性進行驗證。分別采用本文給出的方法和商用有限元軟件ABAQUS建立蜂窩夾層殼體模型。在采用有限元法進行建模時，采用的單元類型為二階減縮積分四邊形殼體單元S8R，建立的網格總數為2 120，如圖3所示。當選取不同階次基函數時，四邊簡支的蜂窩殼固有頻率及其與有限元結果的比較，如表1所示。從表1可知，采用本文給出的方法計算得到的系統固有頻率與有限元法計算得到的結果吻合良好。采用兩種方法計算得到的系統振型，如表2所示。從表2可知，本文給出的方法亦能夠準確計算蜂窩殼的振型。表1還給出了采用不同方法所消耗的計算時間。從結果可知，由于推導得到了殼體的半解析解，此方法具有很高的計算效率。

圖3 殼體有限元模型

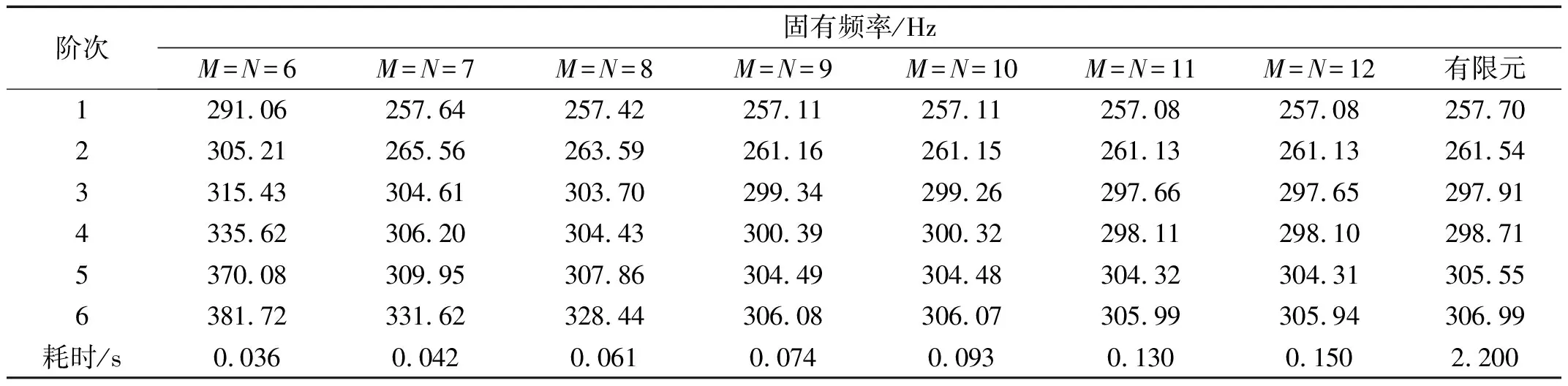
表1 不同階次基函數系統的固有頻率

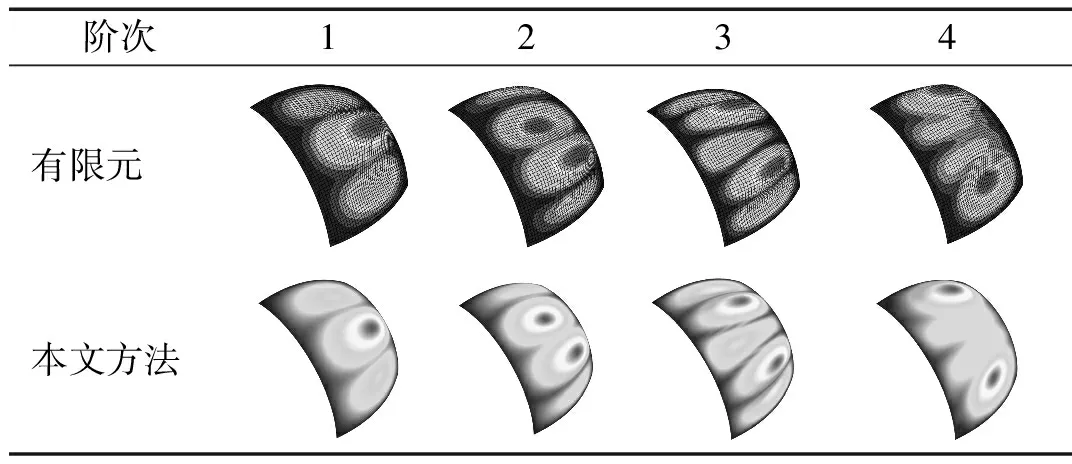
表2 殼體振型對比

接下來考慮彈性地基對系統固有頻率的影響。殼體在不同地基剛度下的前4階固有頻率，如圖4所示。從圖4可知，當地基剛度值小于1×106Pa/m時，系統的固有頻率隨地基彈性的變化并不明顯。而當地基剛度值大于1×109Pa/m時，其固有頻率也趨于定值。當地基剛度值在106～109Pa/m時，系統的固有頻率隨地基彈性地增大而迅速增大。這是由于彈性地基的引入約束了殼體沿中面法向的運動，從而提高了系統的剛性，因此在考慮了彈性地基后，殼體的固有頻率有了顯著地提高。當地基彈性達到1×109Pa/m時，地基可以認為是剛性的，因此此時繼續增大地基剛度不會影響系統的固有頻率。而當地基彈性小于1×106Pa/m時，由于其剛度值較小，地基并不會對系統的動力學特性產生顯著影響。因此，此時系統的固有頻率隨地基彈性的變化并不明顯。

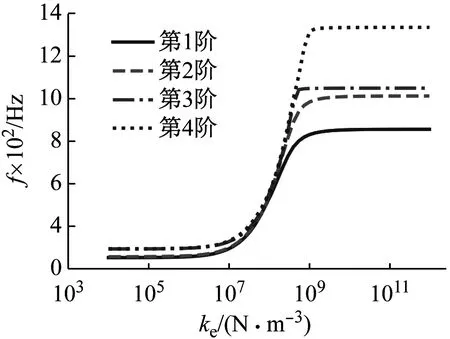
圖4 固有頻率隨彈性地基剛度的變化

2.2 參數分析

2.2.1 芯層厚度比

改變蜂窩夾層殼的結構參數，討論芯層厚度比對系統固有頻率的影響。保持殼體的總厚度h=20 mm為定值，改變蜂窩夾層殼的厚度比η=hc/h。當地基剛度分別為0，2×108Pa/m和2×109Pa/m時，系統的前4階固有頻率隨厚度比的變化關系，如圖5所示。從圖5可知:當ke=0時，系統的固有頻率隨η地增大而減小;且隨著η的增大，系統固有頻率的下降速度也逐漸增大;當ke=2×108Pa/m時，系統的固有頻率首先隨厚度比的增大而升高;但隨著厚度比繼續增大，系統固有頻率開始迅速下降;類似的，當ke=2×109Pa/m時，系統的固有頻率隨厚度比地增大而先增大后減小。

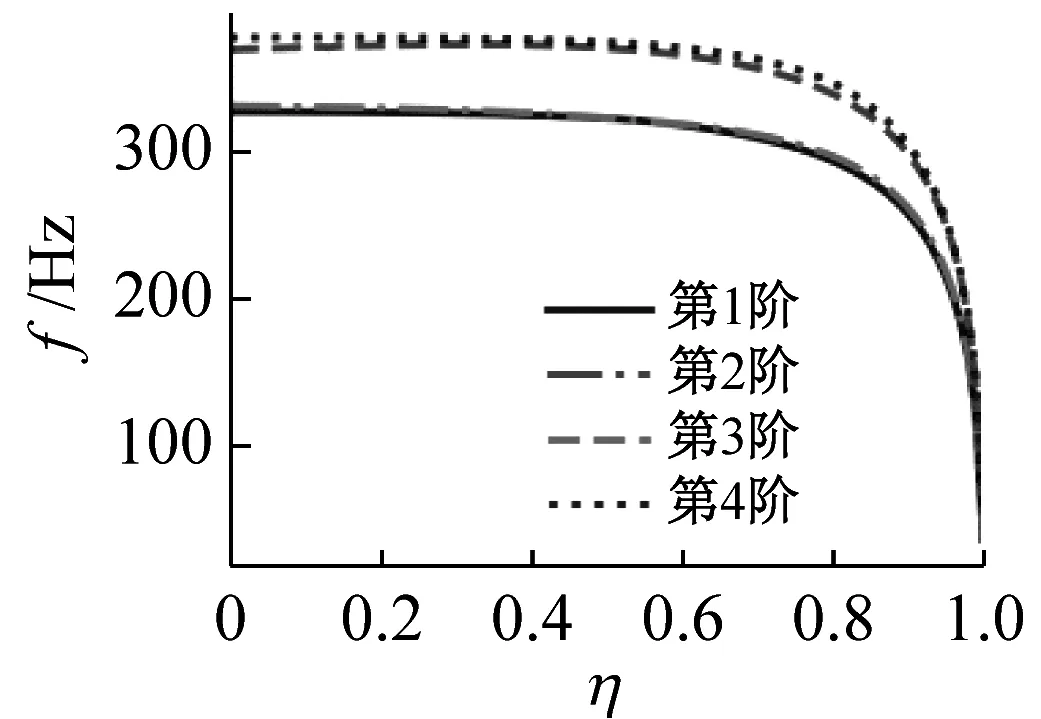
(a)ke=0

事實上，系統的固有頻率取決于模態坐標下系統各階剛度與質量的比值。系統的模態質量越大，則對應模態的固有頻率越低；系統的模態剛度越大，則對應模態的固有頻率越高。在本算例中，增大蜂窩厚度比會同時減小系統的剛度和質量。因此，系統固有頻率的變化情況取決于模態質量與模態剛度隨蜂窩厚度比的相對變化情況。對于蜂窩夾層殼體，由于其芯層較軟，因此其剛度主要由上下面板提供。當芯層厚度比較小時，系統固有頻率隨厚度比的變化方向取決于地基剛度的大小。然而，隨著芯層厚度比地增大，其上下面板的厚度逐漸減小，面板對系統總體剛度的貢獻急劇下降，使得殼體總體剛度迅速減小。此時，無論地基剛度取為何值，系統固有頻率均會迅速降低。

2.2.2 蜂窩胞壁參數

六邊形蜂窩結構具有兩個重要的無量綱參數η1，η2，分別為六邊形蜂窩結構的邊長比和蜂窩壁厚比。為了分析其對系統動力學特性的影響，系統的前4階固有頻率隨η1和η2的變化關系，如圖6所示。在進行計算時，彈性地基剛度取為ke=2×108Pa/m。從圖6可知，改變η1對系統固有頻率的影響并不顯著。當η2較小時，增大η1會使得系統的固有頻率略有上升；而當η2較大時，增大η1則可能會降低系統的固有頻率。但是，系統的固有頻率會隨η2地增大而顯著降低。這表明，增大蜂窩壁厚會顯著增大殼體的總質量，但是對系統剛度的影響并不明顯。因此，增大蜂窩壁厚會降低系統的固有頻率。

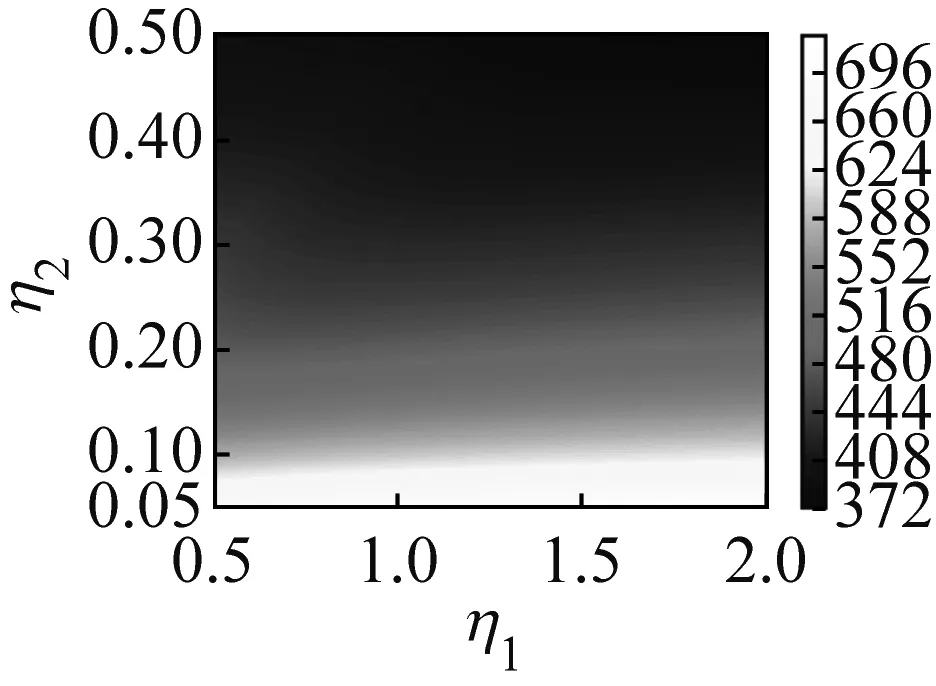
(a)第1階

2.2.3 胞元角度及鋪層方向

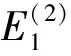
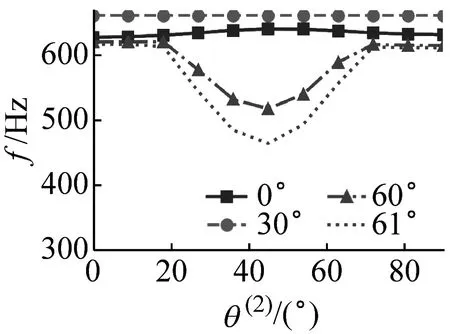
(a)第1階

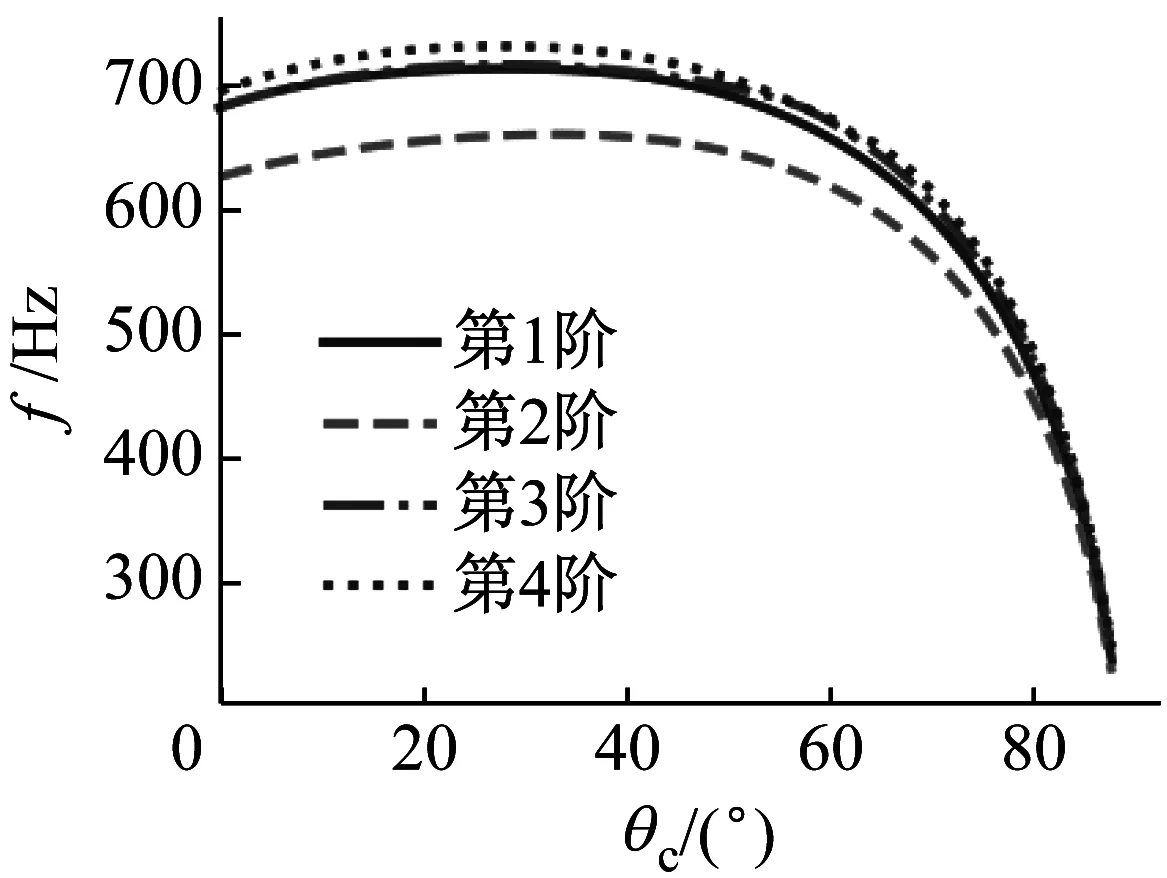
圖8 固有頻率隨θc的變化關系

3 結 論

針對具有彈性地基的復雜形狀蜂窩夾層殼體，通過一階剪切變形理論和改進的Gibson公式建立了系統的能量泛函，并利用哈密頓原理給出了其控制方程。利用改進傅里葉法對控制方程進行求解，并通過數值算例驗證此方法的快速性和可靠性。隨后，基于給出的模型，通過變參數計算揭示了蜂窩芯層各參數對系統動力學特性的影響規律。得到以下結論：

(1)當芯層厚度較小時，系統固有頻率隨芯層厚度比的變化關系取決于彈性地基剛度值的大小;當芯層厚度較大時，系統固有頻率隨芯層厚度比地增大而迅速降低。

(2)蜂窩胞元邊長比對系統固有頻率的影響并不明顯，但是增大蜂窩壁厚會使得系統的固有頻率顯著降低。

(3)系統固有頻率隨胞元角度地增大而先升高后降低，且當胞元角度較大且鋪層方向處于20°～60°時，其固有頻率對胞元角度的變化具有極高的敏感性。

附錄A

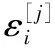
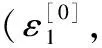
(A.1)

式中，T為位移-應變變換矩陣，將其展開有

(A.2)

(A.3)

(A.4)

(A.5)

(A.6)

附錄B

考慮殼體曲率的剛度系數矩陣RK為

(B.1)

其中

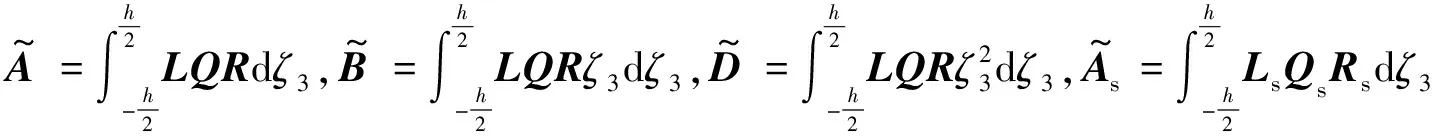
(B.2)

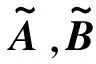
(B.3)

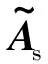
(B.4)

Κs為剪切修正因子，其表達式由文獻[20]給出。

附錄C

系統的廣義質量矩陣M可以寫為

(C.1)

其中

(C.2)

系統的廣義剛度矩陣K可以寫為

(C.3)

其中

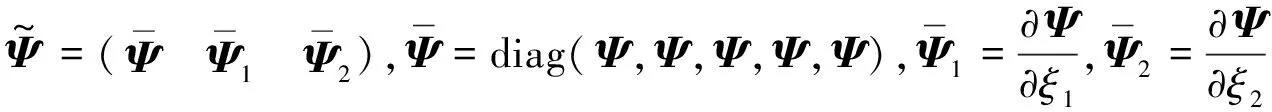
(C.4)