一溯到底，化“或然”為“必然”
——高中數(shù)學(xué)問題“怎么想”

◎ 海南省海口市海南華僑中學(xué) 鄧建書

中學(xué)數(shù)學(xué)教材中有很多問題，講解之后學(xué)生一般都能聽明白，但是過了一段時間之后，再次問到此類問題的解題方法和思路時，學(xué)生往往一臉茫然。作為教師，教學(xué)生“怎么思考”“怎樣才能想到”是數(shù)學(xué)教學(xué)的首要任務(wù)。筆者通過歸納高中數(shù)學(xué)教材的常見問題，追本溯源，化“或然”為“必然”，給學(xué)生提供思考的模式或方法。

方式一：從理論中“溯源”

很多實際問題可以從一般情況出發(fā)，先證一般情況（理論），再到具體情況，解決了一般情況，具體問題也會迎刃而解。比如因式分解中的“溯源”：初高中銜接課程中，因式分解很是關(guān)鍵，特別是高次多項式問題怎么分解，始終是一個難點。老師一般采用分組分解，學(xué)生也很容易聽懂和接受，但真正到學(xué)生自己來分解時，往往思索再三，仍無法區(qū)分清楚“或然”和“必然”。

其實，對于此類問題，高等代數(shù)課本中早已給出了答案：

定理：設(shè)f(x)=anxn+an-1xn-1+…+a1x+a0是一個整系數(shù)多項式，而r/s是它的一個有理根，其中r、s互素，那么必有s|an，r|a0特別地，如果f(x)的首項系數(shù)an=1，那么f(x)的有理根都是整根，而且是a0的因子。簡單地說，若此多項式有有理根，則其有理根必在

應(yīng)用此法，則可隨意組合，例如因式分解：

x3+9+3x2+3x，此題常規(guī)做法為分組分解：

x3+9+3x2+3x=x3+3x2+3x+9=x2(x+3)+3(x+3)=(x+3)(x2+3)，但學(xué)生的問題是：為什么要這樣組合？上面的定理即可打開疑團。

至此眼界已開，一般意義上的方法都已盡收眼底，知道-3是其一有理根，故有公因式(x+3)，后面的分組分解，思路一目了然了。

練習(xí)：因式分解x3-2x+1，易知其一根為1，故有公因式（x-1）。

評注：此題當(dāng)知道有一根是1時，想怎么組合都可以，關(guān)鍵是找到公因式（x-1）即可。運用添項、拆項法尋找目標(biāo)，有目標(biāo)就能打開思路，快速解題。教師講解清楚了，學(xué)生也很容易學(xué)會，從而對此類問題就可以心中有數(shù)，不再迷茫。

很多時候?qū)τ谝坏李}用一種方法解答后，應(yīng)該反思還有無其他簡單的方法，如果每次都這樣做，學(xué)生將受益匪淺。這樣才是高效學(xué)習(xí)，也是每位高中生應(yīng)該掌握的學(xué)習(xí)方法。

方式二：從數(shù)中“溯”形

通過仔細(xì)觀察和鑒別，找出數(shù)中形的“軌跡”，從形中找出解決問題的方法，思路也就自然打開。根據(jù)題設(shè)條件正確繪制出相應(yīng)的圖形，使圖形充分反映出相應(yīng)的數(shù)量關(guān)系，找出數(shù)與式的本質(zhì)特征。

比如：兩角差的余弦公式的推導(dǎo)和證明cos(α-β)=cosαcosβ+sinαsinβ。

觀察此公式：左邊是兩角差的余弦，右邊是這兩角的余弦和正弦，所以該如何構(gòu)造這兩角的余弦和正弦，可參考《數(shù)學(xué)必修第一冊》215頁的證明方法：

設(shè)單位圓與x軸正半軸相交于點A(1,0)，以x軸非負(fù)半軸為始邊作角α、β、α-β，它們的終邊分別與單位圓相交于點P1(cosα,sinα)；A1(cosβ,sinβ)；P(cos（α-β），sin（α-β））

連接A1、P1,則易證A1P1=AP，再用兩點間距離公式將左右等式連接起來。

余弦定理學(xué)生很容易想到用向量的數(shù)量積來證明，但正弦定理是如何通過向量來證明的呢？其實細(xì)想起來一樣可以用向量的數(shù)量積來證明，只不過要通過作垂直向量構(gòu)造角的余角,再通過誘導(dǎo)公式將余弦轉(zhuǎn)化為正弦。

圖1

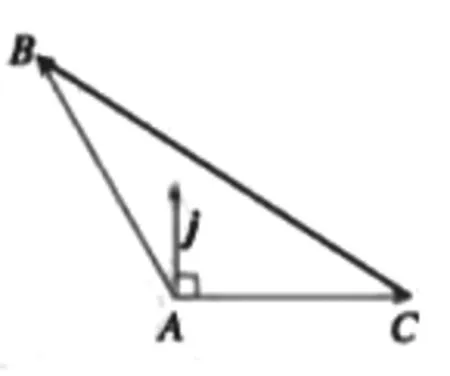
圖2

再如，選擇性必修第一冊第80頁：已知0＜x＜1；0＜y＜1，求證：

方式三：從形中“溯”數(shù)

從具體圖形中挖掘數(shù)的“軌跡”，通過數(shù)的運算達(dá)到形的需要。借助所給的圖形，仔細(xì)觀察、分析并歸納，找出圖形中蘊含的數(shù)量關(guān)系，反映幾何圖形內(nèi)在的屬性。

比如在立體幾何中關(guān)于正余弦定理的應(yīng)用：

已知二面角α-CD-β的平面角為120o，二面角內(nèi)一點P,到面α、β的距離分別為PA=2，PB=3,求點P到棱CD的距離。

解：（如圖3）因為PA⊥α，PB⊥β所以PA⊥CD，PB⊥CD，故CD⊥面PAB,設(shè)面PAB∩CD=O，則CD⊥OA，CD⊥OB，CD⊥PO，因此∠AOB=120o，且P、A、O、B四點共圓，∠APB=60o。

圖3

評注：解法一從宏觀上把握，眼觀六路，識別出PO為△PAB外接圓的直徑，輕松運用正余弦定理解之；解法二從解三角形的角度出發(fā)，利用兩個三角形的公共邊及相鄰角之間的聯(lián)系，巧用等式求角，再求邊長！

根據(jù)“數(shù)”與“形”既對立又統(tǒng)一的特征，觀察圖形的形狀，分析數(shù)與式的結(jié)構(gòu)，產(chǎn)生聯(lián)想，適時將它們相互轉(zhuǎn)換，化抽象為直觀，并找出隱含的數(shù)量關(guān)系。如此，則思路清晰，解答自然。

數(shù)形結(jié)合，主要指的是數(shù)與形之間的一一對應(yīng)關(guān)系；數(shù)形結(jié)合思想，就是把抽象的數(shù)學(xué)語言、數(shù)量關(guān)系與直觀的幾何圖形、位置關(guān)系結(jié)合起來，通過“以形助數(shù)”或“以數(shù)解形”，即通過抽象思維與形象思維的有機結(jié)合，將復(fù)雜的問題簡單化、抽象的問題具體化，從而實現(xiàn)優(yōu)化解題途徑的目的。

方式四：從綜合中追溯

一個問題通常有多種方式可以解決，所以充分調(diào)動所學(xué)知識，為解決問題提供多種方法，也為構(gòu)造系統(tǒng)化的知識鏈打下良好的基礎(chǔ)。比如中線長公式推導(dǎo)與證明。

圖4

圖5

（必修2 3.3.2例4）證明平行四邊形四條邊的平方和等于兩條對角線的平方和（坐標(biāo)法證明）。

（必修2習(xí)題4.2A組8）Rt△ABC中，斜邊BC為m。以BC的中點O為圓心，作半徑為n（n＜m/2）的圓分別交BC于P、Q兩點，求證：|AP|2+|AQ|2+|PQ|2為定值。（中線長公式的精彩應(yīng)用）

以上對于同一問題，可以從不同的角度來分析和證明，充分回顧和總結(jié)所學(xué)知識，發(fā)展思維能力。

方式五：從方法中“溯源”

很多時候，方法基本固定，掌握這些方法，問題也會輕松化解。

如：等差數(shù)列前n項和（倒序相加)利用等差數(shù)列性質(zhì)——下標(biāo)和相等，則相應(yīng)項的和相等；

等比數(shù)列前n項和（錯位相減)利用等比數(shù)列性質(zhì)，后一項等于前一項乘以公比，求和相減后，中間相同項抵消。

《教學(xué)課程標(biāo)準(zhǔn)》明確指出：“加強數(shù)學(xué)思想方法在進(jìn)行數(shù)學(xué)思考和解決問題中的作用，引導(dǎo)學(xué)生從解題的思想和方法上考慮問題，達(dá)到巧妙解題”。可見，數(shù)學(xué)思想和方法教學(xué)不容忽視，素質(zhì)教育下的數(shù)學(xué)教學(xué)更注重數(shù)學(xué)品質(zhì)的培養(yǎng)和邏輯思維能力的提高。其實，數(shù)學(xué)問題的解決過程就是用“不變”的數(shù)學(xué)思想和方法去解決不斷“變換”的數(shù)學(xué)命題，這既是滲透的目的，也是走出題海的重要環(huán)節(jié)。

方式六：從定理中“溯源”

比如證明立體幾何問題，通常以基本定理作為基礎(chǔ)，可以證明很多相關(guān)問題。

如《數(shù)學(xué)必修第二冊》163頁第10題：已知平面α、β、γ，且α⊥γ、β⊥γ、α∩β=ι，求證：ι⊥γ。

要證明線面垂直，得證此線垂直于平面內(nèi)兩相交直線，題中沒有這兩條直線，所以需要我們自己來構(gòu)造，設(shè)α∩γ=α，β∩γ=b，在γ內(nèi)取一點P分別作PA⊥α于A,PB⊥b于B,則兩條相交直線就找到了，如果題目中條件不夠，則需要自己創(chuàng)造條件。

通過以上事例說明，當(dāng)思維受阻時，不妨從源頭思考，從定義或已經(jīng)學(xué)過的知識中搜尋，一溯到底。也許這種“回到起點”的方式，能迅速打開思路。教師可以啟發(fā)學(xué)生用提示語探究，不僅在解題時，更需要在新授課教學(xué)中運用。

加強對數(shù)學(xué)整體性的認(rèn)識，強調(diào)以具有整體性的知識單元為載體，從知識的聯(lián)系性出發(fā)進(jìn)行教學(xué)設(shè)計并開展課堂教學(xué)，是新一輪課改的顯著特點。究其原因，主要是長期以來，在高考評價“唯分論”指揮棒下的數(shù)學(xué)教學(xué)，多采用“灌輸+記憶”的方式強加給學(xué)生，再通過刷題提高解題技巧“秒殺”高考題，可以提高分?jǐn)?shù)，但不利于學(xué)生獲得“四基”、提升“四能”，不利于提高學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣。為此，基于全面實現(xiàn)數(shù)學(xué)育人目標(biāo)的教學(xué)，必須強調(diào)數(shù)學(xué)的整體性、邏輯的連貫性、思想的一致性、方法的普適性及思維的系統(tǒng)性，這樣才能充分調(diào)動學(xué)生思維的積極性，引導(dǎo)學(xué)生感受數(shù)學(xué)的美好，愛上數(shù)學(xué)，從而為學(xué)好數(shù)學(xué)而努力。