汽車輪輻型面特征對車輪的氣動特性影響分析

童 一，張 丹，貝紹軼，張 亞，鄭 焱

（江蘇理工學院 汽車與交通工程學院，江蘇 常州 213001）

當前，我國采取了許多措施推進節能減排，汽車產業節能減耗、低碳發展勢在必行。作為影響車輛能耗的一個基本參數，空氣阻力的減少可直接降低整車的燃料消耗。有研究表明，汽車車輪產生的空氣阻力占整車空氣阻力的25%，因此，車輪空氣動力學一直是學術界和工業研究中的重點。

楊志剛等人[1]采用CFD（計算流體動力學）的方法，對靜止和旋轉孤立車輪局部流場進行研究，并通過試驗驗證了車輪的旋轉會對流場產生巨大影響；Diasinos等人[2]通過對不同結構車輪旋轉狀態下尾跡的氣動特性分析，發現幾何形狀的變化可以改變流動細節；谷正氣等人[3]通過改變車輪輪輻開孔大小和開孔數量，分析了其對整車氣動阻力的影響；蘇暢等人[4]利用Fluent軟件，探究了不同輪輻偏移距離及曲率與整車氣動阻力系數的關系；沙強等人[5]在輪轂形態設計中加入參數化設計方法，通過合理組合點、線、面與基本形體、骨骼線，使輪轂結構協調統一且設計合理。上述研究發現，合理的輪輻外形設計，對降低車輪氣動阻力十分重要。

除此之外，Hobeika等人[6]對獨立旋轉車輪條件設置進行研究，在具有強烈旋轉效應區域引入MRF域，實現獨立旋轉車輪的正確模擬；方健等人[7]對旋轉車輪的輪輞采用不同的封堵比例，發現輪輻開口可降低風阻，減阻貢獻由輪心向外逐漸增強；傅立敏等人[8]通過模擬和試驗結果對比，驗證了車輪的幾何外形在數值模擬中對汽車空氣動力學特性的影響十分顯著，應予以充分考慮。

然而，對于如何在滿足工程可行性并保證造型美觀的前提下，進行輪輻型面設計，使其具備良好的氣動特性，目前還缺少相關研究。因此，本文針對幾種正面造型設計出不同輪輻型面的車輪，通過數值模擬，探究不同輪輻型面對車輪氣動阻力系數的影響，揭示其減阻原因，從而為低風阻車輪輪輻型面設計提供一定參考。

1 模型建立

1.1 車輪幾何模型

選取某小型轎車車輪，輪胎型號為175/50R15。由于輪胎凹坑的非光滑結構會影響其壁面附近的流體運動[9]，因此，為了避免對本文分析產生影響，將車輪輪胎均更換為光面輪胎。如圖1所示，針對五輻車輪，三種正面造型分別為直線型面（A型）、折線型面（B型）以及弧線型面（C型），對車輪輪輻面進行簡化處理，構建出三種不同輪輻型面的車輪。在標準車輪簡化模型中，固定不同型面的車輪開孔比例為42%，輪輞最外側所在平面距輪輻中心面的水平距離為0，以避免開孔比例與水平距離的不同對分析結果產生影響。

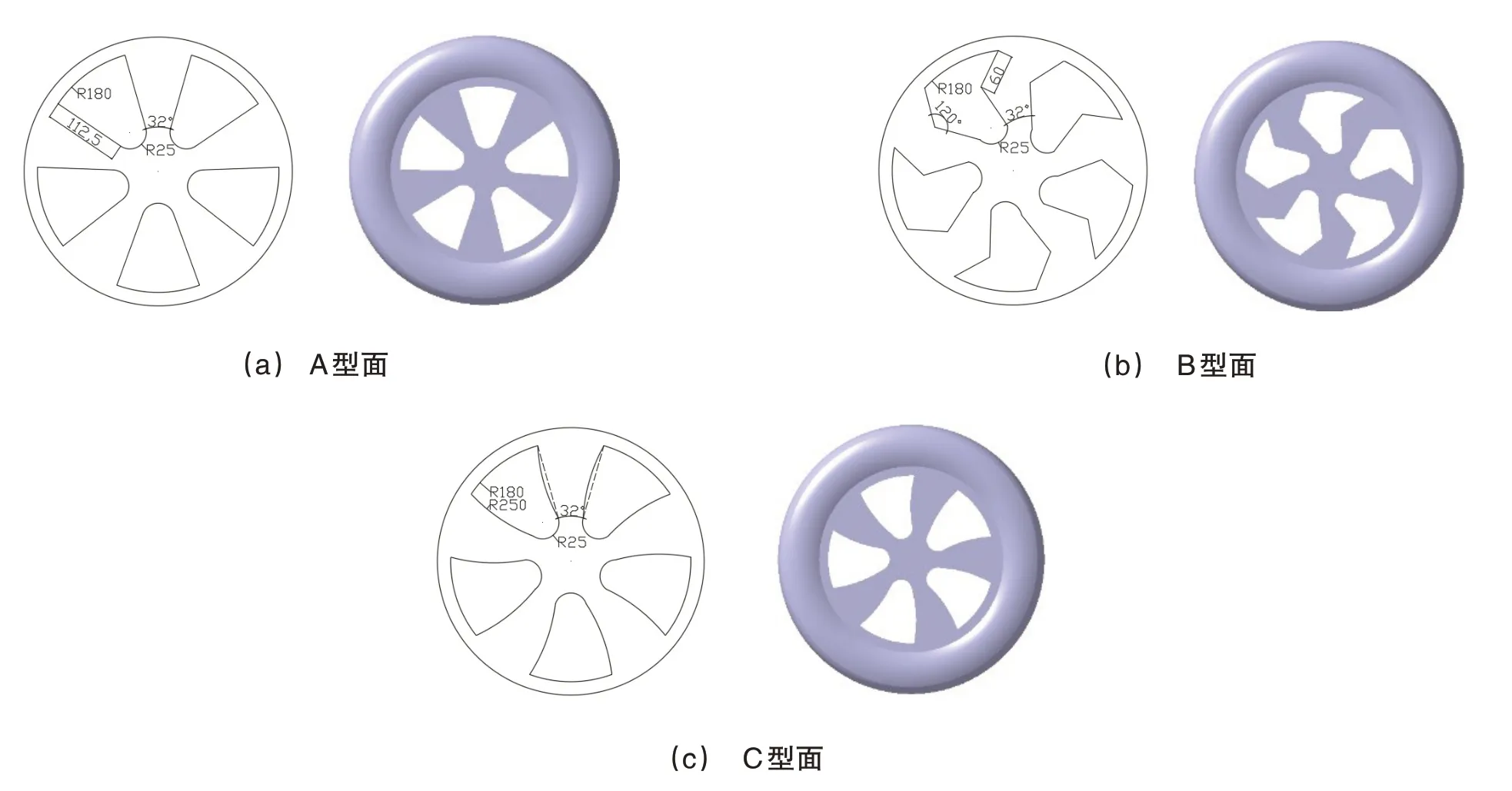
圖1 車輪輪輻型面幾何形狀

1.2 計算域及網格劃分

如圖2所示，為計算域示意圖。車輪數值模擬的計算域需要設置與實際狀態相近的邊界條件，具體長度見圖2。通過對計算域的合理選擇，可以忽略計算域邊界（頂面和側面）對流場的干涉。

在生成可以計算的體網格之前，需要對車輪幾何模型進行表面處理以及拓撲檢測，以避免交界面不閉合、曲線重復、曲面不閉合等問題；同時，考慮到分析獨立車輪的精度要求，需要將車輪面網格劃分得更加細膩。如圖3所示，本文選取將車輪面網格劃分為4 mm。

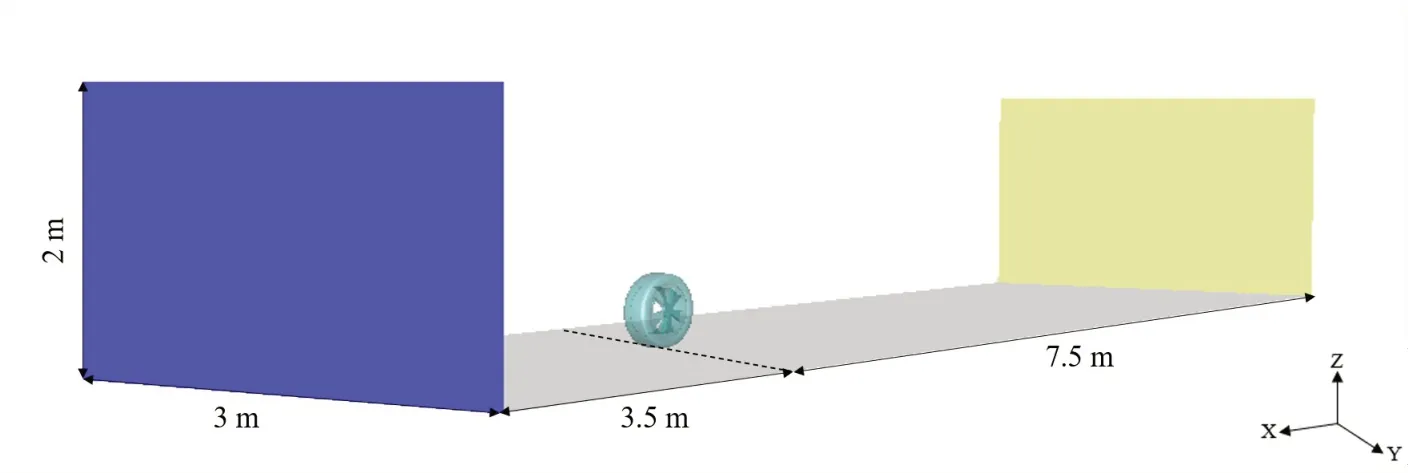
圖2 計算域示意圖

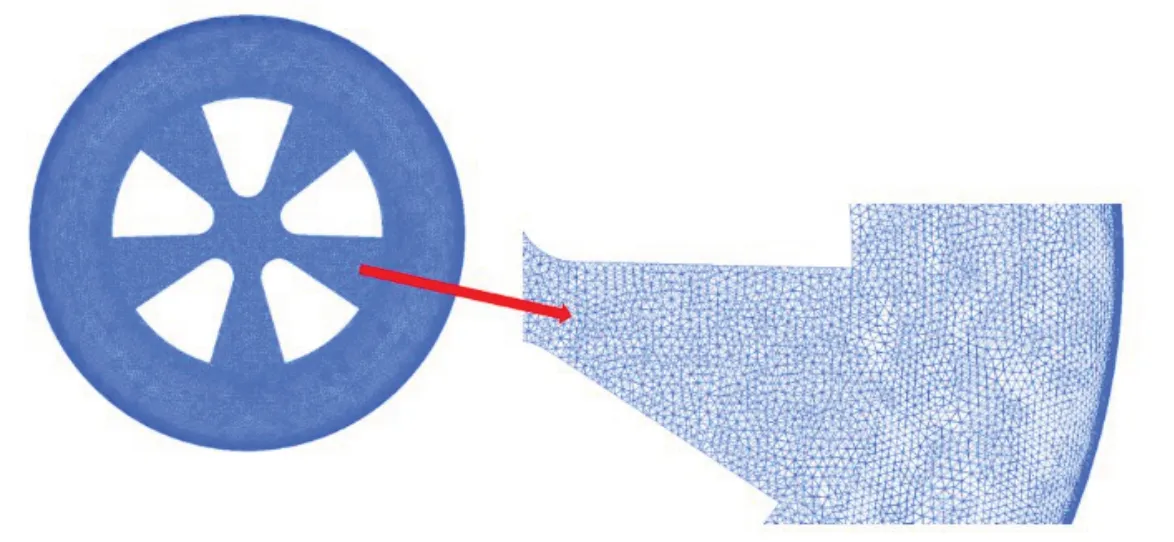
圖3 車輪面網格

由于車輪的外流場主要受輪腔和車輪自身的影響，因此，為了精確地求解車輪周圍的流場，應采用不同的密度盒使轉動車輪周圍的網格尺寸變小。在合適的網格數量下，能夠保證旋轉車輪周圍的網格質量。本文采用三層加密策略：第一層加密區域網格大小為6 mm；第二層加密區域網格大小為12 mm；第三層加密區域網格大小為30 mm。同時，在近壁面設置邊界層，邊界層第一層厚度為1 mm，共5層，網格量控制在合理范圍內。

如圖4所示，為最后形成的加密區域（密度盒1、密度盒2和密度盒3）。

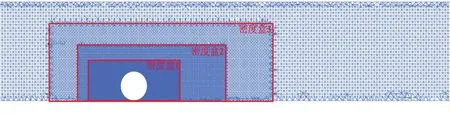
圖4 旋轉車輪計算域設置

1.3 計算方法及邊界條件設置

利用ANSYSFLUENT軟件，基于分離壓力的求解器計算，離散方法選擇二階迎風；同時，選擇用于壓力-速度耦合的標準SIMPLEC算法。車輪旋轉時的局部密度變化，特別是靠近地面區域的變化，可能對流動有輕微影響，而空氣屬于不可壓縮范圍；所以，計算模型可選擇三維定常不可壓縮粘性流動，采用三維不可壓縮雷諾平均N-S方程，流場計算選用RNGk-ε湍流模型[10]。相較于標準k-ε模型，RNGk-ε湍流模型可以更好地處理高應變率及流線彎曲程度較大的流動。

計算域入口為速度入口，出口采用壓力出口，計算域頂面及側面為固定無滑移壁面，地面為移動無滑移壁面[11]。為了在模擬中將車輪的旋轉這一實際問題考慮在內，使仿真模擬更加接近真實情況，將車輪設置成多參考坐標系旋轉壁面（MRF）條件。如表1所示，為具體邊界條件。

表1 仿真邊界條件設置

1.4 網格無關性驗證

為了更好地模擬車輪旋轉時表面及周圍的流場狀態，同時節約計算時間，對A型面車輪的網格采用了不同的加密方案。如表2所示，為仿真模擬后的計算結果。由表2可知，8.2×106的網格計算結果與1.2×107的網格計算基本一致，Cd值已經達到穩定。為節省資源和計算時間，三種不同型面的網格劃分均采用A-2加密方案，計算模型均采用8.2×106左右的網格數量。

表2 網格無關性驗證

2 計算結果比較與分析

2.1 氣動力分析

在輪輻開口面積相同的情況下，改變不同型面。如圖5所示，為三種不同型面車輪氣動阻力系數和升力系數。由圖5可見：B型面車輪氣動阻力最大；C型面車輪氣動阻力最小，相較于另外兩種型面車輪，其氣動阻力分別減小約1.6%、5.7%，而不同型面引起的升力變化近乎于0。

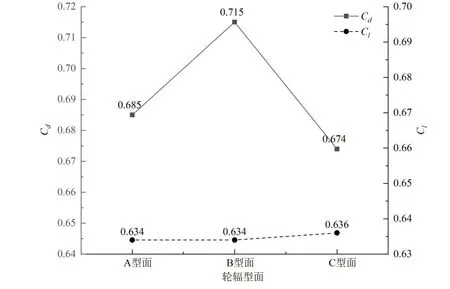
圖5 不同輪輻型面氣動阻力系數和升力系數

2.2 壓力分析

如圖6所示，為不同型面車輪中心線平均壓力系數曲線。三個不同型面車輪最大正壓系數值都在1.0處，最大負壓均出現在270°附近，這與英國達勒姆大學的Mears等人的研究趨勢相似。車輪頂部270°附近最低壓力系數處，被稱為負壓峰值。由圖6可知，三種不同輪輻型面車輪在尾部（100°~270°）區域，平均壓力系數Cp分布幾乎相同，其差異和空氣動力特性主要取決于雷諾數和車輪形狀（縱橫比和胎肩）。

如圖7所示，為X=0.52D處各車輪垂直高度壓力分布曲線。其中：X表示距離車輪中心的水平距離；D表示車輪的直徑。在各車輪后X=0.52D處設置壓力系數提取探測線，以查看車輪后部的壓力變化。根據圖7可以看出：貼近地面處均為正壓，遠離地面處Cp值近乎為0，由地面向上三個車輪的壓力變化都呈現先減小后增加的趨勢；在車輪尾部X/D=0.52的相同高度處，C型面車輪的壓力系數要高于其他兩個型面的車輪，可見，C型面車輪其尾部的低壓中心相對于其他兩個型面，距離旋轉車輪尾部更遠，從而降低了車輪的氣動阻力。

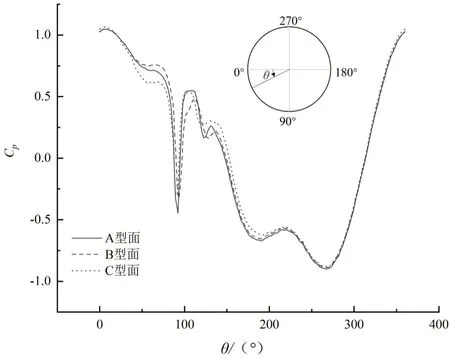
圖6 車輪模型中心線平均壓力系數Cp分布

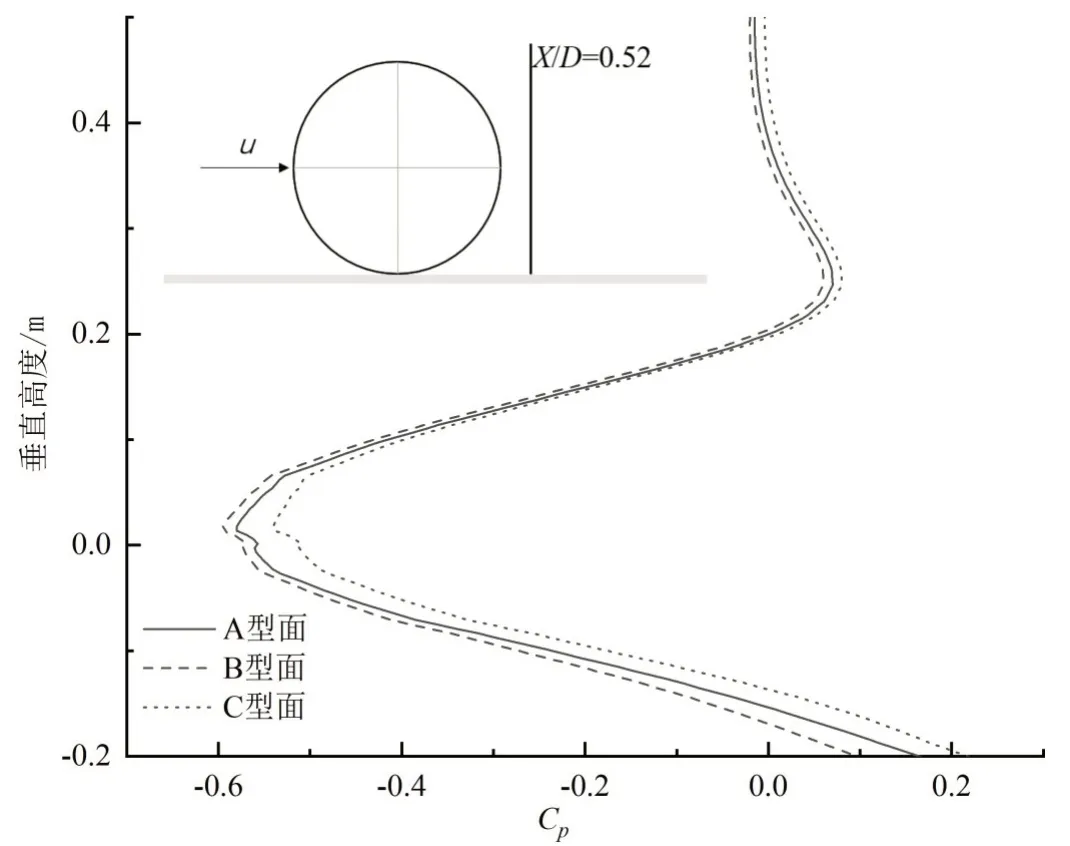
圖7 X/D=0.52處各車輪垂直高度壓力分布曲線

如圖8所示，為X=0截面壓力云圖。從圖8可以看出，輪腔內部壓力差異很大：C型面車輪的輪腔內部壓力接近于0，在輪腔靠近地面處形成了一個較小的渦；而A型面和B型面的車輪均在輪腔中央形成了一個穩定的低壓渦；對比三個型面，B型面車輪形成的低壓區要明顯大于其他兩種型面。

渦是湍流場中消耗能量的主要方式之一，也是氣動阻力的一個主要來源，渦的結構不同，對氣動阻力的影響也有大小。如圖9所示，為車輪中心對稱面壓力云圖。可以看出，中心對稱面處輪腔內的渦結構區別很大：A、B型面的車輪在輪腔中心各有一個穩定發展的渦，輪腔內的穩定渦造成了大量的能量耗散；C型面車輪并沒有在中心部位形成一個穩定的渦，這也是C型面車輪阻力小于其他兩個型面的原因。結合圖8和圖9可以發現，不同型面所導致的輪腔內渦結構差異，是引起車輪氣動阻力差異的主要原因。

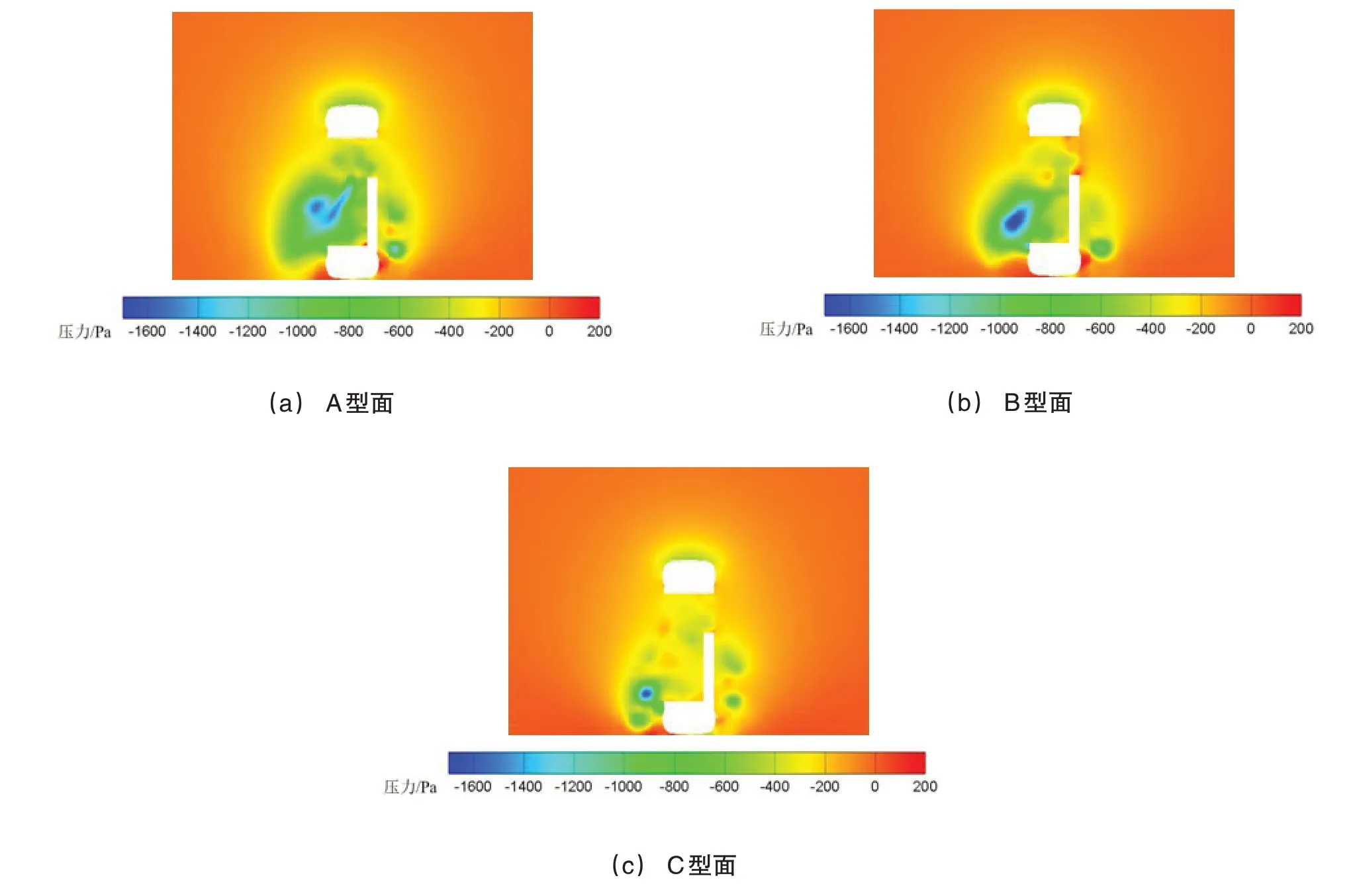
圖8 X=0截面壓力云圖

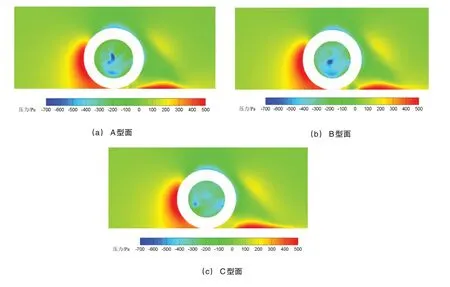
圖9 車輪中心對稱面壓力云圖

2.3 不同型面車輪表面速度

如圖10所示，為車輪表面速度云圖。根據圖10可以看出：C型面車輪正面輪胎及輪輻的表面速度均高于其他兩種型面，使輪輻開口處氣流更難流入輪腔內，輪輻外側的氣流較快地沿著輪輻外側切線流過；B型面車輪表面速度最低，更多氣流由開孔處進入輪腔內側；分析不同車輪型面引起的輪腔內負壓區域的大小，得到：B型面>A型面>C型面，即造成氣體進入輪腔多少的主要原因是壓差；B型面內部負壓渦最大，使得氣體被吸入輪腔內部，加劇了車輪輪腔內部復雜氣流擾動，從而使旋轉車輪能量損失增大。

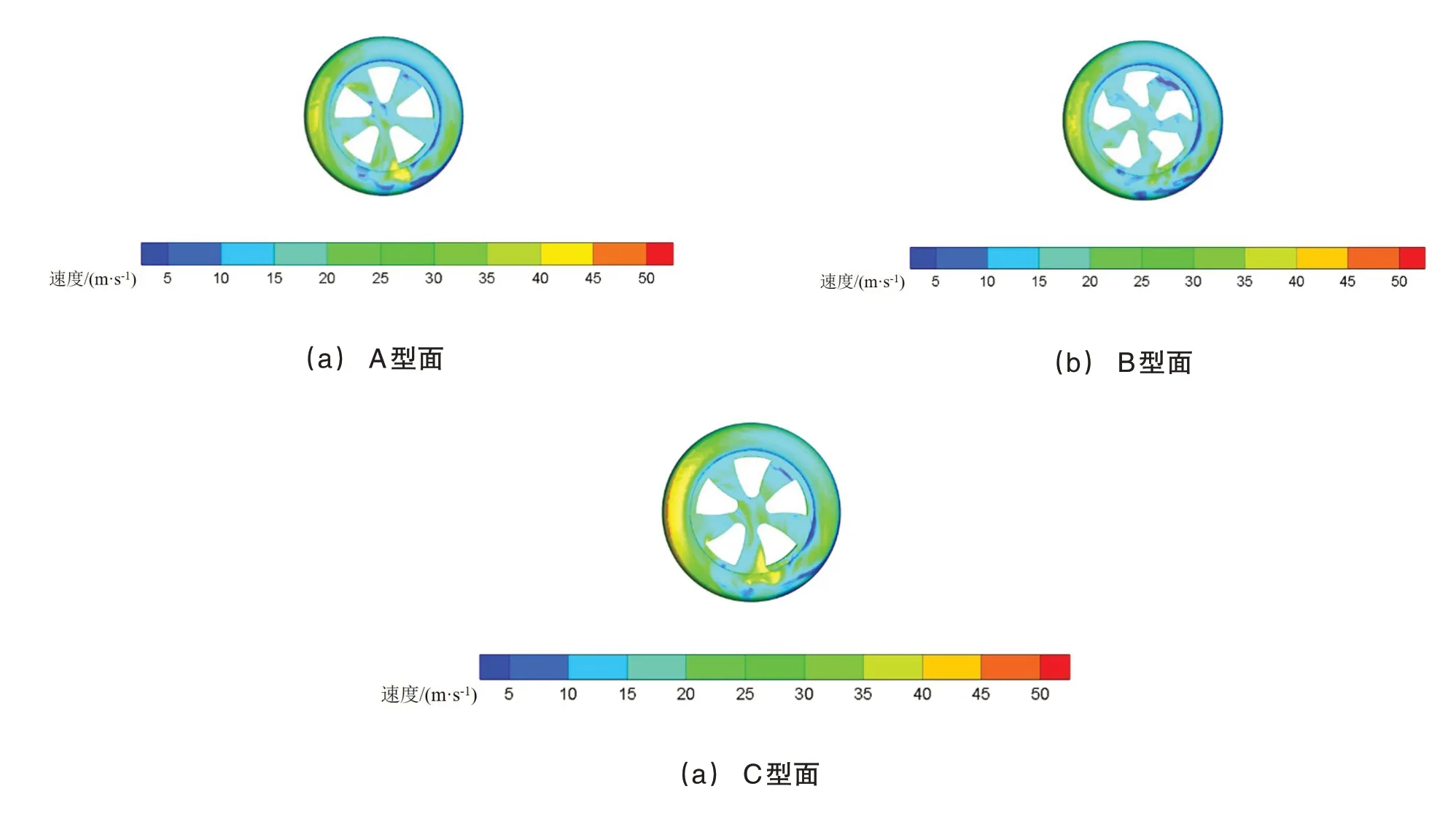
圖10 三種型面車輪表面速度云圖

2.4 不同型面車輪速度流線

如圖11所示，為A、B、C三種型面車輪速度流線，可以比較直觀地看出車輪輪腔內氣流對車輪氣動阻力的影響。圖中圈出B型面的流線密度相較于其他兩個型面明顯最大，對于不可壓縮流體，流線越密集，流速越大，說明B型面輪腔內部區域的氣流擾動情況最為劇烈。

由圖11可知：C型面車輪輪輻外側氣流流入輪腔內流速最慢，所以C型面輪腔內氣流擾動相較于其他兩個型面較小，雖然也有一個渦，但其渦結構與其他兩個型面相比尺寸明顯較小；B型面車輪輪腔內有一個穩定發展的渦旋，而且渦最強烈，所以B型面車輪引起的氣動阻力最大。不同型面車輪的氣流均由輪輻面進入輪腔，最終通過輪腔內側靠近地面處流出。

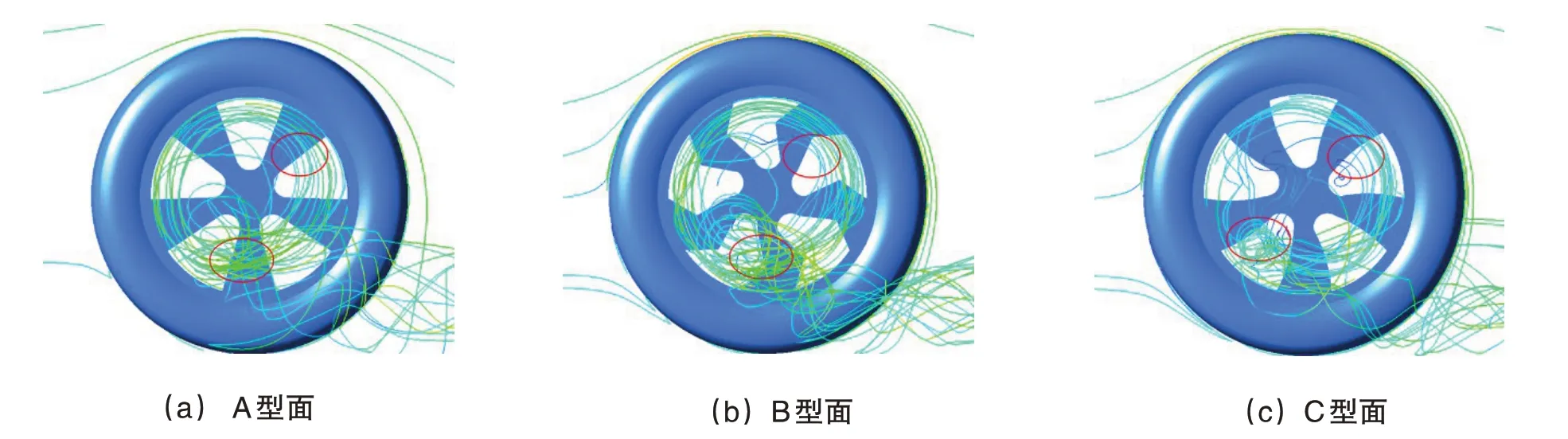
圖11 三種型面車輪速度流線

3 結論

本文采用RNGk-ε湍流模型，對獨立車輪外流場進行三維數值模擬，對比分析了正常工況下三種獨立車輪的氣動特性，得到以下結論：

（1）總開口面積相同的車輪輪輻，弧線型面有良好的減阻效果，相較于直線和折線型面車輪，其風阻系數分別降低了1.6%和5.6%。

（2）不同車輪輪輻型面直接影響了氣體在輪腔內的流動，從而表現出氣動力方面的差異；因此，對于輪輻造型設計方面的研究，不僅需要考慮開口面積，還需要考慮不同型面形狀對輪腔內氣流流動特征的影響。輪輻型面的差異最終會影響車輪的尾流結構和氣動特性。