基于多目標差分進化算法的機場停機位分配問題研究*

羅聿倫

（東北大學秦皇島分校，河北秦皇島 066004）

1 研究背景與意義

進入21世紀，隨著民航業的高速發展，航班數量快速增長與停機位數量增長緩慢的矛盾日益突出。2018年中國民航行業發展統計公報顯示，當年全國民航運輸旅客數量和航班數量增長速度(10.2%、8.2%)遠遠超過了停機位數量的增長速度(5.5%)，［1］給機場運行帶來了巨大壓力。許多繁忙的機場停機位數量有限，不夠合理的手工編排停機位又加劇了停機位緊張的局面。

要想解決停機位數量不足的問題，如果僅增加停機位數量，所需時間長，費用高，無法從根本上解決問題。而提出更好的停機位分配方案，經濟成本和時間成本都較低，可以盡可能地增大飛機的靠橋率，減少旅客轉移時間，提高旅客滿意度和機場運行效率。目前，國內外對停機位分配問題的研究，方法、角度很多，Braaksma等人和Haghani等人在研究停機位分配時將旅客最小步行距離作為優化目標。［2-3］李倩雯以航班靠橋率最大為優化目標，建立基于機場實際運行情況的停機位分配模型。［4］鄭攀以提高機場運行效率為出發點，提出基于航班從起降跑道至所在區域的滑行距離最小化來建立模型。［5］周曉寧等人在建立模型和設計方案時考慮了降低航空排放和近機位利用率。［6］歸根結底，機場停機位分配問題也是一個在一定約束范圍內的多目標優化問題。優化目標不同，對應的最優分配方案也有所區別，因而從拓展差分進化算法的角度分析進一步優化機場停機位分配方案，具有很強的實用性。

2 停機位分配的約束條件

機場的停機位分配問題，又稱停機位指派問題。主要是指在一定的時間范圍內，已知預降航班的屬性，以及機場停機位運行條件的情況下，由機場指揮運行中心進行及時、合理的決策，為航班分配對應的停機位。對停機位進行合理的分配是航班安全高效運輸的保證。停機位分配時需要遵循基本的分配規則，會受到一定條件的制約。主要有以下幾點：航班降落時，至少有一個不小于飛機機型等級的空閑停機位；每個停機位在航班降落至離開停機位滑行的這段時間內，停靠的航班數量≤1；經停航班應有充足的停靠時間，即一架飛機進入到離開停機位的時間，應保證完成地面作業；為保障飛行安全，避免沖突事故，分配到相同停機位的上一出港航班和下一進港航班需要有時間間隔；為提高機場運行效率，機型與停機位應當相互匹配，中小型飛機應避免占用更大機型的停機位。除以上約束條件外，設定不同的優化目標時對應的條件也有所差異，在此不再逐一論述，建立停機位分配模型的約束條件需要正確選取。通過這些約束條件的分析，我們明確了分配時應注意的限制因素，從而為停機位分配模型的建立奠定基礎。

3 建立停機位分配模型

在繁忙的大中型機場里，航班數量和停機位的數量都很多，單憑管理人員的經驗來手工編排停機位分配方案很難達到較高的效率，甚至會帶來安全隱患。經過與南寧吳圩國際機場的管理人員交流得知，傳統的手工編排停機位通常是將旅客人數最多的飛機分配給最佳停機位，再依照旅客數量依次分配剩余航班。雖然這樣分配是一種解決問題的邏輯方法，但此方法通常無法提供最佳分配方案。

在此舉一個簡單的例子來說明為什么傳統的分配方法可能不夠理想。［7］根據表1中顯示的示例航班時刻表，某日上午，一架波音747型飛機和3架波音737型飛機先后抵達某機場。預分配的停機位有A和B兩個，停機位對應的步行距離在表2。因為波音747上的旅客較多，且停機位A對應的旅客步行距離較短，手工編排停機位會將等級較高的波音747分配到停機位A，三架波音737被分配到B。但是，由于波音747停靠在最佳停機位的時間太長，且旅客數量少于三架波音737之和，因此表3給出的最佳分配方案是將波音747分配到停機位B而將三架波音737分配到停機位A。傳統的分配方案不是最佳分配方案，若飛機和停機位的數量更多，傳統分配方法的效率會更低。

表1 示例航班時刻表

表2 停機位對應的步行距離單位：米

表3 停機位分配結果

鑒于傳統分配方法存在的缺陷，本文從最短旅客轉移時間和提高機場運行效率的目標出發，建立對應的數學模型。相較于傳統的直接計算步行距離和時間的方法，本文引入航班—機位分值矩陣（FS）和航班—航班分值矩陣（FF），將這些計算的對象和約束條件用加權分值的方法表示為矩陣中的元素，各分值由航空公司和機場指定。由于每個機場的布局和航班都不同，這樣的處理方法不需要在分析每個機場時都進行建模，提高了模型的通用性。模型中的目標函數如式（1）所示：

這一目標函數將停機位和航班匹配度分值和兩航班之間匹配度的分值分別求和再相加，總分值越大則停機位分配的方案越好。模型中各參數釋義如下：

f：所有航班的集合；

s：所有停機位的集合；

afs：航班—機位分值矩陣（FS）參數，以及表示航班f與停機位s的匹配度的加權分值，分值越高則航班f的旅客從停機位s至機場出口的轉移時長越短或機場運行效率越高；

bf1f2：航班-航班分值矩陣（FF）參數，表示兩架航班f1和f2被分配到同一停機位（相同航空公司的飛機盡量集中停放）的加權分值；

決策變量x fs的含義如式(2)所示：

本模型包含4個約束條件：（1）每架飛機只能停靠在一個停機位，（2）當FS矩陣中的afs＜0時表示此航班f不能分配至停機位s（如停機位和飛機等級或性質不匹配）；（3）當FF矩陣中的bf1f2＜0,時表示航班f1和f2不滿足上文約束條件，不能夠被同時分配至同一停機位；（4）決策變量x fs是0-1變量，各約束的數學描述如表4所示。

表4 模型中各約束的數學描述

本模型的建立貼合機場實際運行中所需的優化目標，在保證機場的高效運行和旅客的快速轉移中取得了平衡。另外，將前文列舉的優化目標和約束條件針對模型做出對應的調整，使全文更為連貫，且適合使用差分進化算法對模型進行求解。

4 差分進化算法的流程與改進

4.1 差分進化算法的原理

差分進化（DE）算法最早由Storn和Price在1995年提出，［8］它是一種基于進化思想和種群差異的超啟發式群智能最優化方法，其基本原理是通過種群中個體不斷的競爭和改良來求解最優化問題。主要包括生成隨機種群、變異、交叉、選擇等四項基本操作，使種群一代代進化，向最優解靠近，對目標函數的解進行優化。［9］對于非確定性較大的多目標優化問題，算法的搜索能力比傳統方法和手工計算都更強，更容易找到問題的最優解。

4.1.1 種群初始化

首先設置初始進化代數g=0，在優化問題的可行解范圍內按式(3)隨機產生NP個滿足約束條件的個體X構成初始種群。此外，在生成種群之前還需要設置的參數有最大迭代次數Gmax、縮放因子F和交叉概率CR。

為保證種群的多樣性，通常采用隨機函數來生成初始種群，每個個體表示問題的一個解，D表示向量的維數。

4.1.2 變異操作

變異操作源自生物學中染色體的基因突變，是DE算法的關鍵步驟。經過種群初始化后，從生成的種群中隨機選擇兩個父代個體（向量）由式(4)生成差分矢量,再將其增加給另一個父代個體矢量，由式(5)產生一個子代個體變異矢量。操作過程如圖1所示：

縮放因子F是DE算法的三大關鍵控制參數之一，控制差異矢量的搜索步長。這一步驟在父代的基向量上增加一個隨機偏差擾動。在標準DE算法中，進化早期各個體之間差異較大，F可使算法前期擁有較強的勘探能力和全局搜索能力。進化到后期算法的搜索速度加快，提高了搜索效率。

4.1.3 交叉操作

交叉操作是指變異操作產生的個體與父代種群中的其他個體進行分量上的交叉，得到子代個體，保證了種群進化的連續性和多樣性。交叉方式主要有二項式交叉和指數交叉兩種。大量實驗表明，二項式交叉通常比指數交叉擁有更優的求解性能且應用廣泛，因此本文的交叉操作采用二項式交叉的方式。操作方程為式(6)。

二項式操作式中uij,g是第g代中候選個體ui,g的第j維分量，它對應的在[0,1]之間均勻分布的隨機數rand(0,1)≤CR時就用變異個體對應的分量v ij,g代替它，否則就將父代個體分量x ij,g保留到下一代。jrand是第j維分量對應的系數，一般是序列[1，2，…，D]中的一個隨機整數。通過對每個變量都進行交叉，使子代個體對應的向量至少有一維分量為變異個體貢獻。

4.1.4 選擇操作

選擇操作是DE算法一個周期內的最后一步，即將經過交叉選擇后產生的子代個體ui,g+1與父代個體x i,g按式(7)進行適應度評價，適應度值較高的個體進入下一代進化程度更高的種群中，成為個體x i,g+1。

DE算法采用的是貪婪選擇的操作，即若當前的種群中個體對應的適應度較父代更優，該個體就在下一代種群中替換對應的父代個體，父代種群中的每個個體都會至少進行一次這樣的操作，這樣操作淘汰了原有種群中較差的個體，具有保留種群最優解和優勝劣汰的特點。

優化算法中控制參數的數量和設置的復雜程度關系到算法的性能高低。DE算法的控制參數相對較少，但這些參數對算法的全局搜索能力、局部搜索能力、收斂性能和魯棒性等性能指標影響較大，其中縮放因子F的影響最為顯著。當算法出現早熟收斂時，應增大NP和F的值。若算法的搜索速度過低，收斂困難，可以在不影響種群多樣性的前提下增大CR，減小NP和F的值。

4.2 經典差分進化算法的改進

通常情況下，在機場停機位分配問題中使用經典DE算法可以得到一組比手工編排停機位分配方案更優的解。然而，經典DE算法在求解復雜的多目標優化問題時也存在局限性，其求得的解未必是最優解，算法存在進一步優化的空間。因此，本文修改了經典DE算法的變異策略和控制參數，得到一種全新的改進DE算法，并在后文使用標準測試函數和停機位分配的仿真數據進行對比測試，驗證改進前后兩種算法的優劣。

本文所提出的是新的變異策略和參數自適應相結合的方法，在變異策略上，基于經典DE算法中搜索能力和收斂速度較為平衡的DE/rand-to-best/2策略(式（8）)提出了DE/rand-to-best5%/2策略(式（9）)：

算法原變異策略的搜索會逐步趨向于當前種群中的唯一最優解，但這一最優解很可能僅是局部最優解。經過改進后，算法的搜索趨向于種群中前5%的若干個優秀個體，能夠在算法搜索的過程中引入足夠的擾動，增大了跳出局部最優，找到全局最優解的可能性。

在控制參數的設定上，本文在經典DE算法中原有縮放因子F的基礎上，再引入一個新的縮放因子K。K和交叉概率因子CR均為自適應變化，各控制參數中的取值分別為從取值中可以看出，K和CR的值會隨著進化代數的增加不斷減小，使得迭代早期算法有較好的尋優能力，在算法運行到中后期時，擾動在的基礎上隨機增減(0，0.1)范圍內的一個隨機數，能夠使算法保持收斂速度和一定的擾動，不拘泥于現有種群內的最優解。而F的取值為常數，可以較好地保持種群多樣性。

5 實驗測試與結果分析

為了驗證算法性能，首先引入幾個標準測試函數對經典DE算法和改進后的DE算法進行測試。因為本文所建立的停機位分配模型，不需要機場實際運行中的航班數據，所以本節通過構造幾組停機位分配的仿真測試數據再次對改進前后的DE算法進行對比實驗，以驗證算法改進的有效性。

5.1 采用標準測試函數對算法進行測試

通過大規模計算分析法，選用收斂性指標作為性能標準對DE算法進行評價，主要包括收斂速度與收斂精度兩種，它們是評價算法性能高低的重要指標。本節選取了3個標準測試函數［10］，編寫相應程序，分別進行10次重復實驗來對比改進前后DE算法的性能。控制參數設置為：種群規模NP=40，維數D=20，最大迭代數Gmax=1000，經典DE算法的縮放因子F=0.4，交叉概率因子CR=0.5，改進后DE算法的縮放因子F=0.4，縮放因子交叉概率因子

5.1.1 測試函數1

函數名為First De Jong function(sphere)，圖像如圖2所示，表達式如式(10)所示：

該函數的最優解為0，測試結果如表5所示。

表5 First De Jong函數測試結果

5.1.2 測試函數2

函數名為Second De Jong function(Rosenbrock's saddle)，圖像如圖3所示，表達式如式(11)所示：

該函數的最優解為0，測試結果如表6所示。

表6 Second De Jong函數測試結果

5.1.3 測試函數3

函數名為Eggholder Function，圖像如圖4所示，表達式如式(12)所示：

該函數的最優解為-959.579672，測試結果如表7所示。

表7 Eggholder函數測試結果

從以上測試結果可以看出，無論是簡單還是復雜的目標函數，經過變異策略改進和參數自適應控制的DE算法在搜索速度和尋優能力上都要強于經典DE算法。也就是說，改進后的DE算法在求解復雜的多目標優化問題上更具優勢。

5.2 仿真測試的介紹

在實際測試開始之前，首先應該對設計的實驗加以介紹。以仿真實驗組1為例，這個實驗組中有6架飛機，編號1到6，5個停機位，編號1到5，則航班-機位分值矩陣（FS）和航班-航班分值矩陣（FF）如表8、表9所示。

表8 實驗組1航班-機位分值矩陣（FS）

表9 實驗組1航班-航班分值矩陣（FF）

在FS矩陣中，以飛機1為例，它與停機位1到6的加權分值分別為-15，20，…，10分，即這架飛機不能分配到停機位2和4，分配到停機位1是最佳分配方案。FF這個上三角矩陣代表兩架飛機相互關系的加權分值，飛機1和飛機2到6的加權分值分別為5，-10，…，-5分，即飛機1不能和飛機3，6分配到同一停機位，與飛機4分配到同一停機位是最佳分配方案。這兩個矩陣的元素在本次仿真測試時為自行構造，在實際的機場運行中則由機場管理部門和航空公司確定。

以實驗組1為例，算法運行的流程為：利用隨機數生成NP個5維個體，代表5架飛機，它們的取值范圍是(0,6)，即維數D代表飛機的數量。然后將生成的5個隨機數向上取整，每個個體就對應一個完整停機位分配方案。分別計算它們的FF、FS矩陣加權分值再求和，可以得到該方案目標函數的值。再使用差分進化算法不斷迭代，最后得到最高分值為問題的最優解。各實驗組分別進行10次仿真實驗來對比改進前后DE算法的性能。控制參數設置為：種群規模NP=40，維數D=飛機數量，最大迭代數Gmax=2500，經典DE算法的縮放因子F=0.4，交叉概率因子CR=0.5，改進后DE算法的縮放因子F=0.4，縮放因子交叉概率因隨機變量x取值上下限為(0，停機位數量)再向上取整，FF和FS矩陣加權分值的取值范圍是[-10,30]。

在機場的實際運行中，飛機的數量在大多數情況下都要大于停機位的數量，本文設置的實驗組中飛機和停機位的數量也遵循這一規則。另外，相較于使用標準測試函數進行測試來看，機場停機位分配的仿真測試涉及的參數更多，算法更為復雜，因此本文的最大迭代數Gmax設置為2500，經過測試可以確保每次迭代都收斂到某個結果。

5.3 測試結果與分析

本次仿真測試共安排了7個實驗組，各組的飛機數和停機位數如表10所示，實驗結果如表11所示。

表10 各實驗組的飛機數和停機位數

表11展示了所有7個仿真實驗組的測試結果，評價算法性能的指標是500，1000，2500代得分的平均值以及2500代得分的最高值。可見經典DE算法在1000代后尋優的能力下降，偶爾會出現經過2500次迭代后結果仍不收斂的情況，證明它在求解復雜優化問題時更容易搜索停滯，陷入局部最優解。相比之下，改進后的DE算法在各迭代節點上的得分普遍更高，在1500代甚至2000代后依然具有尋優能力。經過變異策略改進和參數自適應變化的DE算法搜索能力和收斂性能都有一定的提升，證明了算法改進的有效性。

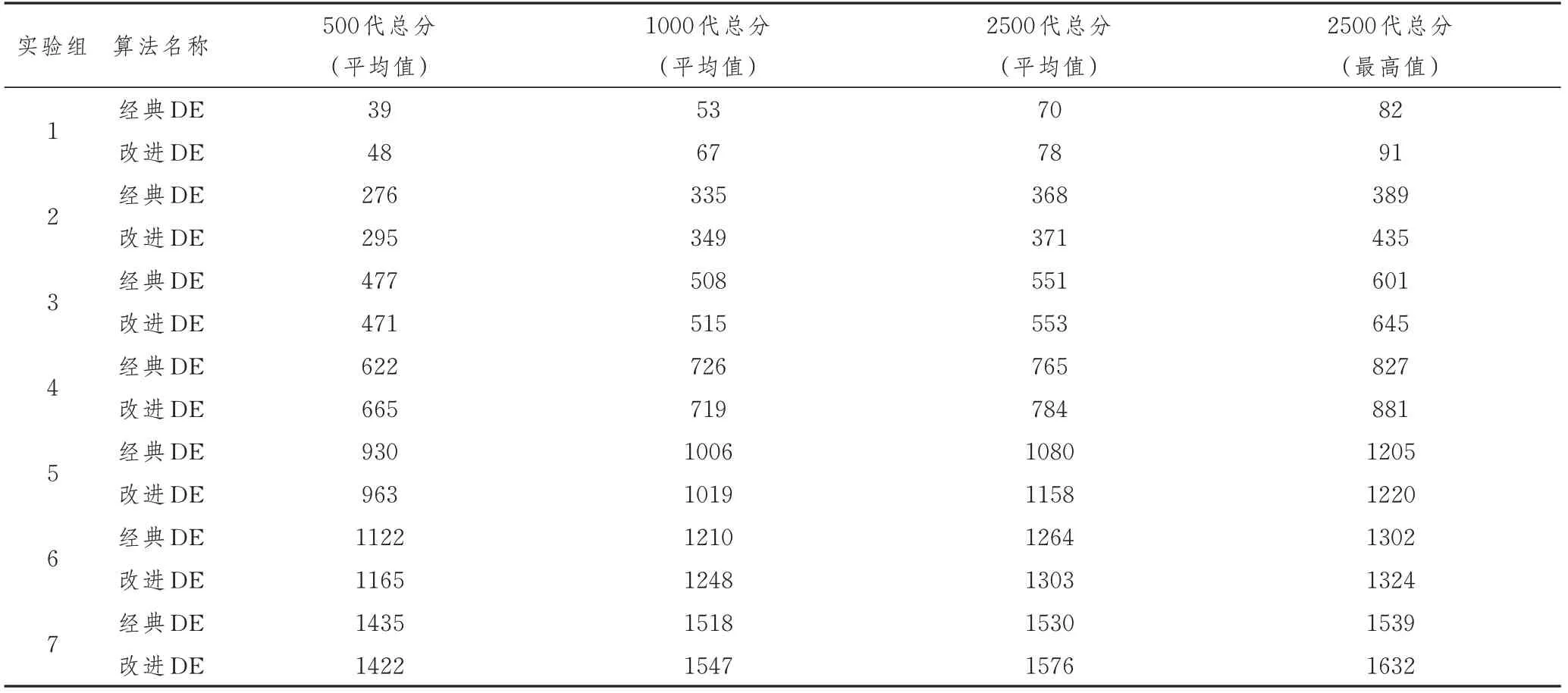
表11 停機位分配仿真測試結果

總之，通過對停機位分配這一實際問題的分析，可以發現改進后的DE算法在解本文建立的數學模型，進而解決停機位分配問題上具有明顯的優勢，可以更好地實現減少旅客轉移時間，提高機場運行效率等現實中的優化目標。

6 總結與展望

本文基于機場實際運行規則和停機位分配的有關約束條件，建立了基于航班-機位分值矩陣（FS）和航班-航班分值矩陣（FF）加權分值的多目標優化模型。將旅客最少步行距離或航班的最大靠橋率等通過分數加權矩陣的形式表示，再求出總得分的最大值。不再需要對現實中具體的優化目標進行計算，并且可以兼顧到單位不同，難以同時量化的多個優化目標。另外本文對經典DE算法的變異策略進行改進，增加了一個縮放因子K，同時讓K和CR隨迭代數的改變而自適應變化。實驗表明這樣在標準測試函數與停機位分配仿真測試中收斂更快，能夠搜索到比原算法更優的解，證實改進后算法的性能有所提升。后續工作可以嘗試采用機場的實際數據得到現實中的停機位分配方案，則本次研究將更具意義。最后，在機場的實際運行中，航班晚點的情況是比較常見的，此時之前制定的預分配的方案將不再適用。如何應對實際運行中的這類不確定因素，提高模型的魯棒性，實現實時的停機位分配，是一個未來值得繼續深究的方向。