例談不等式中的消元技巧
?浙江省寧波市鄞州中學 徐欣欣
1 引言
數學運算是高中數學學科核心素養之一,運算能力的缺乏已經嚴重掣肘學生數學學科核心素養的提升,筆者對數學運算中常用的技巧和思想加以總結,希望能助學生打破固有思路局限,拓展數學思維,并提升反思總結的能力.不等式問題中經常會碰到多變量問題,日常教學中,學生碰到不等式問題往往習慣性用不等式的性質去解.盡管部分多變量問題可以用不等式直接解決,但大多數時候若用消元處理則可以起到事半功倍的效果.本文中以不等式問題舉例說明代入消元、整體換元消元、等價轉化消元的運用.
2 消元法的應用技巧
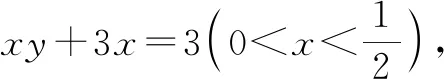
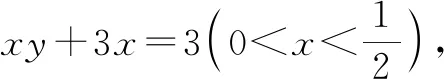
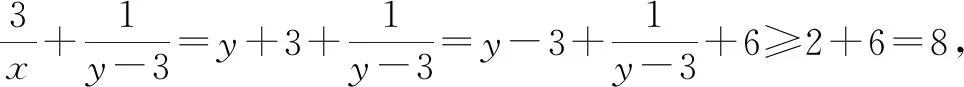
評注:該例題通過代入等式消元,轉化為單變量的函數問題,若求最值則需要驗證等號能否取到,若求范圍則需要把函數定義域求解準確.代入消元是最基本的消元方法,經常使用.
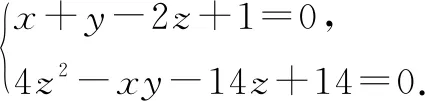
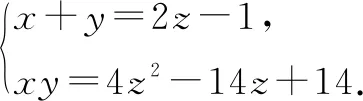
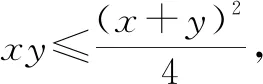
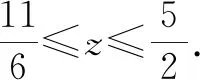
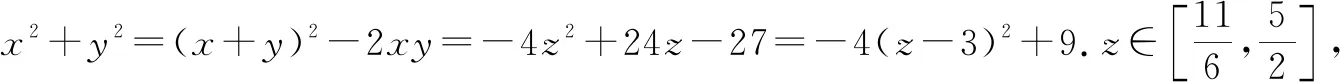
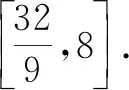
評注:該例題依舊是通過代入等式消元,轉化為單變量的函數問題,但有所變化.已知條件中有x,y,z三個變量,而問題中只有x,y兩個變量,常規想法是先消變量z,再消變量x或y,此題根據代數式特征直接消去了x,y變量,保留了z變量.
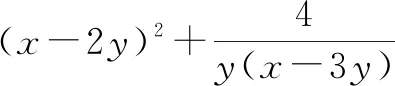
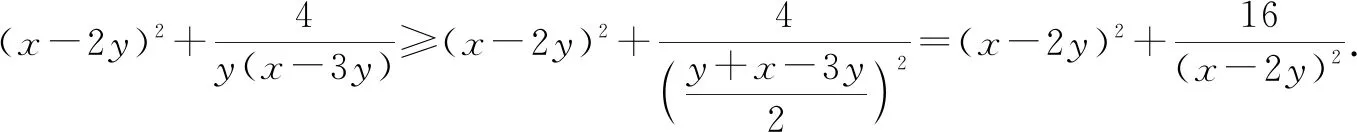
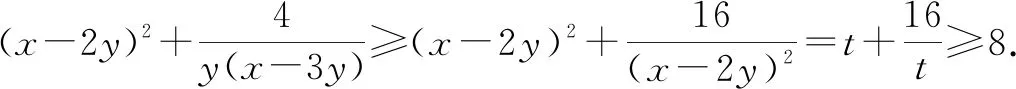
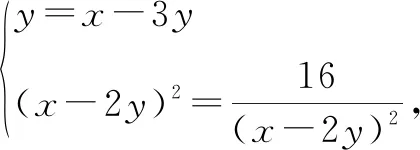
評注:該例題的關鍵是由y+(x-3y)=x-2y發現可以把x-2y看作一個整體,進行整體換元,從而達到消元目的.整體換元不僅可以把含兩個變量的式子看作一個整體,也可把含三個、四個變量的式子看作一個整體,從而同時消去多個變量.
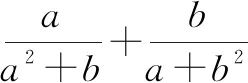
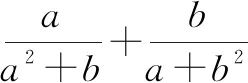
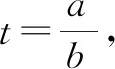
例5已知a>0,b>0,證明不等式:
證明因為a≠b,所以不妨設0 所以函數f(t)在區間(1,+∞)上單調遞增,所以f(t)>f(1)=0. 例6已知實數a,b,c滿足a2+2b2+3c2=1,則a+2b的最大值為. 解由a2+2b2+3c2=1,得a2+2b2≤1. 評注:該例題第一步通過等式轉化為不等式從而達到消元效果.此過程看似簡單,實則不易想到,關鍵是需要理解等價性,此題取到最值時存在滿足條件的c即可. 代入消元有代入等式消元和代入不等式消元,代入不等式消元有時需要對代數式進行主元處理.比值消元作為整體換元消元中一類最常用的消元方式,往往需要對代數式進行齊次化處理.消元不僅在不等式問題中經常使用,對于其他情形的多變量問題,照樣適用,而且對消元順序的處理,往往能提供解題思路,所以培養學生的消元意識,學會消元技巧至關重要.Z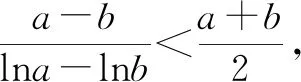
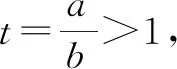
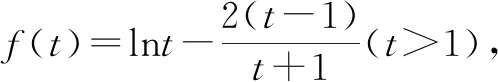
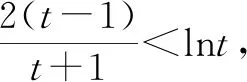
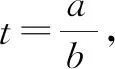

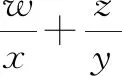
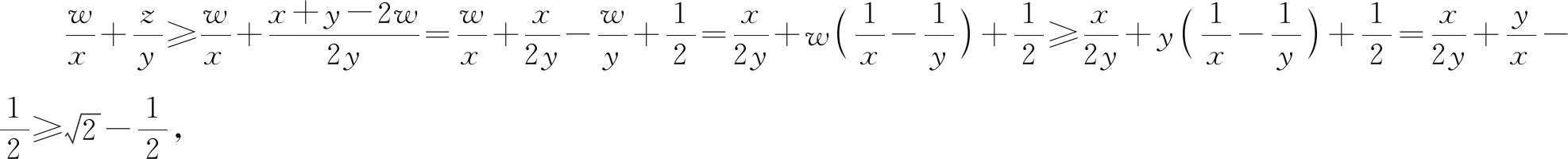
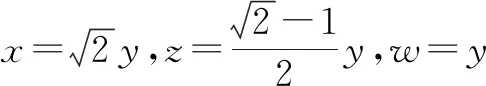
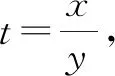
3 總結

