基于Markov切換的HIV傳染病模型的動態分析

董朝麗

（江西農業大學 南昌商學院，江西 共青城 332020）

0 引言

HIV病毒通過攻擊CD4T淋巴細胞，導致人類身體免疫功能喪失，感染各種疾病致死。從HIV病毒發現以來，每年約有上百萬人被感染HIV病毒，具有非常迅速的傳播能力［1-2］。因此，國內外十分重視HIV病毒，研發HIV病毒治療手段，降低艾滋病死亡率，時至今日，艾滋病治療已經取得些許療效，但是并未完全攻克艾滋病毒，依然是世界上未解傳染病［3］。基于此，國內外眾多學者紛紛采用多種手段，建立艾滋病病毒HIV模型，分析病毒模型特征，以期攻克艾滋病。

國內外眾多學者運用數學知識，從宏觀和微觀兩種角度著手，建立HIV傳染病的四維模型、常微分方程模型、離散數學模型、動力學模型、多種類型的傳染病模型等，分析HIV病毒的傳染過程、增殖現象、傳播時間、周期性等特征［4-5］。在國內外基礎上，相關學者針對HIV傳染病模型，作出如下研究。文獻［6］針對傳染病發病率和潛伏期等信息，建立SEIR傳染病模型，根據模型的平衡點，分析模型的動力學特征。文獻［7］根據傳染病的雙線性發生率和飽和治愈率等信息，建立SIR傳染病動力學模型，分析模型的穩定性。文獻［8］將Beverton-Holt函數與傳染病的雙時滯特點相結合，建立階段結構傳染病模型，分析模型的穩定性。文獻［9］根據傳染病周期，建立傳染病動力模型，分析傳染病生存周期。文獻［10］通過建立SEIR傳染病模型，分析傳染病的局部穩定性，并采用數值模擬的方式，驗證分析結果。文獻［11］通過Liapunov函數，建立SIQS傳染病模型，證明模型的滅絕性和持久性，并采用數值模擬的方式，驗證分析結論。文獻［12］根據傳染病的信息變量和治愈率信息，建立傳染病的一類SI傳染病模型，根據模型的平衡點，分析模型的穩定性。文獻［13］根據傳染病的非線性傳染率，建立傳染病模型，通過模型的時滯，分析模型Hopf分支和穩定性。在上述研究基礎上，此次研究采用Markov切換，進一步分析HIV傳染病模型的動態性，提出基于Markov切換的HIV傳染病模型的動態分析，以期為艾滋病攻克提供更多參考依據。

1 基于Markov切換的HIV傳染病模型的動態分析方法

1.1 建立HIV傳染病模型

HIV傳染病在人群中傳播，存在8～9年的潛伏期［14］。因此，將HIV傳染病，分為易感、潛伏、已經感染、免疫4種狀態，作為HIV傳染病模型節點，分別采用字母Y、Q、G、M表示。其中，易感Y表示非常容易感染HIV病毒的個體；潛伏Q表示已經感染HIV病毒，但個體并不知情，因此并未采取任何治療措施；已經感染G表示個體已經發現自己感染HIV病毒，并采取積極的治療隔離措施；免疫M表示不容易感染或已經治療好的HIV病毒個體，具有一定的抗病毒能力，且不再具有傳染性［15］。

基于此，存在具有n個節點的網絡O，則每個節點i∈{1 ,2,…,n}，在時間t時，具有Xi(t)∈{Y,Q,G,M}狀態。從上述描述中可以看出，若有一個節點Y被HIV病毒感染，至少會產生XQ(t)狀態和XG(t)狀態。為此，在節點的有向網絡中，將節點i鄰居分為感染鄰居和可能被感染的鄰居2類。此時，可以將HIV傳染病，按照動力學狀態轉移，分為2種傳播模式（圖1）。

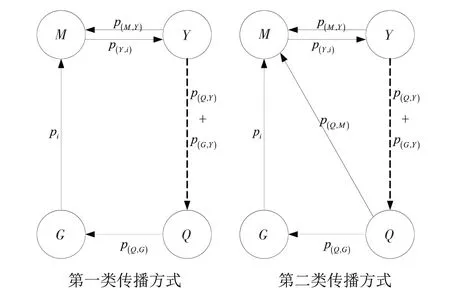
圖1 HIV傳染病2種傳播模式Fig.1 Two transmission modes of HIV infectious diseases

圖1中，pi表示能被網絡A中的節點j感染的節點i的恢復概率；p(Y,i)表示節點i恢復后，重新轉變為XY(t)的概率；p(Q,Y)表示Y被網絡中Q感染的概率；p(G,Y)表示Y被G感染的概率；p(M,Y)表示Y轉變為M的概率；p(Q,G)表示Q轉變為G的概率；p(Q,M)表示Q轉化為M的概率。其中，p(Q,Y)和p(G,Y)之間存在p(Q,Y)＜p(G,Y)、p(Q,Y)=p(G,Y)、p(Q,Y)＞p(G,Y)3種關系［16］。

此外，假設網絡O的鄰接網絡為A，當網絡O中的節點i能被網絡A中的節點j感染時，存在aij=1，即反之，aij=0。從上述分析中可以看出，網絡中的感染參數是非負的。為此建立的2類不同傳播方式的HIV傳染病模型如下：

綜合上述內容，即可完成HIV傳染病模型建立，此時，只需要尋找模型的參數，將模型參數與傳播方式相結合，以此來分析HIV傳染病模型的動態性質。

1.2 基于Markov切換計算HIV傳染病模型參數

從圖1中可以看出，此次建立HIV傳染病模型，設計pi、p(Y,i)、p(Q,Y)、p(G,Y)、p(M,Y)、p(Q,G)、p(Q,M)幾個概率值，結合式（1）和式（2），當幾個概率值達到最大化時，可以得到模型中HIV傳染病4種狀態傳播過程的最優傳播參數。基于此，采用Markov切換訓練的方式求取，其求取步驟如下：

⑥最終得到HIV傳染病模型，概率分布向量γ、狀態轉移矩陣P、觀測值矩陣B的最優值，其表達式如下：

綜合上述6步得到的HIV傳染病模型參數最優值，結合HIV傳染病模型，確定HIV傳染病模型的動態性質。

1.3 確定HIV傳染病模型的動態性質

如式（2）和式（3）所示的HIV傳染病模型，根據式（4）所示的模型3個參數最優值，計算HIV傳染病模型的平衡點，判斷模型的穩定性，得到穩定閾值，從而通過穩定閾值，確定HIV傳染病模型的動態性質。

依據圖1中HIV傳染病第一類傳播模式，以及式（1）所示的第一類HIV傳染病模型，設HIV傳染病模型的無病平衡點為Qi(t)=Gi(t)=0，將其記為?i(t)，則有：

綜合上述內容，只有滿足式（9）和式（10）所示的條件時，HIV傳染病模型的無病平衡點Qi(t)=Gi(t)=0才能實現，具有動態穩定性。

2 數值模擬

為驗證此次研究對HIV傳染病模型的動態穩定性分析結果，根據此次研究計算，設定pi、p(Y,i)、p(Q,Y)、p(G,Y)、p(M,Y)、p(Q,G)、p(Q,M)幾個概率值參數，進行數值模擬，并將模擬的數值代入上述10個公式的計算過程中，得到模型參數的最大特征值λmax，以此驗證此次研究計算結果。

2.1 數值設定

第一類傳播模式傳播模型幾個概率參數值，設定2種情況下的數值模擬，其具體數值設定如下：

（1）第一種情況：p(Y,i)=0.010，pi=10，p(Q,Y)=0.006，p(G,Y)=0.005，p(Q,G)=0.040，p(M,Y)=0.003，此時最大特征值λmax=0.244 9＜1。

（2）第二種情況：p(Y,i)=0.010，pi=10，p(Q,Y)=0.100，p(G,Y)=0.034，p(Q,G)=0.065，p(M,Y)=0.045，此時最大特征值λmax=2.004 5＞1。

第二類傳播模式傳播模型幾個概率參數值，設定2種情況下的數值模擬，其具體數值設定如下：

（1）第一種情況：p(Y,i)=0.010，pi=10，p(Q,Y)=0.100，p(G,Y)=0.010，p(Q,G)=0.020，p(M,Y)=0.030，p(Q,M)=0.003，此時最大特征值λmax=0.707 1＜1。

（2）第二種情況：p(Y,i)=0.010，pi=10，p(Q,Y)=0.100，p(G,Y)=0.100，p(Q,G)=0.200，p(M,Y)=0.003，p(Q,M)=0.003，此時最大特征值λmax=7.071 1＞1。

2.2 模擬結果

2.2.1 第一類傳播模式傳播模型

根據此次實驗，設定的2種情況下，第一類傳播模式傳播模型幾個概率參數值，得到的HIV傳染病模型Y、Q、G、M4種狀態關于時間的圖像見圖2。

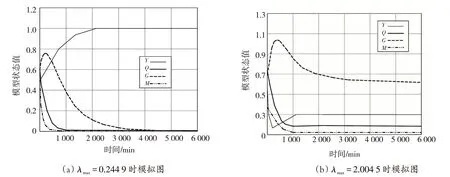
圖2 4種狀態關于時間的圖像Fig.2 Images of four states about time

從圖2中可以看出，第一類HIV傳染病模型的穩定性屬于全局漸進穩定。驗證了此次研究計算的模型動態穩定性。

2.2.2 第二類傳播模式傳播模型

根據此次實驗，設定的2種情況下，第二類傳播模式傳播模型幾個概率值參數值，得到的HIV傳染病模型Y、Q、G、M4種狀態關于時間的圖像見圖3。

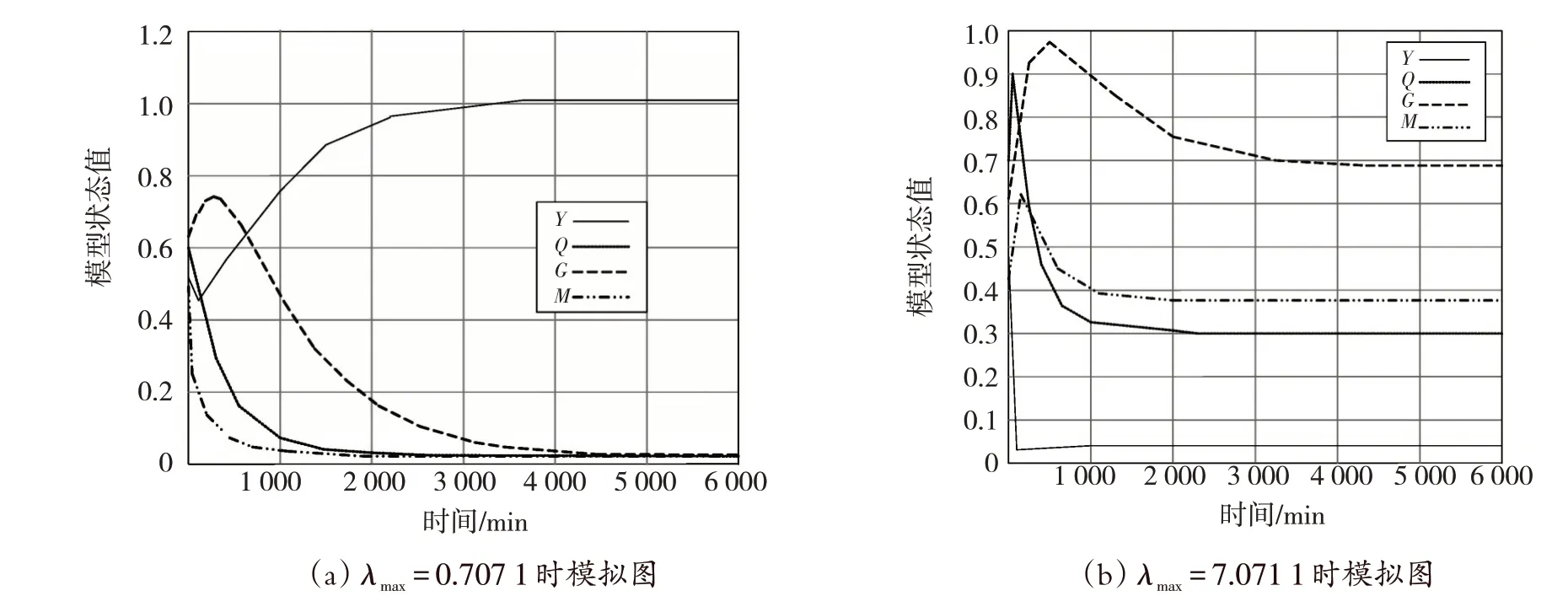
圖3 4種狀態關于時間的圖像Fig.3 Images of four states about time

從圖3中可以看出，第二類HIV傳染病模型的穩定性，同樣屬于全局漸進穩定。驗證了此次研究計算的模型動態穩定性。

3 結束語

此次研究，利用Markov切換，計算模型最優特征值，以此獲取模型最大特征值，確定模型動態穩定性。并采用模擬數值的方式，驗證此次分析結果的正確性。但是，此次研究分析HIV傳染病模型的動態穩定性，研究方向較為單一，在今后的研究中，還需深入研究HIV傳染病模型的復雜性、滅絕性和動態性，從而為HIV傳染病治療提供依據。