用導數研究不等式問題的解題策略

■江蘇省泰興市第二高級中學 陳貴東

本文探究用導數研究不等式恒成立、構造函數證明不等式等問題的解題策略,希望對同學們的復習備考能有所幫助。

策略1:含參不等式恒成立問題中的“分離參數構造函數法”

例1(2022屆重慶市高三上學期第二次質量檢測)已知函數f(x)=-(m+1)x+mlnx+m,f＇(x)為函數f(x)的導函數。

(1)討論f(x)的單調區間;

(2)若xf＇(x)-f(x)≥0恒成立,求m的取值范圍。

解析:(1)由題意知,函數f(x)的定義域為(0,+∞),f＇(x)=x-(m+1)+。

若m≤0,當x∈(0,1)時,f＇(x)＜0,f(x)單調遞減;當x∈(1,+∞)時,f＇(x)＞0,f(x)單調遞增。

若0＜m＜1,當x∈(0,m)時,f＇(x)＞0,f(x)單調遞增;當x∈(m,1)時,f＇(x)＜0,f(x)單調遞減;當x∈(1,+∞)時,f＇(x)＞0,f(x)單調遞增。

若m=1,當x∈(0,+∞)時,f＇(x)≥0,f(x)單調遞增。

若m＞1,當x∈(0,1)時,f＇(x)＞0,f(x)單調遞增;當x∈(1,m)時,f＇(x)＜0,f(x)單調遞減;當x∈(m,+∞)時,f＇(x)＞0,f(x)單調遞增。

(2)因為xf＇(x)-f(x)≥0恒成立,即-mlnx≥0,所以≥mlnx對任意的x∈(0,+∞)恒成立。

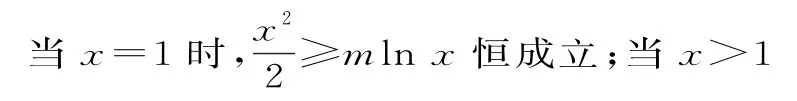
綜上所述,0≤m≤e,即m的取值范圍為[0,e]。

感悟:若不等式恒成立問題中的參數可分離,則可采用分離參數構造函數法進行求解。即f(x,λ)≥0(x∈D)(λ是實參數)恒成立,將f(x,λ)≥0轉化為λ≥g(x)或λ≤g(x)(x∈D)恒成立,進而轉化為λ≥g(x)max或λ≤g(x)min(x∈D),用導數法求g(x)的最值,對于復雜問題分離參數時需要分類討論。

策略2:依據不等式的結構特征構建新函數求解恒成立問題

例2(2022 屆皖豫名校聯盟體高三上學期第一次聯考)已知函數f(x)=2x+-1的圖像與直線y=1相切。

(1)求實數a的值;

(2)若k＜2,且f(x)≥kx-1 恒成立,求實數k的最小值。

解析:(1)f＇(x)=2-。

若a≤0,則f＇(x)＞0,所以f(x)的圖像不存在斜率為0的切線。

若a＞0,令f＇(x)=0,可得x=,由題意+2-1=1,得a=2。

(2)設g(x)=f(x)-kx+1,則g＇(x)=2-k-。

因為k＜2,所以令g＇(x0)=0,可得k=2-,易知g＇(x)單調遞增。

所以在(-∞,x0)上,g＇(x)＜0,g(x)單調遞減;在(x0,+∞)上,g＇(x)＞0,g(x)單調遞增。

所以g(x)min=g(x0)=(2-k)x0+。

根據題意知g(x)≥0 恒成立,所以g(x)min=≥0,解得x0≥-1。

上賽季高速男籃打入半決賽，吊足了球迷的胃口，而新賽季面臨人才流失的局面，西王男籃新任主帥吳慶龍，提出了“保八爭六”的目標。然而，球隊接連碰到困難，兩個外援先后受傷，山東隊一度以全華班出戰，遭遇了七連敗，排名跌出前十。匆匆接手的西王男籃，顯然還沒有摸到俱樂部運營的門道。

當x0≥-1時,k=2-≥2-2e,即k的最小值為2-2e。

感悟:對于函數不等式恒成立或者有解求參的問題,常用變量分離或參變分離轉化為求新函數的最值問題;當參數不易分離時,把握不等式的特征作差構建新函數,再求新函數的最值,使得新函數的最值大于或者小于0 探究出參數的范圍;或者分離成兩個函數,使得一個函數恒大于或小于另一個函數的條件構建不等式求解。

策略3:把證明f(x)＞g(x)轉化為證明f(x)min＞g(x)max

例3(2022 屆重慶市南開中學高三上學期月考)已知函數f(x)=,g(x)=lnx。

(1)當a＞0時,討論函數F(x)=af(x)-g(x)-的單調性;

(2)當a＞1 時,求證:axf(x)-g(ax)＞(e-1)x+1。

解析:(1)F(x)=的定義域為(0,+∞),F＇(x)=,令F＇(x)=0,得x=1或x=-lna。

①若-lna＞1,即a∈,則當x∈(0,1)時,F＇(x)＞0;當x∈(1,-lna)時,F＇(x)＜0;當x∈(-lna,+∞)時,F＇(x)＞0。所以F(x)在(0,1)上單調遞增,在(1,-lna)上單調遞減,在(-lna,+∞)上單調遞增。

②若-lna=1,即a=,則當x∈(0,+∞)時,F＇(x)＞0,所以F(x)在(0,+∞)上單調遞增。

③若0＜-lna＜1,即a∈,則當x∈(0,-lna)時,F＇(x)＞0;當x∈(-lna,1)時,F＇(x)＜0;當x∈(1,+∞)時,F＇(x)＞0。所以F(x)在(0,-lna)上單調遞增,在(-lna,1)上單調遞減,在(1,+∞)上單調遞增。

(2)原式等價于F(x)≥-lnx+e-1。

因為a＞1,所以F(x)≥F(1)=ae-1,所以只需證-lnx+e-1≤ae-1,即證G(x)=-lnx≤(a-1)e。

求導得G＇(x)=,記h(x)=1-x-ln(ax),則h＇(x)=-1-＜0,所以h(x)在(0,+∞)上單調遞減。

所以G(x)≤G(x0)=-lnx0=-lnx0-1。

記φ(x)=-lnx-1,則φ(x)在上單調遞減,所以φ(x)＜=a+lna-1,故只需證a+lna-1＜(a-1)·e,即m(a)=(e-1)a-lna+1＞0。

因為m＇(a)=e-1-＞0,所以m(a)在(1,+∞)上單調遞增,所以m(a)＞m(1)=0成立,所以原不等式成立。

感悟:有時候把證明f(x)＞g(x)轉化為證明f(x)-g(x)＞0 后,可能會出現f(x)-g(x)的導函數很復雜,很難根據導函數研究f(x)-g(x)的最值,而f(x)的最小值及g(x)的最大值都比較容易求,可考慮利用證明f(x)min＞g(x)max的方法證明原不等式,但要注意這種方法有局限性,因為f(x)＞g(x)未必有f(x)min＞g(x)max。

策略4:多變量不等式通過換元法減元構造新函數求值域證明不等式

例4(2022 屆廣東省廣州市省四校2022屆高三上學期聯考)已知函數f(x)=-2ax+lnx。

(1)若f(x)為增函數,求實數a的取值范圍。

(2)設g(x)=xf(x)-+2x有兩個不同的零點x1,x2。

①證明:x1+x2＞;

②若x2-3x1≥0,證明:x1+x2＞。

解析:(1)由題意知,函數f(x)的定義域為(0,+∞)。

由于f(x)為增函數,則f＇(x)=x+-2a≥-2a=2-2a≥0 恒成立,故a≤1。

(2)①g(x)=x(lnx+2-2ax),由g(x)=xf(x)-+2x有兩個不同的零點x1,x2,得方程lnx+2-2ax=0(x＞0)有兩個不同的根為x1,x2,不妨設x2＞x1＞0,則兩式相減得lnx2-lnx1=2a(x2-x1),所以a=。

感悟:對于多變量不等式問題,其一般的處理策略為消元或是把一個看作變量再探究其他常量或所選變量之間的關系,通過變形換元產生一個新變量的函數,進而用導數確定新變量函數的值域,從而順利求解。