密閉空間內六硝基六氮雜異伍茲烷基復合炸藥能量釋放特性

劉正,聶建新,徐星,朱英中,劉攀,郭學永,閆石,張韜

(1.北京理工大學 爆炸科學與技術國家重點實驗室,北京 100081;2.內蒙航天動力機械測試所,內蒙古呼和浩特 010076;3.重慶紅宇精密工業集團有限公司,重慶 402760)

0 引言

現代戰爭中越來越多的重要軍事目標位于地下密閉空間,含鋁炸藥因為其具有高爆熱和高做功能力等特點而被廣泛用作打擊此類目標。密閉空間爆炸不僅存在沖擊波,還存在熱效應和準靜態壓力等諸多毀傷元素。準靜態壓力表征了總能量的集聚,是破壞目標的一個重要毀傷元素。美國海軍水面武器中心在比較密閉空間中的炸藥威力時采用準靜態壓力作為唯一的威力評估參數。

Anderson等總結分析了大量密閉爆炸實驗數據,結合無量綱分析方法得出了影響準靜態壓力、持續時間和沖量的因素。Weibull通過梯恩梯(TNT)半密閉爆炸實驗證明準靜態壓力和通風孔無關,而與炸藥與容器體積的比值有關(kg/m)。Trzciński等研究了黑索今(RDX)基含鋁炸藥在0.15 m和7.00 m爆炸容器中的準靜態壓力,發現含鋁炸藥的準靜態壓力均大于純RDX炸藥的準靜態壓力,表明鋁粉與爆轟產物和空氣中的氧發生了反應,并通過氟化鋰代替鋁進行了驗證。Feldgun等通過理論分析提出了用于預測準靜態壓力的模型,研究了熱容比和爆炸能量對準靜態壓力的影響,發現熱容比對準靜態壓力的影響要大于爆炸能量。Edri等和Feldgun等通過TNT半密閉爆炸實驗研究了其密閉爆炸特性,并結合理論分析和數值模擬分析了爆炸產物后燃對結果的影響。國內學者對此也進行了大量研究。王等旺等、張玉磊等和劉文祥等先后通過理論和實驗研究分析了TNT的密閉爆炸特性,并擬合出了適用于一定范圍內的準靜態壓力計算公式。徐維錚等基于化學反應分析和能量守恒定律提出了考慮后燃燒效應的準靜態壓力理論計算模型,并且驗證了模型的可靠性和正確性。Duan等對鋁氧比從0.25～1.23的RDX基含鋁炸藥進行了密閉爆炸實驗,發現隨著鋁氧比的增加,準靜態壓力先升高后降低,在鋁氧比為0.99時準靜態壓力達到最大。 同年,楊雄等研究了鋁氧比分別為0.254、0.361、0.483和0.623的奧克托今(HMX)基含鋁炸藥真空條件下密閉空間爆炸準靜態壓力,發現在鋁氧比為0.361時準靜態壓力最大。Fan等通過研究RDX基含鋁炸藥在密閉空間中的爆炸,發現空氣環境下爆炸的準靜態壓力高于真空環境,粒度級配有助于提高初始階段鋁粉的反應率。Fan等在改進JWL狀態方程的基礎上,提出了考慮后燃效應的含鋁炸藥準靜態壓力計算模型。Wang等研究了相鄰腔室爆炸的壓力載荷特性,發現相鄰腔室的存在不會影響主腔室理論計算的準靜態壓力。

國內外已經開展了大量RDX和HMX基含鋁炸藥密閉爆炸特性研究,但是對六硝基六氮雜異伍茲烷(CL-20)基復合炸藥密閉空間爆炸準靜態壓力影響因素研究較少,且影響因素研究多為鋁氧比和粒徑等,化學組成結構參數藥氧比作為影響復合炸藥爆炸能量釋放的重要影響因素之一,同樣研究較少。因此本文通過實驗研究、理論計算和數值仿真,研究密閉空間內不同藥氧比對CL-20基復合炸藥能量釋放特性的影響,以期為先進溫壓戰斗部用高能炸藥配方設計與優化提供參考。

1 密閉空間CL-20基復合炸藥爆炸實驗

1.1 密閉爆炸裝置及測試儀器

實驗采用500 L密閉爆炸容器,上部為球型,下部為圓柱型,尺寸為900×800 mm,如圖1所示。傳感器采用瑞士伯爾尼Kistler儀器公司生產的603-BQ-01型壁面壓力傳感器,傳感器的靈敏度為0.5 V/MPa,布置在外接傳壓管處,傳壓管距圓柱底端400 mm處。用成都南匯科技有限公司生產的VXI高速數據采集器記錄數據,采樣速率為200 kHz/s。

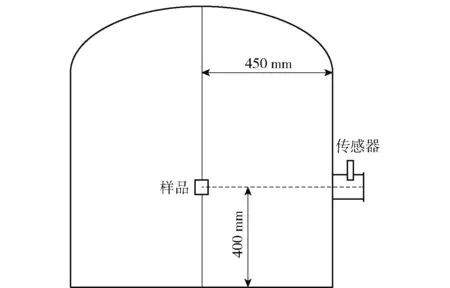
圖1 爆炸裝置示意圖Fig.1 Schematic diagram of explosive chamber

1.2 實驗樣品設計

復合炸藥一般由高能單質炸藥、氧化劑、可燃劑和粘結劑等組成。鋁氧比和藥氧比是設計炸藥樣品配比的關鍵參數,鋁氧比為單位質量復合炸藥中鋁元素與氧元素物質的量之比,藥氧比為單位質量復合炸藥中單質炸藥氧元素與復合炸藥氧元素物質的量之比。和的定義式分別如下:

式中:為單位質量復合炸藥中鋁元素物質的量;為單位質量復合炸藥中O元素物質的量。

式中:為單位質量復合炸藥中單質炸藥氧元素物質的量(mol/kg)。

不同藥氧比CL-20基復合炸藥實驗樣品采用CL-20/鋁/高氯酸銨(AP)/氟橡膠四元壓裝體系,依據控制變量法,固定鋁氧比為0.6,制備5組不同藥氧比樣品藥柱。藥柱密度為理論密度的96%,長徑比為1∶1,藥柱總質量為100 g。為了起爆可靠性,采用20 g JH14炸藥作為起爆藥。根據熱容法計算復合炸藥爆炸鋁粉初始燃燒溫度,不同藥氧比實驗樣品參數如表1所示。圖2所示為不同藥氧比樣品實物圖。

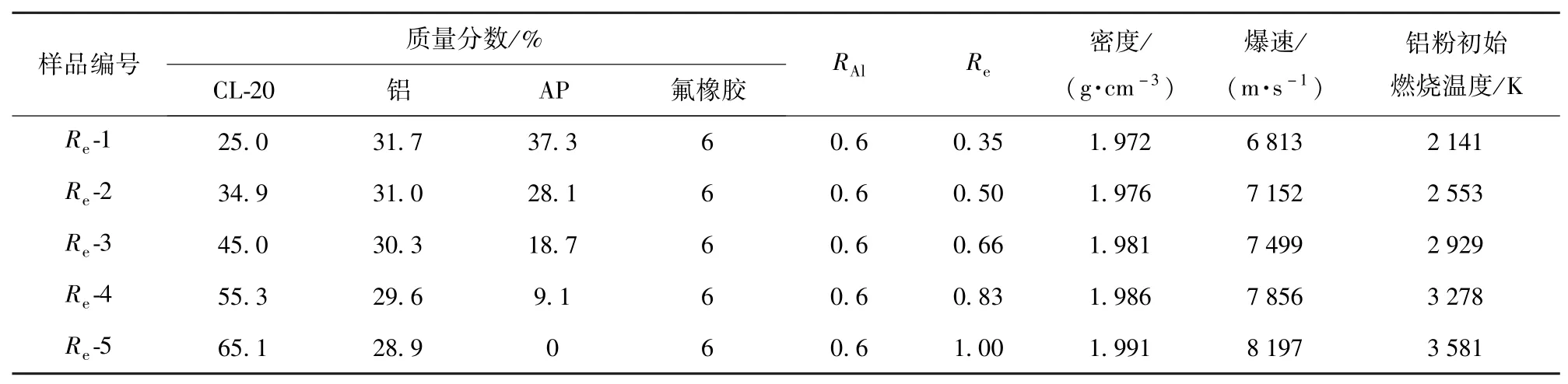
表1 樣品組成和參數Tab.1 Compositions and parameters of explosive samples

圖2 不同藥氧比樣品實物圖Fig.2 Physical picture of explosive samples with different R e

1.3 準靜態壓力測試結果

目前計算準靜態壓力的方法國內外學者各有不同,主要有兩種方法:一種方法是采用相鄰平均法對壓力-時間曲線進行平滑處理,定義處理后的壓力峰值為準靜態壓力;另一種方法是取沖擊波后一定時間段內的平均壓力作為準靜態壓力。由于準靜態壓力是沖擊波在密閉空間內多次反射后形成的壓力,其幅值比反射沖擊波峰值小很多,但作用時間較長。顯然,第1種方法直接取平滑后曲線的峰值壓力作為準靜態壓力與實際情況不符,且誤差較大;第2種方法在實際運用中實驗結果的重復性好,可更大程度地減小測試誤差。因此,本文選擇5～20 ms內壓力的平均值作為炸藥密閉空間內爆炸的準靜態壓力。不同藥氧比炸藥樣品的準靜態壓力實驗結果如圖3所示。

由圖3可知,隨著藥氧比的增加,CL-20基復合炸藥準靜態壓力先升高后降低,在藥氧比為0.83時達到最大值。這是因為隨著藥氧比的增加,即主體炸藥含量增加,使得鋁粉燃燒的初始溫度升高,提高了鋁粉的燃燒速率,使得鋁粉燃燒更加充分,準靜態壓力提高。當藥氧比超過0.83時,雖然鋁粉燃燒速率較高,但氧化劑含量急劇減少加之有限空間內爆過程的空間體積有限,使得鋁粉的燃燒受到影響,鋁粉燃燒釋放的能量降低,導致準靜態壓力降低。

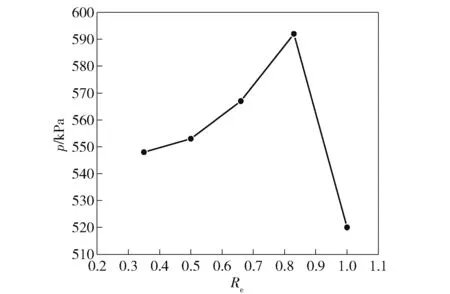
圖3 不同藥氧比樣品準靜態壓力Fig.3 Quasi-static pressures of explosive samples with different R e

根據理想氣體絕熱模型,準靜態壓力分為兩部分,即爆轟產生的氣體在密閉空間擴散形成的壓力和爆炸釋放的能量使密閉空間內溫度升高而導致的壓力。準靜態壓力可表示為

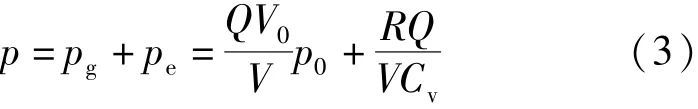
式中:為爆炸釋放的能量;為爆容;為密閉容器初始壓力;為密閉空間體積;為氣體常數;為氣體定容比熱。

根據EXPLO5程序計算可知,不同藥氧比樣品的爆容最大為332.42 L/kg,100 g樣品爆炸產生的氣體體積遠遠小于密閉爆炸容器體積500 L,在本文實驗中炸藥樣品爆炸反應的產氣量對準靜態壓力的貢獻可忽略不計。因此,炸藥爆炸釋放能量導致密閉空間內體系溫度升高,是影響準靜態壓力變化的主要因素。

為了進一步解釋圖3所示準靜態壓力隨藥氧比變化規律的本質機理,需要對復合炸藥爆炸過程中能量釋放特性進行深入分析。

2 復合炸藥爆炸能量釋放特性分析

2.1 復合炸藥理論儲能結構

通過(3)式可知,對準靜態壓力的貢獻主要是炸藥爆炸釋放能量使密閉空間內溫度升高而導致的壓力,而復合炸藥爆炸釋放的能量與理論儲能的高低直接相關。復合炸藥理論儲能是指復合炸藥爆炸在理論上的最大潛能,可表示為

式中:為分子內儲能,表示單質炸藥爆轟與氧化劑分解產生的能量;為分子間儲能,表示鋁粉爆轟波后燃燒釋放的能量。根據EXPLO5程序,分別計算了不同藥氧比復合炸藥的儲能、分子內儲能和分子間儲能,如表2所示。圖4所示為分子間儲能及其占比隨藥氧比的變化。

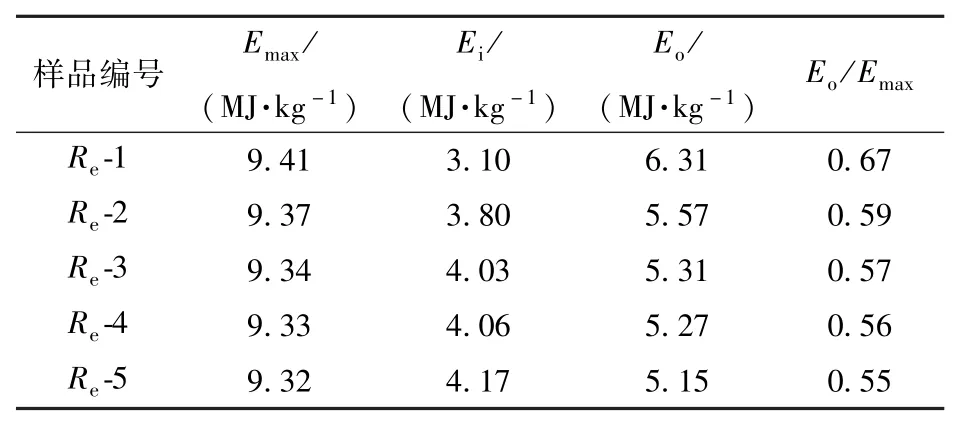
表2 不同藥氧比樣品儲能計算Tab.2 Calculation of energy storage of explosive samples with different R e

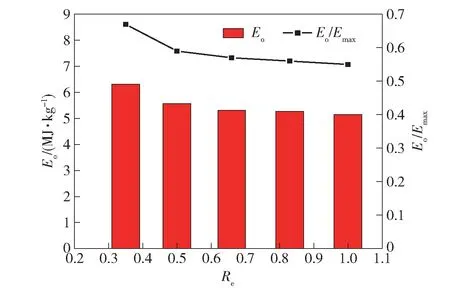
圖4 分子間儲能及其占比隨藥氧比的變化Fig.4 Variation of intermolecular energy storage and its percentage with R e

根據表2和圖4可知,隨著藥氧比增大,儲能基本不變,即藥氧比不會大幅改變儲能。分子間儲能及其在儲能中的占比呈現略微降低的趨勢,但最低占比也達到了55,因此分子間儲能是復合炸藥儲能的主體,分子間能量的釋放即鋁粉爆轟波后燃燒是復合炸藥能量釋放的關鍵。

2.2 鋁粉燃燒特性

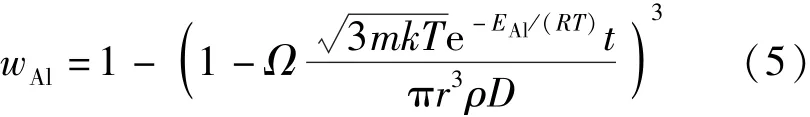
式中:為產物擴散系數;為每個鋁原子的質量;為波爾茲曼常數;為炸藥密閉空間爆炸溫度;為鋁的氣化焓;為原子半徑;為球狀鋁顆粒的密度;為鋁顆粒的直徑;為鋁顆粒的氣化時間。

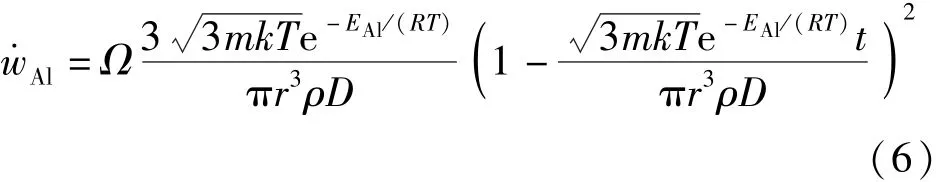
鋁粉在爆轟波后燃燒伴隨著爆轟產物的膨脹過程,體系溫度也隨之不斷變化,鋁的熔點為933 K,當體系溫度不足以支撐鋁粉燃燒時,后燃反應停止。大量實驗研究表明,炸藥密閉空間爆炸溫度時程曲線呈指數下降趨勢,可表示為

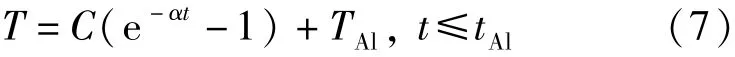
式中:和為常數,與炸藥特性和密閉空間有關,可由瞬態響應熱電偶測溫數據標定,本文中取2 750,取0.025;取值見表1;為密閉空間體系溫度降至鋁熔點的時間。

綜合應用(5)式、(6)式和(7)式,結合表1中復合炸藥爆炸參數,通過MATLAB軟件編程計算復合炸藥樣品中鋁粉燃燒度、燃燒速率和燃燒時間,結果如圖5和圖6所示。計算結果表明,=0.35時,鋁粉燃燒度=0.28,燃燒時間為24 ms,這是因為在小藥氧比條件下,爆轟環境提供給鋁粉燃燒的體系初溫較低,且爆轟產物與鋁粒子間相對運動速度較小即擴散系數小,進而導致鋁粉燃燒速率低,鋁粉燃燒不完全釋能不充分。隨著藥氧比的增加,鋁粉燃燒速率增大,鋁粉燃燒更完全釋能更充分。

圖5 不同藥氧比樣品鋁粒子燃燒度Fig.5 Combustion degree of aluminum particles of explosive samples with different R e

圖6 不同藥氧比樣品鋁粒子燃燒速率Fig.6 Combustion rate of aluminum particles of explosive samples with different R e

2.3 復合炸藥爆炸能量釋放規律

由于單質炸藥和氧化劑反應的時間尺度遠小于鋁粉爆轟波后燃燒的時間尺度,故假設單質炸藥和氧化劑在爆轟區內完全反應,分子內儲能完全釋放。因此炸藥爆炸后時間內釋放的能量可由(8)式計算:

式中:()表示時刻炸藥爆炸釋放的能量;()表示鋁粒子在時刻的燃燒度。

由于準靜態壓力取值為5～20 ms內的平均值,根據不同藥氧比樣品鋁粉燃燒度和儲能可計算=20 ms內復合炸藥爆炸釋放的能量,計算結果如表3所示。圖7所示為不同藥氧比樣品20 ms內釋放的能量。

表3 不同藥氧比樣品爆炸釋放的能量Tab.3 Calculation of energy storage of explosive samples with different R e

圖7 不同藥氧比樣品20 ms內釋放的能量Fig.7 Energy released from explosive samples with different R e in 20 ms

圖7表明,隨著藥氧比的提高,復合炸藥在0～20 ms內釋放的能量先升高后降低,藥氧比為0.83時,釋放的能量最多,與準靜態壓力隨藥氧比的變化趨勢相同。這是因為藥氧比的增加提高了鋁粉初始燃燒溫度,增大了擴散系數,鋁粉燃燒速率提高,爆炸釋放的能量提高,使得準靜態壓力增加。當藥氧比大于0.83時,盡管其鋁粉燃燒度較高,但由于分子間儲能占比更低,因而釋放的能量降低,準靜態壓力降低。而根據圖6可知,當藥氧比為1時,鋁粉燃燒速率在5 ms之后幾乎為0 m/s,即其能量在5 ms之前已基本釋放完全,5 ms之后無后續能量支撐準靜態壓力,導致相比較釋放的能量,準靜態壓力的降低更為明顯。

3 復合炸藥密閉空間爆炸數值模擬

為了進一步研究復合炸藥密閉空間爆炸能量釋放特性,利用有限元軟件AUTODYN對炸藥樣品在密閉爆炸容器中的爆炸過程進行數值模擬,研究密閉爆炸容器的形狀和體積對復合炸藥密閉空間爆炸準靜態壓力的影響規律。

3.1 不同測點準靜態壓力結果分析

參考密閉爆炸容器,建立如圖8(a)所示的模型,不帶傳壓管的模型如圖8(b)所示。圖8中空氣和炸藥均采用歐拉網格,密閉爆炸容器邊界均采用剛性邊界,不考慮壁面厚度及其變形,網格尺寸均為2 mm×2 mm,復合炸藥以填充的方式填入空氣域。分別在傳壓管內和傳壓管處壁面上設置2個監測點。

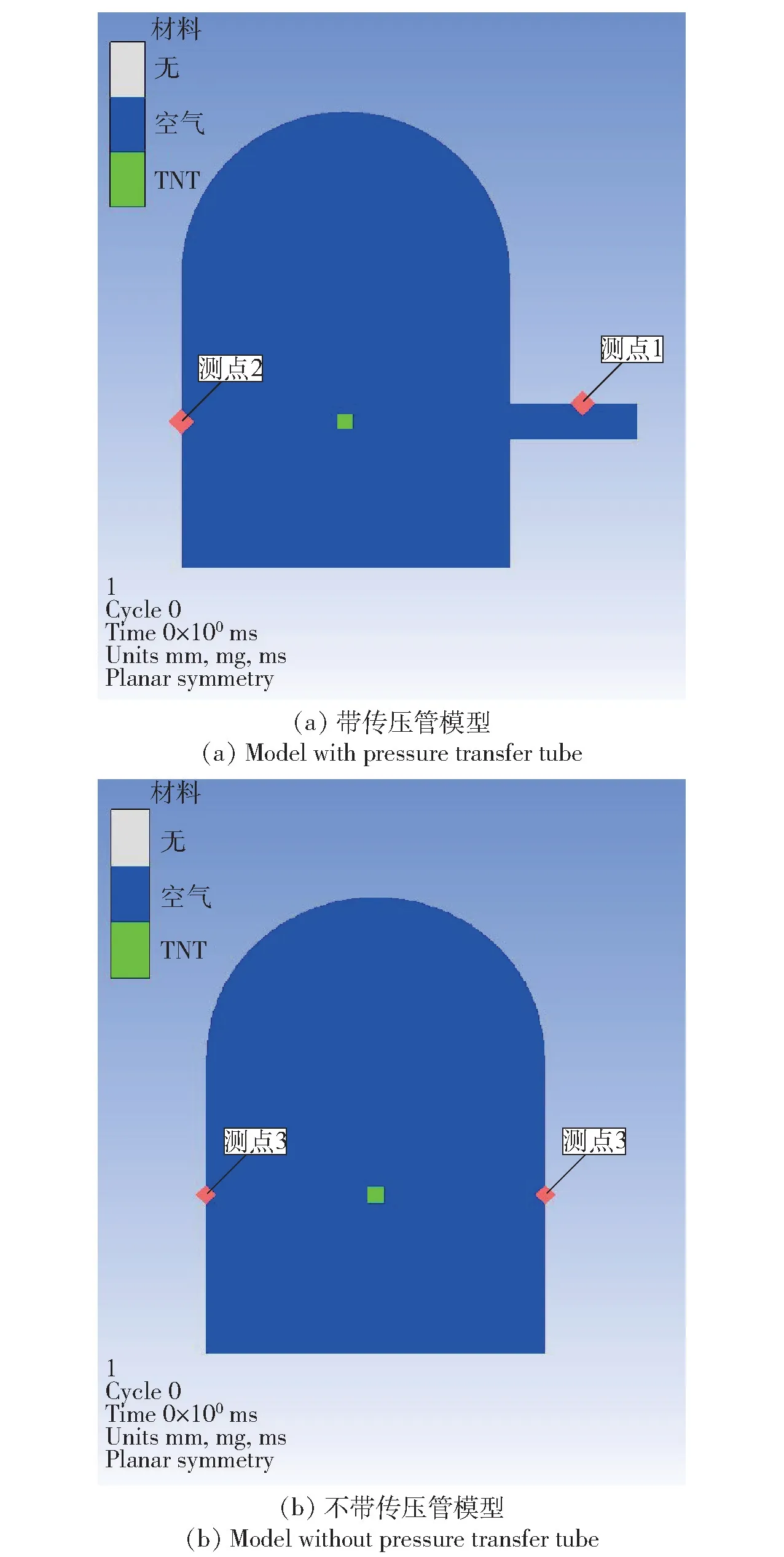
圖8 密閉爆炸容器模型及壓力測試點Fig.8 Explosive vessel model and pressure test points

采用JWL狀態方程來描述炸藥爆炸能量釋放過程,其表達式如下,

式中:為爆轟產物壓力;為產物相對比容;為產物的內能;、、、、均為狀態方程參數。TNT和空氣域均采用軟件自帶的狀態方程參數,具體參數如表4和表5所示。

表4 TNT的JWL狀態方程參數Tab.4 JWL equation of state parameters for TNT

表5 空氣狀態方程參數Tab.5 Air equation of state parameters

相同質量的TNT爆炸后,監測點1和監測點2處的壓力時程曲線如圖9所示。經計算可知5～20 ms內,監測點1和監測點2處的準靜態壓力分別為379 kPa和384 kPa,誤差為1.3%,因此可認為對于全密閉爆炸容器,傳壓管處壁面上測點的準靜態壓力等同于傳壓管內測點的準靜態壓力值。因此,本文為簡化計算,后續密閉空間內炸藥爆炸作用過程仿真分析采用無傳壓管結構模型計算。

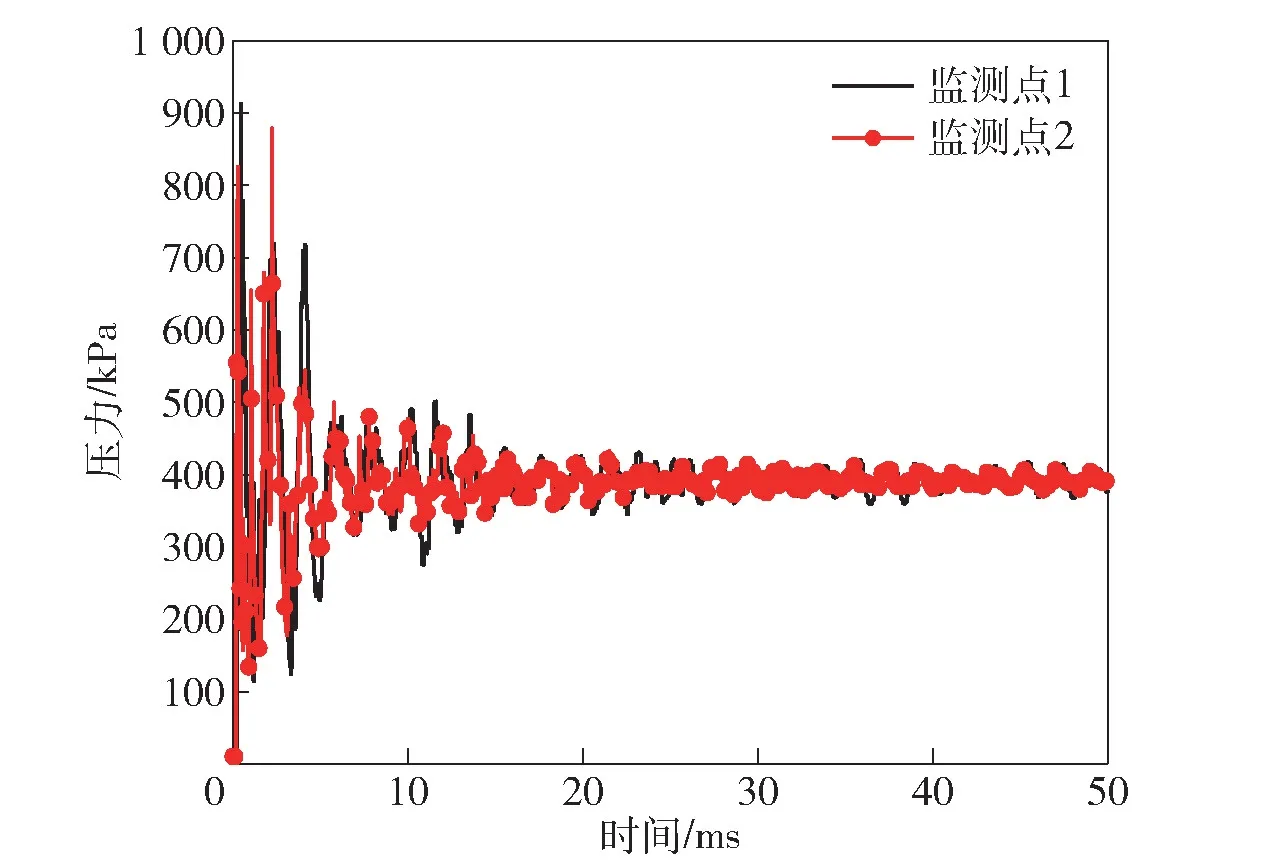
圖9 監測點1和監測點2處的壓力時程曲線Fig.9 Pressure-time curves at monitoring points 1 and 2

3.2 不同藥氧比準靜態壓力結果分析

采用無傳壓管結構模型,計算了不同藥氧比復合炸藥密閉空間爆炸的準靜態壓力。其JWL狀態方程參數為EXPLO5程序計算所得,具體如表6所示。

表6 不同藥氧比樣品JWL狀態方程參數Tab.6 JWL equation of state parameters for explosive samples with different R e

復合炸藥密閉空間爆炸過程的壓力云圖如圖10所示。由圖10可知,復合炸藥爆炸后,沖擊波向四周傳播,當接觸壁面后開始向內反射,隨著爆炸過程的繼續進行,壁面反射與地面反射相遇,并在爆炸容器角落產生較大壓力。如此反復,最終在密閉爆炸容器中形成一個平衡壓力。

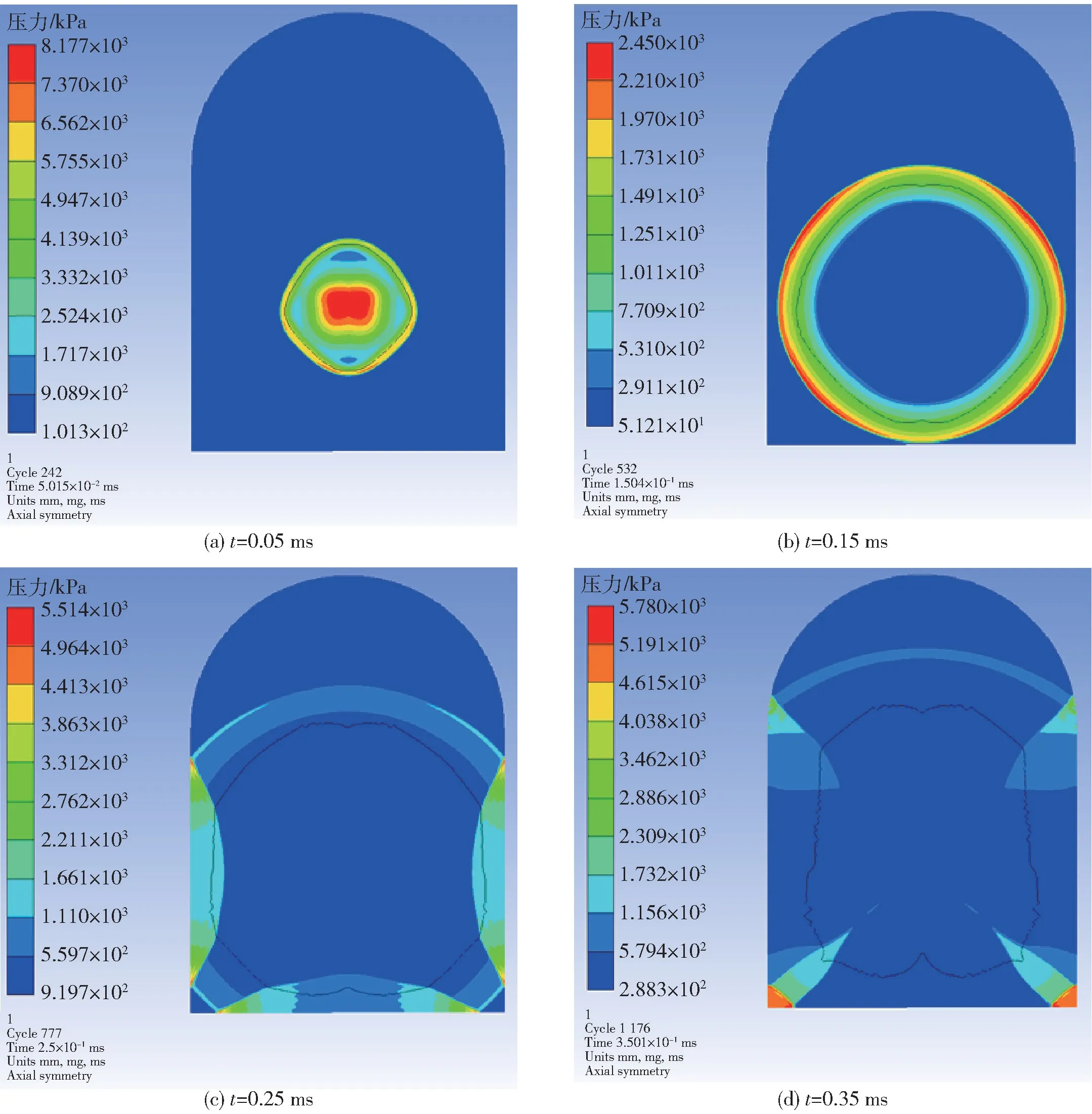
圖10 復合炸藥密閉空間爆炸壓力云圖Fig.10 Pressure nephograms of explosion of composite explosives in confined space

不同藥氧比樣品的準靜態壓力實驗結果和數值模擬結果如表7所示。由表7可知,不同藥氧比樣品準靜態壓力實驗結果與數值計算結果最大偏差為4.7%,在可接受范圍之內,表明本文建立的模型對密閉空間爆炸準靜態壓力的預測是可行的。

表7 不同藥氧比樣品準靜態壓力實驗與數值模擬結果Tab.7 Experimental and numerically simulated results of quasi-static pressure of explosive samples with different R e

圖11所示為不同藥氧比準靜態壓力變化。由圖11可知,準靜態壓力數值模擬結果與實驗結果隨藥氧比的變化趨勢相同,準靜態壓力數值模擬結果均比實驗結果高,原因是數值仿真模型的壁面為剛性壁面,屬于完全密封的狀態,而實際的實驗裝置不可能做到完全密封。

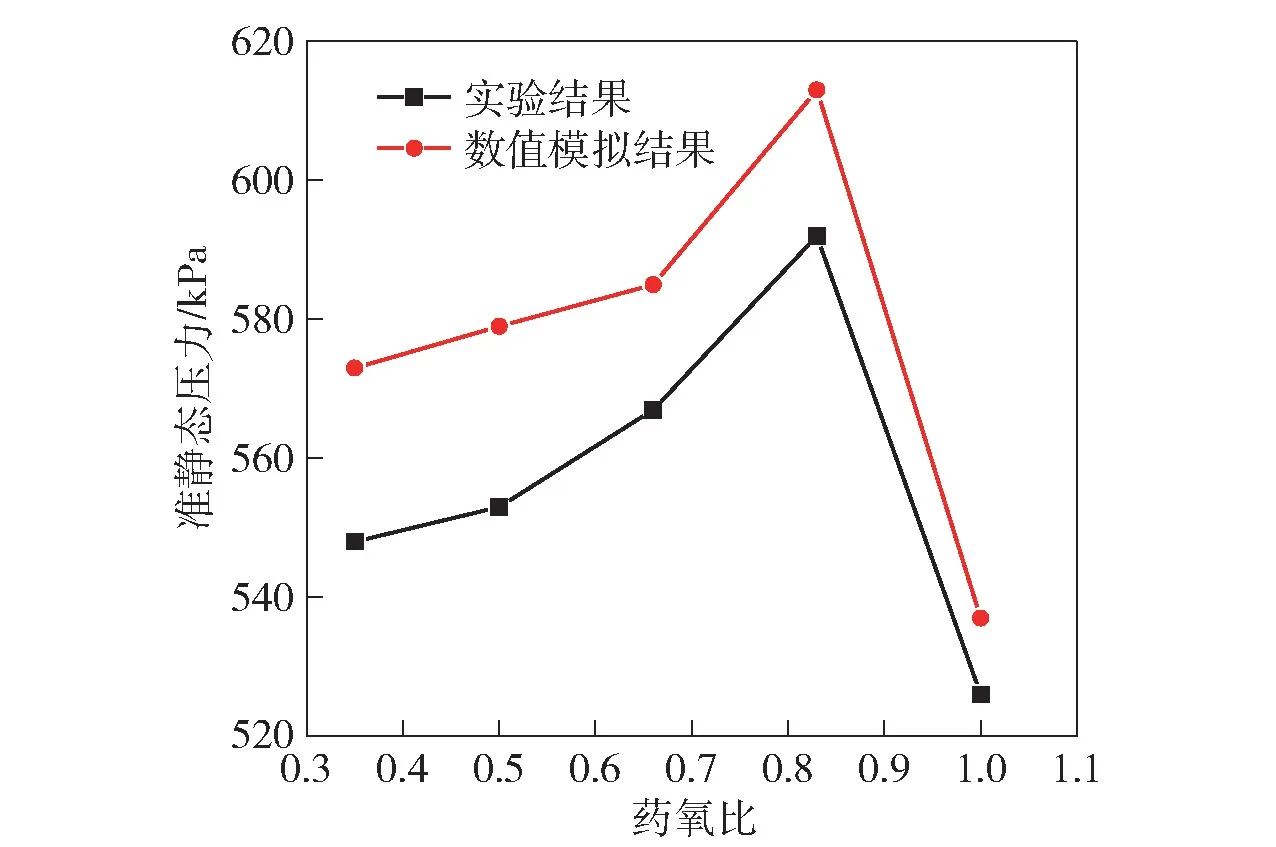
圖11 不同藥氧比樣品準靜態壓力變化Fig.11 Variation quasi-static pressure of explosive sample with R e

3.3 密閉爆炸容器形狀和體積對準靜態壓力的影響

為研究復合炸藥在不同形狀密閉爆炸容器中的準靜態壓力,分別建立500 L的立方體模型和球型模型,如圖12所示。

圖12 不同形狀密閉爆炸容器模型Fig.12 Confined explosion vessel models

以不同藥氧比炸藥-3為例計算其壓力。計算獲得炸藥密閉空間爆炸的壓力-時間曲線如圖13所示。由圖13可知,球型模型對稱性更好,其壓力時程曲線趨于平衡的過程更規律。

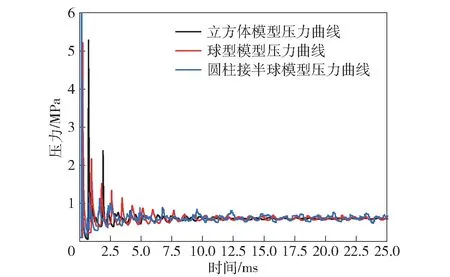
圖13 不同模型壓力曲線Fig.13 Pressure curves for different confined explosion vessel models

表8所示為不同形狀密閉爆炸容器的準靜態壓力仿真計算值。由表8可知,不同形狀的密閉爆炸容器中準靜態壓力的最大偏差為3.2%,在炸藥樣品相同、密閉空間體積相等條件下,密閉爆炸容器形狀對炸藥爆炸的準靜態壓力影響很小。

表8 不同模型下的準靜態壓力Tab.8 Quasi-static pressures under different confined explosion vessel models

進一步研究密閉爆炸容器體積對復合炸藥爆炸準靜態壓力的影響。以不同藥氧比炸藥-3為例,固定炸藥質量為100 g,采用3.2節中的仿真模型,分別建立0.10～0.50 m不同體積的密閉空間炸藥爆炸仿真模型。計算得到不同密閉空間體積條件下炸藥內爆產生的準靜態壓力,如圖14所示,可見當炸藥樣品一定時,準靜態壓力隨密閉空間體積的增加呈線性反比衰減,即為

圖14 R e-3在不同體積下的準靜態壓力Fig.14 Quasi-static pressures of R e-3 in different confined explosion vessels

4 結論

1)本文研究了藥氧比對500 L密閉空間內CL-20基復合炸藥爆炸準靜態壓力的影響規律,發現隨著藥氧比的增加,準靜態壓力呈現先升高后降低的趨勢,在藥氧比為0.83時準靜態壓力最大。

2)基于理想氣體絕熱模型和爆轟環境中鋁粒子氣化燃燒動力學方程,計算獲得復合炸藥在20 ms內釋放的能量,與準靜態壓力測試數據的趨勢基本相同,給出了準靜態壓力變化規律的機理解釋。

3)應用AUTODYN軟件建立炸藥內爆有限元模型,模擬密閉容器內炸藥爆炸作用過程,結果表明準靜態壓力計算值與實驗結果吻合良好,最大相對偏差為4.7%;密閉爆炸容器形狀對準靜態壓力影響很小;準靜態壓力隨密閉空間體積的增加呈線性反比衰減。