裸態平底榴彈底向下垂直跌落時彈丸和引信的沖擊特性

金路軒,聞泉,王雨時,王光宇,張志彪

(南京理工大學 機械工程學院,江蘇 南京 210094)

0 引言

對于彈藥勤務處理的研究一直是國防領域至關重要的工作。從裝配出廠到起爆戰斗部為止,引信要經受許多環境。在裝卸、搬動、運輸和裝填過程中,由于偶然跌落,引信、彈丸、定裝式全彈或包裝箱就會與地面或艦船甲板等目標發生碰撞,輕則影響彈藥的使用性能,重則降低安全性甚至發生意外爆炸,造成人員傷亡。跌落高度和跌落目標對引信跌落安全性影響非常明顯,為檢驗引信在勤務處理中的跌落安全性,國家軍用標準GJB 573A—1998 引信環境與性能試驗方法中規定了裸態全備引信或裝有全備引信的彈丸以規定的高度向鋼板和其他可信目標跌落的試驗方法。

引信跌落所產生沖擊作用力的波形、峰值和作用時間會隨著彈丸和引信的質量、結構、材料、跌落高度、碰擊姿態以及地面或其他跌落目標的性質等因素的不同而不同。跌落沖擊是一種復雜的非線性瞬態響應過程,采用理論建模和數值分析的可能性不大,而傳統跌落試驗也存在著諸多問題:一是由于測試歷程時間短,難以對試驗過程中的特征進行提取,無法觀察到引信內部特性;二是跌落姿態即碰撞角度難以控制,可重復性差,且難以出現完全垂直跌落的極端情況;三是試驗準備周期長、費用高、數據測定困難。文獻[5]以某型引信冗余保險系統為例,對其進行了不同落高、不同介質(水泥、瀝青、土壤和鋼板)的45°傾斜跌落試驗,并在此基礎上建立了冗余保險系統動力學模型進行數值仿真,其研究結果表明:該機構在1.5 m 高度下跌落具有較高的安全性。文獻[6]運用有限元分析ANSYS/LS-DYNA 軟件對裸態彈丸底向下跌落時的沖擊特性進行仿真,總結了裸態彈丸跌落的沖擊特性規律,其研究結果表明:同種彈丸、同種材質的跌落目標,跌落沖擊時間不隨彈丸跌落高度變化而變化,引信跌落沖擊峰值與跌落高度的算數平方根近似呈正比。文獻[7]以105 mm 口徑彈丸為仿真對象,研究了彈丸以不同姿態跌落至不同介質時彈頭引信和彈底引信受到的跌落沖擊脈沖峰值和寬度。研究結果表明:無論是彈頭向上還是彈頭向下姿態跌落,彈底引信的跌落沖擊脈沖峰值都低于彈頭引信。文獻[8]對箱裝彈藥的跌落沖擊過程進行了仿真研究,并進行了試驗驗證,其結果表明:箱裝彈藥以小角度傾斜跌落地面不會降低彈丸的安全性,可以將堆摞箱數增加至4 箱。雖然已有相關文獻采用有限元方法研究了裸態彈丸以不同高度底向下垂直跌落碰撞不同地面目標時作用于引信上的沖擊過載特性,但未見有對此過程建立彈塑性模型推導出沖擊特性公式的文獻。

針對上述問題,本文采用理論推導結合有限元仿真對裸態彈丸底向下垂直跌落碰撞不同地面目標時彈丸和引信的沖擊特性進行系統性總結。

1 裸態彈丸底向下垂直跌落碰撞地面目標沖擊特性理論公式

1.1 碰撞模型的建立

假設彈丸跌落碰撞的地面目標為彈性半空間體,彈丸質量為,彈丸直徑為,彈底直徑為,彈體和地面目標的彈性模量分別為和,泊松比分別為和,彈丸與地面目標碰撞中產生的接觸壓力為,彈丸跌落地面目標示意圖如圖1 所示。為簡化分析,將彈丸看作是一個剛體,彈丸跌落過程則可看作是在直徑為的圓面積內均勻受到載荷的作用。

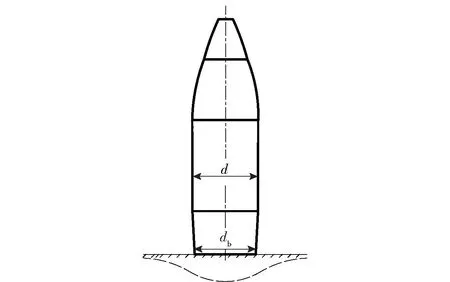
圖1 彈丸跌落地面目標示意圖Fig.1 Schematic diagram of projectile dropping to the ground

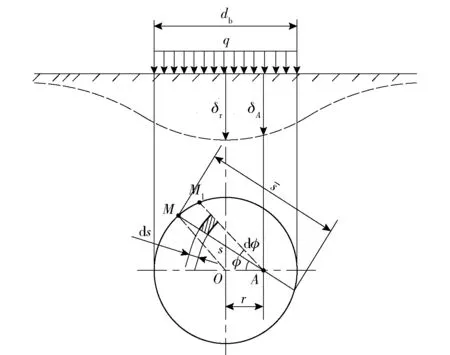
圖2 彈丸跌落沖擊地面目標時地面目標圓內任意一點A 的下沉量Fig.2 Sinkage of any point A in the ground target circle when the projectile drops and collids the ground target

d上的壓力為

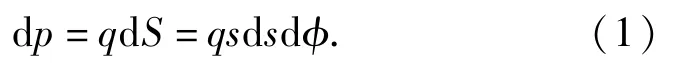
應用疊加法推導出圓形均勻載荷作用下引起的點下沉量,由微元面積d上壓力引起的點下沉量為

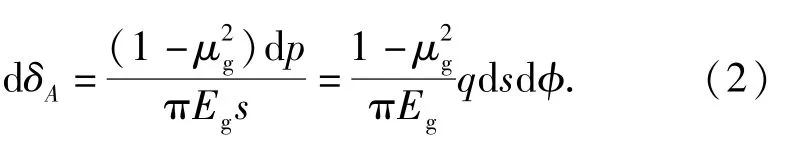
由總壓力引起的點下沉量為

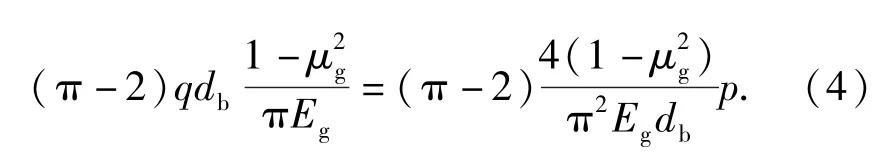
考慮彈丸的變形量,將彈丸簡化為一個整體,則總下沉距離為

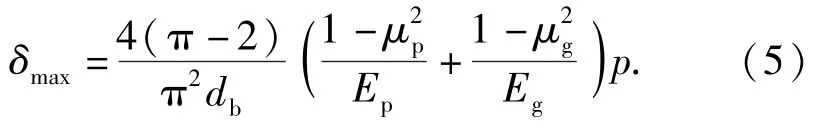
1.2 理論公式推導

文獻[10]詳細描述了彈丸的跌落沖擊過程。彈丸與地面目標碰撞,接觸壓力使彈丸減速運動,設彈丸的速度為,根據牛頓第二定律建立微分運動方程:

彈丸與地面目標的相對速度為

將(7)式兩邊對時間求導,

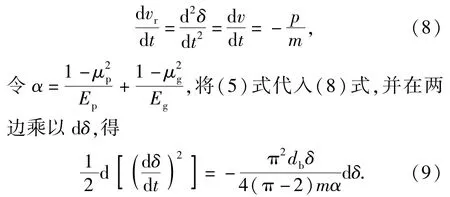
令碰撞開始時彈丸與靶板的相對速度為,開始碰撞進行壓縮時的相對速度為=dd,將(9)式積分,得

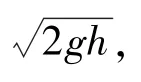
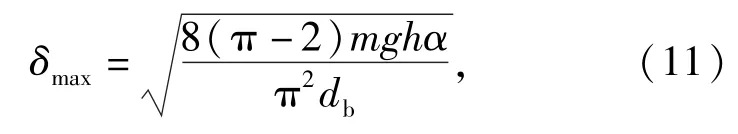
令(5)式與(11)式相等,即

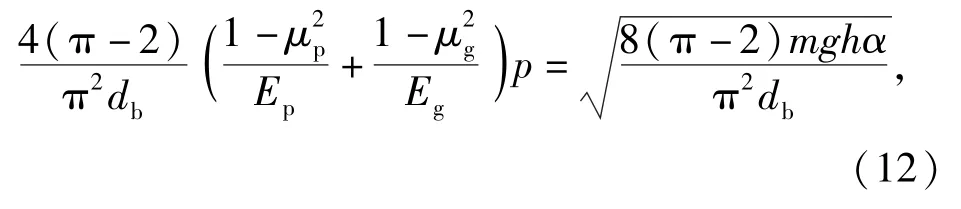
進而可以得到彈丸跌落產生的沖擊加速度峰值為

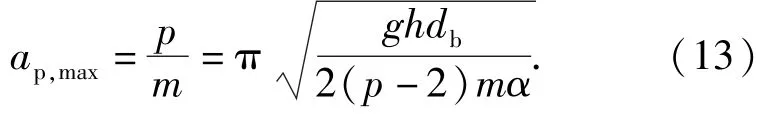
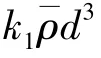
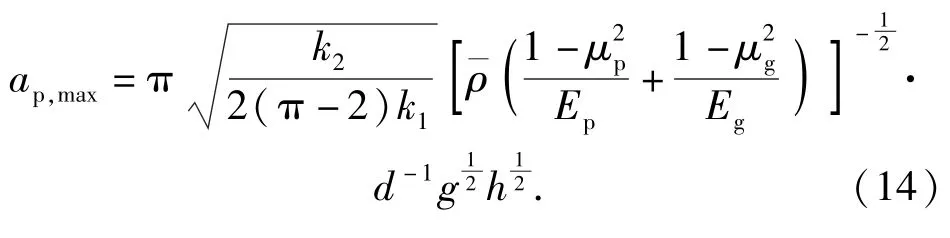
從(14)式中可以看出,彈丸與地面目標碰撞,彈丸的沖擊加速度峰值與跌落高度的算術平方根呈正比,與彈丸直徑呈反比。

由(10)式可得

彈丸跌落地面目標是一個非彈性碰撞過程,假設彈體與地面目標之間的碰撞恢復系數為,無量綱,則碰撞恢復時間為

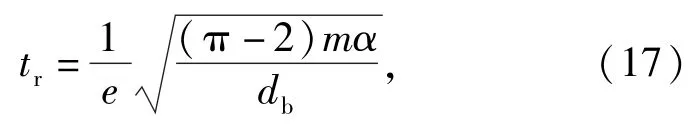
則總沖擊作用時間為

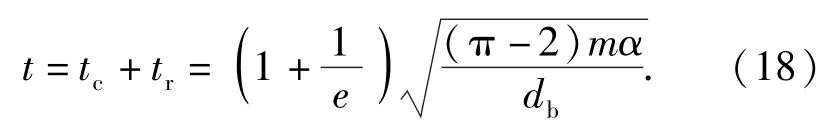
同(13)式、(14)式的推導方法進行化簡,可得到

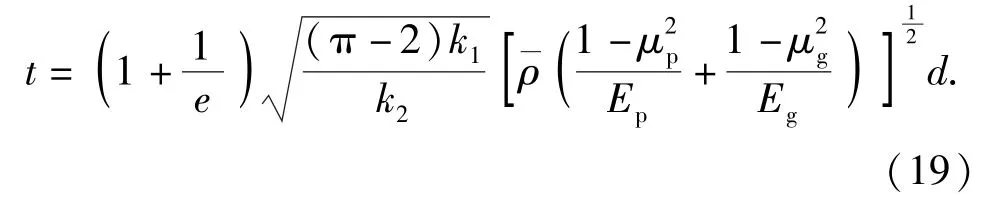
從(19)式中可以看出,彈丸與地面目標碰撞,彈丸沖擊作用時間與彈丸直徑呈正比,與跌落高度無關。

(14)式和(19)式即為裸態彈丸底向下垂直跌落碰撞地面目標時,彈丸整體沖擊加速度峰值與沖擊作用時間的理論推導公式。

2 彈丸底向下垂直跌落碰撞地面目標時的彈丸和引信沖擊特性仿真

2.1 建立有限元模型

為了對第1 節的理論推導公式進行驗證,選擇某152 mm 口徑榴彈作為仿真對象,建立裸態彈丸垂直跌落有限元模型。由于彈丸和引信結構復雜,為減少計算時間,將模型進行簡化配重處理,簡化后的彈丸模型如圖3 所示。

圖3 152 mm 口徑榴彈簡化模型Fig.3 Simplified model 152 mm caliber HE-projectile

參照國家軍用標準GJB 537A—1998 引信環境與性能試驗方法中的104 要求,裝有全備引信的試驗彈或裸態的全備引信跌落到鋼板上,鋼板最小厚度為75 mm,布氏硬度不低于200,且應牢固地安裝在厚度不小于0.6 m 的混凝土基座上。鋼板表面必須平整,長、寬尺寸至少為試驗彈最大尺寸的1.0～1.5 倍。文獻[6]仿真表明,有無混凝土基座對跌落沖擊峰值和沖擊時間基本無影響,故本文仿真為節省機時省略了混凝土基座。因為裸態彈丸最大尺寸為707 mm,所以設置跌落目標靶板長、寬均為1 062 mm。國家軍用標準GJB 573A—1998 引信環境與性能試驗方法中除了規定1.5 m 高度跌落試驗外,還規定可采用其他高度及對除鋼板以外的地面目標進行跌落試驗。

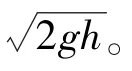
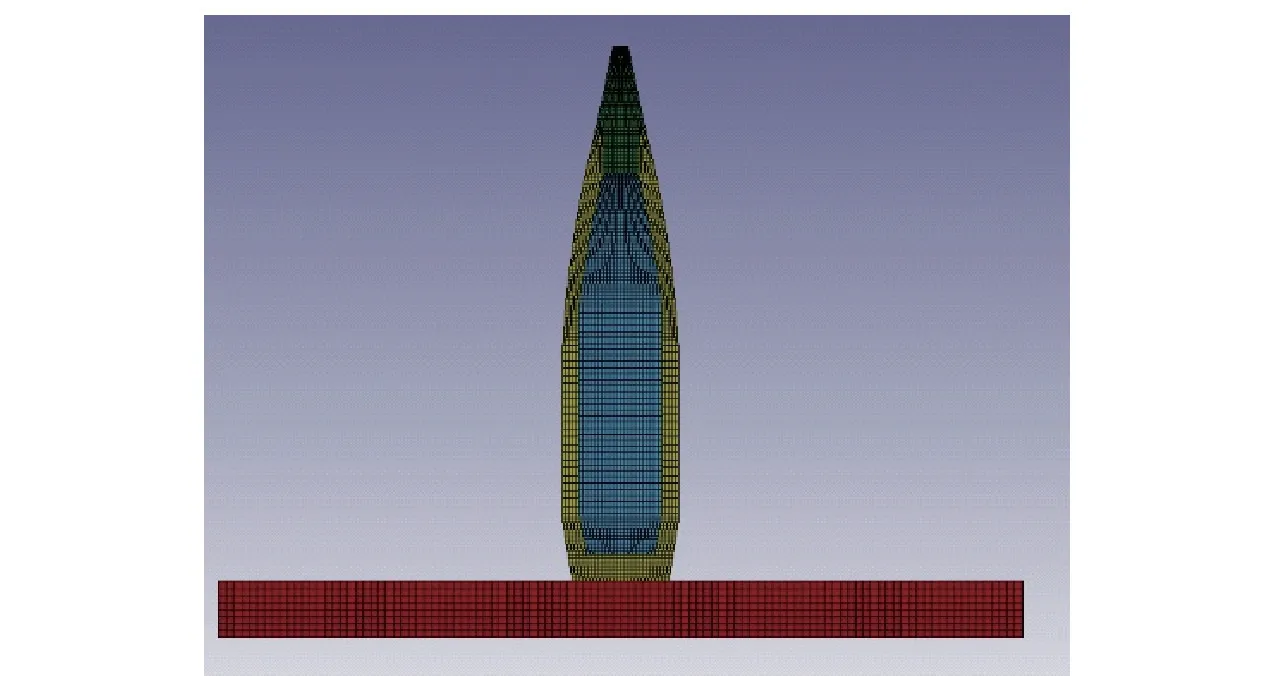
圖4 彈丸跌落有限元模型Fig.4 Finite element model of projectile dropping

引信體材料為7A04 鋁合金,彈體材料為D60 鋼。引信、彈體和鋼板采用JOHNSON_COOK 材料模型,裝藥、混凝土、紅松木板和土壤均采用PLASTIC_KINEMATIC材料模型。各材料仿真參數如表1 所示,152 mm 口徑彈丸相關參數如表2 所示。

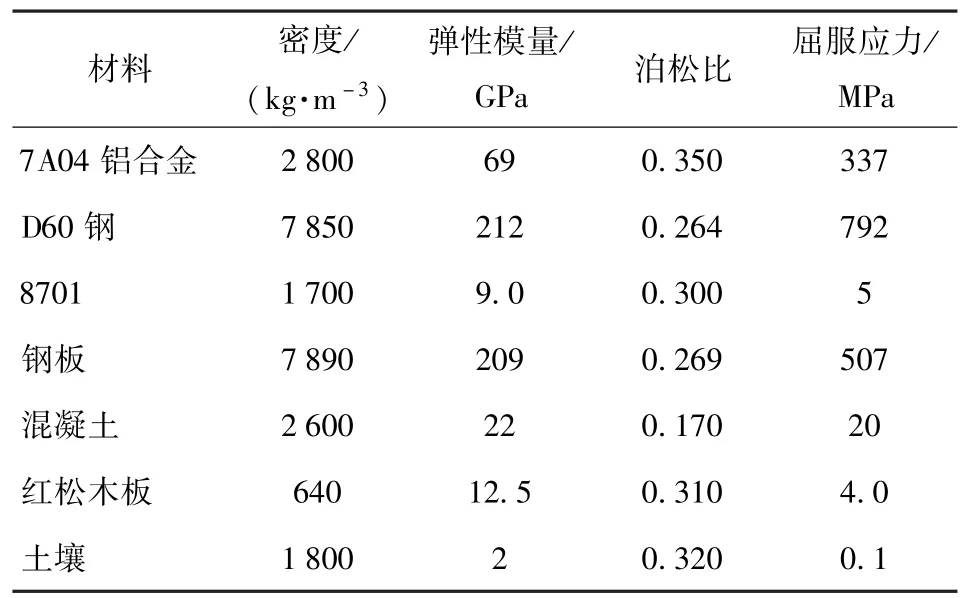
表1 各材料仿真參數[12-14]Tab.1 Simulation parameters of various materials[12-14]

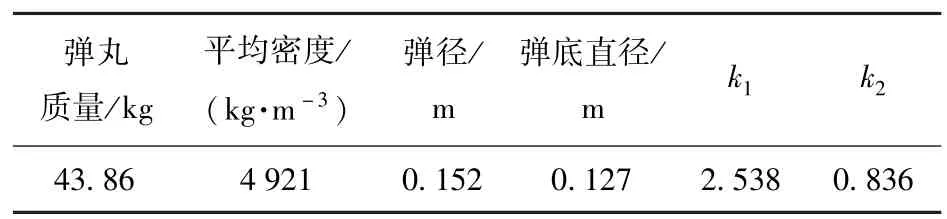
表2 152 mm 口徑彈丸相關參數Tab.2 Related parameters of 152 mm caliber projectile

2.2 彈丸跌落沖擊特性

仿真得到152 mm 口徑榴彈底向下以0.7 m、1.5 m、2.1 m、3.0 m 落高,分別垂直跌落于鋼板、混凝土、紅松木、土壤(厚度取為75 mm)時,彈丸跌落沖擊加速度峰值如表3 所示,彈丸沖擊作用時間如表4 所示。

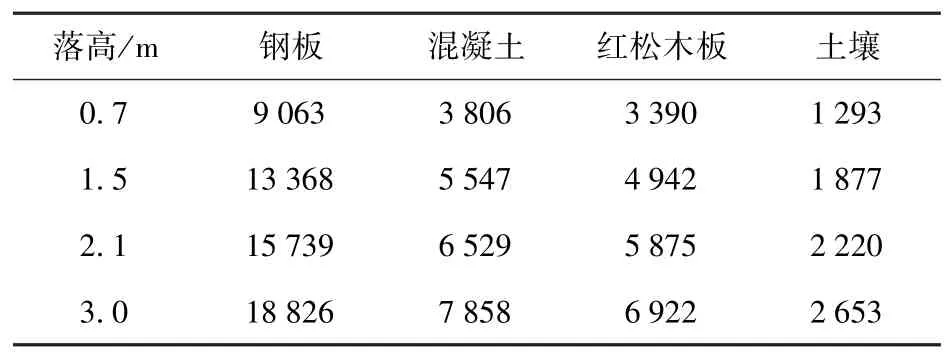
表3 152 mm 口徑彈丸以不同落高底向下垂直跌落時彈丸跌落沖擊加速度峰值Tab.3 Peak impact acceleration of 152 mm caliber projectile when vertically dropping at different heights g

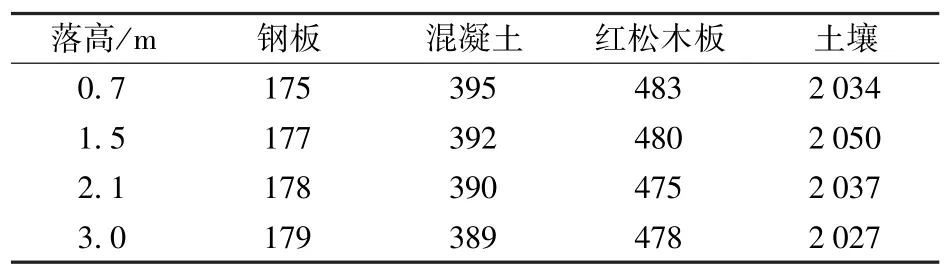
表4 152 mm 口徑彈丸以不同落高底向下垂直跌落時彈丸跌落沖擊作用時間Tab.4 Impact duration of 152 mm caliber projectile when vertically dropping at different heights μs

從表3 和表4 中可以看出:裸態彈丸以同一高度跌落時,彈丸沖擊峰值隨跌落介質硬度增大而增大,跌落沖擊時間隨著跌落介質硬度增大而減小;不同高度跌向同一介質時,彈丸跌落沖擊峰值隨跌落高度增大而增大,跌落沖擊時間基本不隨高度變化而變化。

由于受飛行穩定性限制,旋轉彈丸彈形和長徑比相差不太大,可將該152 mm 口徑榴彈彈丸等比例縮小成為122 mm、85 mm、57 mm、37 mm、20 mm共5 種口徑榴彈彈丸(由于彈丸質量與彈丸直徑的3 次方呈比例,質量也相應減小),分別從不同高度跌落至鋼板、混凝土、紅松木板和土壤,彈丸跌落沖擊加速度峰值仿真結果如表5 所示。

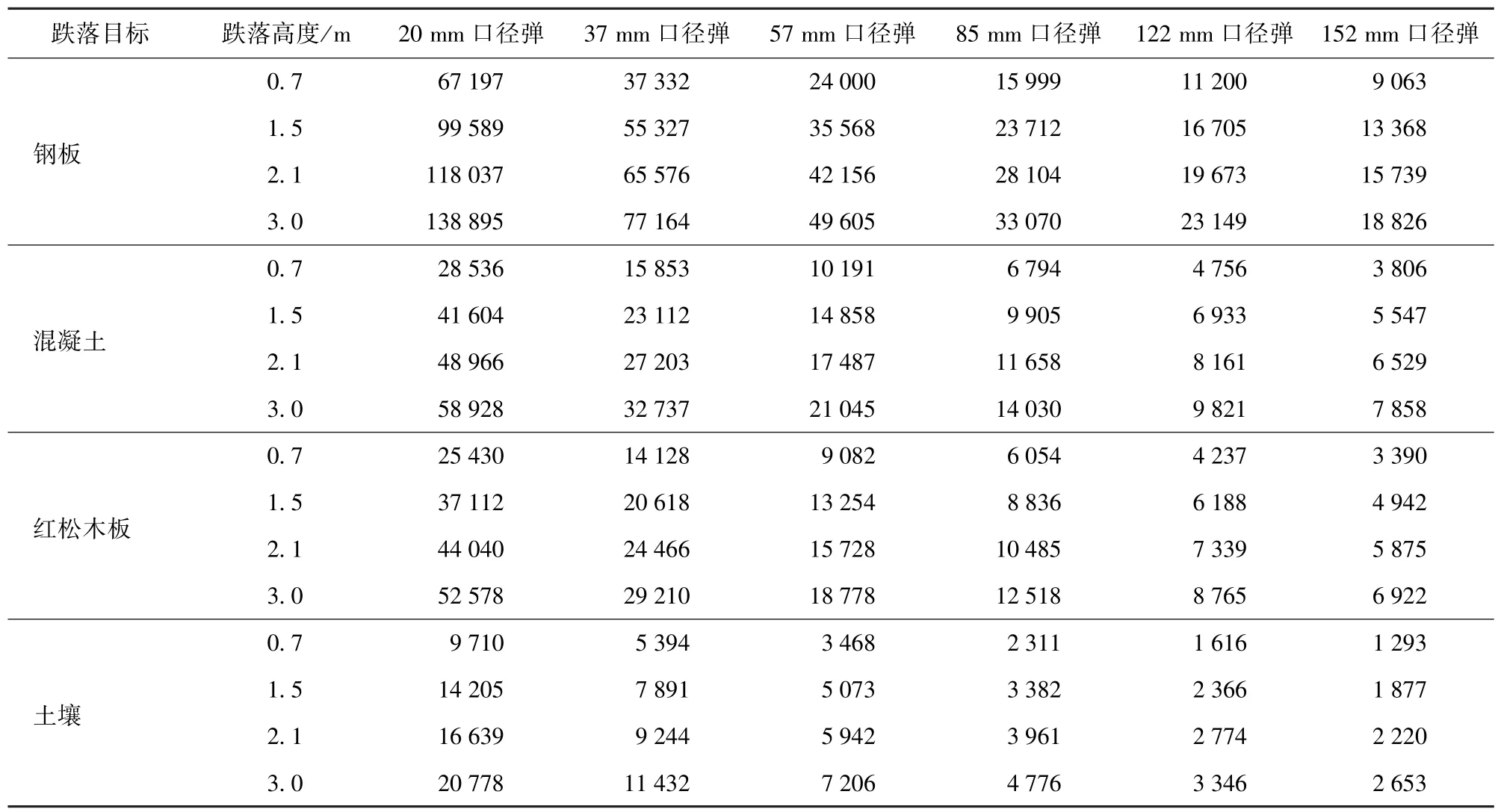
表5 不同口徑彈丸以不同高度垂直跌落于不同地面目標時的彈丸沖擊加速度峰值Tab.5 Peak impact acceleration of projectiles with different calibers dropping vertically on different ground targets at different heights g

比較表5 中的數據可以看出,在彈形相同條件下,彈丸以相同跌落高度跌落同一地面目標時,跌落沖擊峰值隨著彈丸直徑的增大而減小。

為了初步驗證彈丸跌落沖擊特性理論公式的可信性,引入一個加速度修正系數,假設彈丸跌落時產生的沖擊加速度峰值為

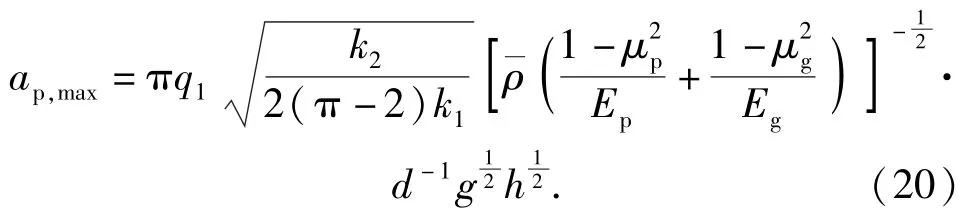
將表1 和表2 中各參數代入(20)式進行擬合,表6 為通過理論公式計算并擬合得到的加速度修正系數。由表6 可知,彈丸跌落至地面目標的沖擊加速度峰值理論修正公式中加速度修正系數可取0.884～1.027 0,平均值為0.94這主要是由于在計算彈丸跌落變形量時將彈丸簡化為一個整體,取為彈體彈性模量而不是彈丸平均彈性模量,從而導致偏大,彈丸最大加速度計算值偏高,修正系數值偏小。將該平均值代入(20)式,可以得到彈丸跌落地面目標時的沖擊加速度峰值修正公式為

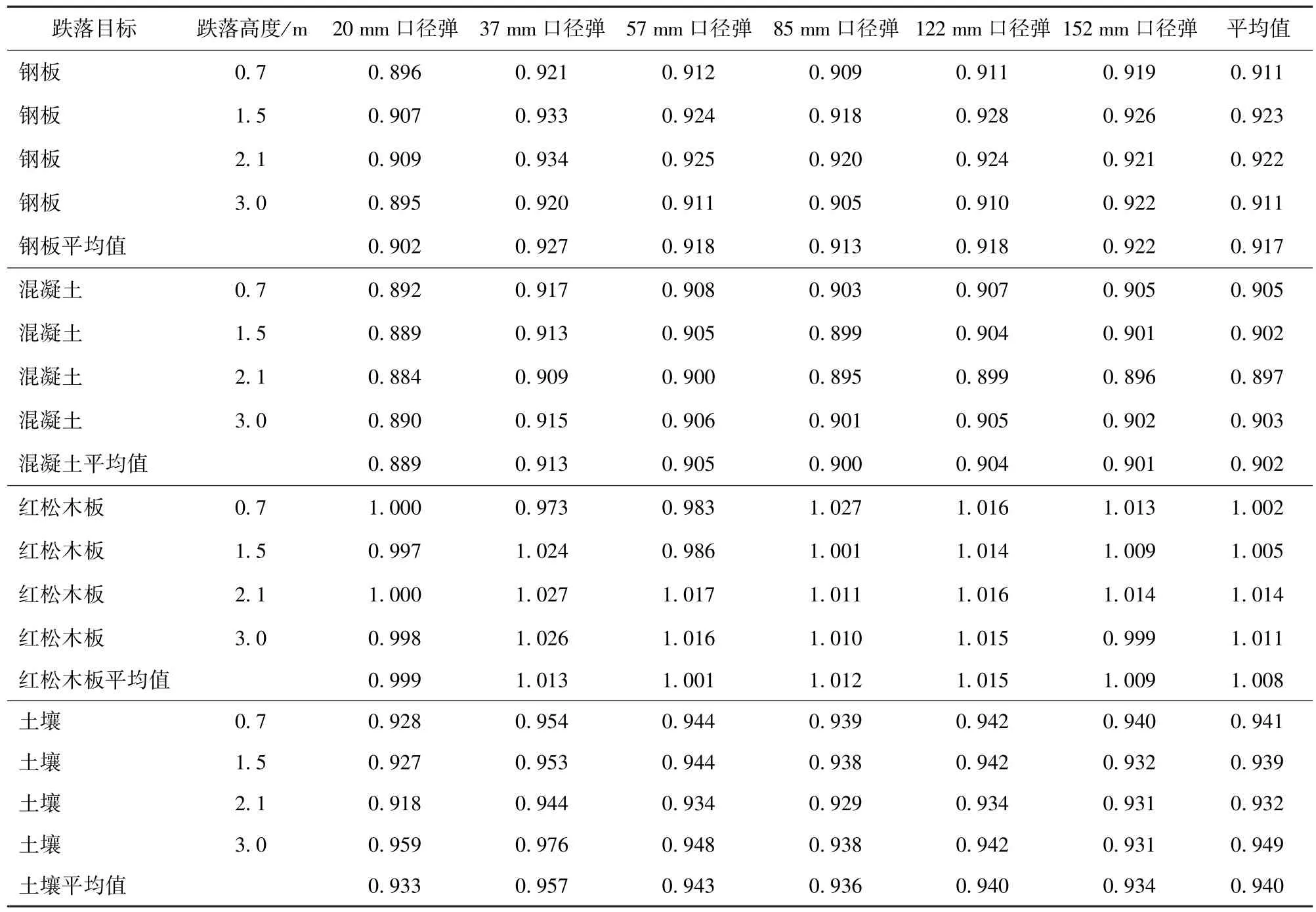
表6 通過理論公式擬合得到的加速度修正系數q1Tab.6 Acceleration correction coefficients q1 obtained by fitting the theoretical formula

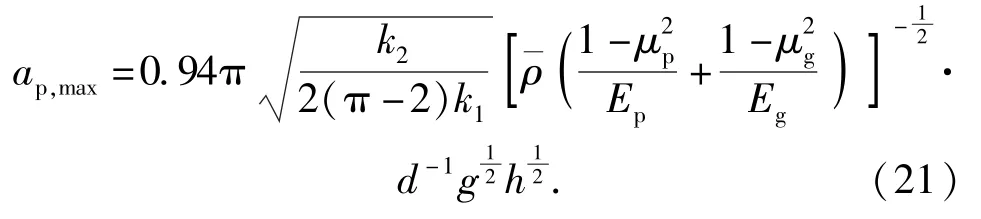
6 種不同口徑彈丸從不同高度跌落至鋼板、混凝土、紅松木板和土壤時,彈丸的跌落沖擊作用時間仿真結果如表7 所示。

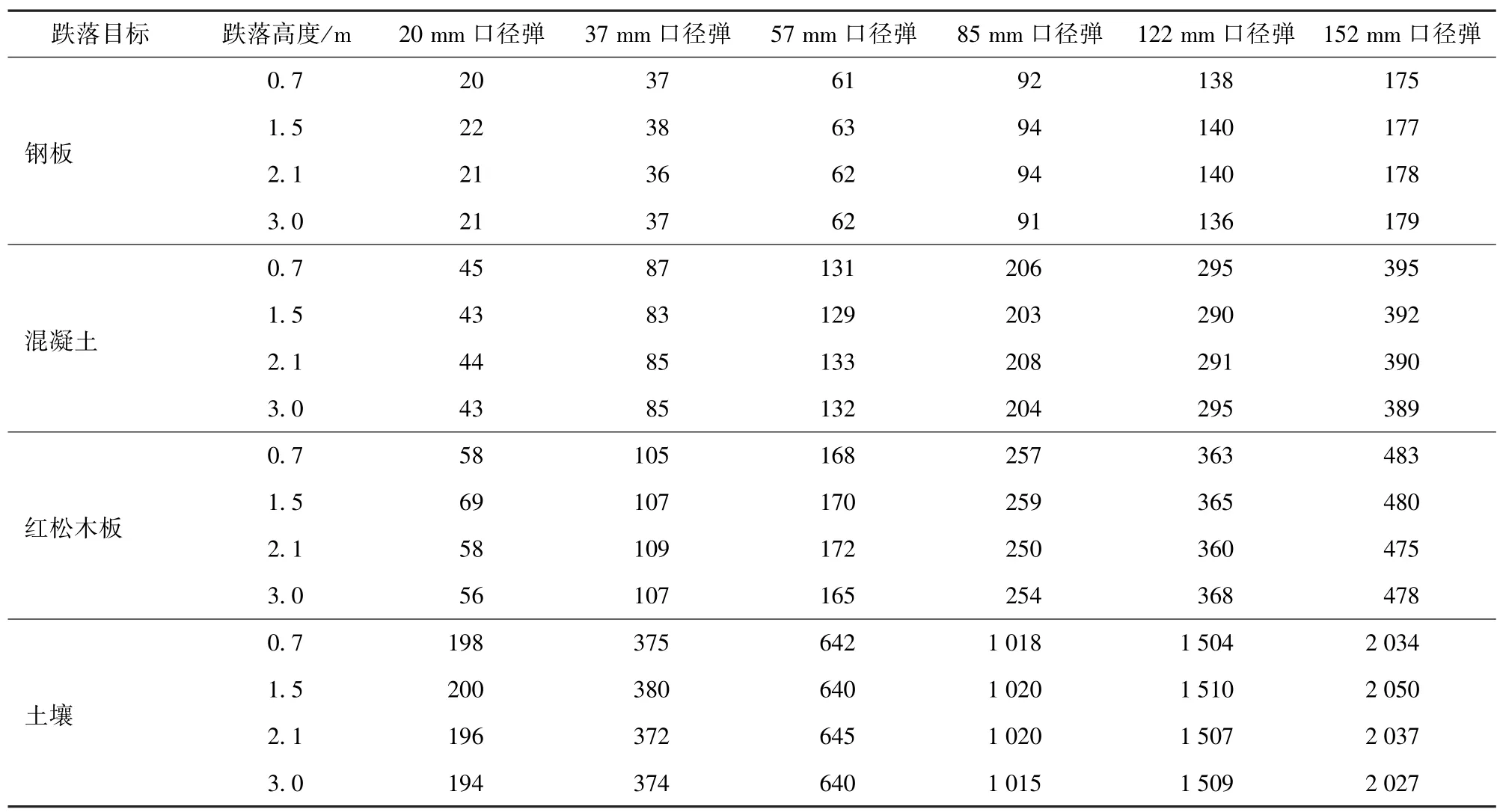
表7 不同口徑彈丸以不同高度垂直跌落于不同地面目標時的沖擊作用時間Tab.7 Impact duration of projectiles with different calibers dropping vertically on different ground targets at different heights μs

從表7 中可以看出:同種彈丸跌落至同一地面目標時,沖擊作用時間基本不隨高度的變化而變化,與文獻[6]仿真得到的結論基本相同;在彈形相同條件下,彈丸以相同跌落高度跌落同一地面目標時,沖擊作用時間隨著彈丸直徑的增大而增大。

同理引入一個沖擊時間修正系數,假設彈丸跌落時產生的沖擊作用時間為

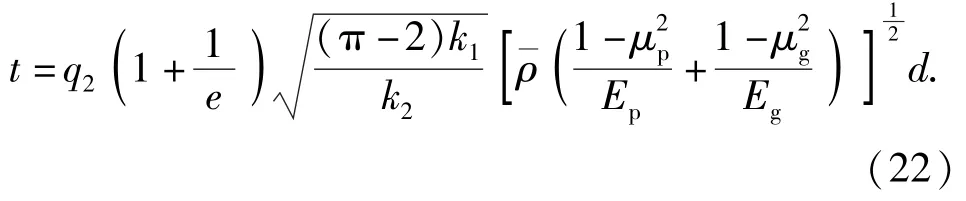
對彈丸跌落地面目標全過程進行分析,根據動量守恒定理,得

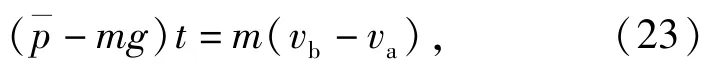
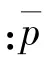
彈丸碰撞地面目標時產生的平均接觸壓力遠大于重力,因此通常忽略重力的影響,(23)式可化簡為

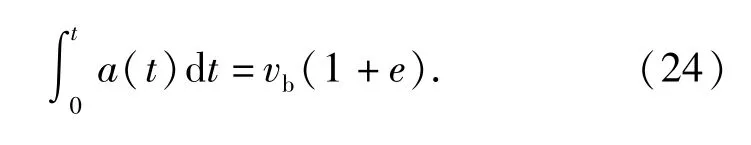
對仿真得到的彈丸跌落沖擊加速度曲線()進行積分并利用(24)式進行計算,可求出此次不同口徑彈丸跌落鋼板、混凝土、紅松木和土壤的碰撞恢復系數。表8 為不同口徑彈丸以1.5 m 高度垂直跌落碰撞不同地面目標時的碰撞恢復系數。由表8可以看出:對于彈丸以同一高度跌落碰撞同種地面目標,碰撞恢復系數隨著彈丸口徑的增大而減小;沖擊作用時間基本不隨高度變化而變化,因此對同一彈丸以不同高度跌落得到的沖擊時間取平均值。

表8 不同口徑彈丸以1.5 m 高度垂直跌落碰撞不同地面目標時的碰撞恢復系數Tab.8 Collision recovery coefficients of different caliber projectiles colliding with different ground targets

將表1 和表2 中各參數代入(22)式進行擬合,正系數。

由表9 可以看出,彈丸跌落地面目標時產生的表9 為通過理論公式計算并擬合得到的沖擊時間修沖擊作用時間理論修正公式中系數可取1.005～1.070,平均值為1.04。由于取為彈體彈性模量而不是彈丸平均彈性模量,從而導致偏大,彈丸沖擊時間計算值偏短,修正系數值偏大。將該平均值代入(22)式,可以得到彈丸跌落地面目標的沖擊作用時間修正公式為

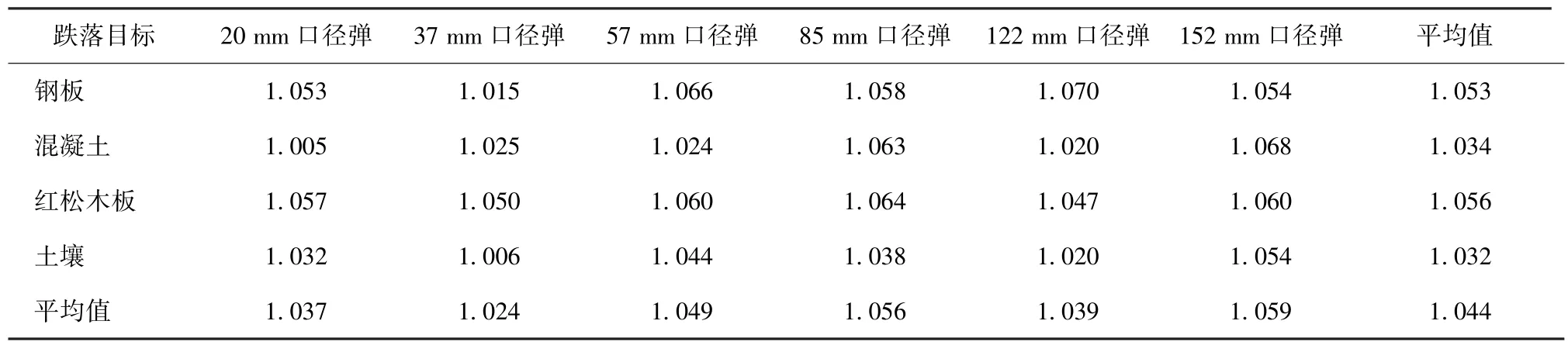
表9 通過理論公式擬合得到的時間修正系數q2Tab.9 Time correction coefficients q2 obtained by fitting the theoretical formula

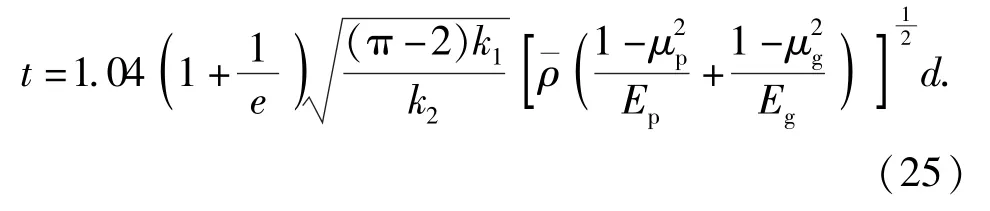
(21)式和(25)式即為彈丸跌落地面目標時沖擊加速度峰值與沖擊作用時間的修正公式,從中可以發現,通過仿真得到彈丸沖擊特性規律與通過理論推導得到的彈丸跌落沖擊特性規律相近,即沖擊加速度峰值與彈丸直徑和跌落高度有關,沖擊作用時間與彈丸直徑有關而與跌落高度無關,可認為彈丸沖擊特性理論公式通過修正具有一定可信性。

2.3 彈丸跌落時的引信沖擊特性

6 種不同口徑彈丸從不同高度跌落至鋼板、混凝土、紅松木板和土壤,其引信跌落沖擊加速度峰值仿真結果如表10 所示,跌落沖擊作用時間仿真結果如表11 所示。

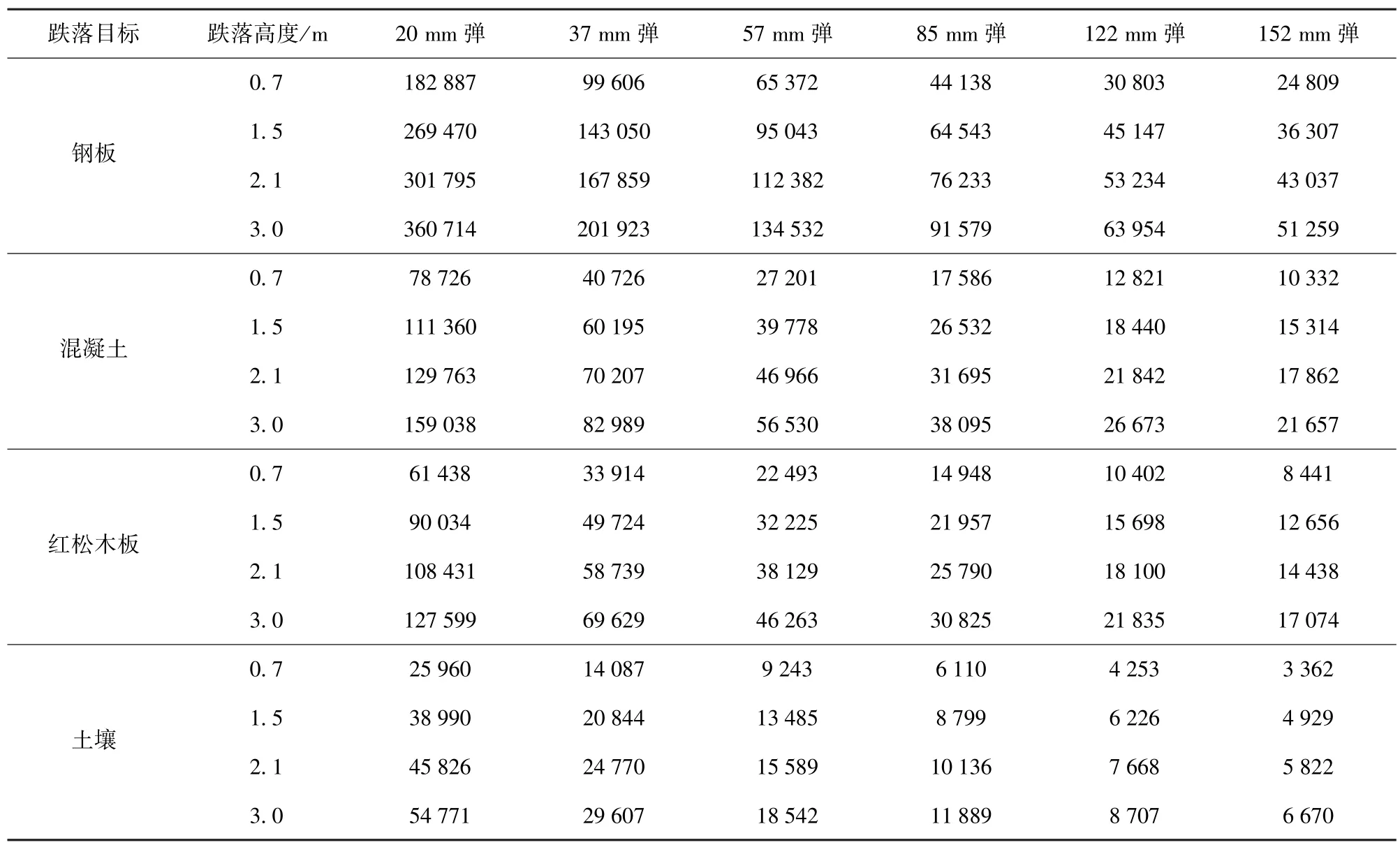
表10 不同口徑彈丸以不同高度垂直跌落于不同地面目標時的引信沖擊加速度峰值Tab.10 Peak fuze impact acceleration of different caliber projectiles dropping on different ground targets at different heights g

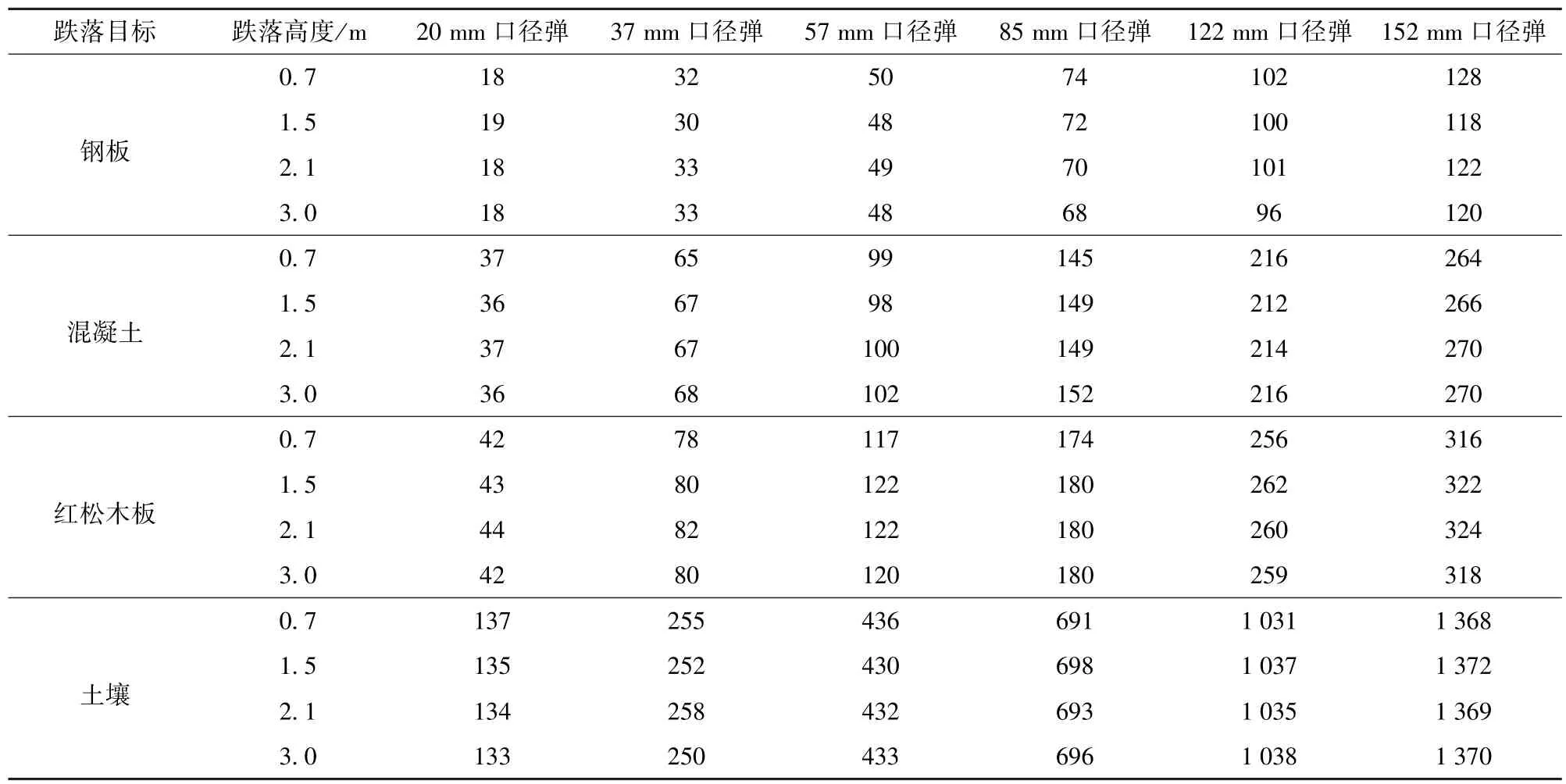
表11 不同口徑彈丸以不同高度垂直跌落于不同地面目標的引信沖擊作用時間Tab.11 Fuze impact durations of different caliber projectiles dropping vertically on different ground targets at different heights μs

由表10 和表11 中可以看出,通過仿真得到引信沖擊特性規律與彈丸跌落沖擊特性規律相近,下面將擬合得到彈丸底向下垂直跌落時引信沖擊特性的計算公式。

假設引信跌落加速度峰值與彈丸跌落加速度沖擊峰值呈比例關系,現引入一個新的加速度比例系數,引信跌落沖擊加速度峰值可寫為

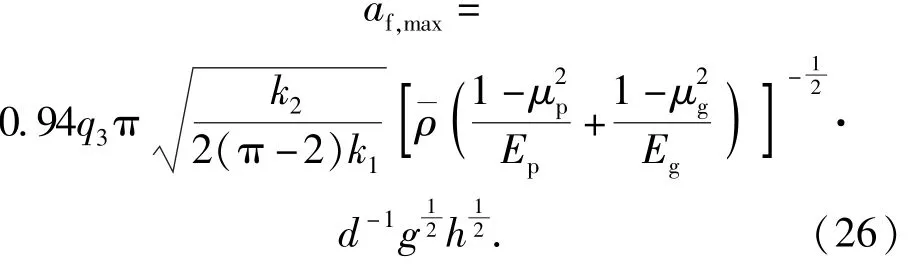
為了求得加速度比例系數,將表1 和表2 中各材料參數代入(26)式進行擬合。表12 為通過修正公式計算并擬合得到的加速度比例系數。

由表12 可知,彈丸跌落地面目標時引信的沖擊加速度峰值計算公式中比例系數可取2.400～2.759,平均值為2.61,即彈丸底向下垂直跌落至地面目標時,引信沖擊加速度峰值大約是彈丸加速度峰值的2.61倍,將該平均值代入(26)式可以得到彈丸跌落地面目標時的引信沖擊加速度峰值計算公式為

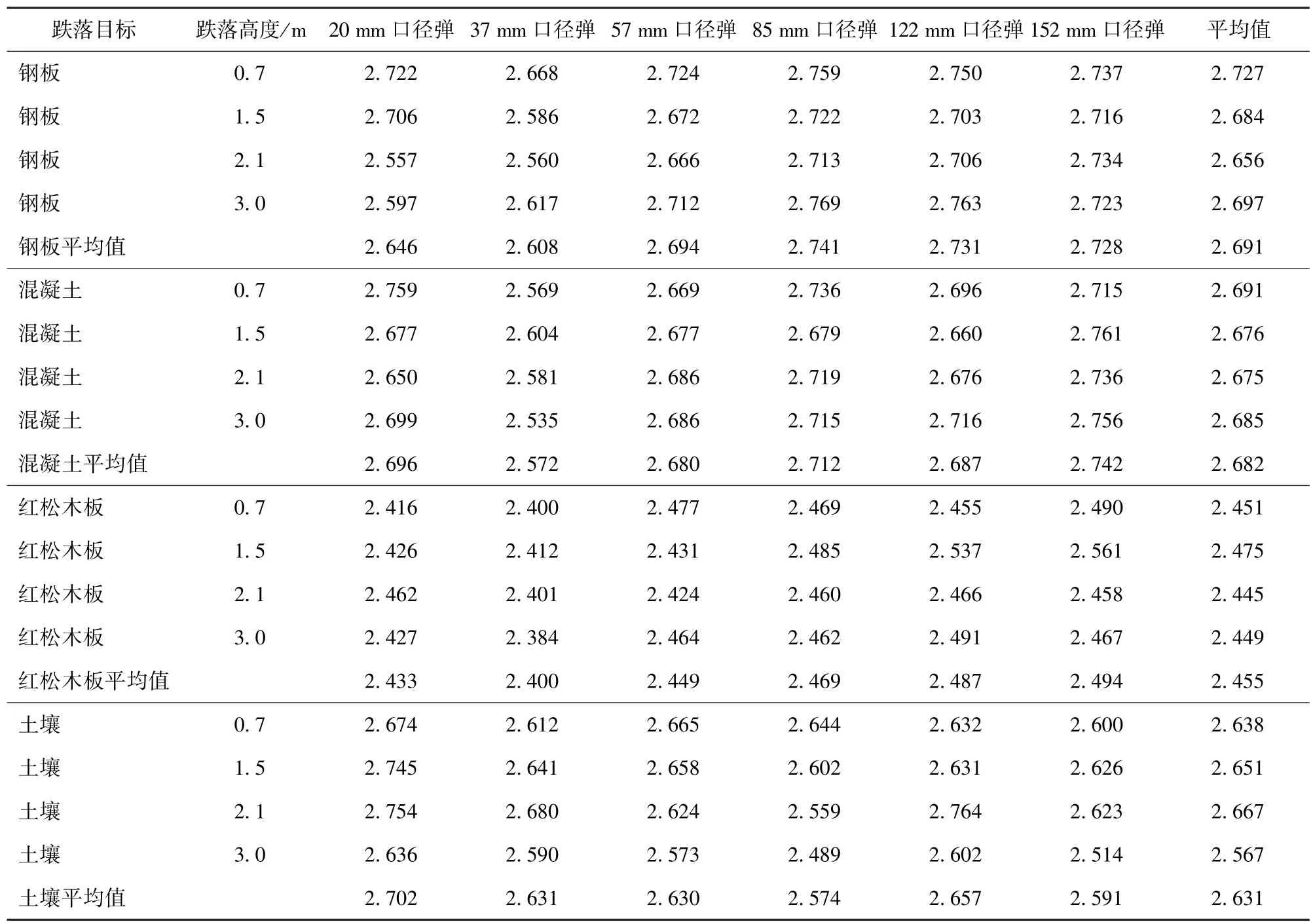
表12 通過修正公式擬合得到的加速度比例系數q3Tab.12 Acceleration proportionality coefficients q3 obtained by fitting the correction formula

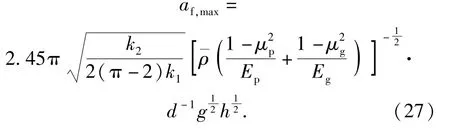
同理,假設引信跌落沖擊時間與彈丸跌落沖擊時間呈比例關系,引入一個新的沖擊時間比例系數,引信的沖擊作用時間可寫為

將表1 和表2 中各參數代入(28)式進行擬合,表13 為通過修正公式計算并擬合得到的沖擊時間比例系數。

由表13 可以看出,彈丸跌落地面目標時引信的沖擊作用時間計算公式中系數可取0.665～0.837,平均值為0.73,即彈丸底向下垂直跌落至地面目標時,引信沖擊作用時間大約是彈丸沖擊作用時間的0.73 倍。將該平均值代入(28)式可以得到彈丸跌落地面目標時的引信沖擊作用時間公式為

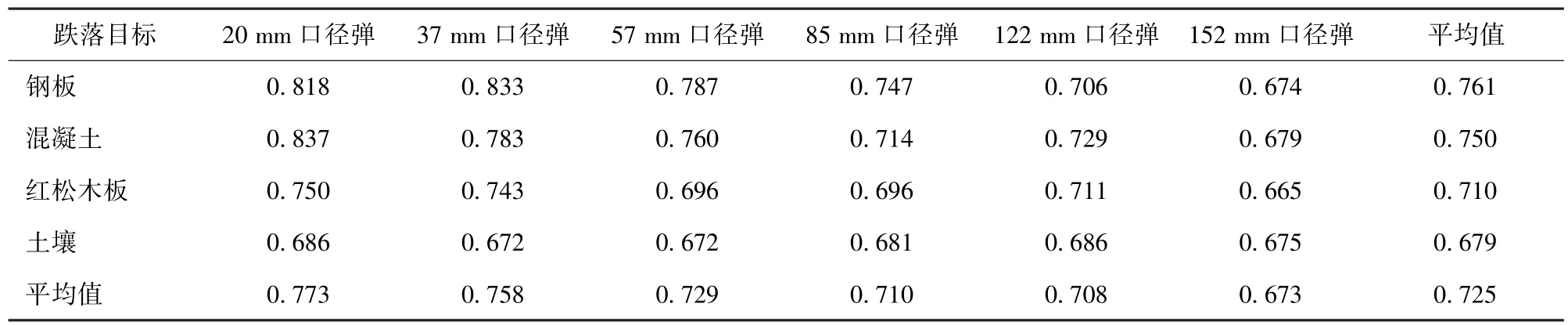
表13 通過修正公式擬合得到的沖擊作用時間比例系數q4Tab.13 Impact duration proportional coefficients q4 obtained by fitting the modified formula

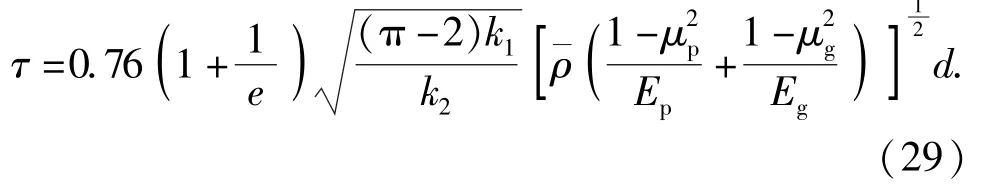
至此就得到了彈丸底向下跌落時引信沖擊加速度峰值和沖擊作用時間的計算公式。需要注意的是,該公式適用范圍為配用于平底彈丸的彈頭引信。

2.4 不同參數對引信沖擊特性的影響

從(27)式和(29)式可以看出:引信沖擊加速度峰值與彈丸平均密度、彈體的泊松比、彈體的彈性模量、地面目標的泊松比、地面目標的彈性模量、跌落高度以及彈丸直徑有關;沖擊作用時間與碰撞恢復系數、彈丸平均密度、彈體的泊松比、彈體的彈性模量、地面目標的泊松比、地面目標的彈性模量以及彈丸直徑有關。下面仍以152 mm 口徑榴彈為例,分析計算公式中各參數對引信沖擊特性的影響。

改變彈丸平均密度,采用計算公式求得彈丸以1.5 m 落高跌落鋼板時引信沖擊加速度峰值與作用時間變化,如圖5 所示。由圖5 可以看出,彈丸平均密度越大,彈丸跌落時產生的引信沖擊加速度峰值越小,相應的沖擊作用時間越長,但影響程度有限。

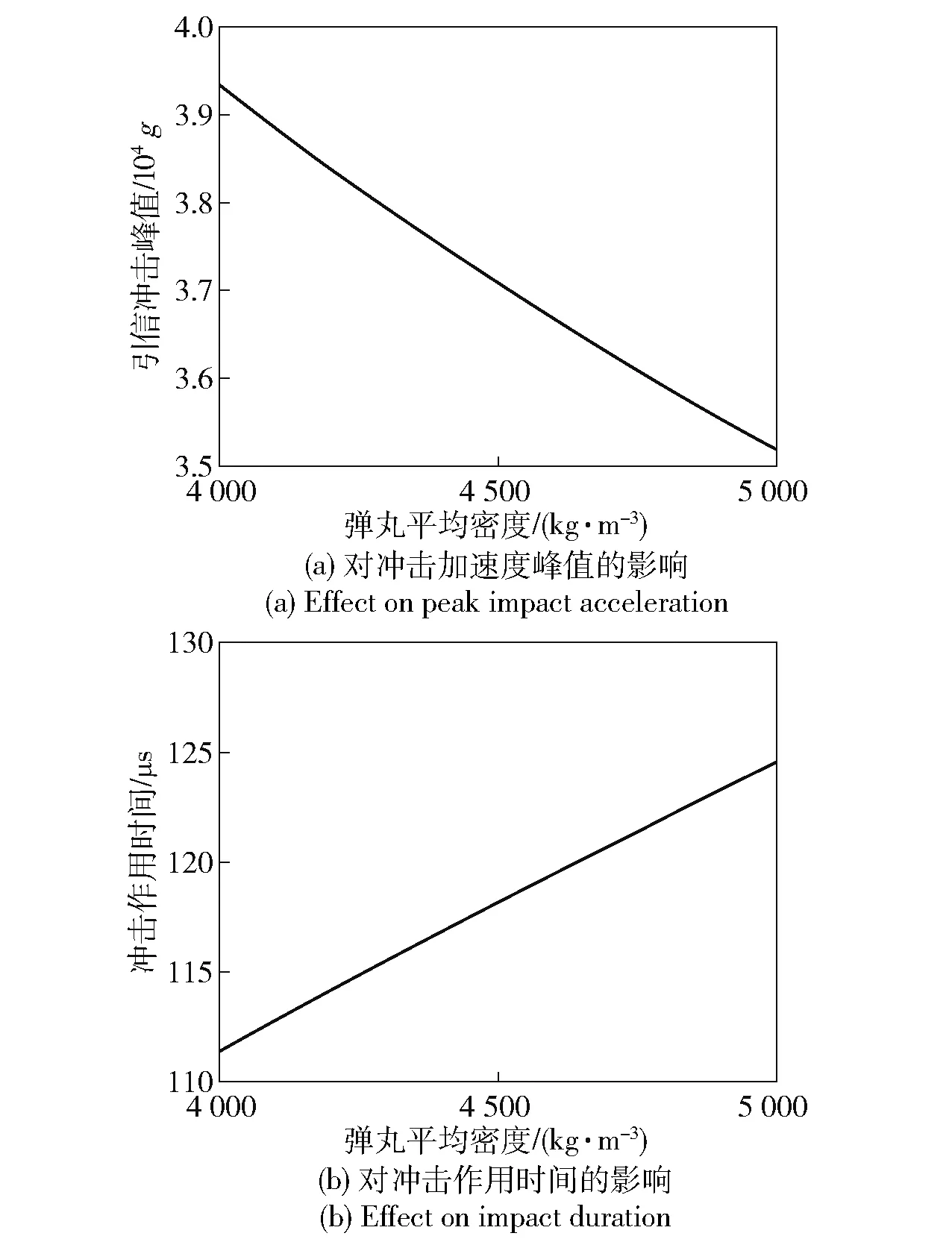
圖5 彈丸平均密度對引信沖擊特性的影響Fig.5 Effect of projectile average density on impact characteristics of fuze

通常材料的泊松比取值范圍為0～0.5,改變地面目標泊松比,采用計算公式求得彈丸以1.5 m 落高跌落鋼板時引信沖擊加速度峰值與作用時間變化,如圖6 所示。地面目標的泊松比越大,彈丸跌落時產生引信的沖擊加速度峰值越大,沖擊時間越短,但影響程度非常有限,可以忽略不計。

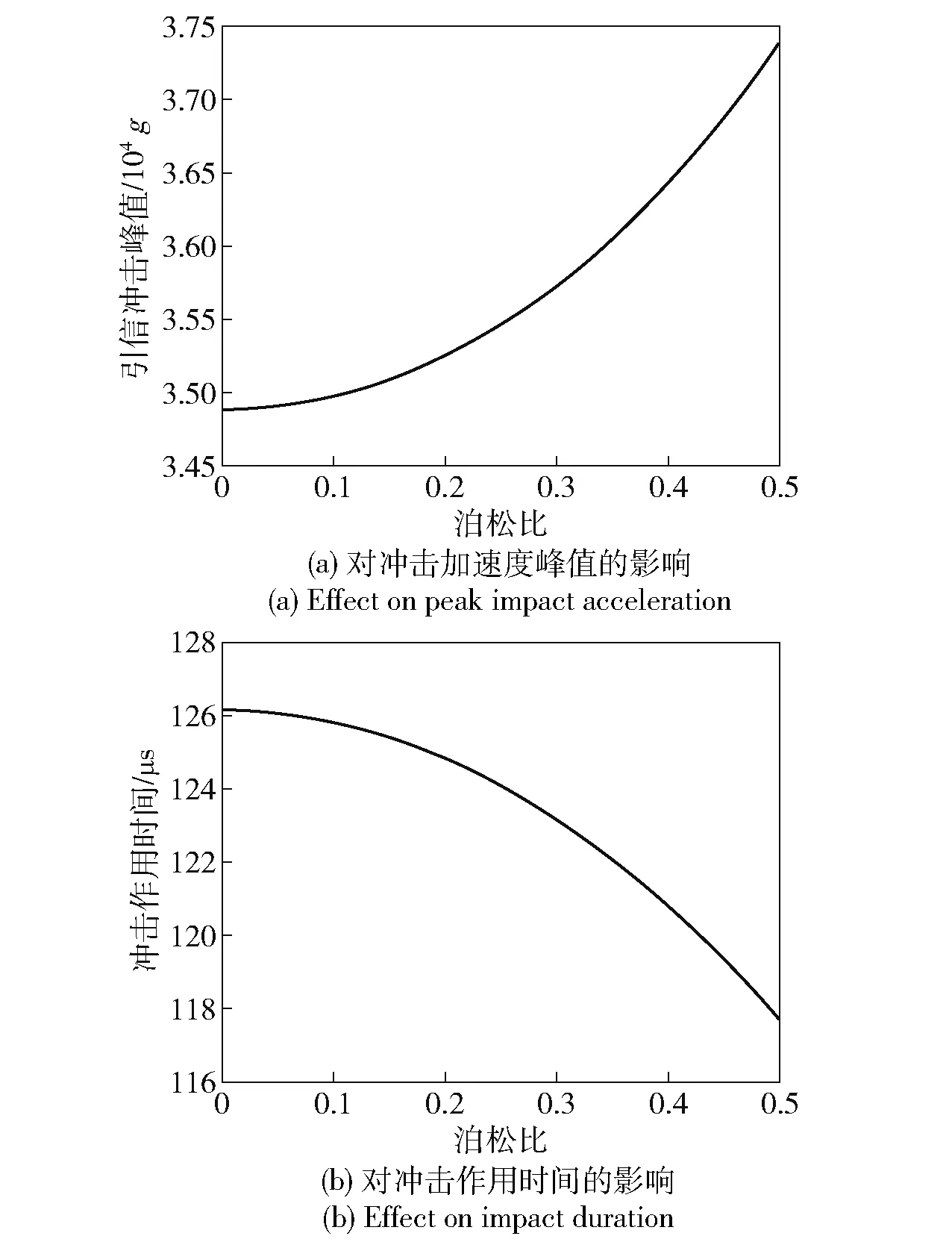
圖6 地面目標泊松比對引信沖擊特性的影響Fig.6 Effect of poisson's ratio of ground target on impact characteristics of fuze

改變地面目標的彈性模量,采用計算公式求得彈丸以1.5 m 落高跌落不同地面目標時引信沖擊加速度峰值與作用時間變化,如圖7 所示。由圖7 可見,地面目標的彈性模量對引信沖擊特性影響程度巨大,彈性量越大,彈丸跌落時產生引信的沖擊加速度峰值越大,沖擊時間越短。

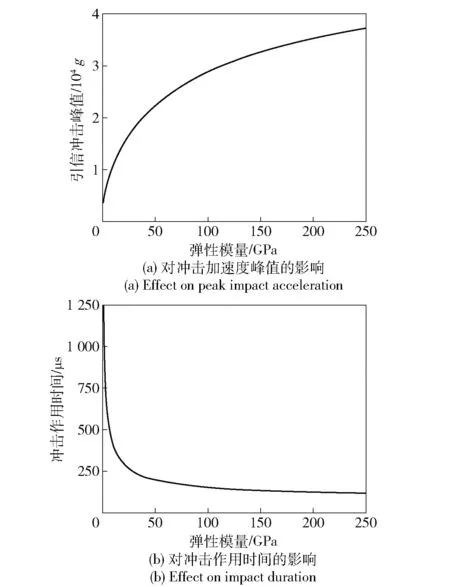
圖7 地面目標彈性模量對引信沖擊特性的影響Fig.7 Effect of ground target elastic modulus on impact characteristics of fuze

從(27)式和(29)式的形式可以看出,彈體材料與地面目標材料的影響程度是相同的,因此上述規律對彈體材料同樣適用。

通過計算公式與仿真表明,彈丸直徑影響跌落時的引信沖擊特性,彈丸直徑越大,跌落時產生的沖擊峰值越小,沖擊作用時間越長;彈丸直徑越小,沖擊峰值越大,沖擊時間越短;彈丸跌落碰撞地面目標時,跌落高度僅改變沖擊加速度峰值大小,跌落高度越高,引信沖擊加速度峰值越大;碰撞恢復系數僅改變沖擊作用時間的長短,二者的碰撞恢復系數越大,碰撞時間越短。

(30)式為引信沖擊加速度峰值與沖擊作用時間計算公式的乘積,該公式較為簡潔。

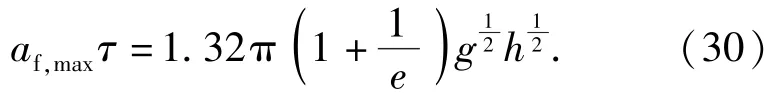
假設彈丸跌落碰撞地面目標過程為完全彈性碰撞,則=1,進而(30)式可進一步化簡為

即二者的乘積僅與跌落高度有關,即在完全彈性碰撞的情況下,彈丸以同一高度跌落至任意目標,沖擊加速度峰值與沖擊作用時間乘積是恒定不變的。

3 算例驗證

文獻[6]給出了100 mm 口徑平底榴彈底向下以不同落高垂直跌落鋼板的引信沖擊加速度和沖擊時間仿真數據。文獻[15]將不同口徑的試驗彈從1.5 m 高度以底向下姿態自由跌落到鋼板上,通過安裝在引信部位的傳感器測量并記錄每種試驗彈丸引信部位的沖擊加速度信號。利用本文得到的計算公式分別計算文獻[6]中100 mm 口徑彈丸與文獻[15]中3 種不同口徑平底彈丸(76 mm 彈、85 mm彈和122 mm 彈)的引信沖擊加速度峰值和沖擊作用時間,對比結果如表14 和表15 所示。

表14 計算公式與仿真結果對比Tab.14 Comparison of calculated and simulated results

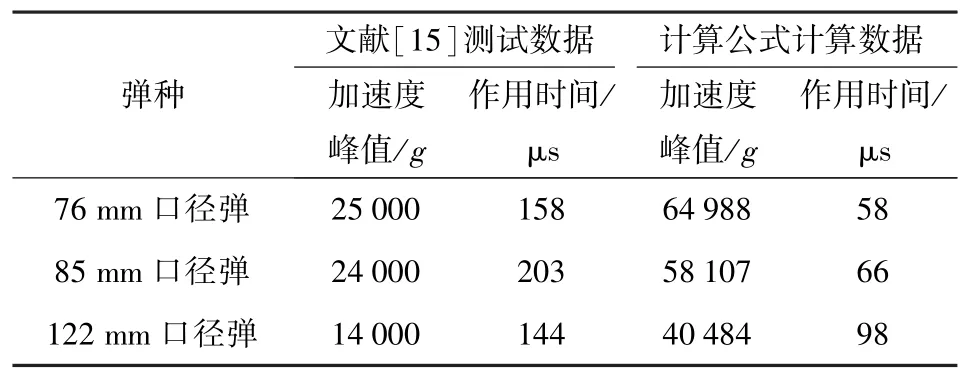
表15 計算公式與測試結果對比Tab.15 Comparison of calculated and test results

由表14 和表15 可以看出,(27)式和(29)式的計算結果與仿真結果相近,誤差在可接受范圍內;計算加速度峰值偏大于測試數據,而作用時間結果偏小于測試數據。文獻[6]仿真結果表明,彈丸由垂直跌落到1°傾角,沖擊峰值迅速減小。對文獻[6]所給出35 mm、100 mm、130 mm 3 種不同口徑榴彈跌落仿真數據進行處理,利用MATLAB 軟件擬合得到引信跌落沖擊峰值相對衰減量隨傾斜角度變化趨勢圖,如圖8 所示,相應的函數表達式可近似表示為

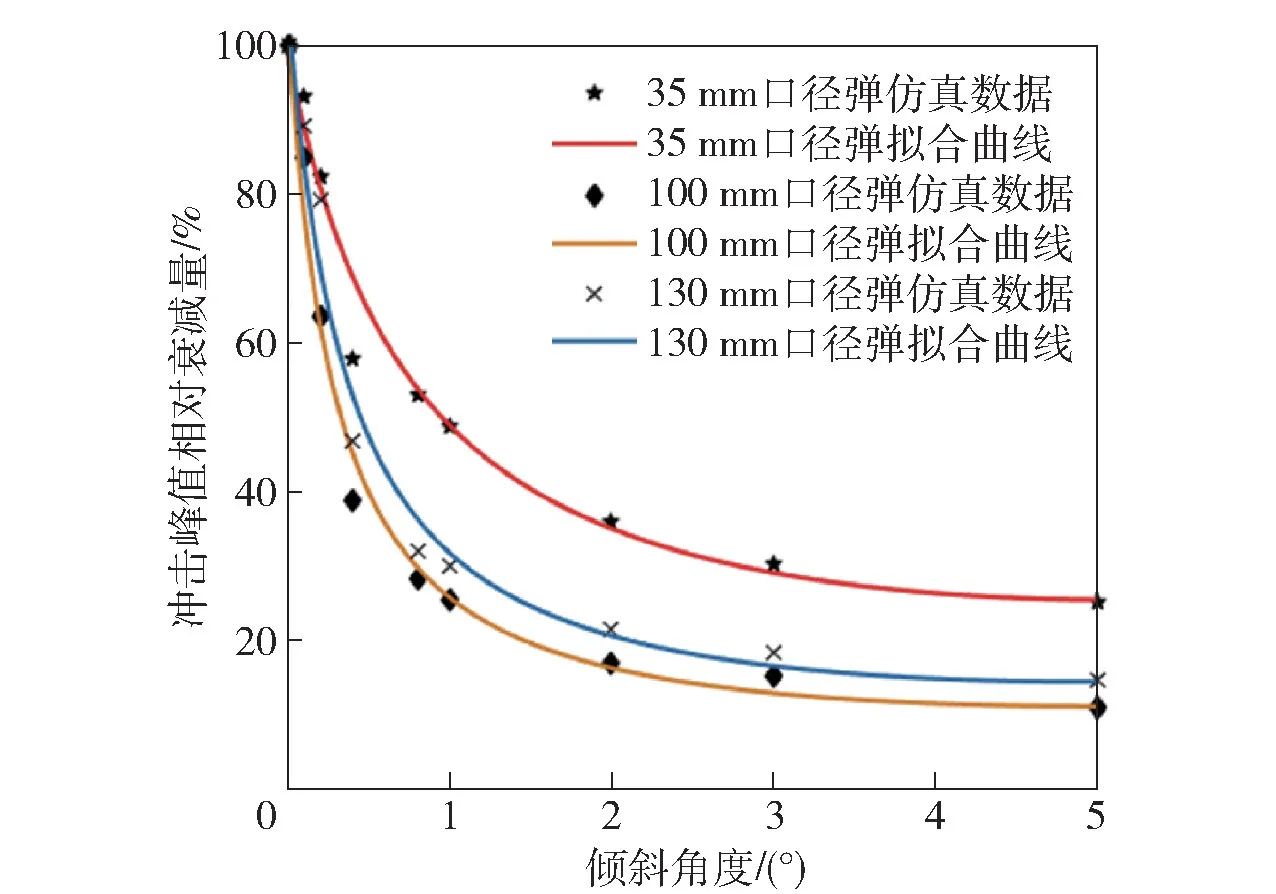
圖8 引信跌落沖擊峰值相對衰減量隨傾斜角度的變化趨勢Fig.8 Changing trend of relative attenuation of fuze drop impact peak with inclination angle

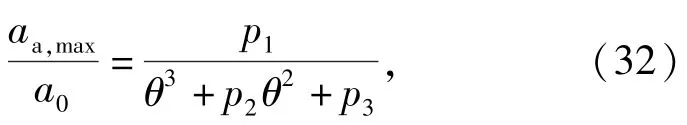
式中:為不同角度跌落下引信跌落沖擊峰值;為垂直跌落時引信跌落沖擊峰值;為彈丸傾斜角度;、、均為常系數。

6 種不同口徑彈丸以不同角度從1.5 m 高度跌落至鋼板,其彈丸跌落沖擊加速度峰值仿真結果如表16 所示。彈丸傾斜角度對跌落沖擊峰值影響是巨大的,考慮到傳統自由落體式跌落試驗彈丸跌落姿態接近“隨機”,且樣本量很少,實際測試結果難以出現完全垂直跌落的極端情況,因而所得加速度峰值會系統變小而作用時間會系統變長,故由此可認為本文推導的彈丸跌落產生的沖擊加速度峰值和沖擊作用時間計算公式具有較高的可信性。

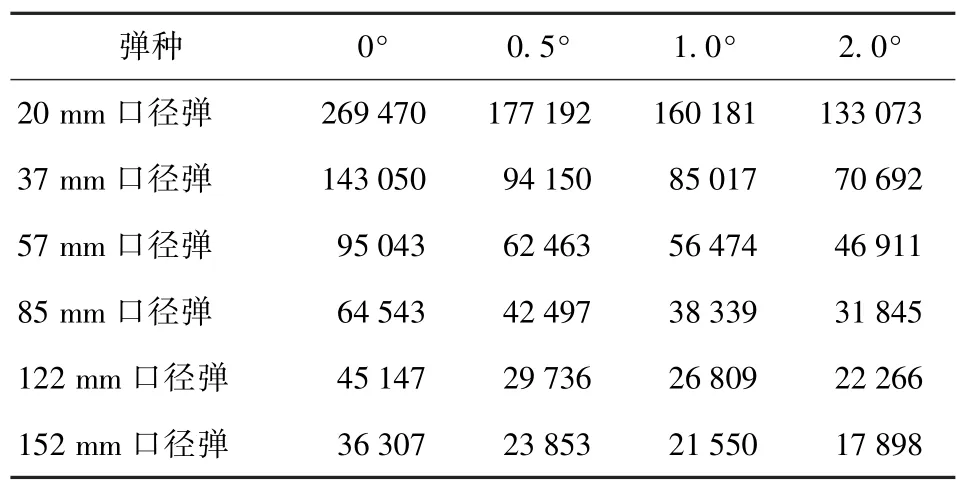
表16 不同口徑彈丸以不同角度從1.5 m 高度跌落于鋼板時的彈丸沖擊加速度峰值Tab.16 Peak impact acceleration of projectiles with different calibers dropping on steel targets from 1.5 m height at different angles g

4 結論

本文采用彈塑性力學理論推導出了底部為圓柱形的彈丸垂直跌落碰撞地面目標過程的沖擊加速度峰值和作用時間理論計算公式;利用有限元軟件對不同口徑縮比彈丸進行了跌落數值仿真,對沖擊加速度峰值和作用時間的仿真結果進行了常系數修正,得到了裸態平底榴彈彈丸底向下垂直跌落時彈丸和引信的沖擊特性公式。得到主要結論如下:

1) 彈丸直徑越大,跌落時產生的沖擊峰值越小,沖擊作用時間越長;跌落高度僅改變沖擊加速度峰值大小;碰撞恢復系數僅改變沖擊作用時間的長短。

2) 在完全彈性碰撞的情況下,彈丸以同一高度跌落至任意目標,沖擊加速度峰值與沖擊作用時間乘積是恒定不變的。