基于灰關聯分析和時空偏好特征的興趣點推薦算法

陳江美, 張文德

(1. 福州大學經濟與管理學院, 福建 福州 350108; 2. 福州大學信息管理研究所, 福建 福州 350108)

0 引 言

隨著移動社交網絡的普及與應用,多樣化的位置簽到及共享功能不斷涌現,獲取用戶的地理信息更為容易,助推了基于位置的社交網絡(location-based social network,LBSN)的興起。例如,目前較為流行的Gowalla、Yelp、Foursquare等移動平臺不僅具備社交功能,還為用戶提供了諸多與位置有關的服務。LBSN中主要包含了用戶與位置屬性、社交關系及簽到時間等信息,用戶可通過“簽到”的方式分享其可能喜歡的地點,從而衍生出多樣化的位置服務功能。其中,興趣點(point-of-interest,POI)推薦作為一項重要的服務內容,近年來受到了學者的廣泛關注。POI是指用戶簽到的地點,如景點、電影院等,興趣點推薦能夠有效緩解位置過載問題,從而提升用戶在LBSN中的個性化體驗,并有助于商家挖掘潛在客戶,成為了當前研究的熱點問題。

目前,國內外學者對 POI推薦工作已開展大量的研究,并設計不同的推薦策略來改善推薦性能,但仍存在一些局限。首先,用戶的偏好存在漂移性,即用戶的興趣可能隨時間在動態變化,雖然少數研究將時間納入POI推薦工作,但性能有待提高。LBSN中的用戶簽到矩陣十分稀疏,而當前納入時間的研究主要是利用時間間隙來劃分矩陣,加劇了評分矩陣的數據稀疏性。因此,如何合理地挖掘用戶的時間偏好是重點。其次,用戶的移動行為符合個性化特征,但多數的研究認為用戶的地理行為偏向于統一的分布,未充分考慮用戶個性化特征,如何更好地實現地理行為的個性化值得研究。最后,LBSN存在海量的異構數據,這些異構數據對推薦結果有著不同程度的影響,如何有效地融合多類型異構數據增加了推薦的難度。

在傳統POI推薦工作的基礎上,本文針對上述問題,提出了一種基于灰關聯分析和時空偏好(grey relational analysis and temporal-spatial information, GRA-TS)的POI推薦算法。本文的貢獻主要有以下3點:

(1) 考慮用戶偏好動態變化和數據稀疏性問題,提出將時間融入矩陣分解算法中,以刻畫用戶對POI的時間偏好。同時,將灰色系統理論沿用于此,利用灰關聯分析方法度量各時間段的相似度,從而減弱數據稀疏的影響,有效改善推薦性能。

(2) 考慮用戶的簽到分布符合個性化特征,采用自適應核密度估計方法來模擬用戶的空間偏好,從而捕捉用戶的空間偏好。

(3) 綜合考慮用戶的時間偏好和空間偏好特征,通過模擬用戶的時空偏好行為,獲得用戶的綜合偏好分數。同時,將本文提出的算法進行數據實驗,結果表明了該算法相較于其他基準算法具有更優的推薦性能。

1 研究綜述

基于位置的社交網絡中蘊含著豐富的信息,目前POI推薦的相關研究主要通過融合上下文信息(如地理信息、時間信息),采用協同過濾算法、矩陣分解算法、深度學習、譜聚類等方法模擬用戶的決策行為。在已有的研究中,考慮用戶對地理距離較敏感的特性,Ye等人采用冪律分布建模用戶的地理行為偏好,將地理信息融入基于用戶的協同過濾算法中。但交互矩陣十分稀疏,協同過濾方法難以發揮作用。考慮矩陣分解算法能緩解稀疏問題,文獻[6-7]將地理信息納入加權矩陣分解算法的框架中以挖掘用戶的偏好。Zhang等人則考慮用戶潛在的地理和社交信息,通過矩陣分解算法聯合求解用戶的綜合偏好。為了進一步挖掘用戶的地理行為偏好,文獻[9-11]將地理因素結合多種情景信息來模擬用戶的簽到行為,進而提高推薦質量。

近年來,一些學者在試圖改善推薦性能時,將用戶簽到的時間作為重要的情景信息融入推薦工作中。為了模擬用戶的時間偏好,學者們從多個角度進行建模。Yin等人利用協同過濾技術為目標用戶在給定時間推薦地點。但協同過濾技術易受稀疏影響,推薦效果不佳。Gao等人將時間所具有的非統一性和連續性嵌入矩陣分解算法中。但由于考慮要素單一,無法全面挖掘用戶的偏好。Rahmani等人考慮用戶的周期性行為,將時空信息納入矩陣分解框架中。文獻[15]融合空間、社交和時間信息的影響,探究各要素在POI推薦工作中的作用。上述算法雖考慮了時間影響,但主要利用時間劃分簽到矩陣,造成原本就稀疏的矩陣更加稀疏,導致動態推薦效果不佳。

綜上可知,目前大量的基于時空的研究成果仍存在局限性。傳統動態推薦的工作鮮少考慮時間特征的影響,造成對用戶的時間偏好挖掘不充分,同時忽略了時間戳細化用戶簽到矩陣后帶來的稀疏性影響。另外,上述的工作主要將用戶的地理行為建模為統一的距離分布,忽略了用戶的個性化行為。為此,本文提出了一種新的基于時空偏好的POI算法,以提高用戶的動態個性化推薦效果。

2 灰關聯分析方法

灰色系統理論是一種能處理貧信息問題的方法。灰關聯分析是灰色系統理論中一種重要的研究方法,通過判斷序列曲線幾何形狀的相近程度以衡量序列間的相似性,對樣本數據量及數據的分布規律無特殊要求,可有效處理復雜貧信息系統的數據。因此,本文將灰關聯分析理論運用到推薦系統領域中,用來度量數據稀疏條件下的相似度。

2.1 灰關聯度

灰關聯系數:設={()|∈}為參考序列,={()|∈}為對應的比較序列,={1,2,…,},={1, 2,…,},稱

((),())=

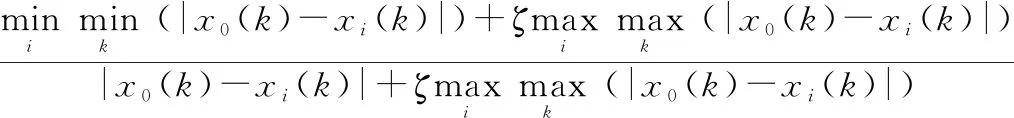
(1)

為參考序列和比較序列在處的灰關聯系數。其中,為分辨系數,一般取05。

灰關聯度:設存在((),())為非負數,為度量參考序列和比較序列的相似度,稱

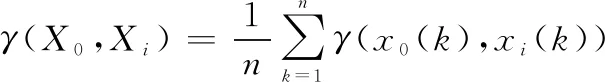
(2)

為第個比較序列的灰關聯度。

2.2 灰關聯熵與熵關聯度

灰關聯密度:由定義1可知,((),())為參考序列和比較序列在處的灰關聯系數,稱

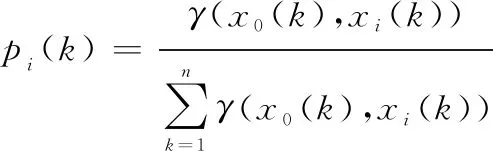
(3)

為第個比較序列在處的灰關聯密度。

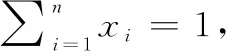
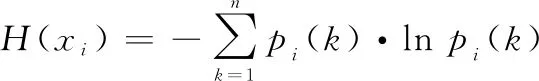
(4)

為第個比較序列的灰關聯熵。

熵關聯度:設表示第個比較序列的灰關聯系數,稱

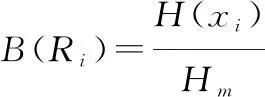
(5)

為第個比較序列的熵關聯度。其中，=ln,表示最大熵。

2.3 均衡接近度

傳統的灰關聯分析方法存在局部異常點的傾向及信息損失的局限,為了克服此缺陷,在灰關聯分析方法中引入灰關聯熵,利用均衡接近度作為衡量向量之間相似度的標準。

均衡接近度:由灰關聯度和熵關聯度組合乘積,得

(,)=(,)·()

(6)

式中：(,)表示參考序列和比較序列的均衡接近度。

均衡接近度方法由傳統的灰關聯分析方法發展而來,灰色系統理論中灰關聯度的概念可用于描述向量間的相似性。近年來,相關學者將灰關聯分析方法拓展到推薦領域。文獻[25]指出傳統的相似性度量方法面臨數據稀疏性和相關性兩大挑戰,結合灰關聯分析方法提出一種新的協同過濾預測模型。文獻[26-27]利用灰關聯分析挖掘數據的關聯性,進而探索用戶間的關系。文獻[28]將灰色系統理論應用到社交推薦中,通過優化預測模型,以緩解數據稀疏性和差異性。本文沿用這一思路,將灰色系統理論引入POI推薦領域,并將均衡接近度的概念用到時間相似度之上,以改進傳統的余弦相似度方法存在局部異常點的不足,進而提高相似度計算的準確性,改善數據稀疏問題。

3 GRA-TS推薦算法

3.1 算法框架及思想

本文從時間和空間的角度出發,設計出統一的POI推薦算法框架,如圖1所示。本算法主要思想是將用戶簽到的時間特征細化,分解帶有時間戳的用戶評分矩陣,利用處理小樣本的灰關聯分析方法度量時間相似度,進而降低稀疏性的影響。同時,運用自適應核密度估計方法個性化地建模用戶的空間偏好。最終,提出了一種GRA-TS算法,在第32～第34節將給出詳細的模型描述。

圖1 GRA-TS算法的框架結構圖

3.2 引入時間特征的矩陣分解算法

與協同過濾算法建模時間偏好相比,矩陣分解算法具有更好的可擴展性與緩解稀疏性的能力。鑒于用戶的簽到行為受時間影響,本節將時間的個性化和連續性特征融入矩陣分解算法框架中,結合灰關聯分析方法,以描述用戶對POI的時間偏好。

321 時間個性化特征建模

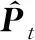
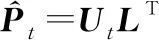
(7)

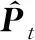
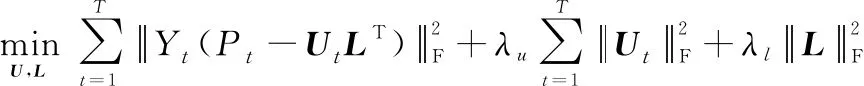
(8)

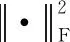
322 時間連續性特征建模

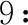
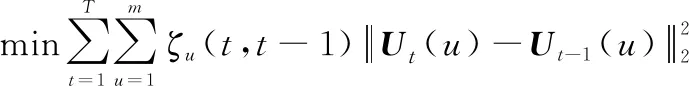
(9)

式中：(,-1)表示時間段和-1的相似度;()表示用戶在時間間隔內的簽到偏好。為了簡化損失函數,當=1時,令=-1,則-1=,將其轉化為矩陣形式如下:

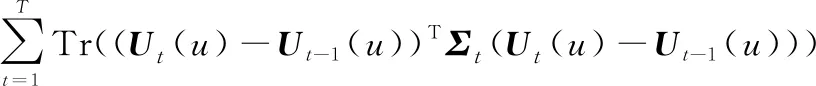
(10)

式中：表示個用戶間的對角時間系數矩陣,表達式如下:

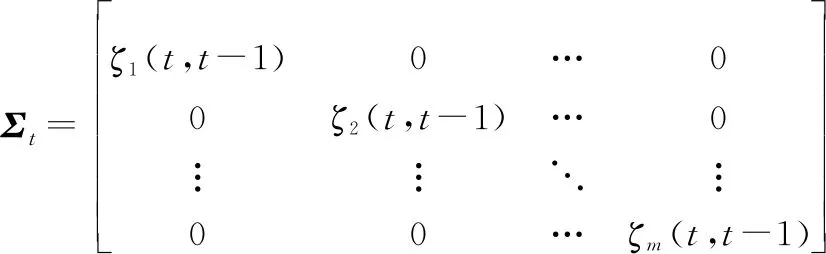
(11)

323 灰關聯分析度量相似度

灰關聯分析方法可用于衡量向量間的關聯程度,借助灰色理論中“接近度”的思想,利用均衡接近度方法計算用戶簽到POI各時間段間的相似度。因此,利用式(6)均衡接近度方法對式(9)中的時間相似度進行求解如下:

(,-1)=(,-1)

(12)

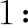
324 統一的時間偏好特征

本節綜合考慮上述時間個性化和連續性特征,并建立統一的時間偏好函數。由于式(8)和式(10)中的同為用戶特征偏好矩陣,若單獨對兩個優化函數求解很難滿足統一性要求。鑒于此,本節將兩個矩陣分解的優化函數聯合求解如下:

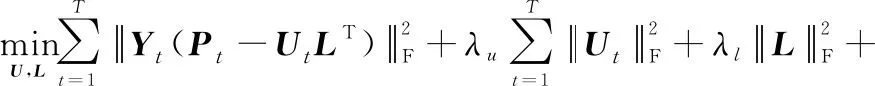
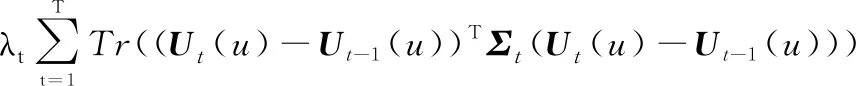
(13)

式中:為調整時間正則化的參數。

本文利用變更最小二乘法(alternative least square, ALS)對目標函數進行優化,當求解一個隱特征向量時,固定其他變量。其中矩陣和為待求解參數,訓練過程中其更新公式如下:

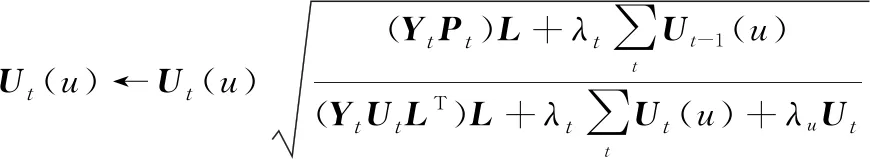
(14)

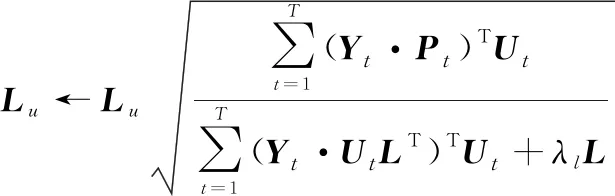
(15)

通過優化式(14)和式(15),可求解參數矩陣和,并將其代入式(7)計算得到預測矩陣中的各元素值, 將其定義為用戶的時間偏好特征預測值。

3.3 引入空間信息的個性化推薦算法

用戶的空間偏好通常指用戶的決策受地理位置信息的影響程度,考慮地理位置對用戶的簽到行為具有重要作用,本文利用自適應核密度估計方法來建模用戶的空間偏好,以實現個性化推薦。設={,,…,}表示用戶已簽到POI集合,其中∈,(,)表示POI的經緯度坐標。同時,考慮用戶的空間偏好特征,利用核密度估計方法捕捉用戶的地理偏好,并將高斯分布作為核函數,獲得用戶對未簽到POI的預測函數為

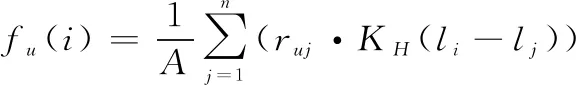
(16)

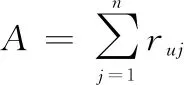
(17)

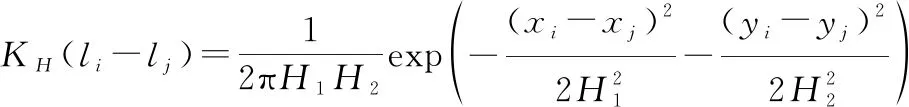
(18)

式中:表示用戶簽到POI的總次數;表示用戶對POI的訪問次數;(-)表示包含兩個全局固定帶寬(,)的核函數。(,)的公式如下:

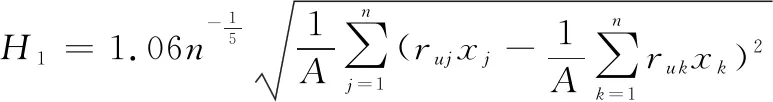
(19)

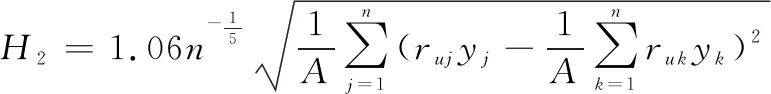
(20)

為實現個性化推薦,本文并非直接利用式(16)的()值來描述用戶的空間偏好,而是用來決策每個被簽到POI的自適應帶寬:

=(())-

(21)

式中:表示敏感參數,值越大意味著對()越敏感;表示幾何平均數,的表達式如下:

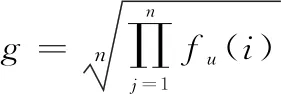
(22)

最終,根據式(19)和式(20)的固定帶寬值(,)和式(21)的自適應帶寬值,預測用戶在未簽到POI上的自適應核估計的推薦概率分布如下:

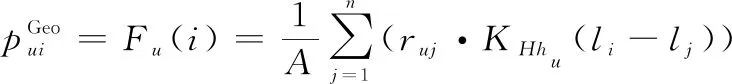
(23)

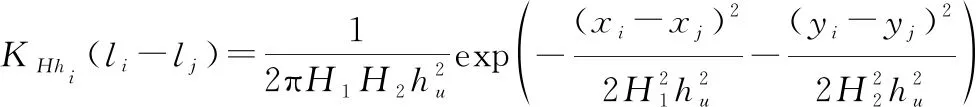
(24)

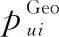
3.4 融合時空特征的算法優化

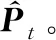
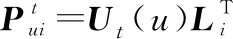
(25)

因此,將式(25)與式(23)中度量用戶的空間偏好的算法相結合,建立最終的統一優化算法GRA-TS,獲得用戶未簽到POI的最終預測偏好如下:

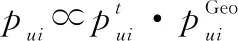
(26)

4 數據實驗與分析

4.1 數據集介紹

本文實驗的數據集來自Foursquare網站,該網站是一個基于用戶地理位置的社交網站,采用其發布的真實公開的Foursquare數據集來評估所提算法的性能,其包含的具體內容如表1所示。

表1 數據集統計

為了評估算法的精度,先進行數據預處理,過濾掉一些發生次數較少的異常數據,分別刪除訪問頻率少于10個POI的用戶和被訪問頻率少于10個用戶的POI。

4.2 度量指標

為了驗證本文算法的有效性,將實驗中用戶簽到數據按8∶2的比例隨機分成訓練集和測試集。根據top-的推薦排序,為每個用戶推薦得分最高的前個POI,并對生成的POI推薦列表進行評估。本文主要是對算法的基本性能作對比,重點是找出通過訓練算法生成的POI列表總數中有多少是目標用戶在測試集中實際簽到的POI。準確率precision@與召回率recall@是top-推薦中的兩個基本指標。為此,在對比實驗部分采用這兩個基本指標進行算法的評估,公式如下:

(27)

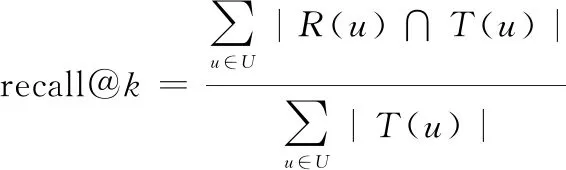
(28)

式中:()表示訓練集通過本文算法訓練生成的POI推薦列表;()表示測試集中用戶對POI的簽到列表。

4.3 實驗對比與算法評估

為了評估算法的性能,選取了5種基準算法與本文提出的GRA-TS算法進行比較。

(1) LRT算法:基于時間效應的POI推薦算法,考慮時間非統一性和連續性兩大特征,將其分別納入矩陣分解算法,綜合求解獲得用戶的最終偏好。

(2) SCGT算法：融合社交、分類、地理與時間信息的POI推薦算法利用固定帶寬的核密度估計捕捉用戶的地理偏好,并結合社交信息提出統一的推薦模型。

(3) iGSLR：融合地理與社交影響的位置推薦算法，采用固定帶寬的核密度估計方法模擬用戶的地理行為,利用協同過濾建模用戶的社會影響力,通過融合獲得最終的用戶偏好。

(4) PRUG：基于用戶興趣和地理因素的POI推薦算法，利用自適應核密度估計與樸素貝葉斯算法捕捉用戶的空間偏好,結合用戶的偏好生成統一的模型。

(5) STACP：基于時空偏好的POI推薦算法，考慮用戶簽到行為的周期性,利用矩陣分解框架建模時空信息的影響,求解獲得用戶的潛在偏好。

其中,LRT與STACP是兩種基于時間因素的算法,可有效地研究動態推薦的效果。而SCGT、iGSLR、PRUG及STACP分別采用了不同的地理建模方式來挖掘用戶的偏好,有利于充分探究個性化推薦問題。同時,這些算法結合了一種或多種情景信息,有助于研究時空信息對推薦工作的影響,進而驗證本文算法的有效性。因此,將上述5種算法作為本文的對比方法。

在實驗的參數設置部分,依據文獻[13]中的最優參數的選取,將本文算法中的正則化參數、和分別設置為2,2,1,經過實驗測試適用于本文的算法,并應用于以下實驗。對敏感參數,通常將值取為0.5,經驗證此時用戶的地理偏好得分最佳。

4.3.1 相似度優化對推薦性能影響

為了探究灰關聯分析方法度量時間相似度對推薦結果的影響,本節將基于GRA的時間影響模型(GRA-temporal, GRAT)算法與基準算法LRT進行對比。其中,GRAT是本文算法的一部分,主要利用矩陣分解算法描述時間的個性化和連續性特征,與LRT相比,GRAT算法采用均衡接近度方法刻畫時間段間的相關性,而非運用傳統的余弦相似度度量方法。

本實驗選取為5、8、10、12、15和20,分別對比兩種算法在Foursquare數據集上的推薦精度和召回率的變化情況,并將實驗中的參數設為最優值。從圖2(a)和圖2(b)看出,GRA算法的推薦準確率和召回率相較于LRT有顯著的提高,表明了均衡接近度方法在度量時間相似度方面較余弦相似度方法具有更突出的效果,說明了本文相似度優化的有效性。灰關聯分析方法能改善推薦性能的原因歸結兩點:① 傳統的相似度方法易遭受局部異常點影響,造成數據損失而影響推薦質量,而均衡接近度方法可以減弱局部異常點的影響;② 均衡接近度方法能處理貧信息問題,本算法利用時間劃分矩陣造成了嚴重的稀疏問題,將灰關聯分析方法沿用于此,并采用矩陣分解算法能有效改善數據稀疏性。因此,實驗結果表明了利用均衡接近度來計算相似度能改善推薦性能。

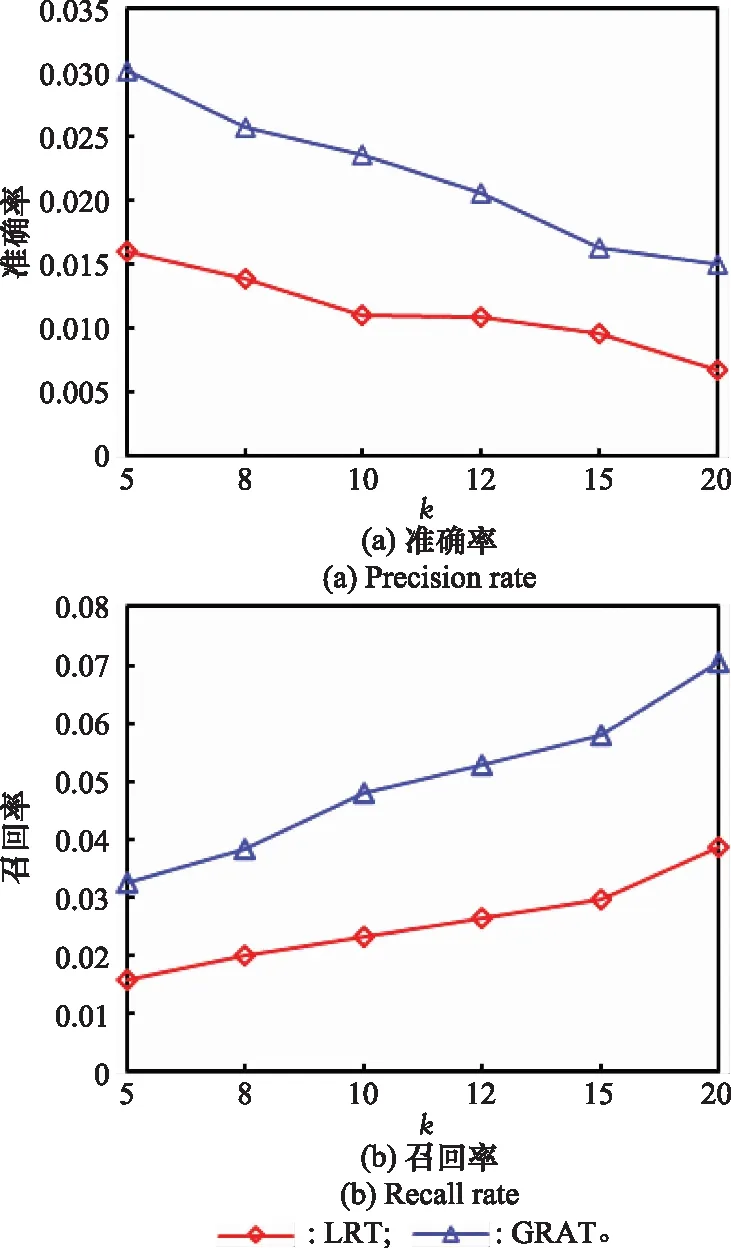
圖2 相似度優化前后的推薦準確率和召回率

4.3.2 地理因素影響

為了研究基于冪律分布的地理因素在預測用戶偏好上的影響,同時探究采用自適應核密度估計方法捕捉用戶地理偏好的有效性,將本文提出的GRA-TS算法與GRAT算法、基于灰關聯分析與冪律分布(grey relational analysis-power law distribution, GRAP)的算法進行對比。其中,GRAT算法是本文算法的一部分,與GRA-TS算法相比,此算法未考慮地理因素的影響。GRAP則利用冪律分布來模擬地理行為影響。實驗比較為5、8、10、12、15和20時,3種算法在數據集上的準確率和召回率變化情況,如圖3所示。

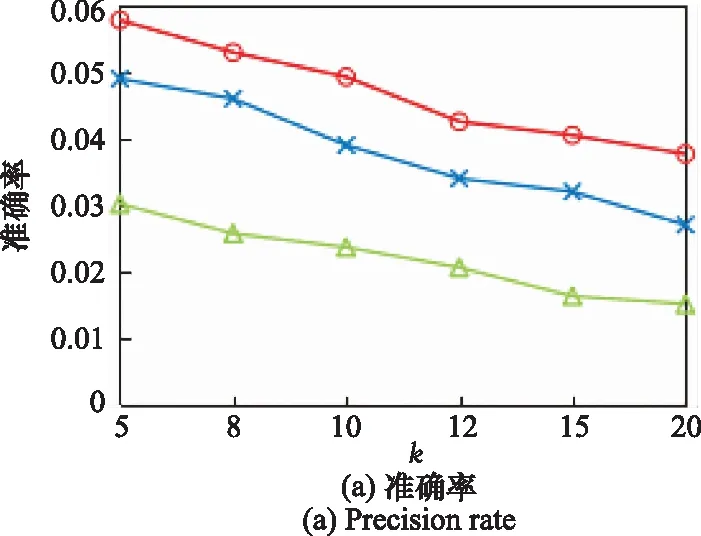
圖3 融合不同地理信息的算法性能對比

由圖3看出,未考慮地理因素的GRAT算法的推薦準確率和召回率低于其他兩種算法,說明地理信息在本文的推薦工作中具有重要意義,是影響推薦策略的主要因素之一。GRAP算法與本文所提的算法相比,顯然看出GRA-TS算法的推薦性能更優。GRAP利用冪律分布捕捉用戶的地理偏好,性能優于GRAT算法,但其將用戶的移動行為視作統一的分布,忽視了用戶個性化行為的影響。GRA-TS算法利用自適應核密度估計方法描述用戶個性化的簽到行為,表現出最好的推薦性能,說明了本文對地理建模的合理性。

4.3.3 算法的性能對比與分析

在Foursquare數據集的基礎上,將本文算法的參數設定為=2、=2和=1時推薦性能最佳,并根據其他5種文獻設置的參數值,使各算法的推薦效果最優。實驗將6種算法進行比較,對比結果如圖4所示,其描述了各算法在POI推薦列表長度為5、8、10、12、15和20時的推薦性能。從圖4看出,本文提出的GRA-TS算法的性能最優。同時,值的增加有易于用戶挖掘更多的POI,因此各算法的推薦準確率在逐漸降低與召回率在逐漸升高。由圖4(a)和圖4(b)可見,GRA-TS算法的推薦準確率和召回率在相同條件下均優于其他5種算法,特別相較于LRT的性能有顯著提升。考慮LRT只納入時間信息,且算法遭受嚴重的數據稀疏問題,因此推薦的性能最低。SCGT與iGSLR采用固定帶寬的核密度估計函數建模地理影響,并融合社會影響力,初步考慮了不同用戶的地理行為偏好,但兩種算法易受到數據稀疏影響。STPACP將用戶的時空偏好嵌入矩陣分解框架,與SCGT與iGSLR相比,矩陣分解分解算法能緩解稀疏問題,但未充分挖掘用戶簽到的時間特征,性能有待提高。PRUG融合了核密度估計和樸素貝葉斯算法描述用戶的地理偏好,結合了用戶偏好影響,性能優于上述4種算法,但未考慮用戶的動態偏好,結果次優。與上述5種算法對比,本文提出的GRA-TS算法考慮了時間的個性化和連續性特征,進而描述用戶的時間偏好,并運用灰關聯分析度量時間相關性,緩解了數據稀疏的影響,提高了動態推薦效果。同時,利用自適應核密度估計方法捕捉用戶的移動行為偏好,有效地實現個性化推薦,增強了推薦的時空特征關聯。綜上,GRA-TS算法的推薦性能最佳,表現出最好的推薦性能。

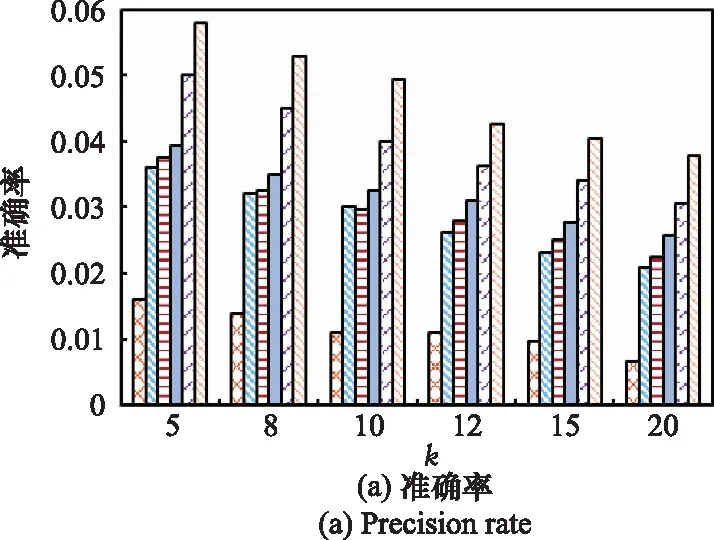
圖4 6種算法在Foursquare上的推薦性能

5 結 論

為了提高動態推薦與個性化推薦的效果,本文提出了一種基于GRA-TS的POI推薦算法。該算法將用戶簽到的時間特征細化,把灰關聯分析與矩陣分解算法相結合,利用灰關聯分析計算時間相似度,減少了數據稀疏的影響,有效地提高了動態推薦的效果,為應對推薦系統的稀疏性問題提供了新的方法。還采用了自適應核密度估計建模用戶的地理行為,增強了個性化體驗。實驗結果表明,本文提出的算法在推薦準確率和召回率方面均優于其他基準的推薦算法。在未來的工作中,將進一步挖掘更多的情景信息來提高推薦性能。同時,將異地問題作為突破重點,進一步深入完善模型。