基于AEKF的高速自旋飛行體組合導(dǎo)航方法

董一平, 劉 寧,*, 蘇 中, 王靖驍, 白宏陽

(1. 北京信息科技大學(xué)自動化學(xué)院, 北京 100192; 2. 北京信息科技大學(xué)高動態(tài)導(dǎo)航技術(shù)北京市重點(diǎn)實(shí)驗(yàn)室, 北京 100192; 3. 南京理工大學(xué)能源與動力工程學(xué)院, 南京 210094)

0 引 言

現(xiàn)代軍事中,精確化打擊已經(jīng)成為主要的發(fā)展方向。高速自旋飛行體在飛行過程中自身高速旋轉(zhuǎn)產(chǎn)生陀螺力矩,能夠克服由推力偏心、質(zhì)量偏心、氣動偏心等引起的誤差,具有較強(qiáng)的抗干擾能力。因此,受到世界上各軍事強(qiáng)國的普遍重視。高速自旋是一種繞自身軸線的旋轉(zhuǎn)速度為10 rev/s (1 rev=360°)以上的運(yùn)動狀態(tài),廣泛使用于航天、武器、民用等領(lǐng)域中。高速自旋飛行體主要包括:火箭彈類、導(dǎo)彈、彈箭類等,同時(shí)具有較高的打擊能力,在增雨防雹、太空探索等民用領(lǐng)域也發(fā)揮重大作用,因此研究高速自旋飛行體的制導(dǎo)問題至關(guān)重要。

高速自旋飛行體在制導(dǎo)過程中,需要實(shí)時(shí)對飛行體的位置坐標(biāo)、飛行姿態(tài)、飛行速度等參數(shù)進(jìn)行解算,但存在著一定的困難。文獻(xiàn)[9]中給出火箭彈的滾動角度較大,衛(wèi)星在捕捉信號時(shí)難度較大;文獻(xiàn)[10]中指出火箭彈飛行過程中橫滾角過大,需要較大的動態(tài)測量范圍,對陀螺儀的精度要求較高。高速自旋飛行體的滾轉(zhuǎn)角速度可達(dá)上百轉(zhuǎn)每秒,單純使用捷聯(lián)慣導(dǎo)系統(tǒng)(strapdown inertial navigation system,SINS),則陀螺儀具有較大的測量范圍,但其分辨率會減低,導(dǎo)致測量誤差增大。

針對上述問題,組合導(dǎo)航的方式可以將SINS與北斗衛(wèi)星導(dǎo)航系統(tǒng)二者互補(bǔ),同時(shí)具有精度高,抗干擾能力強(qiáng)等優(yōu)點(diǎn),更好發(fā)揮優(yōu)勢。文獻(xiàn)[13]提出了全球定位系統(tǒng)(global positioning system, GPS)/慣性測量單元(inertial measurement unit, IMU)組合方式,采用擴(kuò)展卡爾曼濾波方法(extended Kalman filter, EKF)進(jìn)行濾波;文獻(xiàn)[9]給出了INS/GPS超緊耦合的組合導(dǎo)航方法。但超緊組合方式對信息限制較多,使用不便捷;文獻(xiàn)[14]給出了采用地磁輔助的微機(jī)械(micro electro mechanical system,MEMS)陀螺進(jìn)行火箭彈姿態(tài)測量;文獻(xiàn)[15]提出了基于MEMS的IMU和北斗衛(wèi)星組合的方式,并通過無跡卡爾曼濾波算法對據(jù)進(jìn)行融合,提高彈道參數(shù)測量的精度。

組合導(dǎo)航的濾波方式有多種,主要為卡爾曼濾波(Kalman filter, KF)算法和以其為基礎(chǔ)的改進(jìn)算法。EKF作為估計(jì)工具,在控制領(lǐng)域具有一定地位,但在非線系統(tǒng),EKF可能出現(xiàn)偏差。傳統(tǒng)的EKF算法,其系統(tǒng)噪聲協(xié)方差矩陣和量測噪聲協(xié)方差矩陣設(shè)定為常值,但實(shí)際系統(tǒng)噪聲是隨機(jī)的,所以濾波誤差會增大。因此,本文基于自適應(yīng)EKF(adaptive EKF, AEKF)算法進(jìn)行數(shù)據(jù)融合,對量測噪聲進(jìn)行估計(jì),改進(jìn)AEKF算法。

本文基于北斗/SINS松組合模型,使用改進(jìn)的AEKF算法對數(shù)據(jù)進(jìn)行融合,根據(jù)北斗衛(wèi)星是否更新判斷進(jìn)入量測。仿真結(jié)果表明,與未改進(jìn)的相比,改進(jìn)的AEKF算法系統(tǒng)濾波誤差更小,系統(tǒng)更加穩(wěn)定,同時(shí)具有輕量級的優(yōu)點(diǎn)。

1 AEKF算法

1.1 AEKF算法實(shí)現(xiàn)

AEKF算法是在EKF算法的基礎(chǔ)上演變而來,增加了遺忘因子,以對系統(tǒng)的噪聲進(jìn)行估計(jì),達(dá)到減小誤差的效果。EKF算法是解決非線性狀態(tài)估計(jì)最為直接且性能較好的方法。由于噪聲的不可知性,對EKF的算法造成影響。AEKF既有EKF適用于非線性系統(tǒng)的優(yōu)點(diǎn),又能夠?qū)ξ粗脑肼曔M(jìn)行估計(jì),進(jìn)而適應(yīng)不斷變化的噪聲情況。因此,向EKF中引入自適應(yīng)機(jī)制。

使用較為廣泛的AEKF算法為Sage-Husa算法,該算法主要通過觀測數(shù)據(jù)進(jìn)行濾波的同時(shí),使用噪聲統(tǒng)計(jì)估計(jì)器,能夠?qū)崟r(shí)地估計(jì)和修正系統(tǒng)的系統(tǒng)噪聲和量測噪聲,具體引入帶遺忘因子的噪聲統(tǒng)計(jì)估計(jì)值。

設(shè)線性離散化系統(tǒng)方程和量測方程分別為

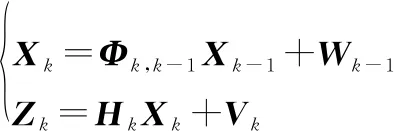
(1)

式中：是系統(tǒng)時(shí)刻的維估計(jì)狀態(tài);是系統(tǒng)時(shí)刻的維觀測序列;是系統(tǒng)狀態(tài)轉(zhuǎn)移矩陣;是觀測矩陣;-1,分別是系統(tǒng)噪聲和量測噪聲序列,相互獨(dú)立且為正態(tài)白噪聲。則Sage-Husa算法具體描述為

狀態(tài)預(yù)測:

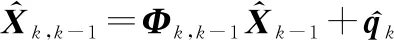
(2)

(3)

殘差:

(4)

量測更新:

(5)

式中:為時(shí)刻EKF的增益矩陣。

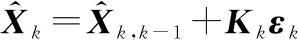
(6)

=[-],-1

(7)

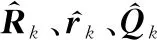
自適應(yīng)估計(jì)器為

(8)

(9)

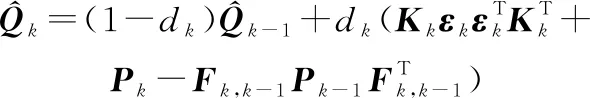
(10)

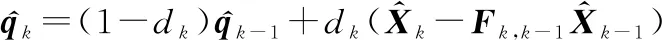
(11)

式中：=(1-)(1-+1)(0<<1)為遺忘因子,其作用為加強(qiáng)新數(shù)據(jù)對濾波的作用。

1.2 算法改進(jìn)

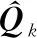
本文在此基礎(chǔ)上,對自適應(yīng)器的量測噪聲估計(jì)公式中添加系數(shù),其中添加系數(shù)的目的是更準(zhǔn)確地反映量測噪聲的變化情況,具體為

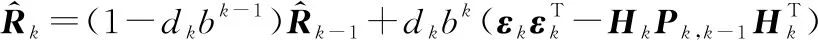
(12)

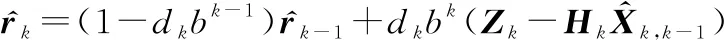
(13)

2 組合導(dǎo)航系統(tǒng)

2.1 坐標(biāo)系選取

本文采用SINS,使用導(dǎo)航坐標(biāo)系北-東-地坐標(biāo)系;組合導(dǎo)航系統(tǒng)借助衛(wèi)星信號修正,衛(wèi)星信號為WGS-84國際統(tǒng)一的大地坐標(biāo)系經(jīng)度、緯度和高度。為統(tǒng)一計(jì)算,將衛(wèi)星信號從大地坐標(biāo)系轉(zhuǎn)換至中間地心直角坐標(biāo)系,再轉(zhuǎn)換至北-東-地(N-E-D)坐標(biāo)系。

2.2 數(shù)學(xué)模型

傳統(tǒng)的EKF建模方法,對于建模所需的變量易于選取,但在計(jì)算過程中需要每次對非線性數(shù)據(jù)采用雅各比矩陣的方式進(jìn)行線性化,計(jì)算量大,對實(shí)時(shí)性有較大影響。因此本文采用對系統(tǒng)方程和量測方程的非線性函數(shù)作泰勒級數(shù)展開并僅保留線性項(xiàng),獲得線性模型,提高系統(tǒng)的實(shí)時(shí)性。

選取系統(tǒng)的誤差量作為狀態(tài)變量:位置誤差Δ、速度誤差Δ、姿態(tài)誤差Δ、加速度計(jì)零偏誤差Δ和陀螺零偏誤差Δ,建立狀態(tài)方程如下:

(14)

(15)

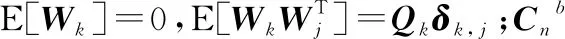
(16)

其次,建立量測方程+1=[+1,+1],具體如下式所示:

(17)

2.3 系統(tǒng)實(shí)現(xiàn)

本次組合導(dǎo)航系統(tǒng)采用松組合的方式,具有易實(shí)現(xiàn)和有冗余度的優(yōu)點(diǎn)。SINS隨時(shí)間增加造成誤差積累,北斗衛(wèi)星導(dǎo)航系統(tǒng)具有全天候、實(shí)時(shí)性高等優(yōu)點(diǎn),與SINS組合使用,二者能夠互補(bǔ)。結(jié)構(gòu)框圖如圖1所示。

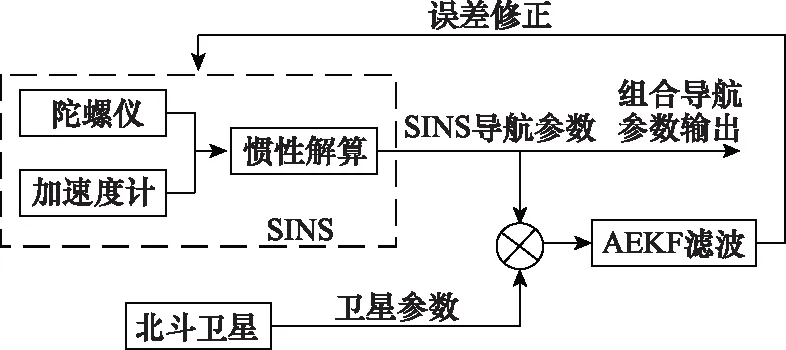
圖1 組合導(dǎo)航系統(tǒng)組成

首先需要對系統(tǒng)進(jìn)行初始對準(zhǔn),是獲取的高準(zhǔn)確性和高實(shí)時(shí)性是高精度組合導(dǎo)航實(shí)現(xiàn)的前提。初始對準(zhǔn)目的是獲取載體的速度、位置和姿態(tài)信息。然后對SINS數(shù)據(jù)進(jìn)行解算,得到飛行體的位置、速度和姿態(tài)信息,并把獲取的北斗衛(wèi)星數(shù)據(jù)進(jìn)行坐標(biāo)變換。由于SINS更新速度快于北斗衛(wèi)星數(shù)據(jù),需要判斷北斗衛(wèi)星是否進(jìn)入量測更新,以保證修正數(shù)據(jù)的準(zhǔn)確性。在更新時(shí),用北斗衛(wèi)星數(shù)據(jù)校正SINS數(shù)據(jù),使用AEKF算法,對量測噪聲進(jìn)行估計(jì);在非量測更新階段,單獨(dú)采用SINS對飛行體進(jìn)行定位。

具體硬件系統(tǒng)包括慣性測量模塊、彈載計(jì)算機(jī)模塊和數(shù)據(jù)記錄模塊。慣性測量模塊包括陀螺儀、三軸加速度計(jì);彈載計(jì)算機(jī)采用Cortex-M7+FPGA的架構(gòu)進(jìn)行設(shè)計(jì);數(shù)據(jù)記錄儀用于數(shù)據(jù)存儲。具體硬件實(shí)物如圖2所示。

圖2 硬件實(shí)物圖

3 仿真分析

為驗(yàn)證本次改進(jìn)算法在高速自旋飛行體上的可行性,利用Matlab軟件對實(shí)際載體運(yùn)動的數(shù)據(jù)進(jìn)行仿真分析。

載體運(yùn)動軌跡為拋物線,實(shí)地觀測結(jié)果為飛行高度約為2 000 m,飛行距離約為15 000 m,飛行總時(shí)長為46.5 s,發(fā)射角為25°。SINS的更新速率為1 ms,北斗衛(wèi)星的更新速率為100 ms。仿真參數(shù)的誤差描述如表1所示。實(shí)際陀螺儀和加速度計(jì)的測量數(shù)據(jù)如圖3和圖4所示。

表1 仿真參數(shù)誤差

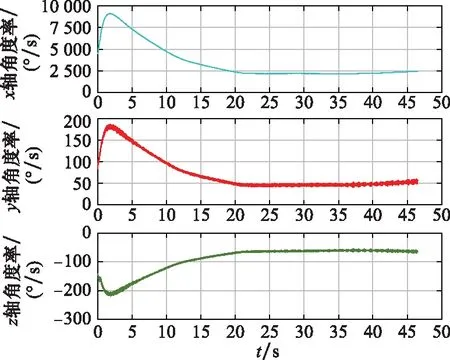
圖3 陀螺儀測量數(shù)據(jù)

圖4 加速度計(jì)測量數(shù)據(jù)

本文采用組合導(dǎo)航,使用AEKF濾波方法對SINS和北斗的數(shù)據(jù)進(jìn)行融合,對比未改進(jìn)與改進(jìn)的AEKF算法對濾波誤差的影響。

3.1 AEKF算法對量測噪聲估計(jì)

本文經(jīng)過分析,采用AEKF算法對量測噪聲協(xié)方差矩陣進(jìn)行估計(jì)。組合導(dǎo)航軌跡東向-地向平面信息、位置誤差和速度誤差如圖5～圖7所示。遺忘因子取0.9。

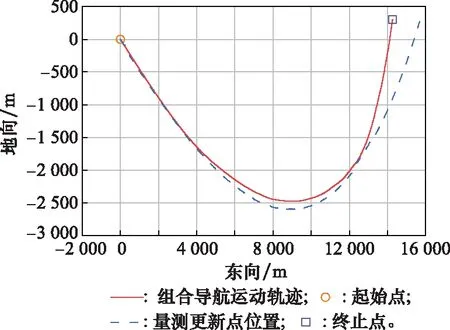
圖5 組合導(dǎo)航軌跡東向-地向平面信息

圖6 算法改進(jìn)前的位置誤差

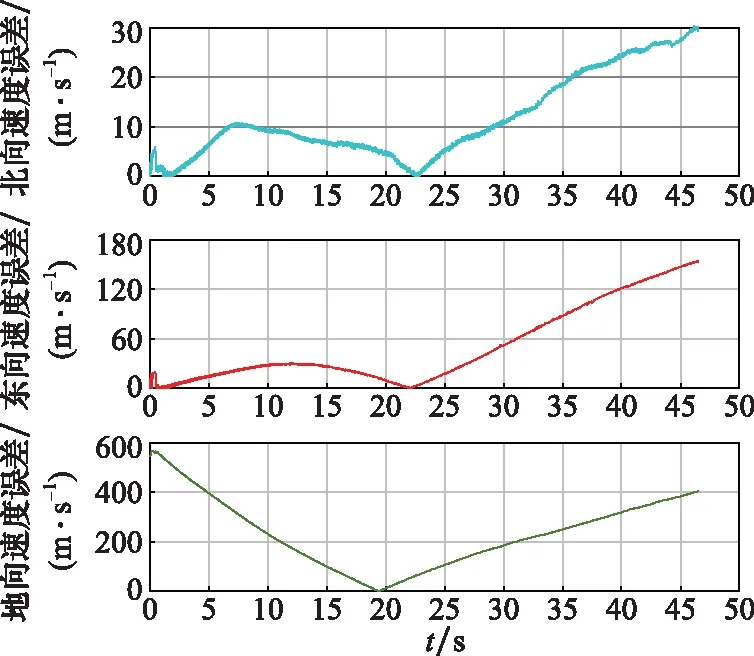
圖7 算法改進(jìn)前的速度誤差

由圖5可以看出,SINS信息沒有被修正過來,在后期誤差越來越大,與北斗的觀測數(shù)據(jù)有一定偏差。從圖6和圖7也可以看出,誤差越來越大,沒有趨于穩(wěn)定。位置誤差在30 s時(shí)開始不斷上升,地方向上最后下降,整體偏高;速度誤差在20 s時(shí)整體上升。因此,以上方法的濾波效果不佳。

3.2 改進(jìn)的AEKF算法

由上一組為改進(jìn)的AEKF算法仿真結(jié)果可知,組合導(dǎo)航濾波出現(xiàn)明顯偏差,結(jié)束點(diǎn)的位置與北斗的量測位置相距1 400 m。因此,采用改進(jìn)的AEKF算法進(jìn)行濾波。位置誤差、速度誤差如圖8和圖9所示。遺忘因子取0.9。

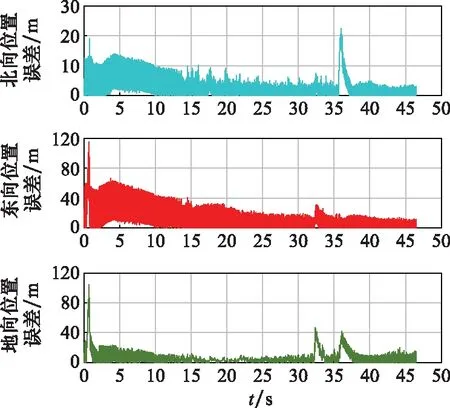
圖8 b=0.9時(shí)的位置誤差

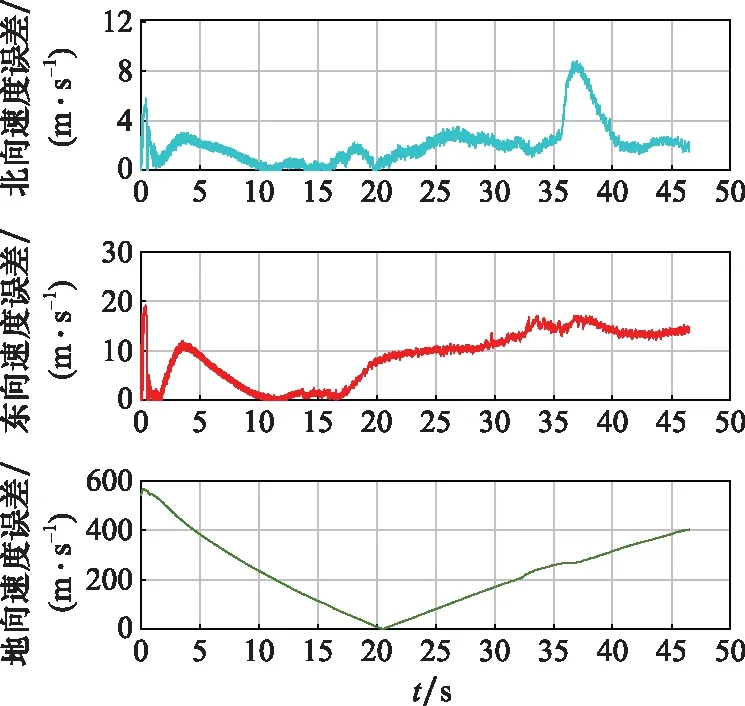
圖9 b=0.9時(shí)的速度誤差

由圖8可以看出,位置誤差漸趨平穩(wěn),且均收斂,雖然在35 s時(shí),有次波動,但很快調(diào)節(jié),恢復(fù)收斂,與未改進(jìn)AEKF算法對比明顯,且誤差大范圍下降,最后北向位置誤差保持在3 m 范圍內(nèi),東向誤差平均保持在6 m 范圍內(nèi)。由圖9可知,速度誤差也有較大改善,在北向、東向兩方向上分別收斂于2 m/s 和14 m/s,效果明顯。地向速度改動不明顯。

再次調(diào)節(jié)遺忘因子,改善系統(tǒng)濾波能力。經(jīng)過反復(fù)調(diào)試,取遺忘因子為0.3,得到位置、速度誤差如圖10和圖11所示。

圖10 b=0.3時(shí)的位置誤差

圖11 b=0.3時(shí)的速度誤差

經(jīng)過調(diào)節(jié)遺忘因子參數(shù),由圖11可知,速度誤差進(jìn)一步改善,東向誤差再次下調(diào)位置誤差改變不明顯,但位置、速度誤差保持穩(wěn)定。經(jīng)過此次濾波算法調(diào)節(jié),組合導(dǎo)航運(yùn)動軌跡如圖12所示。

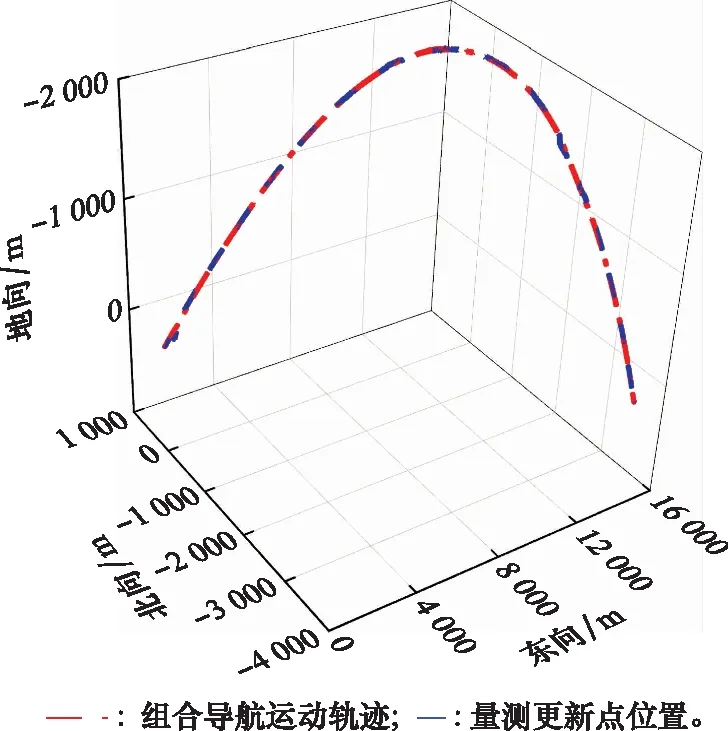
圖12 組合導(dǎo)航運(yùn)動軌跡圖

組合導(dǎo)航軌跡表明,濾波算法有效,將SINS數(shù)據(jù)在量測更新階段校正過來,避免誤差干擾,與圖5對比,有明顯改善。組合導(dǎo)航軌跡跟隨北斗量測的數(shù)據(jù)進(jìn)行調(diào)整。由上述未改進(jìn)AEKF算法與不同參數(shù)調(diào)整的改進(jìn)AEKF算法,可以得出,位置誤差由發(fā)散,最終北向位置誤差為 2 m,東向位置誤差為6 m,地向位置誤差7 m。北向、東向速度誤差從發(fā)散調(diào)整為收斂,最終北向速度誤差為2 m/s 范圍內(nèi),東向速度誤差為 10 m/s。由此表明,本文改進(jìn)的AEKF濾波算法行之有效,能夠保證組合導(dǎo)航濾波的穩(wěn)定性。

4 結(jié) 論

本文研究了基于AEKF算法的高速自旋飛行體組合導(dǎo)航方法,針對EKF算法中系統(tǒng)存在的噪聲問題,引入了自適應(yīng)器,添加遺忘因子對量測噪聲進(jìn)行估計(jì),并對EKF的建模做了調(diào)整,每次計(jì)算過程中不必重復(fù)計(jì)算雅可比矩陣,提高系統(tǒng)的實(shí)時(shí)性,采用濾波算法控制,對高速自旋飛行體的組合導(dǎo)航控制中具有輕量級的優(yōu)點(diǎn)。通過AEKF算法與改進(jìn)的AEKF算法對比,改進(jìn)的算法能夠明顯降低誤差,并保證誤差漸趨穩(wěn)定,進(jìn)入收斂。通過本次仿真,得到AEKF算法能夠提高導(dǎo)航精度,但還能夠進(jìn)一步改善,后續(xù)工作繼續(xù)調(diào)整算法,并且采用其他算法進(jìn)行修正,如無跡卡爾曼算法等。本文僅對系統(tǒng)的量測噪聲進(jìn)行修正,能夠自適應(yīng)估計(jì)協(xié)方差矩陣,保證了北斗/SINS組合導(dǎo)航的定位精度,并且提高系統(tǒng)的穩(wěn)定性。