基于低軌星網的多目標協同跟蹤濾波技術

翟 光, 王妍欣, 孫一勇

(北京理工大學宇航學院, 北京 100081)

0 引 言

星網探測系統將天基觀測器和光學傳感器相結合,以其覆蓋范圍廣、精度高、傳感距離遠而受到廣泛的關注。與單顆衛星相比,星網能夠整合整個衛星星座采集的數據,實現目標的連續跟蹤[1-2]。由于衛星探測范圍內可能存在多個目標以及光學傳感器的各種不確定性,因此根據量測值無法直接反推目標的位置[3]。一旦將錯誤的測量值分配給目標,會對估計結果產生巨大影響。當目標進行機動時,目標的動力學模型隨即改變,增加了多目標協同跟蹤的難度。因此,研究一種針對低軌星網的多目標跟蹤算法具有重要意義。

基于低軌星網的多目標的跟蹤問題可以分為數據關聯階段和多目標狀態更新階段。數據關聯技術是狀態估計問題的前提,在多目標協同跟蹤中起著重要作用[4]。多目標數據關聯技術旨在建立目標與量測值之間的映射關系,并實現對量測值的分配。最近鄰數據關聯(nearest neighbor data association, NNDA)算法是最著名的數據關聯算法之一,其通過比較目標預測位置和測量值之間的距離來區分目標的相關測量和雜波干擾。除了最近鄰思想,還有一種基于概率分析的數據關聯思想,如概率數據關聯(probabilistic data association, PDA)[5]解決了雜波背景下簡單目標的數據關聯問題。在PDA算法的激勵下,相關學者又提出了聯合PDA(joint PDA, JPDA)[6]和多假設跟蹤(multiple hypothesis tracking, MHT)[7]實現多目標的數據關聯。JPDA算法考慮了多個量測來源于其他目標可能性,但算法所需的計算量呈指數級增長[8]。MHT算法被證明是一種適用于多目標跟蹤的貝葉斯最優算法,但其精確解的計算存在困難[9]。為了減少計算量,又開發了廉價JPDA(cheap JPDA, CJPDA)[10]、次優JPDA (suboptimal JPDA, SJPDA)[11]和多幀分配(multiple frame assignment, MFA)[12]算法。然而,大部分數據關聯算法都是根據對目標的三維量測信息進行關聯,根據光學傳感器平面的二維量測信息即目標的方位角進行多目標數據關聯的算法很少。由于任意兩個不關聯的角度軌跡都可能產生幻影目標,因此必須確定測量值的來源,將來源于同一目標的量測值進行關聯。為解決這一問題,文獻[13]提出最小距離偏差算法,文獻[14]提出二面傾角算法。然而這些算法都利用了幾何約束,無法實現時間維度上的數據關聯。因此,有必要開發一種數據關聯算法,從空間和時間兩個維度解決數據關聯問題。

狀態更新階段即是根據測量值的關聯結果估計多個目標的狀態。卡爾曼濾波(Kalman filter, KF)是一種應用最廣泛的狀態估計算法[15]。雖然KF已被證明在高斯白噪聲假設下能獲得線性離散系統在方差最小意義下的最優估計[16],但由于低軌星網和目標的動態特性,KF不適用于多目標跟蹤。為了將KF擴展到非線性系統中,學者們進行了大量的研究。在現有的非線性濾波器中,擴展KF(extended KF, EKF)因其實現簡單、計算量小而得到廣泛應用,由于EKF采用二階泰勒展開對非線性系統進行近似,忽略了高階項,因此只適用于弱非線性系統。為了更精確地逼近非線性系統,文獻[17-18]采用基于無跡變換的無跡KF(unscented KF, UKF)來解決多目標跟蹤問題。綜合考慮對非線性系統的逼近精度和計算量之間的平衡,本文采用基于UKF的狀態更新方法。然而,目標的機動序列對跟蹤系統未知會使得濾波器的性能顯著下降[19-20]。一般來說,由目標機動引起的濾波發散問題可以通過膨脹協方差以增加新測量值權重的方法解決[20-21]。但這種方法只適用于脈沖式機動。文獻[22-23]提出了一種基于協方差膨脹的衰減記憶濾波器來解決機動目標跟蹤(maneuvering target tracking, MTT)問題。這兩種算法的思想都是增加測量值的權重,但其代價是跟蹤精度的降低。文獻[24-25]通過將未知機動增廣到估計狀態,提出了增廣KF(augmented KF, AFK)。但由于狀態維度的增加帶來了更大的計算量。為解決這個問題,學者們提出了變結構濾波算法[26],利用KF和AKF,既能保持機動目標的跟蹤精度,又能提供較好的非機動目標跟蹤性能。在變結構方法的推動下,多種算法得到發展,如變狀態維度(variable state dimension, VSD)算法[27],增強VSD(enhanced VSD, EVSD)算法[28]等。與單濾波器相比,交互式多模型算法[29-30]則是對多個單獨模型跟蹤的估計值進行加權求和,得到組合狀態估計,但同時運行多個濾波器必然增加了計算量,特別是對于非機動目標,不僅不會提高跟蹤性能,反而會降低定位精度。

本文針對低軌星網只能獲得目標方位角信息的測量特性,通過設計指標函數來確定測量值的分配,將三維關聯轉化為測量平面關聯,有效地實現多目標的數據關聯;并將狀態更新與數據關聯算法相結合,建立了多機動目標跟蹤算法的總體框架。通過機動檢測函數確定機動的開始和結束,從而完成狀態估計器在標準UKF和增廣UKF(augmented UKF, AUKF)之間的切換。最后通過仿真試驗對算法的可行性與有效性進行驗證。

1 數學模型

1.1 目標彈道動力學模型

導彈離開大氣層后,進入自由飛行段,在不考慮空氣動力學和地球自轉的情況下,目標運動僅受到重力和發動機推力的影響。考慮帶有推進器的多個目標,取目標j(j=1,2,…,Nt)在地心慣性坐標系下的位置[x,y,z]T和速度[vx,vy,vz]T為狀態向量,即

X(j)=[x,y,z,vx,vy,vz]T,j=1,2,…,Nt

(1)

式中:Nt為t時刻目標總個數。多目標在地心慣性坐標系下的動力學模型可以描述為

(2)

式中:μ0=3.986×105km3/s2為地心引力常數;W(j)(t)表示目標的系統噪聲,其方差陣為Q(j)。

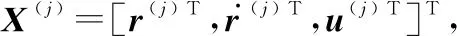
1.2 彈道目標天基觀測模型

低軌星網的衛星以一定的構型在空間分布,其中Walker星座是一種常用的圓形軌道星座,星座內衛星的軌道具有相同的高度、傾角和偏心率,其星座構型可用N/P/f描述,其中N為衛星總個數,P為衛星分布的軌道面數,f為相鄰軌道面衛星相對相位因子。設星座中某顆衛星編號為m,則衛星m的升交點赤經和近地點角距可以表示為

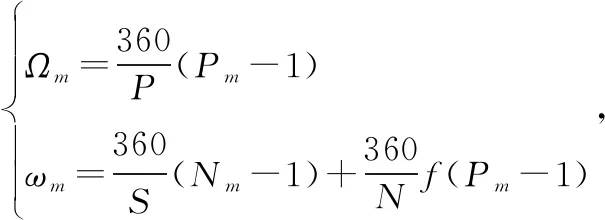
(3)

對于配備光學傳感器的衛星,當目標進入衛星的探測范圍,如圖1所示,就可以獲取目標的方位角信息。對于目標j,若滿足如下條件則可被衛星i探測到:

(4)

式中:α(i)表示衛星i的半視場角;η(ij)表示衛星i和目標j之間的夾角;ST表示由衛星至目標的位置矢量;OS表示地心至衛星位置矢量。根據余弦定理,式(4)可以寫為

(5)

(6)

式中:[xs,ys,zs]T表示衛星在地心慣性坐標系中的位置向量。

若衛星和目標滿足式(5)和式(6),則表示目標處于衛星的探測范圍。對于攜帶光學傳感器的衛星,可以得到目標在星固坐標系下的方位角和俯仰角,根據目標j和衛星i在地心慣性坐標系中的狀態矢量,可以得到目標在地心慣性坐標系下的量測方程:

(7)

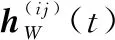
從量測方程中也可以看出,量測值中包含衛星的位置信息,因此利用量測信息得到的目標狀態估計值必然與衛星自身定軌精度相關。為了在低軌星網的觀測條件下實現多目標的協同跟蹤,除了衛星星座的定軌精度,還必須保證各衛星時間基準和空間基準的統一,只有在統一時空架構下獲取的觀測信息才能用于多目標的數據關聯及狀態更新。因此,本文提出如下假設。

(1) 衛星配備完善的自主導航體系,能夠滿足在星座構型保持及重構過程中的自主定位。因此在本文中認為衛星的導航精度很高,衛星自身的導航誤差不足以影響對目標的跟蹤精度。

(2) 用于多目標跟蹤的低軌星座經過準確的時空對準,且網絡傳輸無延遲,即用于協同跟蹤的量測值都是同一時刻獲得的,且無延遲地傳送到處理中心。

2 多目標協同跟蹤濾波

2.1 基于卡方分布的數據關聯

本文的目的是設計一種針對低軌星網的多目標協同跟蹤濾波算法。由于根據單顆衛星獲得的目標方位角無法反推目標的三維位置信息,使得針對三維軌跡的數據關聯算法失效。實現對多目標的狀態估計的前提是明確不同量測值的來源,即量測值的數據關聯。低軌星網的多星對多目標觀測關系隨時間變化情況如圖2所示。從圖2中可以看出,要實現多目標的協同跟蹤,一方面需要根據量測的來源將當前時刻的量測進行分組;另一方面,需要建立當前被檢測目標與歷史目標之間的映射,以繪制完整的軌跡。

(8)

定義一個目標被一顆衛星觀測到一次為一組量測,則星座對多目標的量測組數為

(9)

為了根據這Ntrk組量測得到多目標的三維軌跡,對NNDA算法進行改進,利用變結構框架實現多目標的數據關聯和狀態估計。

由于光學傳感器只能得到目標的方位角信息,本文構建虛擬的量測跟蹤門,并利用卡方分布對量測數據進行分配,以實現測量平面的數據關聯。基于卡方分布的數據關聯算法主要包括如下步驟。

(10)

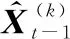
(11)

(12)

式中:h為選定的時間步長。

進一步得到狀態的一步預測值為

(13)

(14)

(15)

(16)

(17)

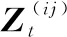
(18)

式中:Assi表示衛星i觀測到的量測與已有目標的數據關聯結果。

2.2 信息融合與多目標狀態更新

由第2.1節設計的數據關聯指標函數可以實現量測量的分配,進而可以通過KF算法對多星的測量結果進行數據融合從而實現多目標狀態更新。但是由于目標機動存在不確定性,若不考慮目標機動會導致目標狀態方程的不準確,進而導致濾波精度降低。AKF被廣泛用于未知機動推力恒定的目標狀態估計。然而,由于AKF增加了系統狀態,其實時性不如標準KF。本文跟蹤的目標是彈道導彈的自由飛行段,目標受力特性較為簡單,僅受重力和發動機推力的影響,不需要考慮空氣動力,因此目標機動的原因只有發動機的推力,可以較為準確地建立以目標動力學模型為基礎的狀態方程。針對標準KF和AKF的切換問題,提出了變結構估計(variable structure estimation, VSE)。在VSE的激勵下,本文開發了一種可變結構UKF(variable structure UKF, VSUKF)來自適應地估計未知機動。在VSUKF框架內,如果檢測到機動,濾波器結構將切換為AUKF,即

(19)

當機動結束時,則利用UKF估計目標的狀態,即

(20)

為了根據量測分配矩陣得到目標的量測矩陣,定義如下算法函數:

C=Meas(A,B)

(21)

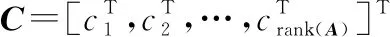
cj=aA(i)bA(i),i=1,2,…,n;j=1,2,…,rank(A)

(22)

式中:A(i)=diag(a1,a2,…,ai)為矩陣A的分塊矩陣;A(i)=rank(A(i))為矩陣A(i)的秩。

由此,目標k的量測矩陣可以表示為

(23)

式中:I1×2=[1,1]表示1×2維的矩陣，且矩陣元素全部為1。

與量測值對應的衛星位置矩陣可以表示為

(24)

根據數據關聯的結果,目標k的狀態估計值為

(25)

(26)

(27)

計算量測值采樣點:

(28)

(29)

計算濾波增益矩陣:

(30)

將式(23)和式(30)代入式(25)可以得到

(31)

均方誤差陣更新:

(32)

(33)

(34)

(35)

(36)

2.3 變結構框架下的機動信息估計

對于機動目標,在機動開始或結束時準確地改變濾波器結構是目標狀態準確估計的前提。但由于無法準確得知目標的機動序列,通過設置機動探測器以準確探測機動的開始和結束。在目標機動初始階段,雖然濾波器的估計協方差幾乎保持不變,但其測量殘差會增加,因此根據測量殘差對機動的靈敏度,構造如下機動開始檢測器:

(37)

(38)

若滿足:

(39)

類似地,構造如下機動終止檢測器：

(40)

(41)

與交互多模型算法相比,變結構濾波框架不需要同時運行多個濾波器,而是通過機動檢測器判斷機動的開始和結束,從而實現不同濾波器之間的切換,計算量較少,適用于本文中目標的受力場景。對于機動目標,濾波器在目標機動時切換為AUKF,可以對目標的位置、速度和機動加速度信息進行估計,在目標非機動時則采用UKF;對于非機動目標,則一直采用UKF進行狀態更新,以避免AUKF降低跟蹤精度。

3 跟蹤濾波性能評估

基于低軌星網的多目標協同識別與跟蹤是一個多傳感器多目標問題,跟蹤目標的衛星個數隨時間變化,且由于多目標軌跡的不同,星網對每個目標的跟蹤效果也會有差異。為評估星網對多目標跟蹤識別性能,本文從對多目標的關聯準確度以及對多目標的跟蹤精度兩個方面建立評價指標。

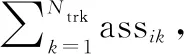
(42)

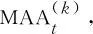
(43)

其中,N(k)表示對目標k的采樣總個數。

由于本文研究的是星網對多目標的識別與跟蹤問題,為了研究不同算法的性能對比,只考慮單個目標的跟蹤精度過于片面,由此需要引入一個指標綜合考慮對多個目標的估計結果。

為了評估多目標跟蹤問題的性能,將最優子模式分配(optical sub-pattern assignment, OSPA)距離應用于星網對多目標狀態估計的誤差分析。OSPA距離可以理解為p階逐對象式誤差。這個誤差由本地誤差和勢誤差組成。定義多目標t時刻的狀態估計值和真實值集合為

(44)

(45)

式中:Mt和Nt分別表示估計值集合和真實值集合,兩個集合的勢分別為mt和nt。對于任意正整數n∈N={1,2,…,n},Πn表示{1,2,…,n}排列的集合。OSPA距離定義為

(46)

(47)

式中:p為與階數相關的參數,決定了OSPA距離對錯誤估值的靈敏度;d(c)(Mi,Nπ(i))表示兩個向量之間的截斷歐式距離:

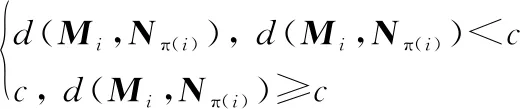
(48)

式中:d(Mi,Nπ(i))表示歐式距離,即

(49)

其中,c表示截斷參數。采用截斷歐式距離是為了避免某個估計值發散或估計值與真實值不匹配而導致的評估指標失效。

(50)

式中:c決定了分配給本地誤差和勢誤差的相對權重。

4 仿真分析

為了驗證所提出的多目標數據關聯與狀態估計算法的有效性和適用性,本節進行了數值仿真。仿真時長和采樣間隔分別設置為1 700 s和1 s,仿真開始時間設置為2020年11月25日04:00:00.00。考慮星基光學系統建立在構型如表1所示的Walker Delta型星座上;同時考慮如表2所示的多個目標。為了驗證所提算法的有效性,分別在多目標機動和非機動場景下利用星網對多目標進行跟蹤。

表1 星座構型

表2 多目標信息

4.1 非機動場景下仿真驗證

目標相距越近,目標的識別難度越高。為了驗證算法的有效性,設計目標1和目標3的運動軌跡相距很近,目標2和目標5的落點相近。在目標非機動的情況下,多目標的真實運動軌跡如圖3所示。

圖4為非機動場景下星網中可探測到目標的衛星個數。從圖中可以看出,由于目標和衛星均處于運動狀態,跟蹤目標的衛星數量實時變化,若在星間接力的過程中無法準確識別目標,則無法實現目標的連續跟蹤,或者導致濾波發散。圖5和圖6分別是采用本文算法得到的多目標位置和速度跟蹤誤差。從圖中可知本文所提出的濾波器能夠有效地利用星網實現多目標的識別跟蹤,對目標速度的估計誤差值大約500 s后就可以收斂到0.02 km/s以下,但是由于多傳感器間接力跟蹤的緣故,對位置的估計誤差沒有收斂到某一值附近,但是依然保持在10 km以下。

表3給出了非機動場景下星網對各個目標的MAA,從表中可以看出,對目標的MAA均在91%以上。但值得注意的是,分配精度會在某些時刻下降。這是因為在這些時刻,目標的實際位置非常相近,且由于跟蹤的無源性,其在像平面的角軌跡更容易相互覆蓋。雖然目標位置較近時對MAA有所影響,但是由于本文采用了卡方分布的原理,只采用較為可靠的量測值,在僅采用角軌跡的情況下依然能對多目標狀態進行準確估計。

表3 非機動場景下各目標的MAA

4.2 機動場景下仿真驗證

一旦目標進行機動,由于目標的非合作特性,因此無法提前獲知目標的機動序列,這會導致動力學模型的不準確,進而導致對目標狀態估計精度的降低。為此,本節測試了在目標機動場景下算法的性能。多目標的機動信息如表4所示。其中目標1、目標2、目標4為機動目標,機動開始/結束時間、機動幅度各不相同。值得注意的是由于這些目標的非合作特性,天基光學系統無法預先得知目標的機動信息。圖7展示了機動場景下5個目標的真實運動軌跡。

表4 多目標初始狀態和機動信息

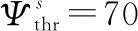
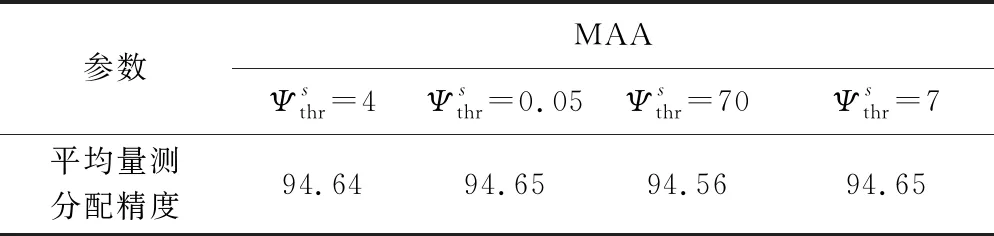
表5 機動場景下平均MAA

4.3 與其他算法的對比分析

利用低軌星網對多目標的識別跟蹤分為數據關聯階段和多目標狀態更新階段,且這兩個階段是迭代進行,為了驗證本文算法的有效性,本節采用不同的多目標狀態更新算法。將以VSUKF與AEKF、UKF和AUKF為狀態更新算法進行仿真對比,對比結果如圖10和表6所示。從表6中可以看出,VSUKF的MAA最高,說明在目標機動情況,與本節提到的其他算法相比,采用VSUKF作狀態更新濾波器的算法下可以對多目標進行更準確的數據關聯。從圖10可以看出,AEKF算法對位置和速度估計的OSPA距離明顯大于VSUKF和AUKF算法,這說明UKF算法的線性化誤差小于EKF算法,即UT變換比一階泰勒展開能更好地對非線性系統進行近似。從圖10(b)的結果可以看出,UKF算法在對目標速度估計方面比其他算法有更好的性能,而從圖10 (a)對目標位置的結果可以看出UKF在初始階段的OSPA距離相對較小,但在t=419 s時對目標位置估計的OSPA距離開始明顯增大,而這恰好是機動開始的時刻。這表明UKF在無機動情況下性能良好,但在目標機動時對位置的估計誤差顯著增大。t在0～750 s時AUKF的位置估計和速度估計的OSPA距離與VSUKF相似,而t在750～1 000 s時VSUKF的性能優于AUKF。這是因為t在750～1 000 s時目標未發生機動,均方誤差矩陣已經經過足夠的時間收斂到一個穩定的值。因此,本文提出的VSUKF已經切換到標準UKF,使得VSUKF和UKF對速度估計的OSPA距離幾乎相同,如圖10(b)所示。由此說明本文采用的VSUKF算法在機動和非機動階段都能得到滿意的估計,且與AUKF相比,它的計算量更小。

表6 不同算法的MAA

從以上仿真對比中可以看出,當目標處于非機動階段時,采用UKF算法的狀態估計精度要明顯高于AUKF算法;但是當目標處于機動狀態,由于UKF算法沒有考慮目標的機動特性,導致目標動力學模型不能準確反映實際情況,估計誤差增大,而AUKF算法則實現了較高的估計精度。本文提出的變結構濾波框架綜合考慮了估計精度和算法的計算量,通過機動檢測器進行UKF和AUKF之間的切換,既減少了計算量,又提高了估計精度。在本文提出的算法中,多目標數據關聯與目標狀態更新過程是迭代進行,緊密相連的,所以在VSUKF算法進行狀態更新基礎上進行的數據關聯結果也是較為準確的。

5 結 論

為了解決低軌星網對多目標的跟蹤問題,本文提出了基于卡方分布的多目標數據關聯算法和基于UKF濾波的多目標狀態更新算法。根據多目標在量測平面的量測殘差,基于卡方分布的假設,計算量測分配矩陣,在此基礎上,通過變結構濾波框架和UKF濾波對多目標的位置、速度和加速度信息進行估計。仿真結果表明,該算法在目標機動和非機動情況下均有效,且在較低的計算量下能夠達到與UKF和AUKF幾乎相同的估計性能。