基于LSTM的彈道導彈主動段軌跡預報

吉瑞萍, 張程祎, 梁 彥,*, 王躍東

(1. 西北工業大學自動化學院, 陜西 西安 710072;2. 信息融合技術教育部重點實驗室, 陜西 西安 710072)

0 引 言

彈道導彈因其速度快、射程遠、抗電磁干擾、高突防,甚至能運載核彈頭等特點,已成為國防安全面臨的最大威脅之一。為建立有效的導彈防御系統,相關學者進行了大量研究。在導彈防御系統的眾多技術環節中,彈道導彈長周期軌跡預報是至關重要的一環,因為其可以為防御系統提供響應時間,并為攔截器提供制導信息。

彈道導彈的整個軌跡通常分為3個基本階段:主動段、自由段和再入段。由于彈道導彈在后兩個階段受力相對簡單 (自由段僅受重力影響,再入段受氣動阻力和重力影響),傳統的軌跡預報方法大多集中在這兩個階段,根據解析法、數值積分法或函數逼近法推斷導彈的未來狀態。解析法將自由段軌跡近似為以地球為中心的橢圓,然后通過描述橢圓信息的開普勒模型進行軌跡預報。數值積分法根據一定的積分準則外推彈道導彈的動力學方程,進而得到目標軌跡的預報值。函數逼近法則是使用多個基函數的線性組合來對彈道進行逼近,從而預報未來彈道。自由段與再入段的軌跡可預測性使得大多數攔截方法主要面向這兩個階段。然而,彈道導彈在自由段會釋放多枚彈頭和誘餌,后兩階段的攔截將面臨目標識別的困難。相比之下,主動段攔截的優勢在于:目標導彈具有大而明亮的尾焰,使得導引頭容易追蹤目標位置,且無欺騙式干擾,攔截發生于敵國境內。基于上述考慮,有學者開展了彈道導彈主動段攔截方面的研究工作。為了給主動段攔截提供精確可靠的目標預報信息,本文對彈道導彈主動段長周期軌跡預報這一問題進行研究。

彈道導彈在主動段受到推力、氣動阻力和重力等未知力的影響,因此該階段的軌跡預報相比自由段和再入段更具挑戰性。受力的復雜性使得主動段軌跡不能用橢圓來近似。若考慮使用數值積分法從某一時刻的狀態估計開始外推彈道導彈動力學模型,由于經驗模型、量測等建模誤差的存在,目標狀態積分初值與彈道參數估計誤差的累積傳播會使長周期軌跡預報變得不可靠。函數逼近法原則上能夠用于彈道導彈主動段軌跡預報,但是需要根據主動段軌跡數據特征選擇合適的逼近函數空間,從而在預報精度與計算復雜度上獲得折中。因此,有必要研究有效的彈道導彈主動段軌跡預報方法。

近年來,已經開發了許多機器學習方法從大量數據中提取感興趣的知識,并且在航空航天領域獲得了廣泛的應用。例如,文獻[20]針對衛星通信非合作接收成對載波多址復用混合信號盲分離中高復雜度束縛,提出了一種基于前饋神經網絡的分離算法;文獻[21]將神經網絡和卡爾曼濾波器相結合,解決了航天器狀態估計和過程動態不確定性的估計問題。不同于一般的神經網絡,循環神經網絡及其重要變體——長短時記憶(long short-term memeory, LSTM)網絡,由于能夠有效提取序列上下文信息,在處理復雜時間序列問題上具有明顯優勢。例如,文獻[22]設計了一種基于深度LSTM的機動目標跟蹤方法估計與飛機運動序列一致的真實狀態;文獻[23]針對現有衛星通信系統無法適應信道時變問題,利用LSTM神經網絡建立了信噪比預測模型調整系統的調制與編碼方案;文獻[24]建立了基于LSTM的戰場意圖識別模型,以實現對戰場敵方目標戰術意圖的自動識別。

考慮到LSTM在處理時間序列上的優勢,本文提出了一種基于LSTM的彈道導彈主動段長周期軌跡預報方法。首先,根據彈道導彈主動段動力學模型及彈道參數典型取值生成軌跡庫,為待設計的網絡構建多樣化訓練樣本。其次,設計了基于深度LSTM的彈道導彈長周期軌跡預報算法。最后,與基于數值積分法、多項式擬合及反向傳播神經網絡的3種軌跡預報方法的實驗對比表明了所提方法在彈道導彈主動段軌跡預報上的優越性。

1 問題描述

本文的目的是根據對彈道導彈連續跟蹤至時刻的狀態估計值實現其主動段未來任意>時刻的軌跡預報。為此,需要首先確定彈道導彈主動段動力學模型與量測模型。

1.1 主動段動力學模型

如前所述,彈道導彈在主動段受到推力、氣動阻力與重力的作用。當采用常用的地心地固 (earth-centered earth-fixed, ECEF)坐標系描述其運動時,彈道導彈還受到科氏力與向心力的影響。因此,根據牛頓力學定律,彈道導彈主動段動力學模型為

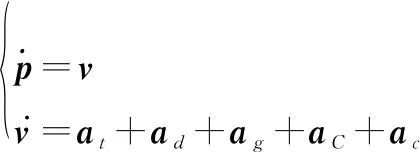
(1)

式中:=[,,]與=[,,]為目標在ECEF坐標系的位置與速度;,,,,分別為推力、氣動阻力、重力、科氏力與向心力加速度。

與文獻[7]類似,進行下述假設獲得加速度的解析表達式:

(1) 推力與速度方向一致;

(2) 火箭排氣速度和歸一化質量燃燒率為常數;

(3) 彈道系數為常數。

基于以上假設,有

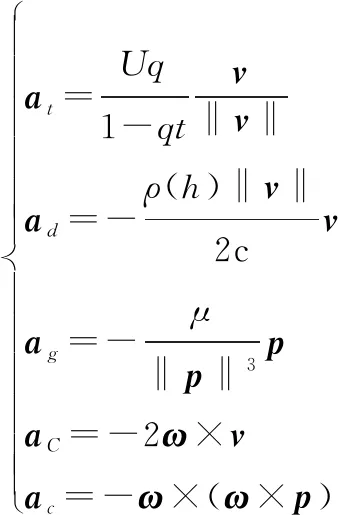
(2)

式中:代表時間;()=e- 為空氣密度;和為已知常數;=‖‖-為目標高度,為地球半徑;為地球重力常數;為地球自轉角速度;=[0,0,]。

將式(2)代入式(1),得到彈道導彈主動段位置與速度的衍化公式為

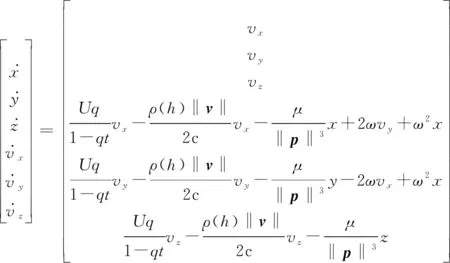
(3)

1.2 量測模型

=(-)

(4)

式中:=[,,]和分別為目標與雷達在ECEF坐標系中的位置;為ECEF至ENU坐標系的旋轉矩陣,表示為

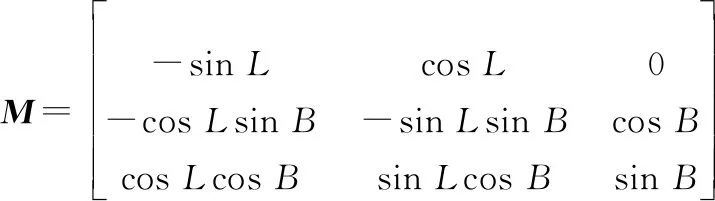
(5)

式中:和分別為雷達的經度與緯度。

因此,ENU坐標系中的量測模型為

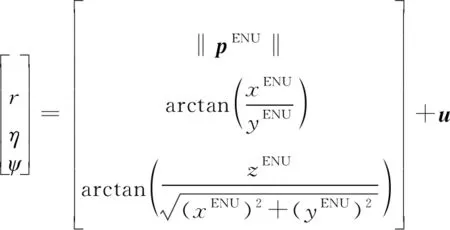
(6)

式中:為協方差矩陣等于的零均值高斯白噪聲。

1.3 主動段軌跡預報問題

彈道導彈主動段動力學模型,即式(3),能夠為彈道數據庫的生成提供依據;此外,還可以為用于目標狀態估計的跟蹤器的設計提供指導。但是,由于該模型中存在火箭排氣速度、歸一化質量燃燒率、彈道系數等未知參數,無法將其直接用于非合作導彈的軌跡預報。雖然可以通過期望最大化等方法獲得目標狀態和未知參數的聯合估計,但是無論選擇何種跟蹤器,這些估計值總是或多或少地帶有估計誤差。這里,采用靈敏度指標(定義為歸一化狀態變化率與歸一化控制變化率的比值)來定量分析軌跡控制變量 (即彈道參數和初始彈道導彈狀態)的估計不確定性對外推彈道的影響。

圖1描繪了相對于1%的軌跡控制變化量,方向上位置和速度分量的增量靈敏度。圖1(a)表明,彈道導彈軌跡相對于排氣速度和歸一化質量燃燒率的靈敏度高于彈道系數的靈敏度,這與文獻[7]的結果一致。另外,如圖1(b)所示,彈道軌跡對初始彈道狀態也具有很高的靈敏度 (對和方向上狀態分量的靈敏度分析可以獲得類似結果)。因此,基于跟蹤器輸出的導彈狀態與彈道參數估計值對動力學方程外推的軌跡預報方案是不可行的。

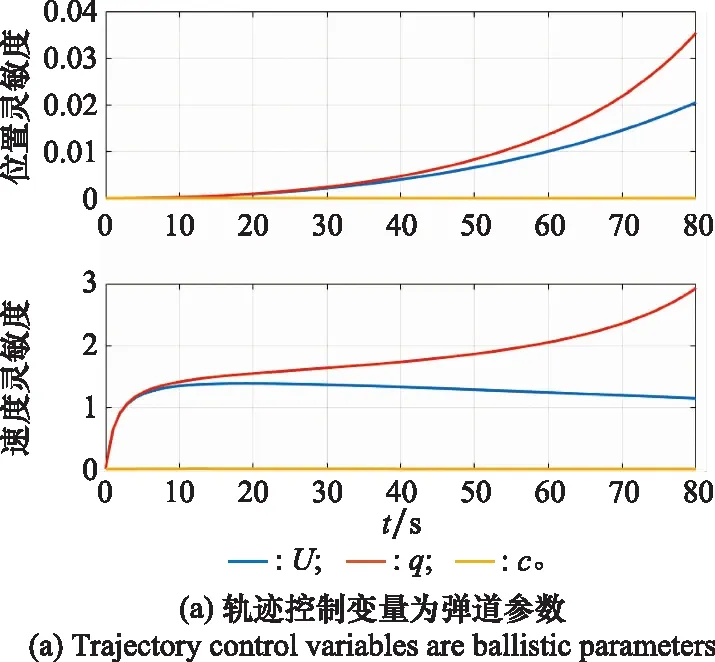
圖1 x方向上狀態分量對1%軌跡控制變化量的靈敏度

事實上,式(3)中的非線性及未知參數隱含在生成的彈道數據中。如果能夠獲得大量軌跡數據,就有可能學習出彈道導彈狀態隨時間的變化關系。因此,與其嘗試獲取盡可能準確的彈道導彈狀態和未知參數估計值對彈道進行外推預報,本文考慮利用LSTM網絡學習彈道導彈主動段軌跡庫中相鄰時刻目標狀態的變化關系,即構建的網絡實現如下功能:

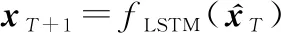
(7)

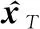
2 彈道導彈主動段軌跡庫生成

彈道導彈主動段軌跡數據來源有兩種:通過監視、偵察、情報收集等手段獲取部分關鍵彈道數據;利用主動段動力學模型及彈道參數典型取值生成目標導彈的彈道數據。由于神經網絡訓練需要大量樣本,本文采用第二種方法為基于LSTM的網絡提供豐富的樣本數據。

由于彈道參數與導彈類型相關,因此需對目標導彈的彈道參數在可行范圍內遍歷取值,以生成多條可行軌跡。另外,彈道導彈如果存在多級發動機助推,彈道參數還會面臨分級突變的問題。考慮到多級彈道導彈助推器的分離高度速度等關鍵信息難以獲取,本文構建單級中程彈道導彈主動段軌跡庫以驗證所提方法的有效性。

通過對文獻[27]中彈道參數的標稱值進行拉偏以實現彈道參數遍歷,并求解彈道導彈主動段動力學模型,生成了滿足中程導彈飛行時間與高度要求的10 000條主動段軌跡,如圖2所示。圖2表明建立的彈道軌跡庫可以覆蓋從指定位置發射的彈道導彈的大范圍攻擊區域。此外,表1總結了生成彈道導彈主動段軌跡庫的參數設置。

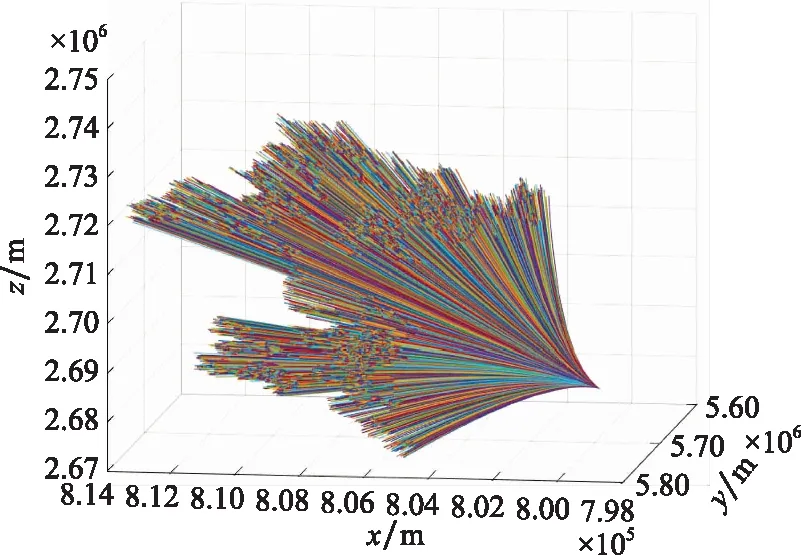
圖2 彈道導彈主動段軌跡庫

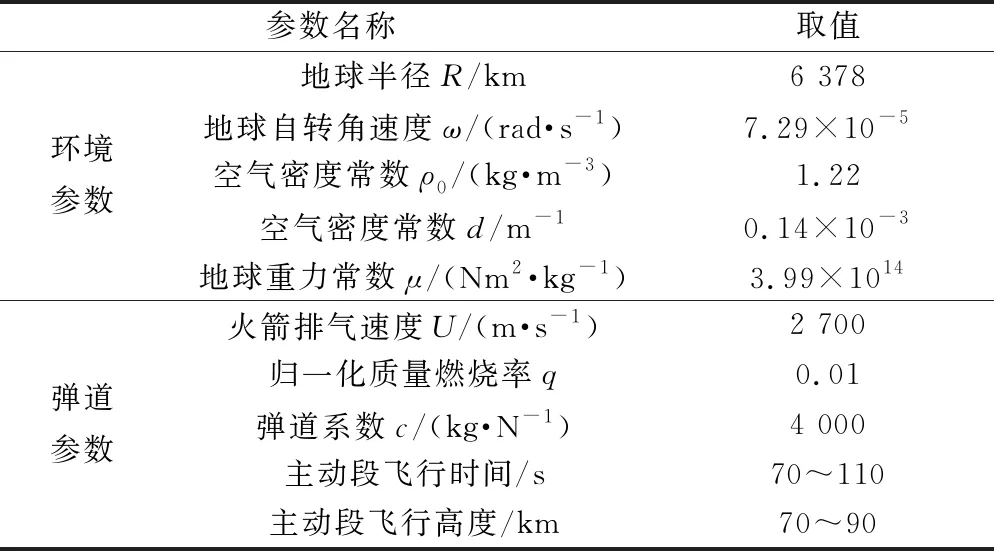
表1 彈道導彈主動段軌跡標稱參數

3 基于LSTM的軌跡遞歸預報方法

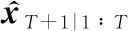
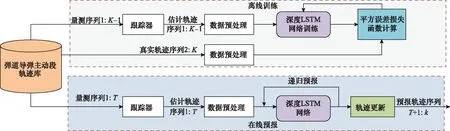
圖3 基于LSTM的彈道導彈主動段軌跡預報方案

3.1 數據預處理

3.1.1 軌跡分段

實際情況中,當對彈道導彈僅進行較短時長的持續觀測時,就可能有對其進行長周期軌跡預報的需求。因此,為使LSTM網絡在在線預報與離線訓練時的數據長度相匹配,需要將訓練集中每一條完整的主動段軌跡分割成長度為的若干軌跡片斷 (假設軌跡預報的最短持續觀測時長為個采樣周期)。這里以一條長度為的軌跡進行分段示例說明,如圖4所示。

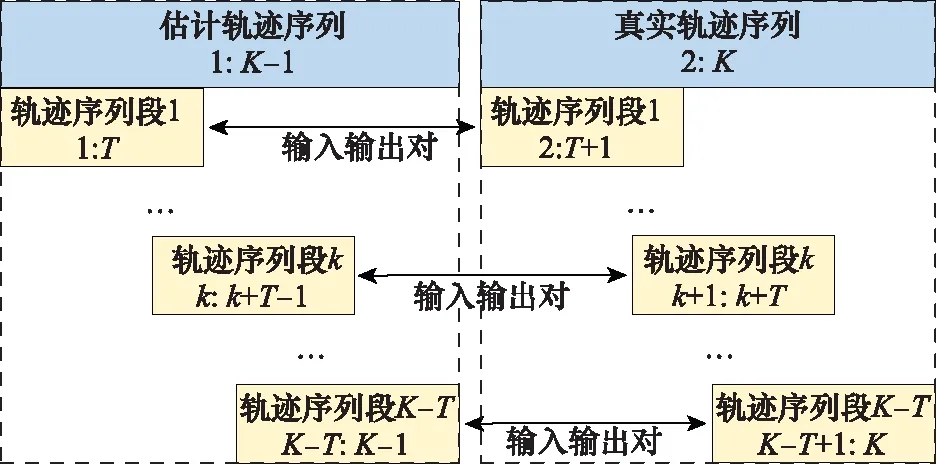
圖4 軌跡分段示例

3.1.2 數據歸一化

彈道導彈在主動段時,狀態不同維度之間量級相差很大,如圖2表明目標位置至少為10量級,而目標速度是從零開始累積的。如果將導彈狀態估計值直接輸入LSTM網絡并與網絡中的隨機權重矩陣進行前向計算,目標狀態中的速度特征將會被位置特征“淹沒”。此外,量級過大的位置輸入也會使第一層LSTM網絡中單元的激活函數工作在飽和區域,這將阻礙損失函數的反向傳播。為此,需要對用于彈道導彈軌跡預報的LSTM網絡的輸入輸出數據進行歸一化,以確保網絡的損失函數可以收斂到令人滿意的值。

本文對長度為的輸入輸出導彈軌跡序列采用最大值歸一化,即

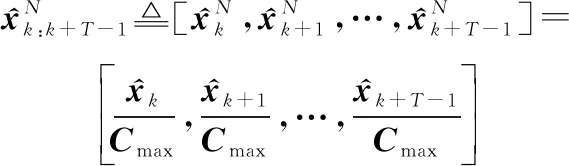
(8)

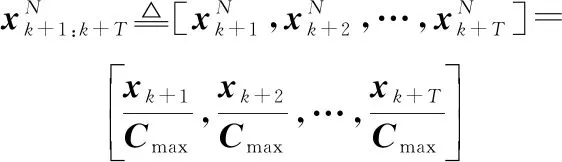
(9)

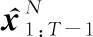
3.2 深度LSTM網絡訓練模型

本文設計的深度LSTM網絡包括3個LSTM層、一個最大輸出(Maxout)層和一個全連接(fully connected, FC)層,如圖5所示。3層LSTM網絡用于充分挖掘彈道導彈狀態之間的時序關系。Maxout層在第3層LSTM網絡的輸出空間中生成一個最大子集,其將網絡中對輸入數據不敏感的部分丟棄,僅訓練對輸入數據敏感的剩余網絡,以保證網絡更容易學習到輸入軌跡序列中的信息。FC層將Maxout層的輸出轉換為與軌跡預報序列具有相同維度的數據。

圖5 基于LSTM的彈道導彈主動段軌跡預報訓練模型

在誤差反向傳播階段,采用Adam算法對網絡進行優化直至收斂,其中損失函數定義為訓練軌跡樣本的正則化平方誤差:

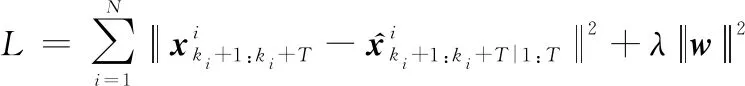
(10)

式中:為單步訓練的小批量樣本數;為自定義的懲罰項系數;為網絡中待學習的參數。

3.3 在線預報與軌跡更新

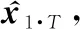
由于任意相鄰軌跡序列均存在長度為-2的重合預報時刻,對于預報長度為-的彈道導彈軌跡序列,+1≤≤-1之間的時刻由于神經網絡的遞歸外推會生成(2≤≤)個不同的預報值,因此需要將其平均以獲得時刻軌跡預報的更新估計。將各時刻更新后的軌跡預報值按時間順序排列,即可獲得完整的彈道導彈軌跡預報序列。

基于LSTM的彈道導彈主動段在線軌跡預報與更新方案如圖6所示。

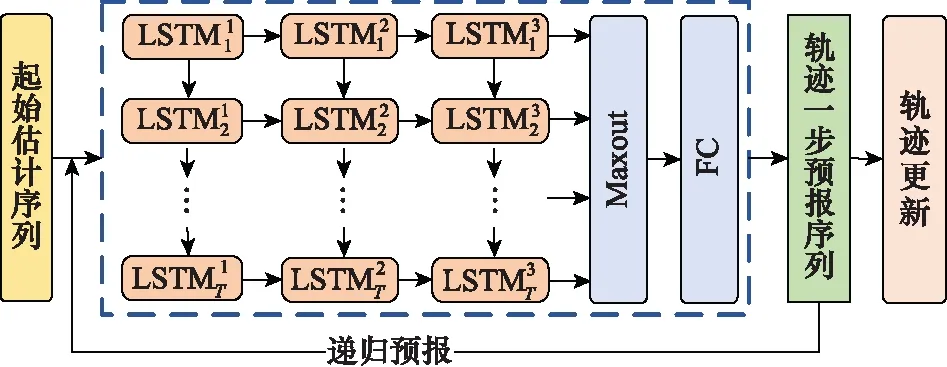
圖6 基于LSTM的彈道導彈主動段軌跡在線預報方案

4 實驗驗證

本節驗證基于LSTM的彈道導彈主動段軌跡預報(LSTM-based trajectory prediction, LSTM-TP)方法性能,包括參數設置、網絡收斂性分析與實驗結果3部分內容。

4.1 參數設置

實驗中涉及到的參數包括用于網絡訓練的超參數與樣本參數,各參數取值如表2～表4所示。

表2 不同網絡層神經元節點數設置

表3 網絡訓練參數設置

表4 樣本參數設置

為了分析網絡參數對平均預報均方根誤差 (average prediction root mean square error, APRMSE)和平均在線運行時間的影響,表3中列出了不同網絡參數取值下驗證集上的預報性能。可以看出,當網絡參數選為表3中第1列數值時,在驗證集上的整體預報性能是最優的。此外,表5還表明增加網絡結點數會增加LSTM-TP的平均運行時間,但不一定能提升APRMSE;增加訓練迭代步數也不一定能提升APRMSE。

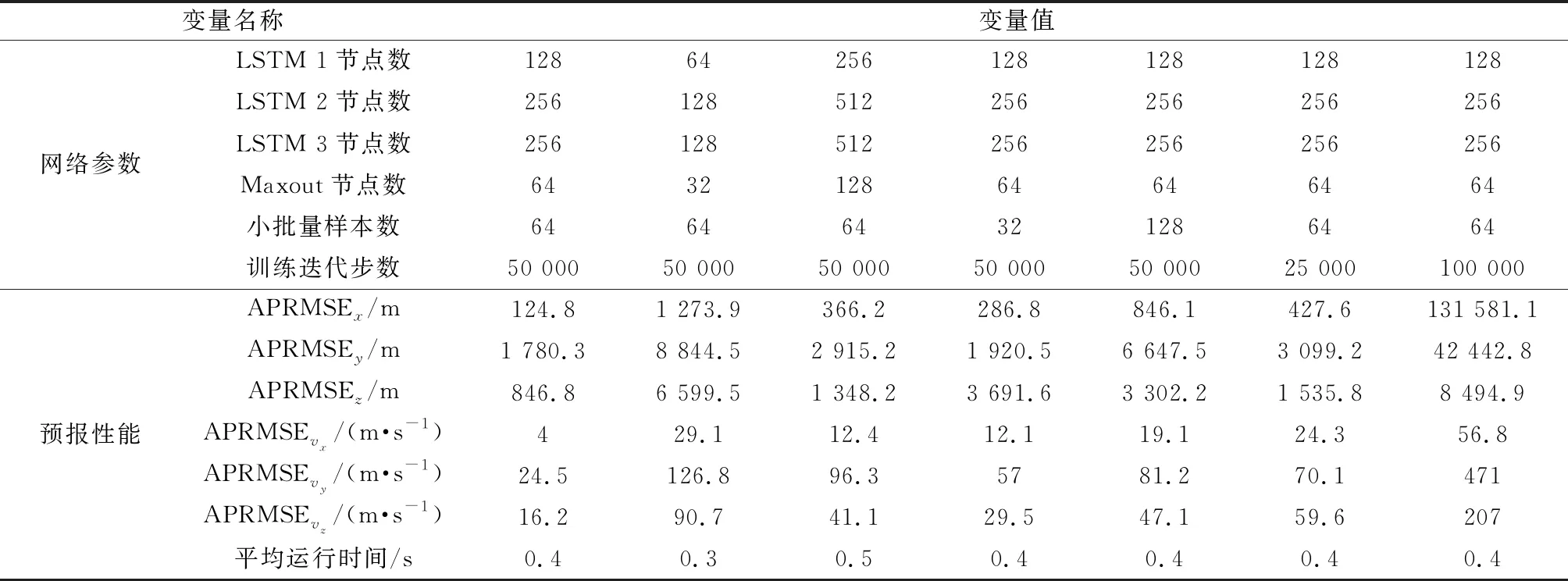
表5 不同網絡參數下驗證集預報性能分析

4.2 網絡收斂性分析

LSTM-TP網絡訓練過程中在驗證集上的損失如圖7所示,其中學習率以每5 000步指數衰減形式從10開始降低。可以看出,網絡在驗證集上的損失可以收斂到較好結果。

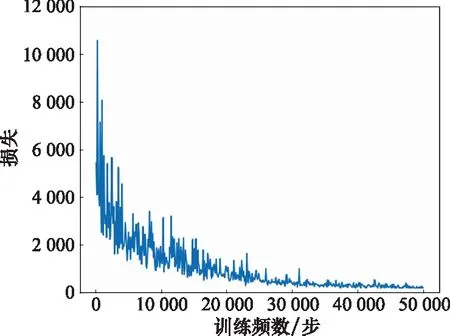
圖7 LSTM-TP網絡訓練過程中在驗證集上的損失

4.3 實驗結果

共進行了兩組實驗驗證。第1組將LSTM-TP方法與基于數值積分法、多項式擬合及反向傳播(back propagation, BP)神經網絡的彈道導彈軌跡預報方法進行了對比。第2組驗證軌跡估計序列長度對LSTM-TP方法的影響。所有軌跡預報方法用到的目標狀態估計序列均由URTSS-EM(uscented Rauch-Tung-Striebel smoother with expectation-maximization)算法提供,因為其可以較好地解決具有未知參數的非線性狀態估計問題。此外,量測模型中取值參考文獻[32],即徑向距、方位角、俯仰角的觀測誤差標準差分別為15 m, 0.1°, 0.15°。

4.3.1 實驗驗證1

本組實驗中,跟蹤器提供的彈道導彈狀態估計序列長度=10(采樣周期為1 s),需預報11～80 s之間的目標狀態。不同軌跡預報方法對彈道導彈位置與速度的預報均方根誤差如圖8所示。

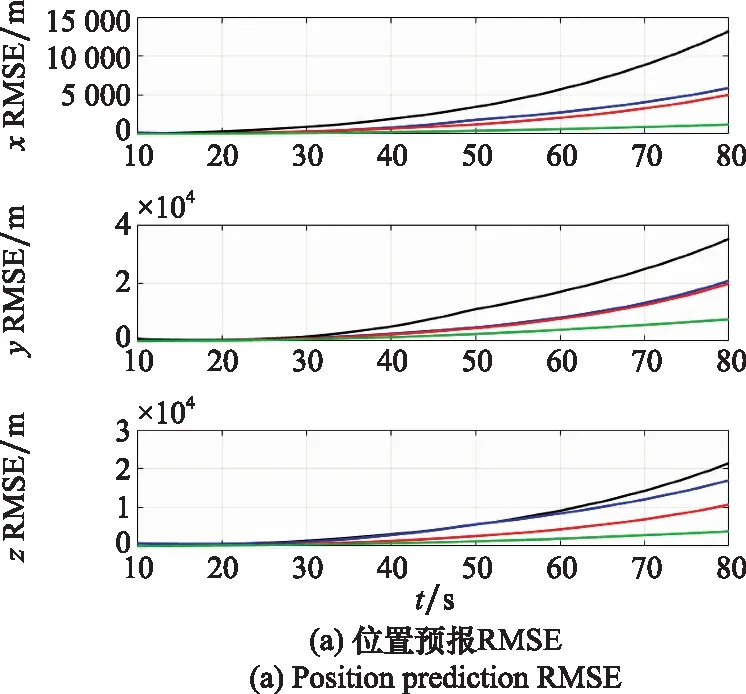
圖8 不同軌跡預報方法性能對比

可以看出,4種方法在彈道導彈主動段的長周期軌跡預報中均存在不同程度的發散。其中數值積分法的發散程度最高,這是因為目標狀態初值與彈道參數的估計誤差會在動力學模型的積分外推中累積傳播。多項式擬合法對累積至當前采樣時刻的目標狀態估計值進行最小二乘回歸,并用該回歸模型對未來時刻目標狀態進行預報,預報精度優于數值積分法。BP神經網絡與LSTM-TP方法由于利用了離線軌跡數據,預報效果整體上優于前兩種方法。相比于BP神經網絡,LSTM-TP能夠提取軌跡序列的時序特征,因此在彈道導彈主動段長周期軌跡預報中性能最優。

此外,表6中統計了4種軌跡預報方法的平均在線運行時間。雖然LSTM-TP方法的計算復雜度是最高的,但0.5 s的運行時間仍然能夠滿足彈道導彈主動段長周期軌跡預報的實際運行需求。

表6 4種軌跡預報方法平均在線運行時間

4.3.2 實驗驗證2

本組實驗中,跟蹤器提供的彈道導彈狀態估計序列長度分別為=5和=10(采樣周期均為1 s)。與第1組實驗相同,仍需預報11～80 s之間的目標狀態。LSTM-TP方法在不同估計序列長度下的軌跡預報性能如圖9所示。

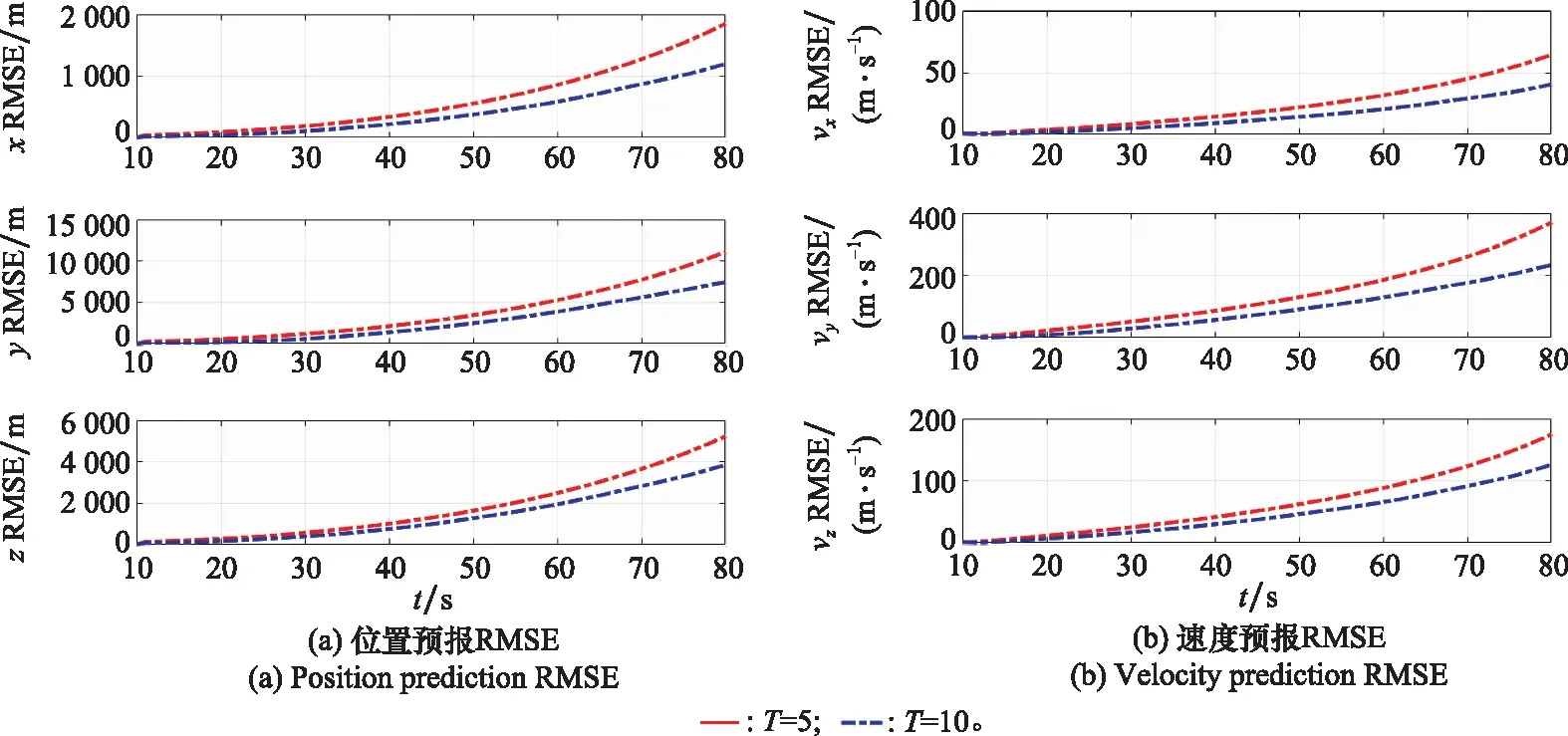
圖9 不同估計序列長度LSTM-TP軌跡預報性能對比

圖9表明,用序列長度=10的數據訓練的LSTM-TP網絡的性能要優于用=5的數據訓練的網絡。這是因為用于訓練的時間序列的長度越長,LSTM網絡記憶的時間信息就越多,對時間序列的擬合效果也就越好。因此,LSTM-TP方法在實際應用中,應積累盡可能長的彈道導彈軌跡估計序列,再進行長周期軌跡預報。

5 結 論

本文研究了彈道導彈主動段長周期軌跡預報問題,提出的解決方案為基于LSTM的深度神經網絡。得益于深度神經網絡強大的非線性擬合能力與LSTM對時間序列的記憶功能,設計的LSTM-TP方法通過對目標當前狀態估計序列的連續外推實現了未來軌跡的遞歸預報。最后,在彈道導彈主動段軌跡庫上證明了所提軌跡預報方法的有效性。