物體連滾帶滑問題的多種解法探析
——以第38屆全國中學生物理競賽預賽第8題為例

曾小江 曾 偉

（四川外語學院重慶第二外國語學校，重慶 400065）

2021年第38屆全國中學生物理競賽預賽第8題是一道關于均質小球連滾帶滑問題.解決連滾帶滑問題不能將物體視為質點，應視為另一理想模型——剛體.［1］均質剛體連滾帶滑問題蘊含豐富的物理思想和方法，是考查學生熟練掌握物理規律，靈活應用物理知識一類典型問題.通過對本題的分析求解，希望能加深學生對連滾帶滑問題的理解，提高學生運用物理規律多角度分析解決實際問題的能力.

1 原題及分析

解析：由題意可將小球的運動分為如圖1所示的3個運動階段.

圖1 小球運動示意圖

第2階段——連滾帶滑過程.小球與桌面的接觸點A的速度vA是質心平動速度vC和繞過質心軸轉動速度Rωt的合速度，即vA=vC-Rωt.在小球純滾動之前始終有vC＞Rωt，接觸點A相對桌面向右運動，小球在接觸點一直受到大小為f=μmg，方向水平向左的滑動摩擦力，摩擦力使平動減速，對質心軸的力矩使小球具有恒定的角加速度α，角速度從0開始均勻增加.小球的運動為質心向右做勻減速直線運動和繞過質心軸順時針加速轉動的疊加，即是連滾帶滑運動.

第3階段——純滾動過程.當小球與桌面的接觸點A的速度滿足vA=vC-Rωt=0，即vC=Rωt時，小球開始純滾動.不計球與桌面的滾動摩擦，小球在水平桌面的運動將不受摩擦力作用，小球將保持以平動速度為vC且繞過質心轉軸角速度為ωt的純滾動運動狀態.

以下求解均以擊打結束時刻為計時起點，來分析求解小球的運動.

2 多種解法探析

解法1.運用質心運動定理和轉動定理求解.

對小球運用質心運動定理有

得aC=μg，方向與質心運動方向相反.

小球質心做勻變速直線運動，由速度公式有vC=v0-aCt，即

以繞過質心的軸為轉軸，由轉動定理有

由角速度與角加速度的關系ωt=ω0+αt，得

小球與桌面接觸點的瞬時速度

將（2）、（4）式代入（5）式得

開始純滾動時接觸點A的速度為0，即

點評：根據小球的受力和運動情況，將小球的連滾帶滑運動分解為質心向右的勻減速直線運動和繞過質心軸順時針加速轉動.從動力學的角度運用質心運動定理求出質心的平動加速度aC.運用轉動定理解出小球繞質心轉動的角加速度α.應用運動學公式求出t時刻質心平動的瞬時速度vC和繞質心軸轉動的角速度ωt，而小球與桌面接觸點的瞬時速度為vA=vC-Rωt，可得出接觸點瞬時速度的表達式.再利用純滾動的條件vA=0，即可求得從擊打結束到小球開始純滾動的時間和此時的質心速度.此解法能清晰描述連滾帶滑運動全過程的物理特征.

解法2.運用動量定理和沖量矩表述的角動量定理求解.

設小球開始純滾動時質心速度為vt，從擊打結束到轉變成純滾動歷時為t，以水平向右為正方向.

對小球應用動量定理有

其中f=μmg，I=mv0.

選擇過質心且垂直運動紙面的軸線為轉軸，由沖量矩表述的角動量定理有

當小球開始純滾動時有

由（1）—（3）式可解得

點評：將小球的連滾帶滑運動分解為隨質心的平動和繞過質心軸的轉動.對小球隨質心的平動運用動量定理，繞過質心軸的轉動運用角動量定理，只需關注小球質心的初末速度和繞過質心軸轉動的始末角速度，無需考慮小球運動的演化過程，簡化了解題思維過程，是處理物體連滾帶滑運動的一種常用方法.

解法3.運用角動量守恒定律求解.

選擇過小球與桌面的接觸點O且垂直于紙面的軸線為轉軸，以垂直紙面向里為角動量的正方向，在運動過程中小球相對于過O點轉軸的力矩為0，小球對過O點轉軸的角動量守恒.小球對過O點轉軸的角動量為質心相對于O點的角動量與繞質心軸的角動量的矢量和.

點評：根據物體的受力情況，若能選取合適的轉軸（或參考點），物體相對于該轉軸的合力矩為0，則相對于該軸（或參考點）物體的角動量守恒，選取物體相對于該軸（或參考點）的初末狀態角動量，運用角動量守恒定律，可直接求出物體的運動狀態參量，簡化了解題過程.需要注意的是，物體相對于轉軸的角動量為物體質心相對于該軸的角動量與物體繞質心軸角動量的矢量和.

解法4.運用功能關系求解.

對小球質心的平動由質心運動定理有

設從擊打結束到開始純滾動小球質心沿相對于桌面的位移為s，對上式兩邊積分得

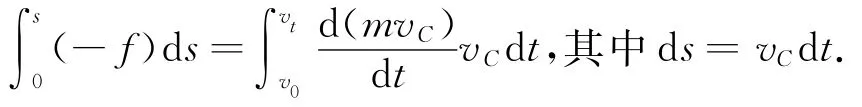
由積分可得

此式表明小球隨質心平動時，摩擦力所做的功等于小球平動動能的變化.

式中fRθ為小球繞過質心軸轉動時摩擦力所作的功.此式表明小球繞過質心軸轉動時摩擦力所作的功等于小球繞過質心軸轉動動能的變化.

結合（1）、（2）兩式，小球連滾帶滑過程的功能關系為

小球隨質心平動的位移

小球繞過質心軸的轉軸轉過的角度

從擊打結束到開始純滾動的時間t的解答過程同解法3.

點評：在本題的連滾帶滑問題中，小球質心平動速度vC大于繞過質心軸轉動速度Rωt（即vC＞Rωt），在質心平動方面，滑動摩擦力做功（-fs）使物體平動動能減少；在繞過質心軸轉動方面，滑動摩擦力做功（fRθ）使物體轉動動能增加，滑動摩擦力做功實現了物體平動動能向轉動動能的相互轉換，但總功為負值，使物體總動能減少.根據功能關系，滑動摩擦力做功等于物體動能的變化，列式可解出小球純滾動時的速度.

值得注意的是，上述各種解法都必須以分析清楚物體運動的初末狀態、受力情況和運動約束為前提.滑動摩擦力的方向與物體接觸點的速度方向相反，物體接觸點的速度是質心平動速度vC和繞過質心軸轉動速度Rωt的矢量和，即v=vCRωt.根據物體接觸點的速度方向確定物體在接觸點所受滑動摩擦力方向的方法：［2］（1）若vC＞Rωt，物體接觸點的速度方向與質心速度方向相同，滑動摩擦力方向與質心速度方向相反；（2）若vC＜Rωt，物體接觸點的速度方向與質心速度方向相反，滑動摩擦力方向與質心速度方向相同；（3）若vC=Rωt，物體接觸點的速度為0，物體純滾動，不受滑動摩擦力作用.

3 總結

綜上所述，對于物體隨質心平動和繞過質心軸轉動的連滾帶滑運動問題，可從4個角度進行分析求解：（1）從運動學和動力學的角度運用質心運動定理和轉動定理進行求解，可清晰的描述運動變化的全過程；（2）從動量定理和角動量定理的角度，對質心的平動運用動量定理和對繞過質心軸的轉動運用角動量定理進行求解，只需關注運動的初末狀態；（3）根據物體的受力情況，若能選擇合適的轉軸（或參考點），使各力對該軸（或參考點）的力矩為零，運用角動量守恒定律求解，可簡化解題過程，計算簡單，但此法只能在選取到合適的轉軸條件下使用；（4）在連滾帶滑運動中，滑動摩擦力所做的功是物體隨質心平動時摩擦力所作的功和物體繞質心軸轉動時摩擦力所作的功的代數和，從功能關系的角度，運用動能定理求解，只需明確物體初末狀態的動能.

以上4種解法涉及的知識幾乎涵蓋了力學的大部分主干內容，在解決問題的思路上實現了從常規思維向高階思維的轉化，充分展現了運用物理規律解決生活實際問題上方法選擇的靈活性、多樣性，對啟發學生運用物理規律多角度探索生活中的實際問題，提高學習興趣都很有意義.