基于BP 神經網絡的沙柳地上生物量預測模型

程冀文，王樹森＊，羅于洋，張 岑,2

(1. 內蒙古農業大學沙漠治理學院，荒漠生態系統保護與修復國家林業和草原局重點實驗室，內蒙古 呼和浩特 010018；2. 清水河縣老牛灣鎮人民政府 內蒙古 呼和浩特 011614)

沙柳（Salix psammophilaC.Wang et Ch.Y.Yang）又名北沙柳，在庫布齊沙漠有廣泛分布，常作固沙造林樹種[1-2]，也是我國北部地區防風固沙的優良樹種和當地典型的能源樹種[2-3]。通常情況下，沙柳在沙丘中下部有少量分布，在灘地沙區大量密集分布[4]。沙柳具備生長速率較快的特點，并且人工栽培沙柳在短時間內就能產生體積很大的灌叢，因此能夠在水土保持與荒漠化防治、水源涵養、氣候調節等生態效益方面起到重要的作用[5]。由于沙柳木質優良，還可以廣泛用于造紙、人造板等工業用途[6]。

在干旱半干旱風沙區，沙生灌木有著防風固沙、水土保持等作用，通常野外調查使用的直接收割法會對地表造成破壞從而發生土壤侵蝕現象[7]。因此探究灌木生物量與易測因子間的關系，建立沙生灌木生物量模型對沙生灌木生物量研究有很大的助力。目前，國內外學者在生物量模型方面有大量的研究[8-10]，通常選取林木因子作為自變量構建灌木生物量模型，但是由于各區域之間自然環境條件的巨大差別，以及不同氣候區灌木植被的形態特性等具有很大不同，因此很多地區灌木的生物量預測模型僅在當地有較好的解釋力。因此對于灌木構建適應其生境的生物量預測模型是十分必要的[11]。

近年來，許多學者將BP 神經網絡應用在林業上[12-14]。研究發現，BP 神經網絡模型精度相較于傳統更好[15-19]。但是目前的研究大多集中在高大喬木的生物量估算方面，對于運用BP 神經網絡進行灌木，尤其是沙生灌木的生物量估算卻鮮有報道。因此，利用沙柳的不同林木因子建立BP 神經網絡生物量估算模型，探究BP 神經網絡在沙生灌木生物量方面的應用是必要的。本研究以庫布其沙漠沙柳為研究對象，建立了沙柳BP 神經網絡的生物量預測模型，探究不同林木因子對沙柳BP 神經網絡生物量預測模型的影響，以期為沙柳以及其他沙生灌木生物量建模與估測工作提供參考依據。

1 材料與方法

1.1 研究區概況

研究區域地處庫布齊沙漠，處于鄂爾多斯市杭錦旗獨貴塔拉鎮境內，地理坐標為108°15′～108°24′ E ，40°48′～40°39′ N ，屬于典型溫帶大陸性干旱、半干旱季風氣候。年均降水量約400 mm[20]。其范圍內木本野生植物主要有小葉楊（Populus simoniiCarr）， 沙 棗（Elaeagnus angutifoliaLinn）， 沙 柳（Salix psammophilaC.Wang et Ch.Y. Yang）等[6]。

1.2 研究方法

1.2.1 數據采集 外業數據采集時間為2017 年4 月。在研究地選擇迎風坡風蝕、丘間低地沙埋和未沙埋3 種立地條件，共選擇91 株沙柳。根據沙柳的形態學特性，選取用于BP 神經網絡生物量預測模型建模的因子有叢高（H）、地徑（D）、冠幅（C）、基部分支數（Nt）、單枝最大分支數（Nb）、單枝最大分枝次數（Nbt）、枝條粗度（Db）、芽眼數（Ne）。采用皮尺和游標卡尺對以上林木因子進行測量和記錄（表1）。記錄工作結束后，將所選取的沙柳齊地面刈割，使用電子天平現場稱取鮮質量。將現場刈割的沙柳枝條帶回實驗室使用烘箱70℃烘干24 h 至恒質量，使用天平稱取干質量，計算沙柳地上部分生物量。

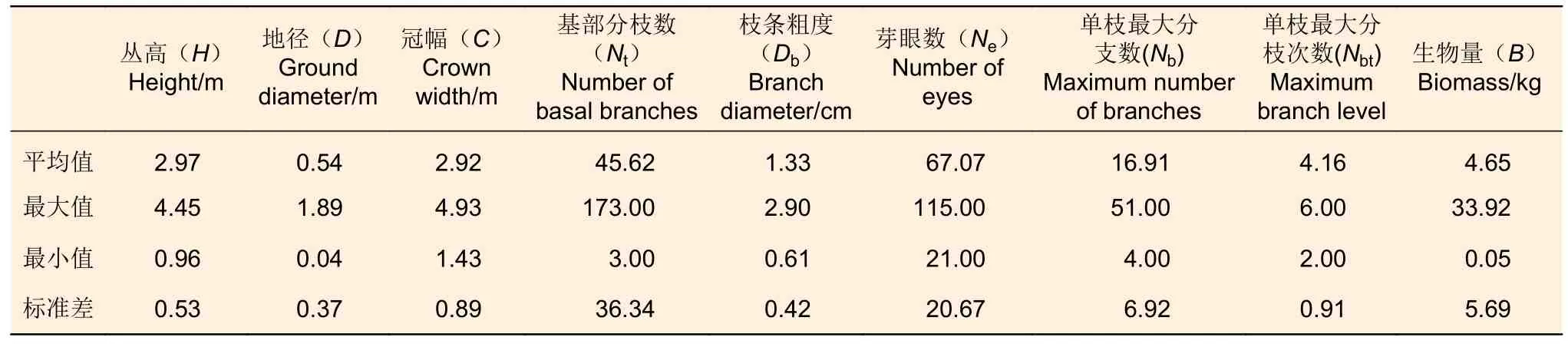
表1 建模數據統計Table 1 Summary statistics for model modeling and validation

1.2.2 BP 神經網絡 BP 神經網絡由包括輸入層、隱層和輸出層共3 部分組成（圖1），BP 神經網絡中神經元結構如圖2 所示，x1～xn(1, 2,3, ···,n)為輸入信號，ω1～ωn(1, 2, 3, ···,n)為權重，b為偏置，∑為求和節點，σ為激活函數。按照Kolmog-orov 定理，單隱層的BP 神經網絡將能夠無限接近任意連續的非線性曲線[21]。但過分擬合會導致模型的泛化能力差，所以在實際的應用中還要結合樣本本身的特性來控制擬合程度。

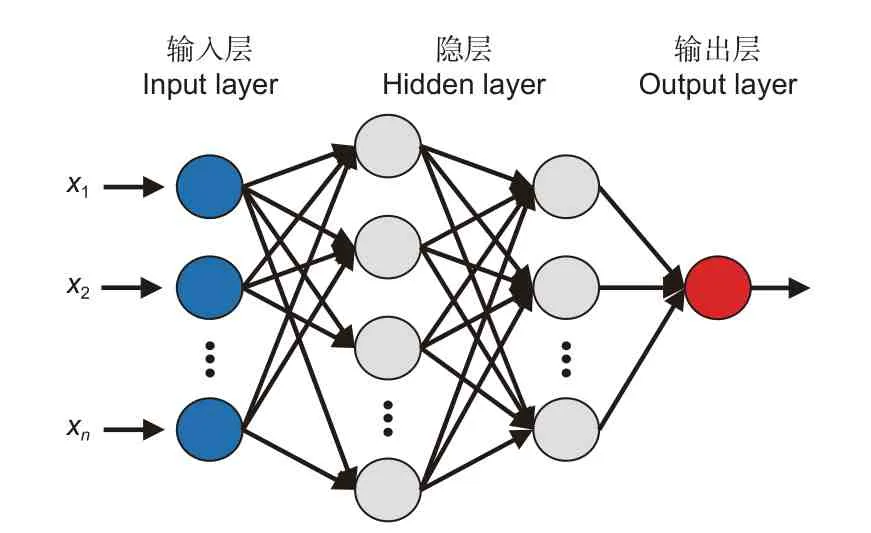
圖1 BP 神經網絡結構Fig. 1 Structure of BP neural network

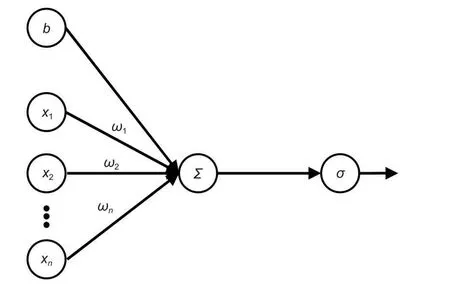
圖2 神經元結構Fig. 2 Neuron structure

1.2.3 BP 神經網絡模型的建立 構建沙柳BP 神經網絡生物量預測模型使用Matlab 軟件中的nntool 工具箱，以沙柳林木因子作為輸入層，沙柳生物量實測值為訓練目標。為確定BP 神經網絡的隱層節點數的經驗公式，其中：Nh為隱層節點數，Nin為輸入層節點數，Nout為輸出層節點數，對比其估測精確度及泛化能力以確定最佳隱層節點數。建模時，設置目標精度為0.001，最大迭代次數為1 000，學習率為0.01，隱層傳遞函數為logsig，輸出層傳遞函數為purelin，使用后的模型訓練算法為L-M 算法。

1.2.4 歸一化處理與反歸一 對于參與建模的數據采取歸一化處理，可以讓神經網絡的訓練效率有所提升，并且在擬合后還必須對輸出數據采取反歸一處理，使輸出數據重新轉換回沙柳的生物量的輸出值。據此，本研究通過下列公式對輸入因子數據和輸入目標數據進行歸一化處理：

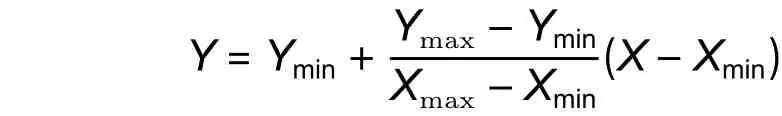
式中：X為未進行處理的值；Xmax、Xmin為代表未進行處理數據組中的最大和最小值；Y為進行處理后的值；Ymax和Ymin分別為進行處理后的數據組中的最大和最小值。

當BP 神經網絡擬合結束后，對所得數據進行反歸一處理，也就是將程序運行得到的數據映射到實際預測值。

1.2.5 模型評價與檢驗 采用決定系數R2，均方根誤差（RMSE）和平均絕對誤差（MAE）對模型性能進行評價。

2 結果與分析

2.1 模型輸入因子的篩選

前期可供作為輸入因子的備選指標有叢高（H）、地徑（D）、冠幅（C）、基部分支數（Nt）、單枝最大分支數（Nb）、單枝最大分枝次數（Nbt）、枝條粗度（Db）、芽眼數（Ne），對各因子與生物量（B）之間進行相關性分析，結果如圖3 所示。

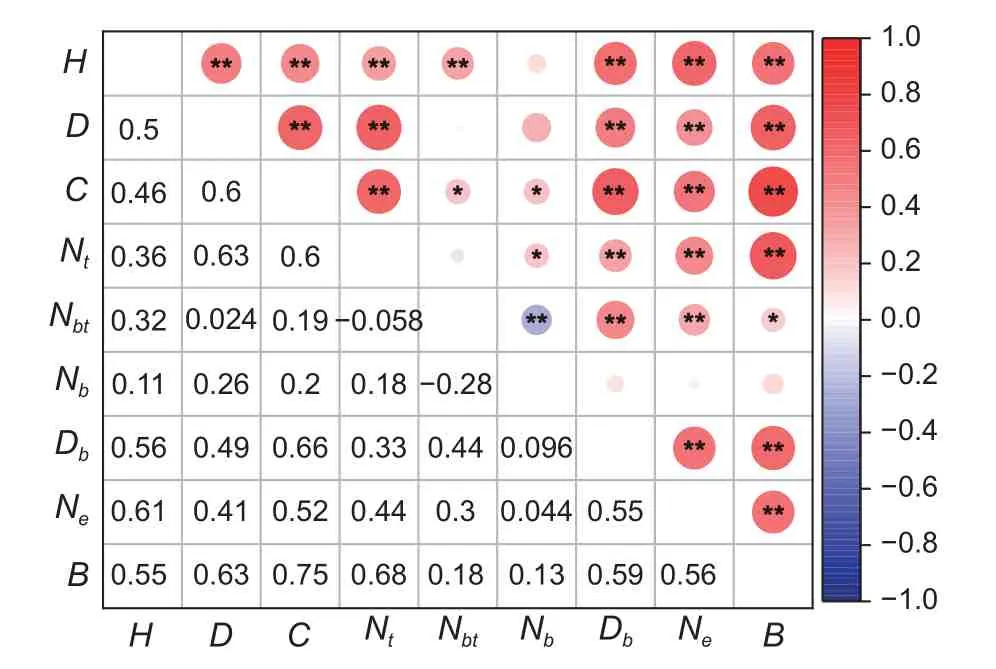
圖3 沙柳各因子相關性分析Fig. 3 Relationship of factors inSalix psammophila

其中各因子與生物量相關性表現為：冠幅（ 0.751） ＞基 部 分 支 數（ 0.677） ＞地 徑（ 0.631） ＞枝 條 粗 度（ 0.589） ＞芽 眼 數（0.555）＞叢高（0.550）＞單枝最大分枝次數（0.179）＞單枝最大分枝數（0.132），其中叢高、地徑、冠幅、基部分支數、芽眼數、枝條粗度與生物量間表現為極顯著相關（P＜0.01）；單枝最大分枝次數與生物量間表現為顯著相關（P＜0.05）；單枝最大分枝數與生物量之間顯著相關。由此選取叢高、地徑、冠幅、基部分支數、芽眼數、枝條粗度為模型最終輸入因子。對于傳統生物量模型而言，將叢高、地徑、冠幅、基部分支數、芽眼數、枝條粗度分別作為自變量擬合生物量模型。對于BP 神經網絡模型而言，根據其相關性高低逐個加入模型輸入層，確定輸入層為輸入因子數為1～6。

2.2 BP 神經網絡模型的建立

根據相關性大小，共設置6 組輸入變量Nin分別為1～6。輸出變量Nout為生物量。由于輸出值都為1，輸入變量為1～6，則根據經驗公式可得，當輸入因子數為1 時，BP 神經網絡隱層數Nh的取值范圍為2.41～11.41之間；當輸入因子數為2～5 時，BP 神經網絡隱層數Nh的取值范圍最小值為2.73～3.45，隱層數Nh的取值范圍最大值為11.73～12.45；當輸入因子數為6 時，BP 神經網絡隱層數Nh的取值范圍為3.65～12.65。由于神經網絡訓練結果有一定的波動，為增加模型的容錯率，則將隱層數Nh選取為整數，當輸入因子數為1 時，BP 神經網絡隱層數Nh的取值范圍為2～11 的整數；當輸入因子數為2～5 時，BP 神經網絡隱層數Nh的取值范圍為3～12 的整數；當輸入因子數為6 時，BP 神經網絡隱層數Nh的取值范圍為4～13 的整數。對不同輸入因子數各10 隱層的模型分別訓練10 次，不同輸入變量擬合情況見表2。

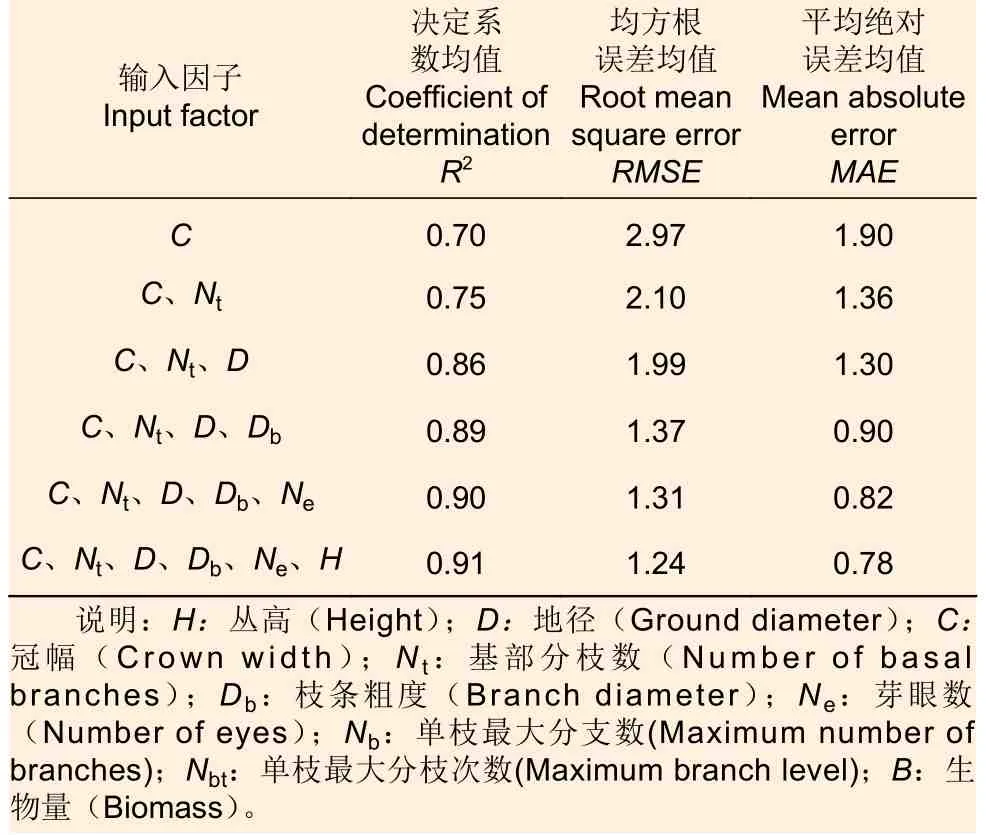
表2 BP 神經網絡模型不同輸入變量擬合優勢度評價Table 2 Evaluation of fitting dominance of different input variables in BP neural network model

可以看出，模型的精度隨著輸入因子個數的增加而增加（圖4），當輸入因子數量為5 時，模型精度相比輸入因子數量為4 時提升不明顯，為了平衡模型的易用性和精度，則選擇4 輸入因子為模型的最優輸入變量數。

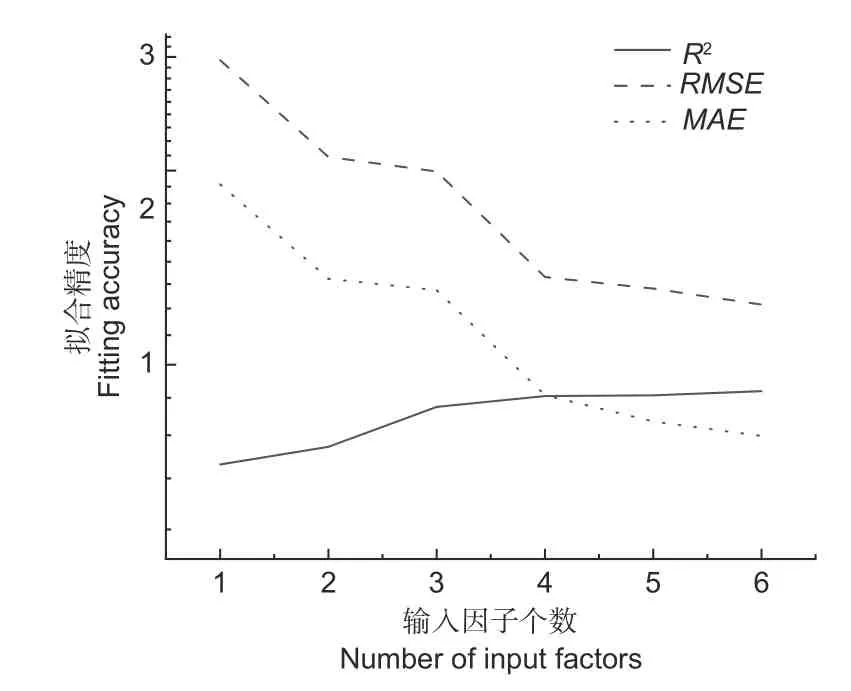
圖4 隨著輸入因子增加模型性能變化Fig. 4 Fitting accuracy with different number of input factors

2.3 BP 神經網絡最優模型的確定

當輸入因子數為4 時BP 神經網絡隱層數Nh的取值范圍為3～12 的整數，不同節點數的模型擬合情況(見表3)，其中當隱層數為9 時，其R2在各隱層數中表現為最大，RMSE和MAE表現為最小，由此得知，當隱層數為9 時，模型擬合效果最好。

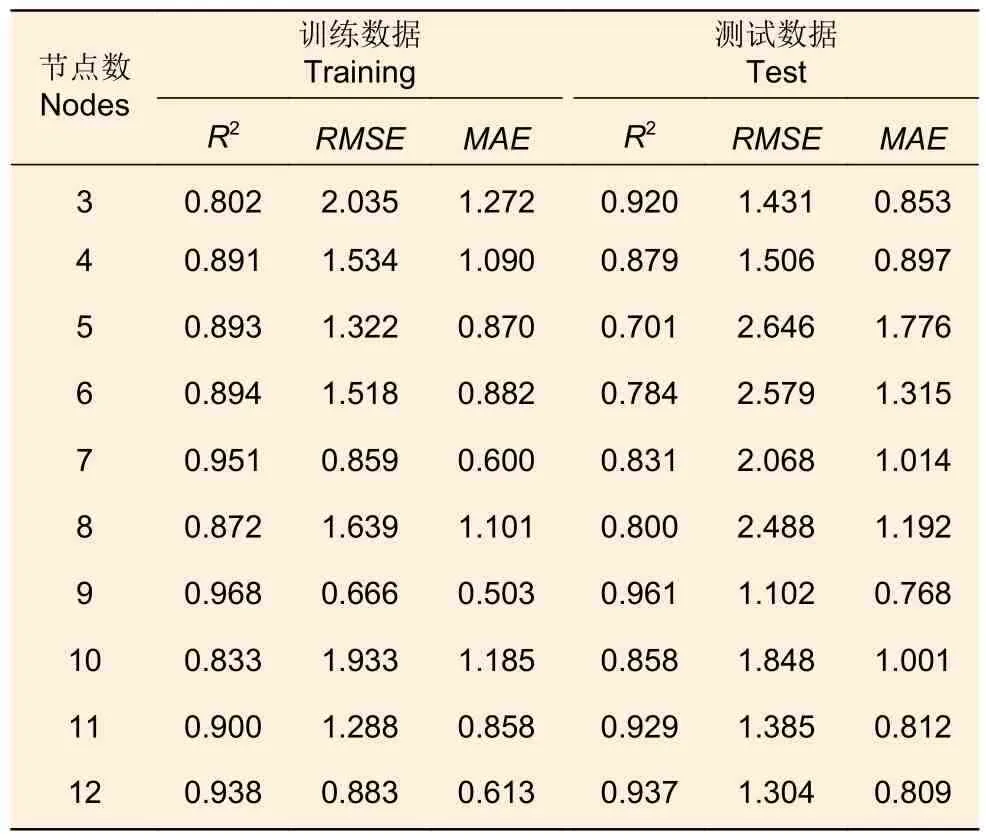
表3 輸入因子數為4 時BP 神經網絡模型擬合優勢度評價Table 3 Evaluation of fitting dominance of BP neural network model when the Ninfactors is 4

由此，最佳輸入變量和最佳隱層數確定后，在同一個隱層節點數的基礎上不斷訓練模型，最終選擇合適的結構為最后的模型，其中：最優結構[輸入層節點數(Nin)∶隱層節點數(Nh)∶輸出層節點數(Nout)]=4∶9∶1。經過訓練所得傳遞函數模型為：

H= purelin (1.506 1h1+ 1.151 6h2+ 0.226 53h3?1.447 2h4?0.234 79h5+ 1.225 4h6?1.263 5h7?0.155 27h8?2.062 6h9?0.853 28)；

h1= logsig (0.844 89C+ 1.865 2Nt+ 3.207 6D?4.063 2Db+ 6.167 7)；

h2= logsig (6.942C+ 0.381 08Nt+ 4.981 5D?1.046 5Db?5.647 2)；

h3= logsig (1.635C?2.413 6Nt?0.163 18D?4.040 7Db?2.106 9)；

h4= logsig (0.940 89C+ 2.839 6Nt?6.912 5D?1.823 8Db?1.757 9)；

h5= logsig (1.224C?2.715 7Nt?2.839 4D?4.562 5Db?2.169)；

h6= logsig (1.193 2C+ 3.811 7Nt?7.989 1D?0.911 14Db?0.853 18)；

h7= logsig (1.955 4C?2.838 1Nt+ 2.935 2D?1.89Db+ 3.127 6)；

h8= logsig (?3.880 3C+ 0.570 5Nt?2.167 3D?2.634 9Db?3.617 8)；

h9= logsig (?3.781 5C+ 2.025 1Nt+ 2.536 2D+0.408 18Db?4.022 4)；

3 討論

灌木生物量模型應選擇所研究灌木的易測因子作為模型構建的自變量，往往不同形態特征的灌木，宜采用不同的變量構建生物量模型，所以應根據所研究灌木的形態特征來選取最優灌木易測因子作為模型構建的自變量[11]。由于BP 神經網絡模型的自身特性，增加輸入變量的數量，可以使得模型的泛化能力提高，增加模型精度[22-23]。對于本研究來講，模型輸入變量盡可能的囊括沙柳所有可以測量的形態指標，并以沙柳各因子與沙柳生物量的相關關系為基礎進行篩選，在最優模型中輸入因子包括冠幅C、基部分支數Nt、地徑D、枝條粗度Db共4 種。輸入變量中輸入因子數量的增加可以使得模型精度不斷上升。

在風沙區，由于風大沙多，灌木基部容易產生沙埋的現象，使得基徑的測量比較困難，考慮到模型在日常生產中的易用性和實用性，在構建生物量模型時要結合實際工作考量不同的建模因子[24]。本研究中地徑與生物量相關性為0.631。如果使用相關性不如地徑但更為簡單易測的兩個或多個因子進行建模，是否在模型性能上可以替代相對不易測的地徑參與建模的模型呢？在未來的沙區灌木生物量模型研究中，應將實際工作中灌木因子的測量難易程度加入建模輸入因子篩選的條件中，對比低相關但相對易測因子與高相關性但測量困難的因子對生物量估算模型性能的影響。

本研究選擇6 種BP 神經網絡的輸入因子均為沙柳的測樹因子，并未包括環境因子，將林分因子和氣候因子等變量共同參與生物量預測模型的擬合，對于模型的性能有較大的提高[17]。坡向、坡位、立地條件、海拔和林分密度等環境因素對林木的生長發育也有很大的影響，將以上因子加入到模型的擬合會有效提高模型精度[25]。本研究中尚未將丘間低地未沙埋、丘間低地沙埋、迎風坡風蝕3 種立地條件考慮到模型的建模當中，接下來的研究中要探究不同立地條件對的沙柳BP 神經網絡生物量預測模型的影響。

4 結論

本研究以庫布其沙漠沙柳為研究對象，為其分別建立傳統沙柳生物量模型和基于BP 神經網絡的沙柳生物量模型，探究不同建模因子下的沙柳生物量估算模型變化。根據沙柳生長因子相關性大小，輸入變量所包含的輸入因子由1 種逐漸增加至最大6 種，擬合發現，隨著輸入變量中輸入因子的數量不斷增加，輸入變量達到6 種時R2（0.91）、RMSE（1.24）、MAE（0.78）所表現出的模型性能最好，輸入變量每增加1 種后，模型性能提升幅度不盡相同，當輸入因子數量為5 時，模型精度相比輸入因子數量為4 時提升幅度較小，考慮到在模型使用時要同時兼顧其使用精度和野外實地調查時的工作強度和調查量大小，故選擇輸入變量中，輸入因子為4 種時為最佳，則其輸入層最優輸入因子數為4 種。在確定模型結構輸入為4，輸出為1 的前提下，對模型各隱層數不斷訓練，當隱層數為9 時，模型性能表現為最優，則基于BP 神經網絡的沙柳生物量估算模型最優結構[輸入層節點數(Nin)∶隱層節點數(Nh)∶輸出層節點數(Nout)]=4∶9∶1。