一種采用遺傳算法優化Chaboche模型的轉子輪盤疲勞壽命預測方法

史昱昆 王恭義 程 凱 葉篤毅

（1.浙江大學化工機械研究所；2.上海汽輪機廠有限公司）

在發電設備中，單缸汽輪機相比多缸汽輪機具有成本低、熱效率高及結構緊湊等優點［1］。作為單杠汽輪機的關鍵部件，一體化轉子在服役時需要滿足快速啟停、變負荷等要求。 在上述交變載荷作用下，轉子輪盤應力集中部位（如輪槽齒根）通常存在明顯的平均應力，并伴隨啟停過程出現平均應力循環松弛行為［2，3］，因此，在一體化轉子的抗疲勞設計中，如何考慮平均應力的影響成為重要的研究內容。

對于平均應力松弛的定量描述，目前工程上主要有兩類常用方法：一類是經驗模型，另一類是循環塑性本構模型［4］。 由于循環本構模型只需開展少量試驗就能完整模擬材料的應力應變行為，近年來已被越來越多地用于描述疲勞載荷下平均應力循環松弛［5］。 其中，Chaboche模型是目前應用廣泛的循環本構模型之一［6］。 Chaboche模型最初采用了3級背應力形式。 近年來，為了進一步提高模型的預測精度， 在3級背應力基礎上又發展了多級背應力模型［7］。 例如：姜金朋等采用4級背應力模型預測了CS1026 材料的單軸棘輪效應［8］；Mahmoudi A H等提出5級背應力模型來改進Chaboche模型的預測能力［9］；Ohno N和Wang J D采用分段線性劃分方式，發展了級數更多（8級，12級）的背應力模型［10］，但隨著背應力級數增加，也帶來了模型參數大幅增加、參數確定困難等問題。 為了克服傳統參數確定方法（如試驗法結合試錯法［11］）存在的求解精度低的問題，近年來許多學者引入了遺傳算法來優化Chaboche本構模型中的參數。例如，Nath A等通過對穩定滯回環獲取的Chaboche參數進行基因算法優化， 提高了多種CSMs材料棘輪效應的模擬精度［12］。 Mal S等分別采用試錯法和基因算法模擬20MnMoNi55鋼的滯回環，結果表明：Chaboche模型對參數的敏感程度很高， 參數經過優化后使得結果更為精確［13］。Mahmoudi A H等采用多目標基因算法，將每個循環的最大應變考慮到誤差函數中，模擬了多種材料的棘輪效應［14］。 Rouse J P等采用單目標基因算法， 預測了P91鋼在600 ℃下的應力應變響應，取得了較好的效果［15］。 由此可以看出，采用遺傳算法優化Chaboche本構模型參數能夠顯著提高疲勞壽命預測的精度，具有廣闊的應用前景。

筆者針對某汽輪機一體化轉子輪盤的抗疲勞設計需要，采用局部應變法，并結合基于遺傳算法優化的8級背應力Chaboche模型，來研究考慮平均應力動態松弛行為的輪盤輪槽疲勞壽命預測方法。

1 基于Chaboche模型的轉子輪盤疲勞壽命預測方法

1.1 Chaboche模型及其參數確定算法

Chaboche模型基于Von Mises屈服準則，其表達式為：

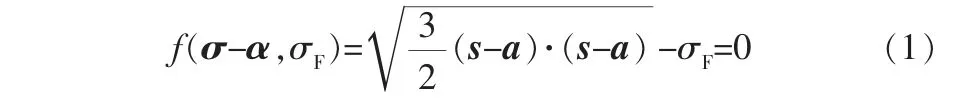
式中 a——偏背應力張量；

s——偏應力張量；

α——背應力張量，表示屈服面的中心；

σ——應力張量；

σF——摩擦應力，表示屈服面的半徑。

根據廣義正交性假定，塑性流動增量的方向為屈服面的法線方向，塑性應變增量dεp為：

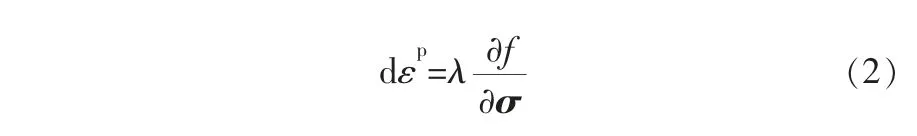
其中，?f/?σ表示屈服面的法線方向；λ為塑性乘子。

Chaboche隨動強化率認為式（1）中的總背應力α可以劃分為多個分背應力αi， 每個分量都符合Armstrong隨動強化率，即：

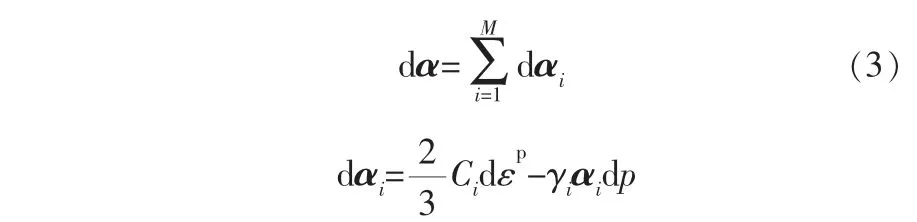
其中，M為背應力級數；Ci和γi為材料參數；p為累積塑性應變。

式（1）中的摩擦應力σF通常采用Voce單級同性硬化率描述，即：

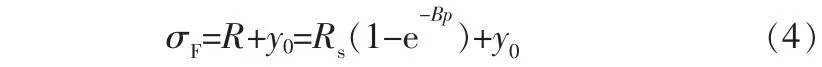
其中，R表示各向同性應力；y0表示初始屈服應力；Rs表示R能夠達到的最大值；B表示R達到穩定的速度。

大量研究表明： 上述Chaboche模型的模擬準確性很大程度上取決于參數（Ci，γi，Rs，B）的精確性。 但由于Chaboche模型具有參數多、 各參數之間關系復雜且相互制約等特征，模型參數和應力應變之間是一個非常復雜的非線性函數關系。 采用傳統方法（試驗法結合試錯法）求解上述參數，往往因背應力分段不明確、試驗數據分散性大等原因，導致模擬結果出現較大誤差［16］。

近年來， 遺傳算法被應用于確定Chaboche模型參數。 通過選擇、交叉及變異等一系列操作對模型參數進行迭代進化，從而達到提高參數求解精度的目的。 基于遺傳算法優化Chaboche模型參數可歸結為以下3個步驟：

a. 確定參數初值。 首先采用試驗法求得Chaboche模型參數初值。 參考文獻［17］，隨動硬化參數（Ci，γi）取值范圍一般服從依次減小的規律（C1>C2>C3>Ci，γ1>γ2>γ3＞γi），同性硬化參數Rs取值范圍可根據材料循環軟化/硬化特性進行判斷，b取值一般為負。

b. 適應度判斷。綜合模擬效果和計算效率選擇合適的Chaboche模型適應度函數， 即模型模擬值（εmodel，σmodel）和試驗值（εexp，σexp）的加權差值，差值越小代表參數求解越精確。

c. 進化操作。 在步驟b的基礎上，通過選擇、交叉、 變異操作， 誕生出新一代Chaboche模型參數。 重復步驟b、c，直到模型參數收斂到規定精度為止。

采用遺傳算法確定Chaboche模型參數的流程如圖1所示。

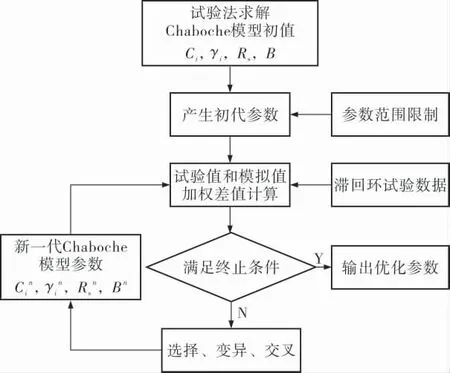
圖1 確定Chaboche模型參數的遺傳算法流程框圖

1.2 基于Chaboche模型的疲勞壽命預測方法

基于Chaboche模型預測轉子輪盤疲勞壽命的方法主要可歸納為：采用局部應力應變近似計算公式聯立Chaboche模型， 將作用在轉子輪盤的載荷轉化為輪盤危險部位（如輪槽齒根）的局部應力、應變；考慮平均應力動態松弛行為，同時結合平均應力修正模型，進行輪盤危險部位的損傷計算；最終通過損傷累計來預測輪盤疲勞壽命。 上述壽命預測流程如圖2所示（圖中的SWT模型、統一法引用文獻［18，19］）。

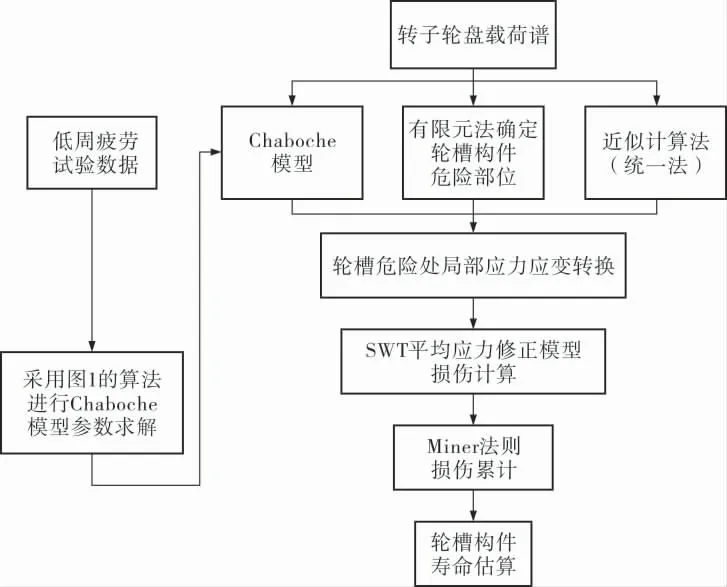
圖2 基于Chaboche模型的輪槽構件疲勞壽命預測流程框圖

2 試驗過程

2.1 光滑試樣低周疲勞試驗

為了確定Chaboche模型參數，開展了某型輪槽材料的光滑試樣單調拉伸試驗和應變比為0的應變控制低周疲勞試驗。 試驗參考相關標準［20］，在MTS-810電液伺服疲勞試驗機上進行。 該輪盤材料的低周疲勞力學性能參數如下：

屈服強度σy700 MPa

疲勞強度系數σf′ 1 051 MPa

材料彈性模量E 203 GPa

疲勞延性系數εf′ 0.205 1

強度系數K 1 024 MPa

疲勞強度指數b－0.072

應變硬化指數n 0.058 9

疲勞指數c－0.588

2.2 輪槽構件低周疲勞試驗

為了驗證基于Chaboche模型的轉子輪盤疲勞壽命預測方法的準確性，開展了脈動載荷下某型輪槽構件的低周疲勞試驗。 圖3是該輪槽構件的主要幾何尺寸，其中輪槽齒根A、B、C的理論應力集中系數Kt采用有限元法確定， 分別為3.39，3.11，2.39。

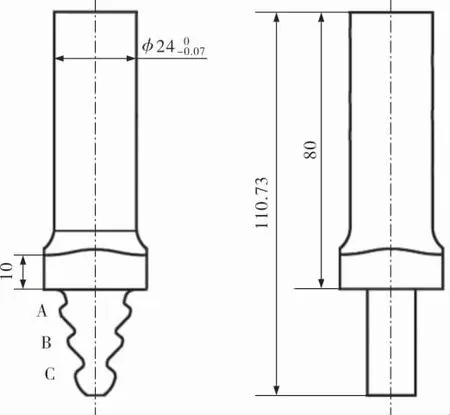
圖3 輪槽模擬件幾何形狀

輪槽構件的疲勞試驗在MTS-810電液伺服疲勞試驗機上進行， 試驗采用應力比為0的軸向載荷控制，正弦波加載。 試驗過程中采用長距離顯微測試系統實時監測裂紋長度，試驗現場與輪槽構件裂紋的測量結果如圖4所示。 記輪槽缺口部位出現長度為0.5 mm裂紋的循環周次為裂紋萌生壽命。

圖4 試驗現場與輪槽構件裂紋測量

3 某型輪槽構件的疲勞壽命預測與試驗驗證

采用基于Chaboche模型結合遺傳算法的轉子輪盤疲勞壽命預測方法（圖2），對某型輪槽構件進行了疲勞壽命預測， 并將預測結果與試驗結果進行比較。

3.1 Chaboche模型參數確定

確定Chaboche模型（式（4））中的R。 參考文獻［21］中的方法，通過試驗數據提取摩擦應力。 圖5為某典型應變幅下輪槽材料最初1/4循環（單調拉伸階段）和后續疲勞循環的摩擦應力擬合曲線。

圖5 輪槽材料的摩擦應力擬合曲線

從圖5可以看出：在最初1/4循環，當累計塑性應變增加到0.02時，摩擦應力從700 MPa迅速衰減到460 MPa，之后在循環載荷作用下呈現緩慢減小特征。采用疊加的Voce模型［22］，分別對上述兩個階段摩擦應力（σF）進行擬合，其表達式可寫成：

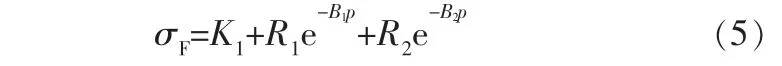
其中，K1、R1、B1、R2和B2為擬合參數。

確定Chaboche模型中的隨動硬化參數（Ci，γi）則參考文獻［23］中的方法。 為了保證精度，本次研究將背應力劃分為8級，如圖6所示。 其中，第1、2級背應力描述小應變階段，第3～5級背應力描述中應變階段，第6～8級背應力描述大應變階段。

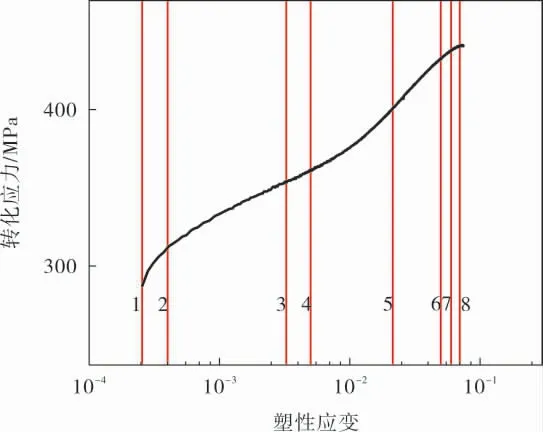
圖6 8級背應力的劃分

輪槽材料的隨動硬化參數初值列于表1中。

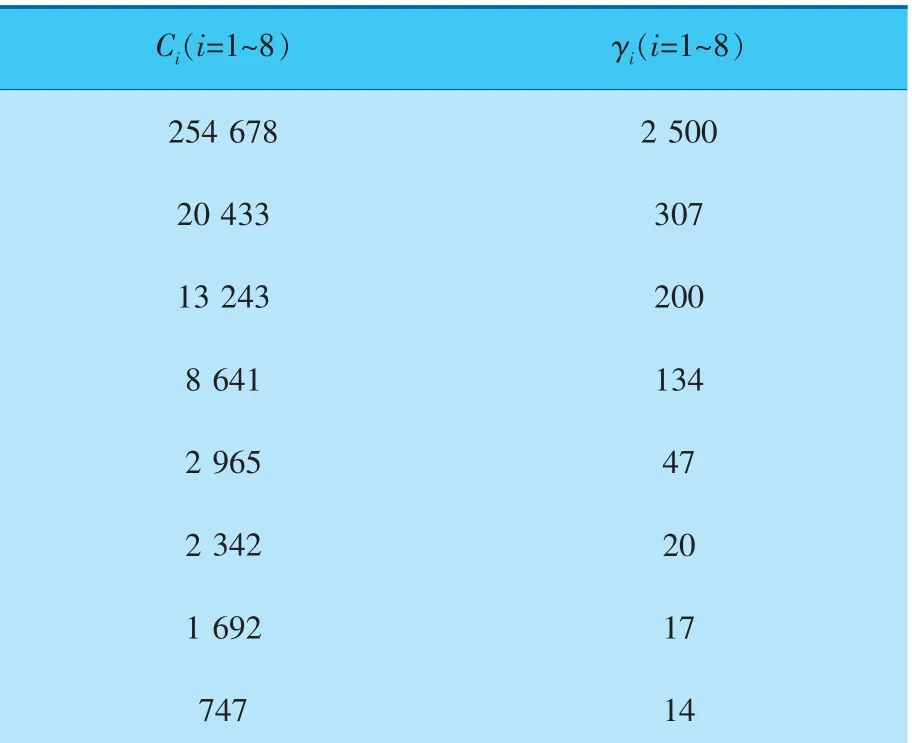
表1 Chaboche模型參數初值

前4個階段的各向同性硬化參數初值R1=287、B1=293、R2=287、B2=239、K1=465、R3=321、B3=375、R4=50、B4=2、K2=416。

采用圖1中的遺傳算法流程， 結合2.1小節中材料低周疲勞試驗結果， 可進一步優化Chaboche模型中的26個參數。 本次算法參數設置基于Matlab的Optimtool遺傳算法工具箱， 自行編寫了適應度函數。 采用二進制編碼，初始種群數量根據變量數（26個）選為300。 根據初值大小設置參數范圍限制以加快收斂速度。 為保證8個背應力分量充分發揮作用，本算法選用應變幅1.2%的滯回環數據，試驗數據選取前10個滯回環。 其中，誤差函數按下式計算：

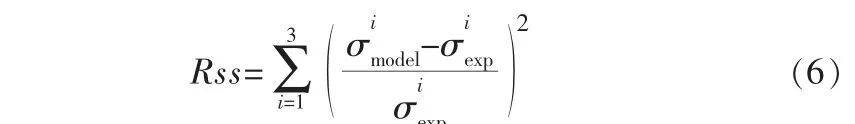
其中，σ1表示峰值應力，σ2表示谷值應力，σ3表示平均應力。

式（6）由3個分誤差函數組成，平均應力誤差用來保證平均應力的模擬精度，峰值/谷值應力誤差則控制滯回環的形狀。

采用排名選擇法， 交叉操作采用單點交叉，交叉概率定為0.5，變異概率定為0.02。 終止條件定為進化到2 000代或誤差小于0.000 01。

經過上述遺傳算法優化的輪槽材料的隨動硬化參數列于表2。

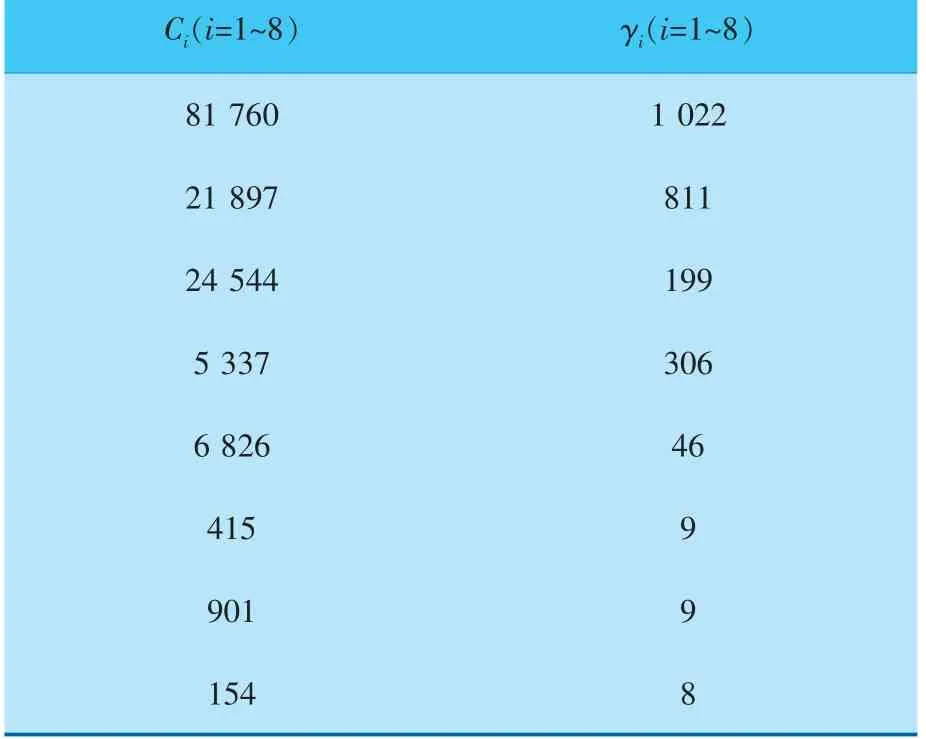
表2 Chaboche模型優化后參數

前4個階段的各向同性硬化參數優化后數值R1=261、B1=253、R2=261、B2=207、K1=458、R3=38、B3=1.88、R4=-5.2、B4=-0.355、K2=460。

3.2 輪槽材料的平均應力松弛行為模擬

為了驗證Chaboche模型描述輪槽材料循環本構關系的精確性， 采用表2中優化后的本構模型參數對輪盤材料的循環滯回環進行了模擬。 圖7給出了前10個滯回環的模擬值和試驗值的比較。可以看出，采用遺傳算法優化Chaboche模型參數能很好地模擬不同應變幅下最初1/4循環和后續滯回環形狀（包括峰值/谷值應力的演化趨勢和滯回環彈塑性過渡階段）。

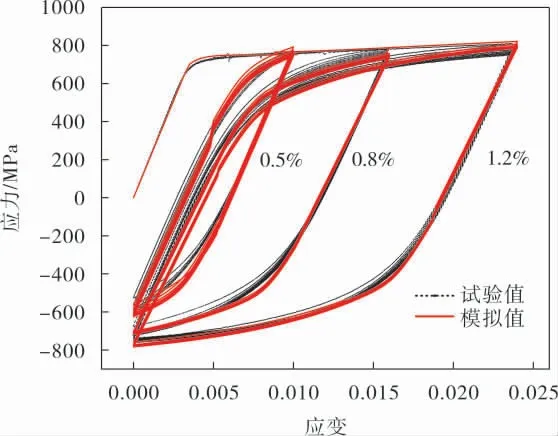
圖7 不同應變幅下滯回環模擬值與試驗值的比較

為了進一步驗證Chaboche模型模擬平均應力松弛行為的精度，采用優化后的本構模型參數計算不同應變幅下的平均應力，并與試驗值進行比較，結果如圖8所示。 由圖8可知：在各種應變幅下，平均應力均發生了明顯的松弛，應變幅越大，初始平均應力越小，而松弛速率越大。 從圖8中還可以得出： 采用優化參數的Chaboche模型總體能夠準確預測較寬應變幅范圍（0.4%～1.0%）的輪槽材料平均應力松弛行為。

圖8 不同應變幅下平均應力松弛模擬值與試驗值的比較

3.3 輪槽構件疲勞壽命預測

表3給出了基于8級背應力Chaboche模型的輪槽構件疲勞壽命模擬值、 試驗值及其相對誤差。圖9是疲勞壽命預測值與試驗值的比較。

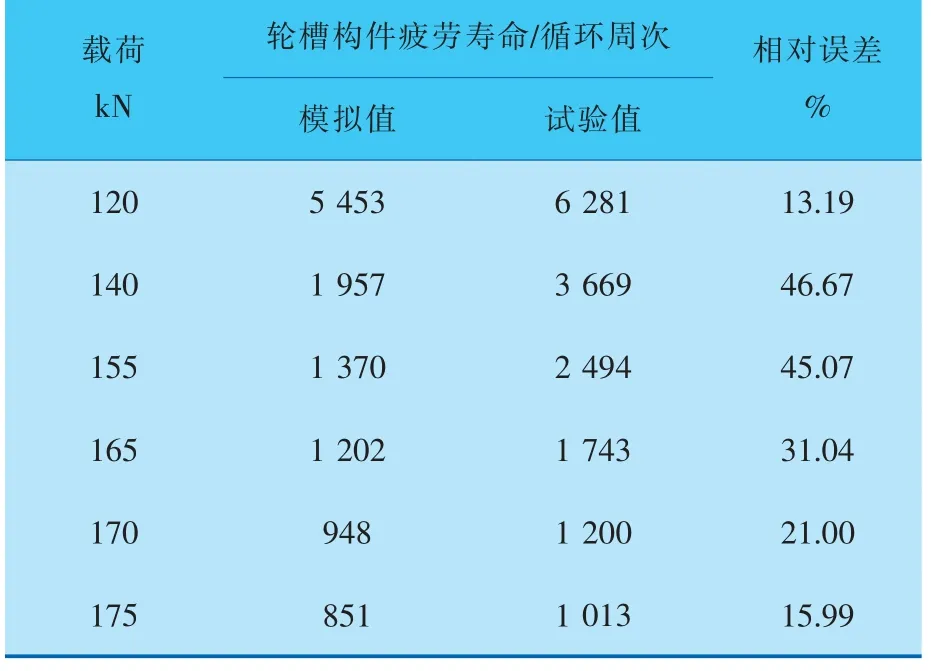
表3 輪槽構件疲勞壽命模擬值與試驗值

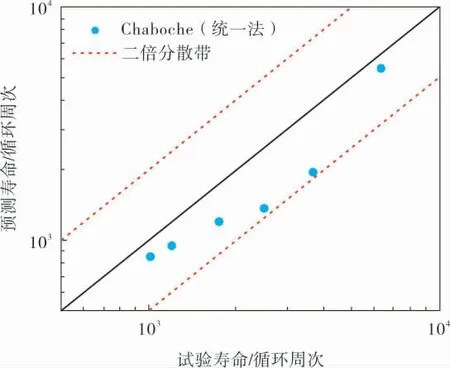
圖9 輪槽構件疲勞壽命預測值與試驗值的比較

從圖9可以看出， 基于8級背應力Chaboche模型的轉子輪盤疲勞壽命預測方法總體能夠獲得與試驗壽命較為一致的結果，在本文研究的載荷條件下， 預測壽命與試驗壽命在二倍分散帶之內。

4 結論

4.1 基于局部應變法， 采用遺傳算法優化Chaboche模型參數， 建立起一種預測轉子輪盤疲勞壽命的新方法。

4.2 采用參數優化的Chaboche模型模擬了某型輪盤材料在多種應變幅下的滯回環形狀和平均應力松弛行為，通過與試驗值相比較證明了兩者一致性較好。

4.3 采用筆者建立的轉子輪盤疲勞壽命預測方法對某型輪槽構件開展了疲勞裂紋萌生壽命預測。 通過與試驗結果的比較可知，兩者誤差在二倍分散帶之內。