最大水平主應力評價方法對比研究

張洋洋 劉志慧 鄭黎明 李成華

（1.中國石油大學（華東）石油工程學院；2.燕山大學車輛與能源學院）

在油氣田開發過程中，最大水平主應力的數值隨開采深度逐漸變化，內地質動力作用或外地質動力作用推動著巖石組分、外圍環境等發生變化。 無論是通過測定地應力來研究區域應力場分布，判別地層的穩定性，還是判別三維地應力的大小，推斷正、逆、滑移斷層的發生情況，反演構造歷史變化，最大水平主應力的準確計算都扮演著重要作用。

通過統計國內外多個樣本點的應力計算值，建立最大水平主應力與孔隙壓力、上覆巖層壓力和最小水平主應力之間的相互關系，可以方便現場快速得到最大水平主應力的數值，進行礦場應力場模擬，為現場實際應用提供有益指導。

1 最大水平主應力研究方法

1.1 經驗或理論公式

與深度相關的線性函數是應用最多的統計公式形式，具體如下：

式中 A、B——統計擬合系數；

H——地層深度；

σH——最大水平主應力。

劉江等給出了大慶油田部分區塊的最大水平主應力σH計算公式［1］：

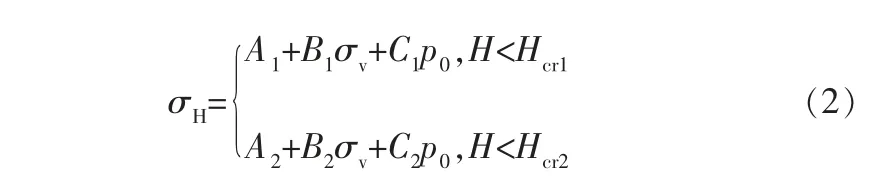
式中 Ai、Bi、Ci——統計擬合系數；

H——地層深度；

Hcri——統計的某一臨界地層深度；

p0——孔隙壓力；

σv——上覆巖層壓力。

1.2 水壓致裂

水壓致裂地應力測量法可分為水力壓裂法、套筒壓裂法和預存裂隙水壓致裂試驗法［2］。 水壓致裂對于常規地質部門、 公司而言成本較高，但在油氣藏開發過程中，尤其是低滲透地層，是一項常規作業。

對裸眼井水力壓裂地應力測試而言，計算獲得的最大水平地應力精度依賴于計算公式。 應用較多的模型由Haimsons提出， 考慮了壓裂液向地層中的滲濾［3］，即：

式中 pb——地層破裂壓力；

p0——孔隙壓力；

T——地層名義抗拉強度；

α——Biot系數；

ν——泊松比；

σh——最小水平主應力。

實際礦場操作中，為了簡化計算，通常采用Hubert和Willis（1957）提出的公式，利用裂縫瞬時閉合壓力、裂縫重新張開壓力和孔隙壓力進行計算［4］：

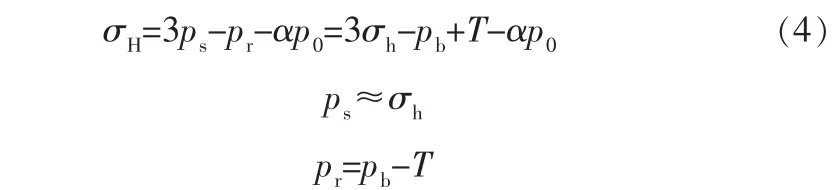
式中 p0——孔隙壓力；

pb——井下臨界破裂壓力；

pr——裂縫重新張開的壓力；

ps——裂縫的瞬時閉合壓力；

T——巖石抗拉（張）強度；

α——Biot系數，α=1；

σh——最小水平主應力。

1.3 試驗測量方法

常用的試驗測量方法包括聲發射法和應力恢復法。

聲發射法即凱瑟效應法， 基于巖石材料的“凱瑟效應”和“抹錄不凈現象”來測定巖體地應力［5］。 該方法測定現今地應力可靠性相對較低。

應力恢復法需要測量多個應力分量，對巖心切割多個扁槽。 目前應力恢復法已很少被應用于地應力測量，但在礦山中仍被作為監測礦柱和圍巖應力變化的一種方法。

1.4 鉆孔崩落法

Zoback M D等推導得到利用崩落寬度計算最大水平主應力σH的表達式［6］：

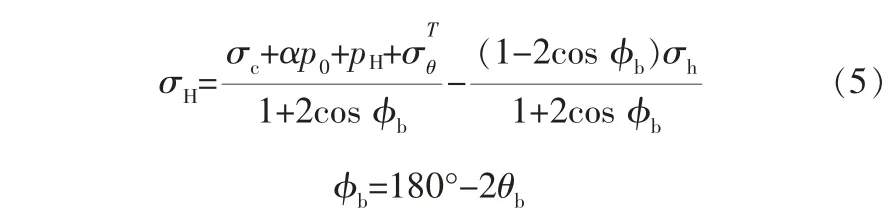
式中 p0——孔隙壓力；

pH——井筒液柱壓力；

α——Biot系數；

θb——起始崩落方向與最大水平主應力的夾角；

σc——井壁起始崩落的臨界應力；

σTθ———溫度應力；

φb——井壁崩落寬度（井壁崩落邊緣的夾角）。

基于線彈性理論，王從樂等確立了井壁首次坍塌時最大水平主應力σH與井眼崩落寬度φb、巖石強度（內聚力和內摩擦角）、地層壓力之間的數學模型［7］：

式中 C——內聚力；

p0——孔隙壓力；

pH——井筒液柱壓力；

α——Biot系數；

φ——巖石內摩擦角。

1.5 應力差方程聯立

當井眼假設不存在崩落時，Sinha B K等針對聲波測量預測水平應力開展了大量研究，利用交叉偶極子測井得到的三維剪切模量［8］。 假設有效主應力與三維剪切模量的相對變化是線性相關的，即：

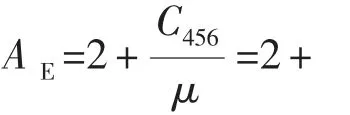
2 最大水平主應力評價方法對比

經驗或理論公式盡管具有計算簡單、快捷的特點，但是區域針對性強，可靠性低，不易于推廣；水壓致裂方法適用范圍較廣，可適用于不同井深， 能夠充分利用油田豐富的水力壓裂資料，并且簡單方便，對于部分高滲或存在較大塑性應變的地層可能無法獲得資料；試驗測量方法只能反映近井帶局部區域狀態，巖心獲取受限，受應力集中的影響較強； 鉆孔崩落法計算方法復雜，需要在下套管前多臂井徑測量，在無崩落或非均質時不適用；應力差方程聯立在現場進行偶極子測井相對較少，利用該方法獲得最大水平主應力受到一定限制。

綜合對比分析各種方法后發現，油氣田開發過程中，實用性更為廣泛、優點更為明顯的是水壓致裂方法。

3 最大水平主應力計算公式

計算最大水平主應力時需要的部分參數可能較難獲取，當實際地層橫向或縱向非均質變化較強時，地應力存在更為明顯的差異，數據來源和結果可靠性可能會進一步降低。

統計國內外應力測量數據之后發現，最大水平主應力在不同區域數值差異懸殊；利用簡單的地應力計算，對于分析較廣區域或平面非均質較強區域的具體地應力分布是不合適的。

統計萬福勘探區、元壩某井、四川省大涼山腹地、Norwegian Sea等國內外關于最大水平主應力測量的相關數據，考慮上覆巖層壓力、孔隙壓力和最小水平主應力這3個相對較易獲得的參數，對數據進行擬合，得到關于最大水平主應力與孔隙壓力、上覆巖層壓力和最小水平主應力的數值關系模型；該模型有利于增加計算公式的普適性，降低數據獲取難度。

擬合公式中引入最大和最小水平主應力比值、側壓系數等概念，以說明水平主應力受垂向、大地構造等的影響， 如表1中σh/（σv-p0） 為假設Biot系數α=1時反映斷裂的有效最小水平側壓系數，σH/σh為最大和最小水平主應力的比值。 變量擬合時常用對數擬合、線性擬合、指數擬合方式，對表1涉及的變量1-（σv-np0）/σh與σH/σh-1進行不同形式的擬合，且給出擬合度。 發現當孔隙壓力倍數n=1時，利用前述常用壓力、應力參數計算最大水平主應力具有更高的可行性，且采用對數擬合的擬合精度更高。 同時對數擬合模型計算簡單，有利于提高現場基礎數據的獲取簡便性。 n=1時σv-p0表征巖石有效應力（該有效應力在大量研究人員提出破裂壓力簡易計算模型中常見），能夠同時涵蓋縱向有效應力與水平構造應力對最大水平主應力的協同影響。

表1 1-（σv-np0）/σh與σH/σh-1的不同類型曲線擬合度

進一步地，在雙對數坐標下利用對數擬合形式繪制數據，如圖1所示，發現擬合數據趨于雙曲型變化規律， 且在橫軸與縱軸分別向趨于數值0的方向集中。

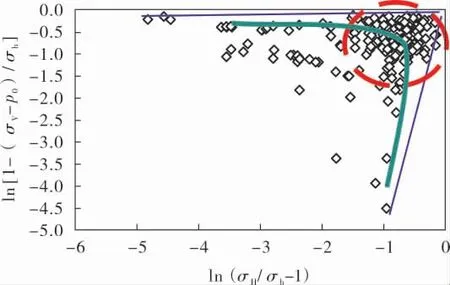
圖1 ln［1-（σv-p0）/σh］與ln（σH/σh-1）的關系圖

筆者對圖1所示的雙曲型曲線進行分析，進而得出了一種最大水平主應力的簡便計算公式：

4 結論

4.1 闡述了最大水平主應力的預測方法，并對各種方法的工作特點加以綜合運用，對各方法的特點和局限性進行了總結分析，綜合比較后認為各種方法中，水力壓裂方法在計算時更為適用。

4.2 最大水平主應力計算時需要的部分參數可能較難獲取，當實際地層橫向或縱向非均質變化較強時，地應力存在更為明顯的差異，數據來源和結果可靠性可能會進一步降低。

4.3 結合國內外相關測量數據，利用反映裂縫的有效最小水平側壓系數的倒數、最大和最小水平主應力的比值，得到了新的統計公式σH=5.137σh－7.874（σv-p0），為油氣田現場實際應用提供了有益指導。