剪力柔性梁格法在π梁斜拉橋中的應用研究
宋文鋒,龐芝炯
(重慶中煤科工工程技術咨詢有限公司,重慶 400042)
0 引言
有限元法是目前應用最廣的斜拉橋分析方法,且具有計算方便快捷、精度較高,同時可以與規范銜接,因此可滿足橋梁結構的力學行為分析研究。由于不同的有限元建模方法有不同的特點,因此在利用有限元方法對斜拉橋結構進行力學行為分析時,需要根據精度和需要解決的問題選擇模型離散。結構有限元建模一般分為以下四種方法:單梁法、梁格法、板殼單元法和三維實體單元法。梁單元法無法得到內力的橫向分布,板殼元法和實體元法模型復雜,計算費用高,數據處理煩瑣;梁格法因其計算方便、費用經濟,在工程分析中廣泛應用。
1 梁格理論
1.1 梁格法
梁格法是E.c.Hambly[1]提出的一種簡便實用的分析方法,把復雜結構模擬成一個縱、橫交叉的空間梁格體系,其力學模型符合結構的實際受力情況,可以直接得到結構的內力與變形,即考慮了荷載作用下結構沿縱向產生的彎曲和整體扭轉,還考慮了整個截面的橫向變形,為斜拉橋π梁結構分析計算提供了一種較實用的理論方法。
1.2 梁格法基本原理
將實際結構的剛度(如抗扭剛度和彎曲剛度等)用梁格剛度等效代替,在相同荷載下撓曲線相同,因兩者結構特性上的差異,等效梁格的內力近似等效實際結構的內力[2]。梁格法建模的關鍵:
1)等效梁格與實際結構縱向彎曲等效,橫向梁格中性軸與實際結構同一高度。
2)梁格剛度與實際結構剛度等效,同時對縱、橫向梁格的剪切面積和抗扭慣性矩進行修正。
π梁斷面采用雙縱梁式模型,在梁格力學模型簡化時,邊梁的面積和抗彎剛度與實際結構等效性,且豎向抗彎剛度提供的約束扭轉剛度與實際結構等效性[3]。
2 工程概況
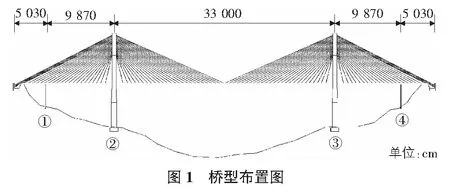
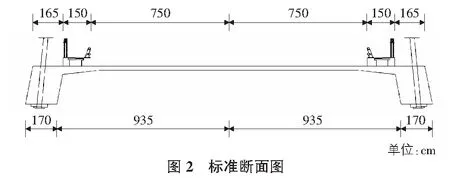
某特大橋橋跨布置為(149+330+149) m浮體系PC斜拉橋,邊跨距索塔中心線98.7 m處設置輔助墩如圖1所示,主梁采用C50預應力混凝土π梁,梁高2.3 m,板厚0.25 m,縱肋底部寬1.7 m,梁頂部全寬21.3 m,底部全寬22.1 m,每6 m設置一道0.25 m的橫隔梁;索塔為倒Y型,采用C40鋼筋混凝土及預應力鋼筋混凝土箱形截面,塔高121.5 m,其中上塔柱高33 m、下塔柱高55.5 m、中塔柱高33 m;斜拉索采用扇形布置,共計212根,邊跨與中跨各設52對拉索,除邊跨最外端4對拉索間距為0.7 m外,其余斜拉索索距均為6 m,同時在塔中設置了1對外拉索,斜拉索采用φ7鍍鋅鋼絲,標準強度1 600 MPa;橋面寬:1.5 m人行道+15 m車行道+1.5 m人行道=18.0 m,如圖2所示。大橋設計荷載為汽車-超20級、掛車-120,人群-3.5 kN/m2。
3 撓度、應變控制截面測點布置
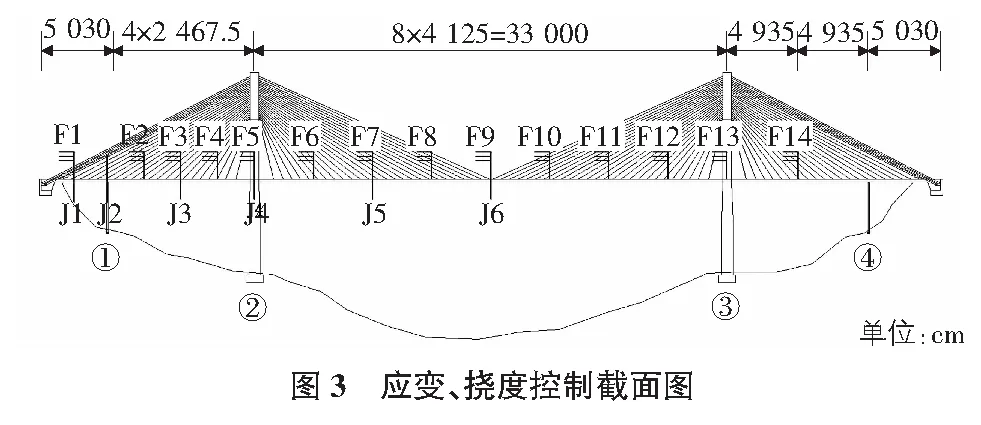
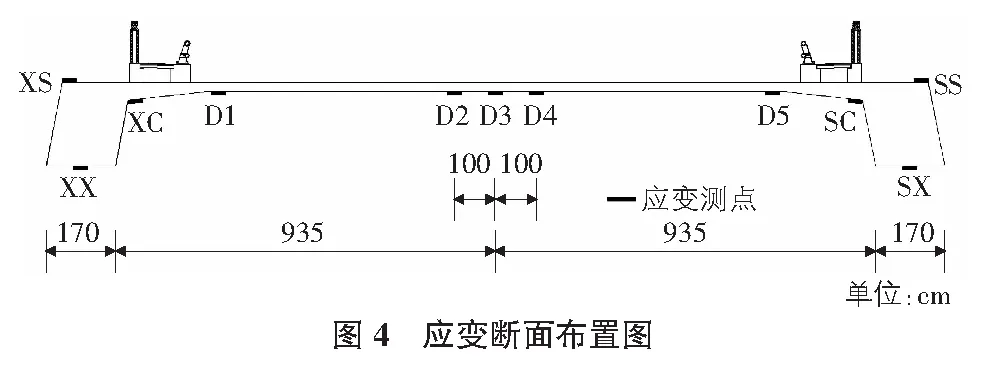
根據斜拉橋的受力特點確定橋梁的內力和撓度控制截面,通過控制截面的實測值以驗證剪力柔性梁格法計算分析斜拉橋的準確性,實用性。應變控制截面劃分如下:左側邊跨跨中截面J1、輔助墩中心1.4 m截面J2、次邊跨跨中截面J3、主塔中心截面J4、主跨L/4截面J5、主跨跨中截面J6;撓度控制截面為F1~F14,如圖3所示,控制截面的斷面布置如圖4所示。
4 結構有限元模型
為了驗證剪力柔性梁格法的雙縱梁應用在π梁斜拉橋上的精確程度,梁格法模擬如下:
1)縱橫向梁格:將π梁對中劃分近似實現“共同中性軸”的縱向梁格,并在每個節段交界處設置虛擬橫梁,同時對在0號塊處和橋臺處應加密梁格。
2)索塔采用空間梁單元,截面與實際索塔截面相同,且索塔橫梁采用共節點或剛性連接模擬。
3)斜拉索采用只承受拉的桁架單元模擬,拉索與主梁及主塔均采用剛性連接[4]。
4)邊界條件:索塔、輔助墩采用一般支承中的固結模擬,橋臺處4個盆式支座,采用一般支承模擬,主塔及輔助墩處2個盆式受壓支座采用彈性連接。
根據以上梁格模擬原則,依托工程采用空間有限元分析軟件Midas Civil建立全橋結構有限元模型如圖5所示,主梁采用雙縱梁梁格模型,其中836個縱梁單元和419個橫梁單元;斜拉索采用受拉桁架單元,共212個;索塔和輔助墩采用梁單元,共160個。

5 理論與實測結果分析
根據控制截面的彎矩等效及內力影響線布載的原則,確定試驗荷載,全橋共設6個工況,分別為J1,J2,J3,J4,J5,J6,以驗證結構有限元模型的準確性。
5.1 主梁應力對比分析
在試驗荷載作用下實測π梁的應變,并根據彈性模量將應變轉換為應力,同時對實測值與理論值進行分析對比,以驗證剪力柔性梁格法計算π梁斜拉橋的精確性及實用性。各工況試驗荷載作用下的應力增量如表1所示。
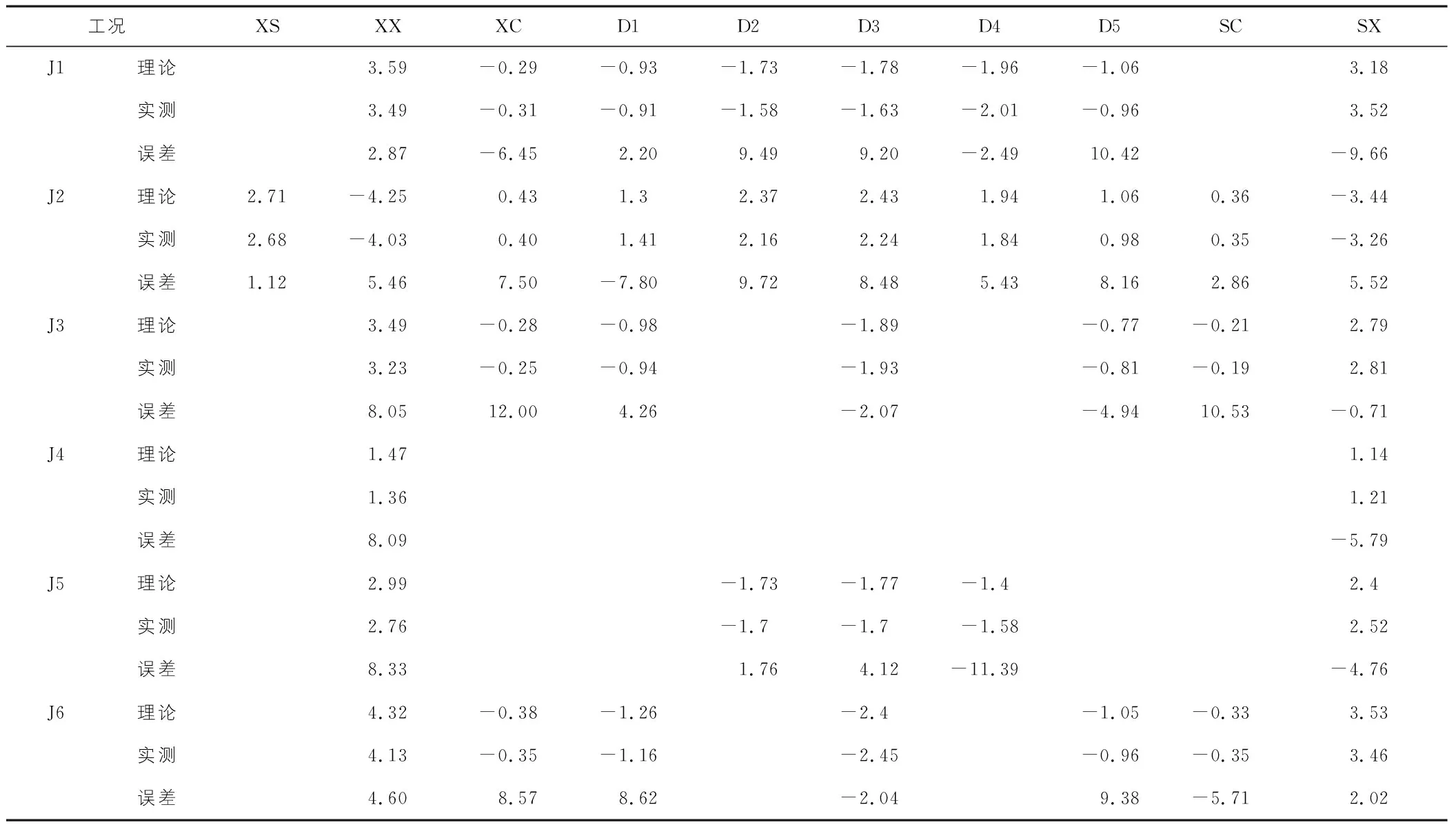
表1 試驗荷載作用下混凝土應力 MPa
通過以上對比分析可知:梁格模型的計算結果可以準確地反映出試驗荷載作用下斜拉橋π梁的正應力分布,且理論較接近實測值,最大誤差僅11.39%,同時也驗證了雙縱梁模型影響線的準確性及可靠性。
5.2 主梁撓度分析
在試驗荷載作用下對π梁撓度的實測值與理論值進行分析對比,也是驗證剪力柔性梁格法精確與否的最基本原則之一。各工況試驗荷載作用下的撓度增量見表2。
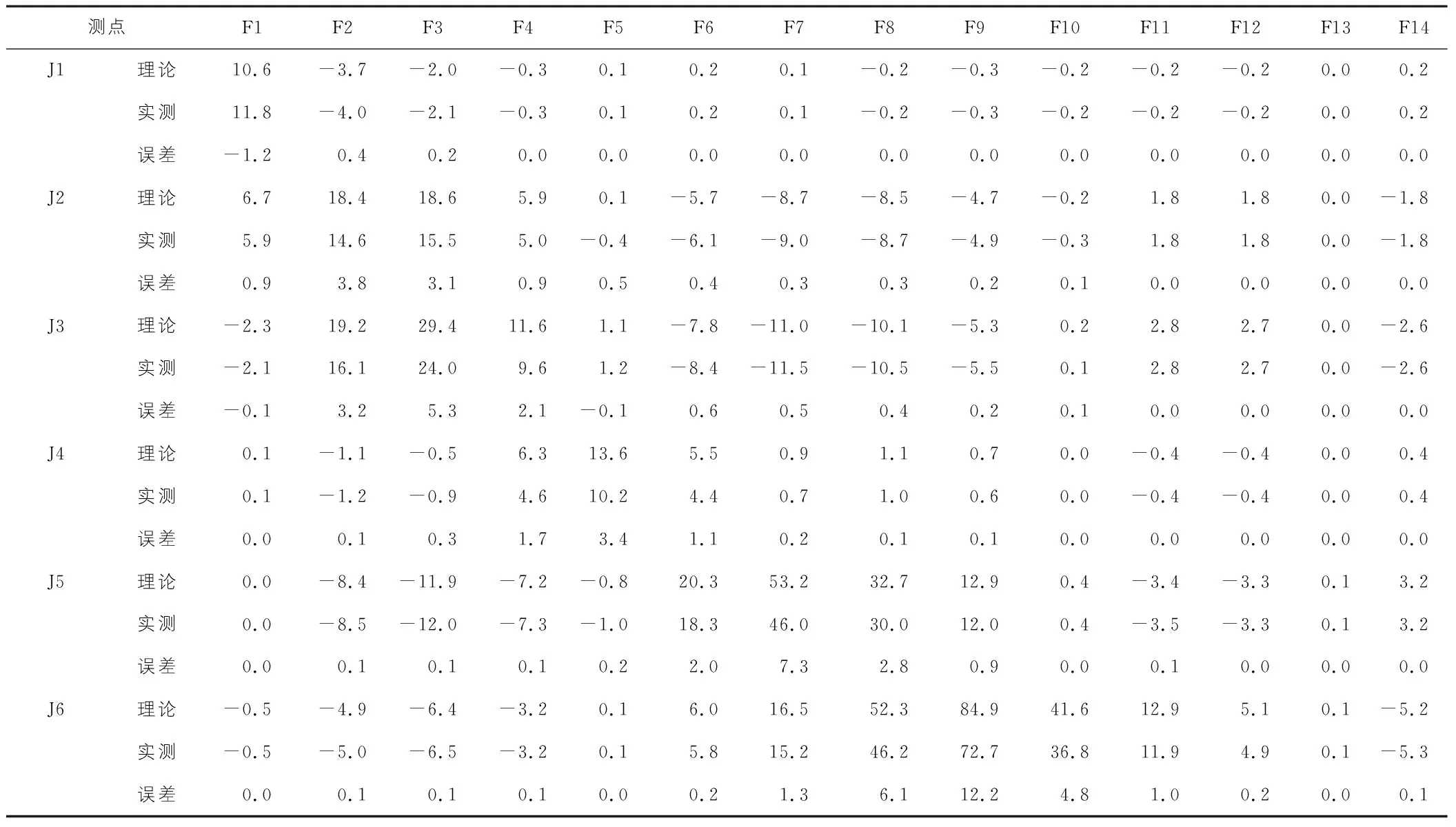
表2 試驗荷載作用下橋梁撓度 mm
通過以上撓度對比分析可知:雙縱梁梁格模型的計算結果可以準確地反映出試驗荷載作用下斜拉橋π梁的撓度變化,且理論較接近實測值,最大誤差僅12.2 mm,驗證了剪力柔性梁格法在π梁斜拉橋計算中的合理性,為同類斜拉橋的結構力學行為分析提供借鑒[5]。
6 結語
通過剪力柔性梁格法對依托工程進行有限元結構分析,并根據控制截面彎矩等效及內力影響線布載的原則,確定試驗荷載,最后通過試驗荷載作用下的理論值與實測值進行分析對比,得出如下結論:
1)雙縱梁梁格模型的計算結果可以準確地反映出試驗荷載作用下斜拉橋π梁的正應力分布及撓度變化,且理論較接近實測值,應力最大誤差僅11.39%,撓度最大誤差僅12.2 mm。
2)π梁對中劃分近似實現“共同中性軸”的縱梁及每個節段交界處設置虛擬橫梁的梁格模型可滿足π梁斜拉橋受力分析的工程精度要求。
3)雙縱梁結構的內力影響線與依托工程的結構內力影響線基本相符。
4)剪力柔性梁格法的雙縱梁模型可以準確地把握π梁斜拉橋的力學行為,計算結果安全可靠,為類似π梁斜拉橋結構的力學行為分析提供參考。

