基于遙感數據的不確定性的農業水資源優化配置研究
——以漳河灌區為例

趙金淼 佟 玲* 岳 瓊 鄭 靜 黃 鑫 李 鵬

(1. 中國農業大學 中國農業水問題研究中心，北京 100083；2. 湖北省漳河工程管理局，湖北 荊門 448156)

在全球經濟快速發展和人口不斷增長的背景下，持續增長的用水需求與有限水資源之間的矛盾日益突出。我國是農業大國，農業作為最大的用水主體，面臨著前所未有的用水挑戰。據我國水資源公報統計，我國2020年農業用水量為3 612.4 億m3，占總用水量的62.1%，耕地實際灌溉畝均用水量356 m3；而我國人均水資源占有量僅為世界平均水平的1/4，農田灌溉水有效利用系數僅為0.565[1]。農業水資源供需不匹配、利用效率低及時空分布不均等問題嚴重制約了我國農業可持續發展。合理的用水策略可以節約35%的水和能源[2]。灌區是灌溉農業生產的重要載體[3]，探究灌區供需水空間分布，實行更科學有效的水資源分配與管理[4]，對提高水資源的利用效率、緩解水資源供需矛盾以及保障糧食生產安全具有重要意義。

農業水資源優化配置是結構復雜的大系統優化措施，具有多尺度、多層次、多階段、多變量和非線性等特點[5]。在開展水資源優化配置，降雨量作為基本參數時，具有很強的時空變異性，增加了建模的難度。遙感技術的利用和地理信息系統的發展使獲取更多空間信息成為可能[6-7]，充分利用遙感信息開展更精準的農業水資源空間分布研究是當前熱點。

由于水資源配置過程中存在著管理、水文氣象和作物價格等諸多不確定性因素，針對農業水資源優化配置系統中的不確定性問題，隨機數學規劃、區間參數規劃和模糊數學規劃等不確定性方法已被廣泛應用于研究農業水資源優化配置系統中的不確定性[8]。農業水資源優化配置系統中的降雨量、水價和種植面積等系統參數可能更復雜，單一因素的不確定性方法很難量化其特征。例如，水價、懲罰系數等參數具有模糊特征，采用模糊數能夠更好的表示其變化范圍和中間趨勢。然而在大多情況下，很難獲得這些參數確定的模糊隸屬度函數，而將帶有上下邊界的區間數引入到模糊隸屬度函數中，構成模糊區間隸屬度函數能夠很好地解決水資源優化配置系統中的不確定性問題。張帆等[9]將這模糊區間隸屬度函數的模糊區間集引入到灌溉水分配模型，用來處理水資源優化配置模型中的雙重不確定性參數。在實際灌溉中，優化目標和約束條件作為水資源優化配置系統中基礎構件，往往需要考慮存在于優化目標和約束條件雙側的模糊區間參數。同時，風險是由水資源優化配置系統的不確定性因素引起的，水資源系統的不確定性因素必然帶來水資源優化管理的風險，需要開發反映系統不確定性和風險規避的灌溉水資源優化模型[10]。國內外目前對水資源優化的理論研究已經取得了較多的成果，如潘琦等[3]結合渠系輸水模擬和土壤水量平衡模擬構建的渠系優化配水模型，為灌區水資源管理提供指導；趙敏等[11]結合Jensen模型與土壤水平衡模型實現灌區尺度灌溉水資源優化配置；岳瓊[12]等構建區間兩階段模糊可信性約束規劃模型,實現灌區各用水戶間水資源優化配置。已有研究中的水資源優化配置系統中的降雨參數多采用以點帶面的形式，忽略降雨量的時空變異性進行水資源優化配置，結合遙感數據進行灌區水資源優化的應用研究較少。位于湖北省的漳河灌區降雨量年內分配不均勻，年際分配也不均勻，豐枯不均勻，當漳河灌區降雨不足時，需要灌溉以滿足作物生長的用水需求。因為漳河灌區曾旱情頻發，2010年秋至2014年連續5年干旱，且旱情通常伴隨著降雨強度小、時空分布不均的特點[13]，導致供需矛盾突出，因此有必要結合遙感降雨數據，針對典型枯水年進行水資源優化。

本研究以漳河灌區作為研究區域，基于灌區遙感降雨量數據，引入模糊可信性約束規劃，以同時處理系統不確定性參數和違規風險，構建全模糊區間可信性約束非線性規劃模型，得到更精細的優化管理方案，為管理者提供豐富的決策參考，助力農業水資源高效利用與精準管理。研究內容主要包括：(1)探究遙感和雨量站降雨量數據結合方式，獲取漳河灌區典型年降雨空間分布情況；(2)引入水分生產函數定量表征各時段作物產量對水分虧缺的響應；(3)引入區間數和模糊區間數分別處理模型中的單一不確定性和雙重不確定性；(4)引入模糊可信性約束規劃權衡系統效益和約束違反風險；(5)開發相應的算法，求解優化模型，生成高效的農業水資源分配方案。

1 研究區概況與基礎數據

1.1 研究區概況

漳河灌區位于我國長江流域,湖北省中部，流域范圍介于東經111°～112°，北緯30°～32°，由副壩、一干渠、二干渠、三干渠、四干渠、西干渠和總干渠等7個分灌區組成(圖1)，流域面積2 980 km2。漳河灌區內有漳河水庫，漳河水庫是由觀音寺、林家港、王家灣和雞公尖4座水庫通過3段明渠串聯而成。其中觀音寺水庫在最前端，有來水多庫容小的特點，雞公尖水庫在最末端，有來水少庫容大的特點。水庫來水情況較為復雜，從多個支流來水，出水口也不唯一。漳河水庫周圍公路較多，交通便利，漳河水庫服務著漳河灌區260多萬畝農田。

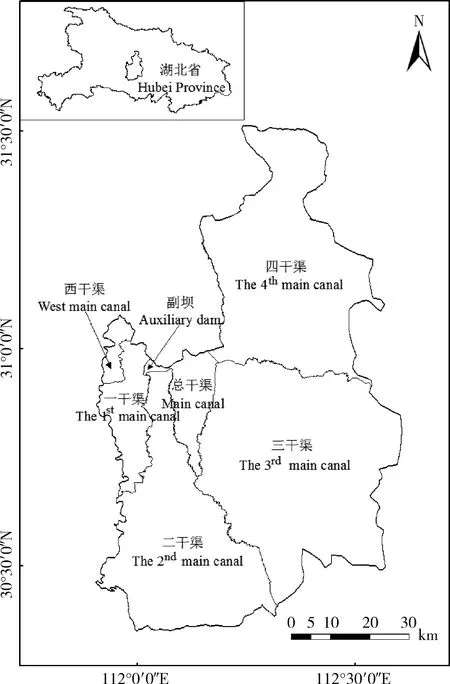
圖1 湖北省漳河灌區位置圖Fig.1 Location map of Zhanghe irrigation area,Hubei Province

漳河灌區西北偏高東南偏低，海拔高程自-4～461 m，高程空間變異性較大，屬于亞熱帶大陸性氣候。年蒸發量700～1 000 mm，月最大150 mm，月最小16.5 mm[12]。漳河水庫多年平均年降雨量969.7 mm，降雨量年內分配不均勻，年際分配也不均勻，豐枯不均勻[12]。降雨多集中在4月至9月，約占全年的70至80%。水庫徑流量還有連續多年豐、枯變化顯著的現象。漳河灌區的主要農作物是水稻、冬油菜和冬小麥。因為降雨和地下水完全可以滿足冬季油菜或冬小麥用水需求，所以水稻是主要灌溉作物。

2 模型的構建

2.1 空間降雨ULRR模型

2.1.1遙感數據集預處理

MODIS是美國NASA對地觀測系統系列遙感衛星平臺上的主要傳感器，具有36個光譜通道，每1～2 d可以獲取一次全球地表數據，其波段范圍廣，數據更新頻率快。使用投影變換、裁剪、重新采樣[14]和空間建模來處理2014—2020年5—8月GPM數據，然后在WGS-1984坐標系中刪除無效值，以獲得空間分辨率為0.1°的漳河灌區空間遙感降雨數據集。

降雨作為農業水資源管理的重要參數，具有很強的時空變異性。為進一步校正降雨數據集的準確性，本研究以2014—2020年5—8月鹽池、安棧口、溫家巷、車橋、掇刀、周集、張場、三界和四方等雨量站點生成了288個采樣序列，并收集采樣序列的降雨量和上述時段研究區域內的GPM面數據。采用ArcGIS軟件中的多值提取到點工具獲取采樣序列GPM點值，并對采樣序列的降雨量和GPM點值進行變化趨勢分析。

2.1.2線性回歸

采用一元線性回歸(ULR)方法縮小空間數據，具體方程如下:

Y=a0+a1X

(1)

式中：Y為雨量站站點降雨標準化值；X為雨量站站點GPM的標準化值；a0、a1為回歸系數。每個網格的回歸結果可以通過以下函數得到：

Yj=a0+a1Xj

(2)

式中：Yj為第j個網格的ULR結果值；Xj為第j個網格上GPM的月標準化值。

2.1.3反距離權重

采用GIS軟件計算ULR方法所得值與地面氣象站觀測結果之間的殘差,將殘差進行反距離權重插值,計算公式如下：

(3)

式中：Rj為第j個網格殘差值；Zi為第i個雨量站站點殘差值；n為雨量站站數；di為第j個網格到第i個雨量站的距離；p為距離影響因子。

2.1.4降尺度空間降雨數據集結果

各網格的最終降雨情況計算公式如下：

Pj=Yj+Rj

(4)

式中：Pj為第j個網格的降雨量結果；Yj為第j個網格的ULR結果值；Rj為第j個網格的殘差值。

2.1.5交叉驗證

分別采用GPM數據、一元線性回歸方法(ULR)、反距離權重方法(IDW)和線性回歸殘差方法(ULRR)獲取漳河灌區降水量空間分布情況，采用交叉驗證方法[15]與ULRR方法進行比較，評估ULRR方法的適用性。使用均方根誤差(RMSE)、平均絕對誤差(MAE)和平均相對誤差(MRE)作為評估不同方法的標準。這些指標的計算公式如下：

(5)

(6)

(7)

式中：Pi為第i個估計結果；Mi為第i個觀測結果；n為雨量站站點數。

2.1.6水分敏感指數處理

為了量化灌水量在不同時期對產量的影響，進而量化關鍵生育期需水權重，需要建立以各生育期供水充足程度與產量比的關系。其中用得比較多且較適合我國水稻生育規律的最普遍的形式有4種[16]，此處采用Jensen模型水分生產函數，模型結構是連乘形式。根據張帆[9,17]研究，Jensen模型各生育階段的水分敏感指數時間尺度與其他時間尺度可以通過累加原則互相轉換，可以將水分敏感指數的時間尺度統一到月尺度。

模型具體表達形式如下：

(8)

式中：j為6、7、8和9月編號；Ya為作物的實際產量，kg/hm2；Ym為最大產量，kg/hm2；ETcj為第j月的實際作物需水量,mm；Wij為第i個網格j月的實際灌水量,mm；Pij為第i個網格j月的有效降雨量，mm；bj為第j月的水分敏感指數。

基于Jensen模型和相關文獻[18-19]，Jensen模型各生育階段的水分敏感指數時間尺度與月尺度可采用下式計算：

(9)

式中：bj為第j月水分敏感指數；dt為第t個生育期包含天數；λt為第t生育期水分敏感指數；dj為j月內月內包含天數；D為生育期內每個月的天數。

2.2 基于遙感數據的不確定性農業水資源優化配置

2.2.1目標函數

為了準確反映不同生育期作物對水分的需求，最大化經濟效益，本研究建立基于作物水分生產函數的灌水量分配優化模型。據張祖蓮等人的研究[17]，Jensen模型在描述湖北省水稻生長方面被認為優于其他水分生產函數。為了更好地解決不確定的問題，根據漳河灌區的特點，本研究引入了一種基于期望值的(EVB)[18]方法來處理在模型目標和雙重約束中,以梯形模糊區間集表示的種植面積和可用供水參數；采用95%置信區間數表示作物價格、作物產量和種植面積等參數；此外，本研究希望反映與違反系統約束相關的復雜性，所以對可供水量參數采用可信性約束。因此，建立模糊區間可信性約束非線性規劃模型，解決漳河灌區灌溉用水管理中的灌水量問題：

(10)

式中：F為經濟效益，元；i為各個分灌區(i=1,2,…,7)，包含副壩、一干渠、二干渠、三干渠、四干渠、西干渠和總干渠七個分灌區；j為主要生長月份，包含5、6、7和8月；BY表示作物價格，元/kg；Ym為充分灌溉條件下作物最大產量，kg/m2；Ai為i分灌區的種植面積，m2；Wij為i分灌區j月灌水量，是決策變量，mm；Pij為i分灌區j月降雨量，mm；ETcj為j月實際作物需水量，mm；bj為j月水分敏感指數；C為種植成本，元/m2。

2.2.2約束

模型目標受到以下約束：

1)可供水量限制。

(11)

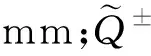
2)作物需水量限制。

(12)

(13)

式中：Wij為i分灌區j月灌水量，是決策變量，mm；Pij為i分灌區j月降雨量，mm；ε為最低需水系數，通過漳河灌區調研數據獲得；ETcj為j月實際作物需水量，mm。

3)非負性約束條件。

Wij±≥0, ?i,?j

(14)

2.2.3模型求解方法

步驟1：建立模糊區間可信性約束非線性規劃模型。

步驟2：將目標函數和約束條件中的模糊數轉化為其期望值。例如ξ的期望值被定義為[19]：

(15)

(16)

步驟4:一般來說，為了避免違反約束條件的高風險，顯著的可信度水平應大于0.5。基于步驟3，模糊區間可信性約束非線性規劃模型可以轉換為典型的區間模型，如下：

(17)

約束：

(18)

(19)

(20)

Wij±≥0, ?i,?j

(21)

步驟5：通過交互算法將區間模型分解為兩個子模型[21-22]。由于目標函數是求最大化的利益，因此應首先求解上界子模型。

步驟6：求解上界子模型，并在不同給定的可信度水平下得到相應的方案。

步驟7：根據步驟6得到的解，求解對應的下界子模型，得到相應的解。

步驟8：結合步驟6和步驟7中的解決方案，在給定的每個可信度水平下生成最終灌水量分配方案。

2.3 基礎數據

本研究對1964—2019年降雨量進行頻率分析，選擇頻率為80%的2014年為典型枯水年進行研究。本研究所使用的遙感數據來自于全球降雨測量(Global Precipitation Measurement)數據，2014年4月1日發布，空間分辨率為0.1°，時間分辨率為月。氣象數據從中國氣象數據服務中心(http:∥data.cma.cn/en)下載。通過調研和文獻[13,24]收集2003年到2018年度社會經濟資料、作物種植面積、作物產量和水文資料，如表1。通過調研獲取2014—2020年間包括鹽池、安棧口、溫家巷、車橋、掇刀、周集、張場、三界、四方、藤店等雨量站降雨量數據。通過調研獲取漳河灌區最大作物產量為11 500 kg/hm2，平均種植費用為7 000元/hm2。

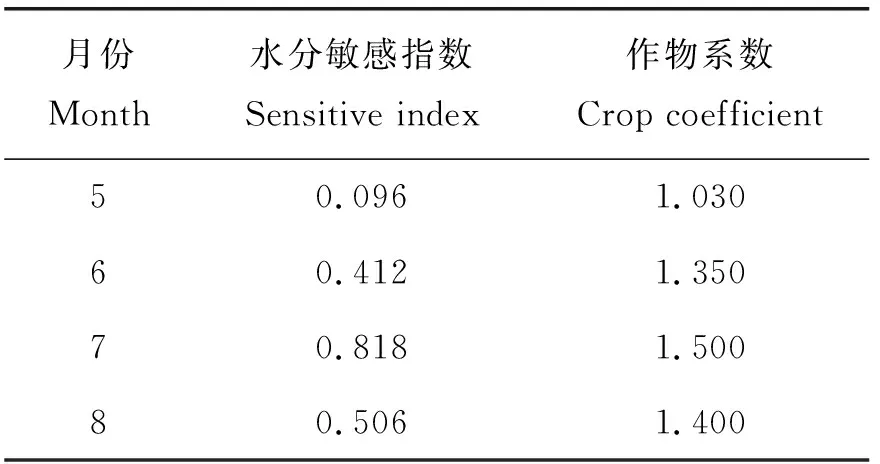
表1 漳河灌區基礎參數Table 1 Basic parameters of Zhanghe irrigation area

漳河灌區水稻各個生育期內不同月的實際作物需水量(ETc)采用作物系數法[23]確定。其中，根據灌區團林氣象站1988—2018近30年間氣象數據，采用Penman-Monteith公式計算得到1988—2018年5—8月參考作物需水量(ET0)[24],如表2。水稻生育期各月的作物系數通過參考文獻[13]和[23]和實地調研獲取，計算公式如下：

ETC=KC×ET0

(22)

表2 1988—2018年5—8月參考作物需水量(ET0)情況Table 2 Reference crop water requirement (ET0) from May to August, 1988-2018 mm

式中：ETC為實際作物需水量計算值，mm；KC為作物系數；ET0為參考作物需水量，mm。

3 結果與分析

3.1 遙感GPM數據與降雨量的相關性

圖2顯示隨著采樣序列的變化，GPM值和雨量站降雨量變化趨勢相似，但是GPM值明顯高于雨量站站點降雨量，這表明GPM值存在一定的高估問題。通過趨勢圖可以明顯看出，GPM遙感數據與雨量站點降雨數據集有著明顯的趨勢一致性，所以可以采用線性回歸方法分析。

圖2 GPM值與雨量站降雨量變化情況Fig.2 Variation of GPM value and precipitation at precipitation station

3.2 空間降雨數據集

通過前面趨勢圖可以明顯看出，GPM遙感數據與雨量站點降雨數據集有著明顯的趨勢一致性，傳統水資源優化配置中使用的降雨量數據集都是基于以點帶面的形式，未考慮各個分灌區的空間變異性，為進一步提升降雨數據集的準確性，本研究采用一元線性回歸方法，通過2.1.1的方法計算，可以得到回歸方程如下：

Yj=0.046+0.714Xj

(23)

式中：Yj是第j個網格的ULR結果值；Xj表示第j個網格上GPM的月標準化值。

利用漳河灌區全流域多個雨量站點2014年5—8月各月的降雨數據，利用公式23，在ArcGIS中進行空間線性回歸，得到全流域的各月降雨的空間線性回歸結果。通過采用2.1.1的方法，首先將線性回歸結果與雨量站降雨數據進行對比，然后對殘差采用IDW方法進行插值，最后使用按掩膜提取工具，用漳河灌區各個分灌區邊界圖提取各個分灌區的降雨結果，得到2014年漳河灌區各個分灌區5—8月降雨的空間分布,見圖3。如圖所示隨著月份的變化，各個灌溉分區的降雨量具有明顯的變化，而且即使在同一月，各個分灌區的降雨量也有明顯的空間變異性。

由于降雨受地形、氣象等多種因素的影響，降雨量在估算過程中存在不確定性。區間參數能較好地描述空間插值過程對降雨量的不確定性。將降雨空間分布結果圖中各個分灌區降雨量的最大和最小值>乘以有效降雨系數，從而得到有效降雨量的上下界。圖3顯示四干渠的降雨量變異性最為顯著，降雨量最高最低值差異較大，說明該區域空間變異性較大，而且不同月份降雨量差異性也較大，時間變異性也較為明顯。而副壩、一干渠、西干渠降雨量差異性不明顯，說明這些灌溉分區的降雨情況相對穩定。

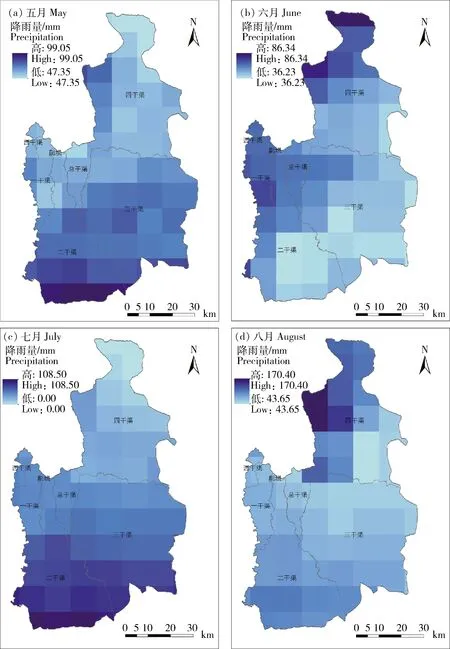
圖3 2014年漳河灌區各個分灌區 5—8月降雨的空間分布Fig.3 Spatial distribution of precipitation in each sub-irrigated area of Zhanghe irrigation area from May to August in 2014

隨后將交叉驗證方法[9]用于與GPM數據，線性回歸(ULR)，IDW方法和ULRR進行比較來衡量ULRR方法的適用性。其中，均方根誤差(RMSE)，平均絕對誤差(MAE)和平均相對誤差(MRE)是用于評估不同方法準確性的重要指標。可以計算每個方法的3個指標，RMSE、MAE和MRE，結果見表3。在這些方法中，ULRR方法的性能最好，表明ULRR方法可以提高預測結果的精度。

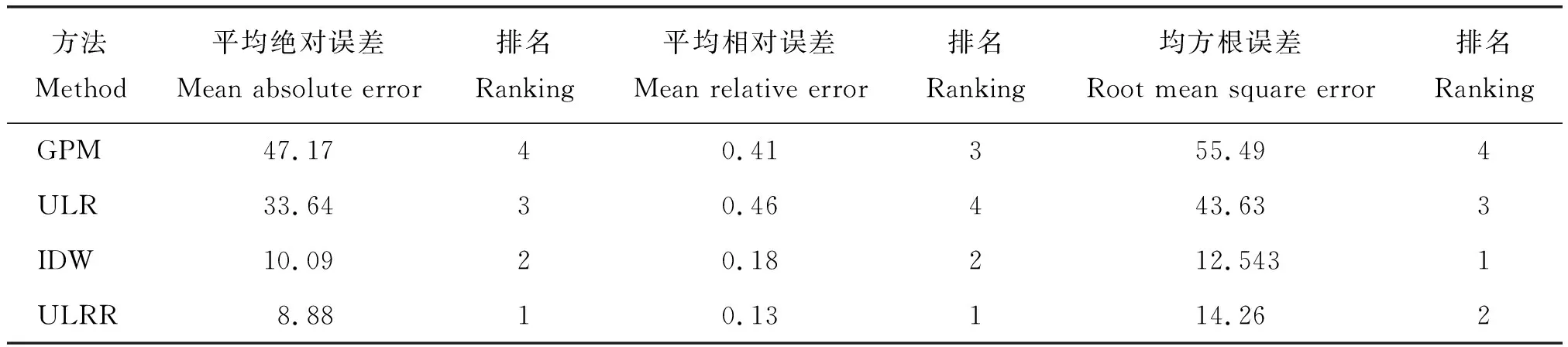
表3 GPM, ULR, IDW, ULRR方法的平均絕對誤差，平均相對誤差，均方根誤差測算結果Table 3 Test results of mean absolute error, mean relative error, root mean square error by using GPM, ULR, IDW and ULRR methods

3.3 不同可信度水平下最佳灌水量配置

表4為漳河灌區在可信度水平為0.8情況下不同分灌區5、6、7和8月的最優農業灌水量分配。可知：灌溉與降雨可以很好地滿足二干渠、四干渠、西干渠各個月的作物用水需求，5月相較于其他階段需水量滿足程度較低，這與5月的作物缺水敏感性較低的預期相一致。5月缺水程度最低的是二干渠和三干渠；6月二干渠和三干渠缺水程度顯著增高，這是由于降雨量隨著月份的變化，空間變異性較大的原因，分配到不同分灌區和不同月份的灌水量隨著降雨量的減少而增加。

表5為可信度水平為1時，各個分灌區5、6、7和8月中最佳農業灌水量分配。由于分灌區之間的不同月份降雨量變異性顯著，表5顯示各分灌區的最佳灌水量不相同，其中，副壩和四干渠的需水程度最大，一干渠、西干渠、總干渠次之。表5中顯示了作物主要生育期中5—8月的最佳分配水量，結果表明，當無法充分滿足5、6、7和8月需水量時，供水優先考慮6、7月，其次是8月，這個結果與作物的缺水敏感性、需水量和降雨有關，具體來說，總體5月的降雨可以滿足作物需水量，但隨著作物的生長，6、7和8月作物需水量顯著增加，而且這個時期的作物水分敏感性較大，而6月相對于7月作物需水量較低，容易被滿足，所以顯示6月滿足程度最高，而7月需水量滿足程度第二。根據表4和表5進行比對，隨著可信度水平的增加，對于6、7和8月的最佳灌水量無顯著影響，主要是提高了5月的配水量，這與前面5月缺水敏感性較低的預期一致。

表4和表5比較可以看出，隨著可信度水平的上升，8月最佳農業灌水量有一定程度的上升，這與8月敏感指數較大相一致；并且隨著可信度的上升，5月最佳農業灌水量也有一定程度上升，這可能是5月需水量滿足程度較低，所以可信度水平上升時，5月需水量滿足程度上升。隨著可信度水平的上升，系統的安全性和可靠性增強，系統的風險降低，這可以為灌區管理者提供參考[11]。

由表4和表5可知，盡管8月的四干渠和總干渠需水量最大，但分配水量較少，這與降雨量直接相關。降雨對灌水量分配影響較大，5月各個分灌區的最佳灌水量從南向西北依次遞增，6月最佳灌水量呈現從東南到西北依次遞減的趨勢。還可以看出，7和8月對缺水更加敏感。這兩個關鍵增長階段的缺水造成的生產損失很難通過其他增長階段的更多灌溉來彌補。因此，應優先考慮7和8月的灌水。因此，可提出以下幾點建議：1)考慮各個分灌區配水量的空間優先性，5月優先考慮副壩、總干渠、一干渠的配水，6月優先考慮二干渠和三干渠的配水，7月優先考慮四干渠、西干渠、副壩、一干渠的配水，8月優先考慮二干渠、三干渠、一干渠、副壩的配水；2)7月必須滿足作物需水量；3)模糊區間可信性約束非線性規劃模型得到的最優方案提供更好的選擇，保證灌溉供應不足時系統的效益。此外，最優農業灌水量分配結果有助于產生合理的灌水量分配，并減少枯水年降雨時空變異性大造成的缺水量。

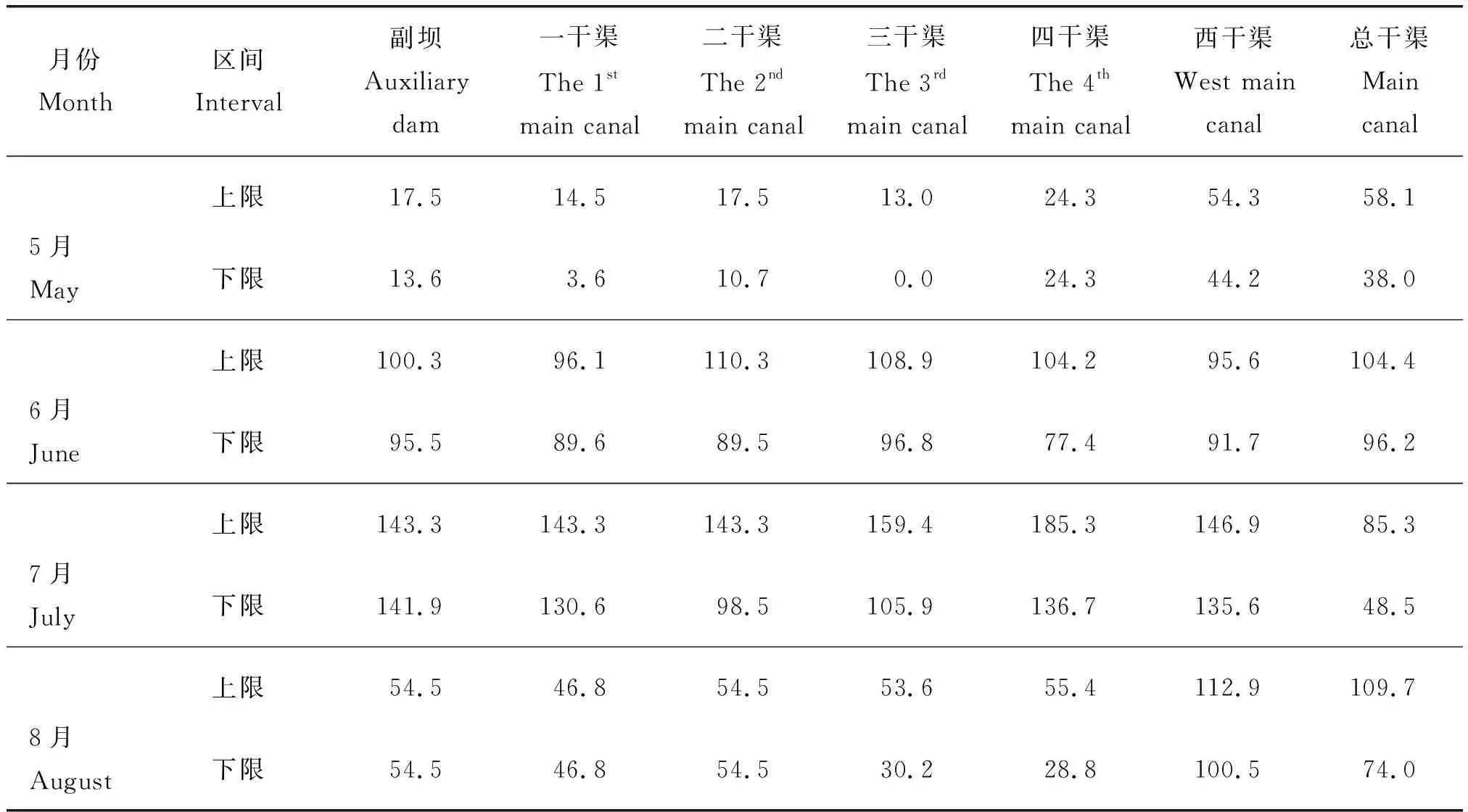
表4 可信度水平為0.8時的最佳灌水量上下限Table 4 Upper and lower limits of optimal irrigation amount under the reliability level 0.8 mm

表5 可信度水平為1時的最佳灌水量上下限Table 5 The upper and lower limits of optimal irrigation amount when the reliability level is 1 mm

3.4 凈系統效益

通過模糊區間可信性約束非線性規劃模型來分配各個分灌區的灌水量，從而獲得系統凈效益。在不同的可信度水平下，解決方案和相應的經濟效益也不同。由于輸入參數的不確定性，我們將解作為區間值給出，當可信度水平達到1時，系統效益達到[7.89×1010，2.61×1011]元，當可信度水平達到0.8 時，系統效益達到[7.88×1010，2.60×1011]元，可以發現隨著可信度降低，凈系統收益也有一定程度的降低。較高的可信度水平對應于模型結果的約束滿意度和較高的可信度水平，可信度水平可以被視為優化結果的可靠性的一個指標。灌水量是發展當地農業經濟的重要因素，實際上，應該更加注重降水量的時空變異性，從而對灌水量的在時間和空間上進行更好的統籌規劃；可信度水平越高，經濟效益越高，但對應的灌溉水資源總量也有所提升，灌區管理者應結合實際情況，選擇相應可信度水平下的方案，從而提高水資源利用率。

4 結 論

本研究構建了基于遙感數據的不確定性農業水資源優化配置模型，并將其應用于漳河灌區，得到了2種可信度水平下的最佳灌水方案。主要結論如下：1)ULRR方法預測結果的精度最高；2)漳河灌區各個分灌區的降雨量具有明顯的時空變異特征；3)在降雨情況和作物需水量情況相同的背景下，可信度水平越高，系統凈經濟效益越大；4)由于5月的缺水敏感性較低，而且缺水程度普遍較低，灌水量相對較少，在分配水量時，優先考慮7、8月的配水；5)此外，當可信度水平為1時，達到[7.89×1010，2.61×1011]元凈經濟效益，當可信度水平達到0.8時，系統效益達到[7.88×1010，2.60×1011]元。本研究驗證了模型在灌區尺度結合遙感數據進行單一糧食作物水資源優化配置的可行性，將為類似地區解決有限水資源配置問題提供配置思路與模型基礎。在實際的區域農業水資源配置中變異性較大的數據還有很多，因此在未來的研究中，可考慮基于本研究模型框架，構建結合多種空間參數的優化配水模型，來指導實際水資源配置。