基于RCMDE與概率神經網絡的滾動軸承故障診斷

陳 帥，黃晉英

（中北大學 機械工程學院，太原 030051）

0 引言

滾動軸承作為機械設備的重要部件之一，因其復雜的結構和惡劣的工作環境，在長時間運行后可能會出現各種各樣的故障，結果可能導致企業生產效率降低嚴重時甚至出現生命安全問題[1]。所以，對其故障診斷方法進行系統全面的探究具有十分重要的實際意義。如果發生了故障，相關的振動信號往往會具有非平穩以及非線性等方一系列特征。現有的非線性、非平穩性以熵值為特征參數的信號分析方法主要有：近似熵、排列熵、模糊熵、樣本熵等，但上述方法均為基于時間序列的單一尺度分析，分類效果較差[2]。之后又提出了多尺度熵算法，其優點是通過多尺度粗粒化過程使得熵擴展到多個時間尺度上，從多尺度表征故障信號的特征信息，進而解決了單一尺度熵的局限性，減小了偏差[3]。但是當數據序列較長時，會出現運算速度慢、故障信息丟失嚴重等問題，基于此，學者們提出一種精細復合多尺度散布熵（RCMDE）算法[4]，該方法能夠明顯改善在粗粒化過程中信息丟失問題。近年來，神經網絡已經獲得了廣泛的應用，它在非線性關系數據的處理領域中尤其顯著的優勢。概率神經網絡（PNN）的主要特點是有良好的并行處理、自學習以及自組織等方面的能力，可以在不同的精度水平之下向各種連續非線性函數進行逼近[5]。在此基礎上，本文以概率神經網絡（也就是PNN）以及精細復合多尺度散布熵（也就是RCMDE）為基礎首次提出了一種新的滾動軸承故障診斷分析方法，在研究的過程中，還和MDE-PNN法展開全面的分析與對比。所得到的結果表明，所提方法既能夠實現軸承故障的有效識別分類，且診斷效果優于MDE-PNN方法，平均分類精度達到了97.65%。

1 精細復合多尺度散布熵理論基礎

1.1 散布熵

散布熵是度量時間序列復雜性的非線性動力分析方法，對于長度為N的時間序列x=｛x1，x2，…，xN｝，其計算步驟如下[6]：

1）利用正態分布函數將時間序列x映射到y=｛yj，j=1，2，…，N｝，yi∈(0,1)，如式(1)所示。

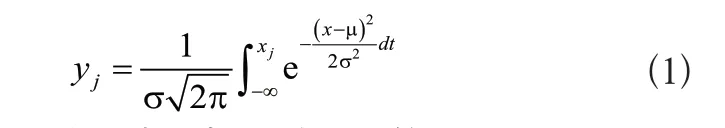
式(1)中，σ和μ分別表示標準差和均值。

2）線性變換將y映射到[1，2，…，c]，如式(2)所示。

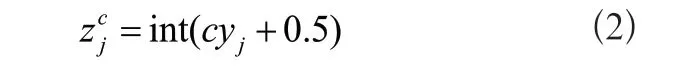
式(2)中，c是類別個數，int()是取整函數。

3）計算嵌入向量zm，ci：

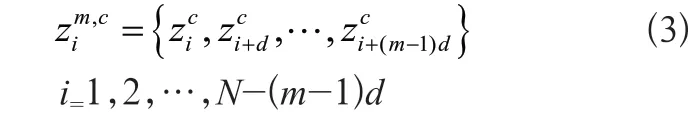
式(3)中，m是嵌入維數，d是時間延遲。

7)計算標準散布熵，公式如式(7)所示。

1.2 精細復合多尺度散布熵

RCMDE計算過程如下[7]：

1）多尺度粗粒化。給定原始數據u，其第k個粗粒化序列的計算如式(8)所示。

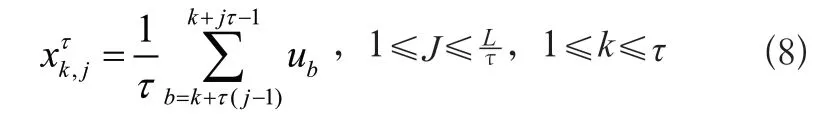
式(8)中，τ是尺度因子。

2）對每個尺度τ，RCMDE值定義如式(9)所示。

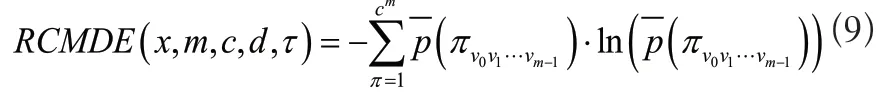
2 概率神經網絡

它為徑向基網絡當中的重要分支，主要的優點就是分類精度比較高，可以有效地利用簡單的線性模型訓練非線性模型，有效避免了BP神經網絡的局部最小值問題[8]。

PNN模型分為4層結構，第1層是輸入層，第2層是具有N個神經元的隱含層（N是訓練數據的數量），第i類樣本的第j個神經元的輸入與輸出關系由式(10)確定[9]。

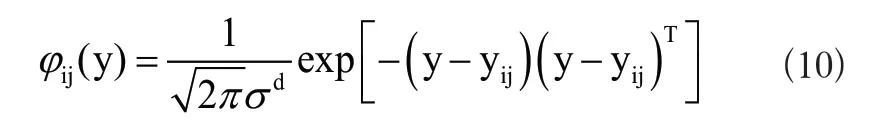
式(10)中是平滑因子，d為數據維度。

第3層是求和層，其把上一層中為同類的隱含層神經元的輸出按式(11)平均：

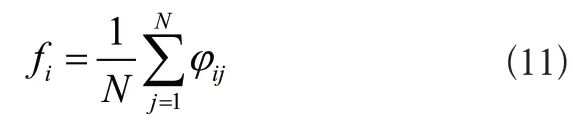
式(11)中，fi為第i類的概率。

第4層是神經元的輸出層，如式(12)所示。

式(12)中，z為輸出層的輸出。

3 實驗驗證

3.1 實驗設置

在本研究中將會通過西儲大學數據集來進行全面的分析與驗證。所采用的實驗臺詳見本文的圖1，其中有電子控制器、功率測試分析設備、扭矩傳感器以即電動機等多個重要的組成部分。軸承選用SKF6205-2RS，為了模擬軸承常見的4種狀態，采用電火花加工方式對軸承進行不同程度的單點損傷。選擇采樣頻率12kHz、電機轉速為1797r/min的驅動端軸承數據進行分析，每種狀態選擇80個樣本，共計320個樣本，每個樣本長度為4096，軸承狀態說明見表1。圖2為軸承時域波形圖。

圖1 實驗臺

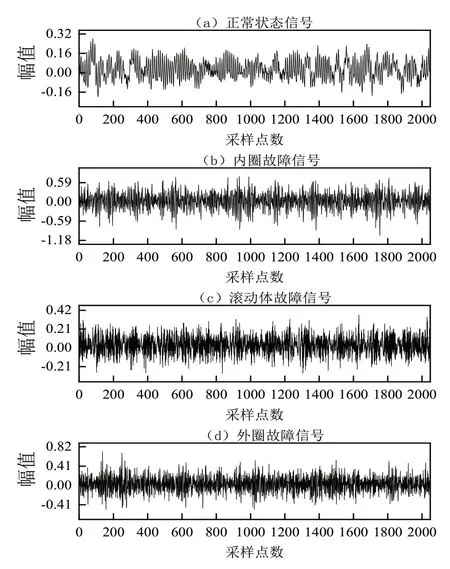
圖2 軸承4種狀態時域波形圖

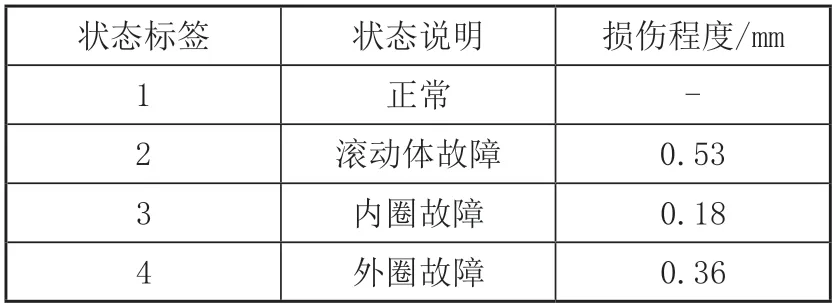
表1 軸承的4種狀態

3.2 實驗結果

計算320個樣本的RCMDE值，設置算法相關參數：最大尺度因子τ=20，嵌入維數m=2，延遲時間d=1。每種狀態不同樣本計算的熵值均值如圖3所示，可知，正常軸承振動信號RCMDE值遠大于3種故障狀態RCMDE值，并且變化趨勢明顯不同。對于排在前面的三個尺度，正常情況下，RCMDE值會隨著尺度逐漸提高而相依地提升，如果是出于故障的狀態中，那么它將會是始終下降的，尤其是由第三個尺度至第十個的過程中，將出現一定程度的波動現象，在此之后將比較的穩定。從整體上來看，RCMDE值與尺度因子成反比，在尺度因子達到11之后逐漸趨于平穩。

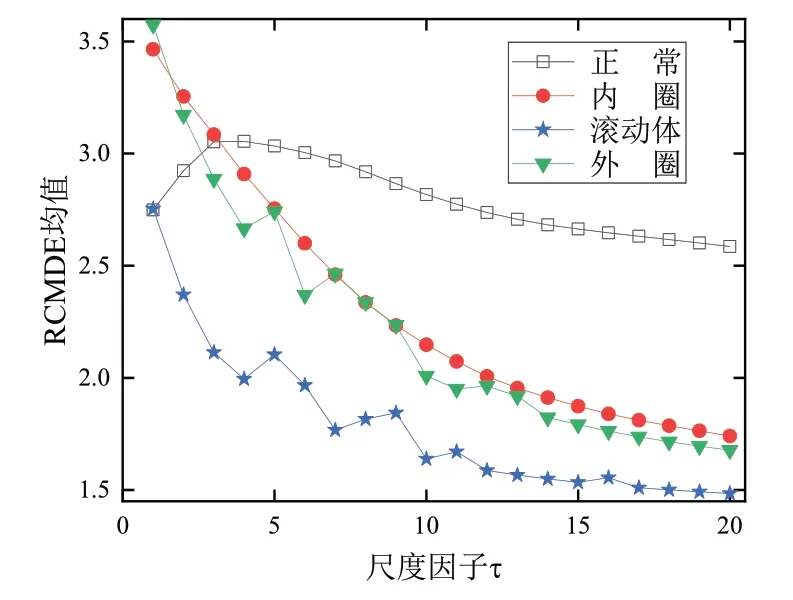
圖3 振動信號RCMDE均值

此外，還與MDE法展開全面的對比分析，以闡述RCMDE法所具有的主要優勢。計算每種狀態信號不同樣本MDE值，所得結果如圖4所示。對比圖3、圖4，可以看出：隨著尺度因子τ的增大，RCMDE值變化較MDE值變化相對平緩，從圖4可知，外圈和內圈故障從第5個尺度因子之后基本重合，不利于下一步分類器的識別分類，所以，選擇RCMDE值作為特征參數進行軸承4種狀態的特征提取較為合理。

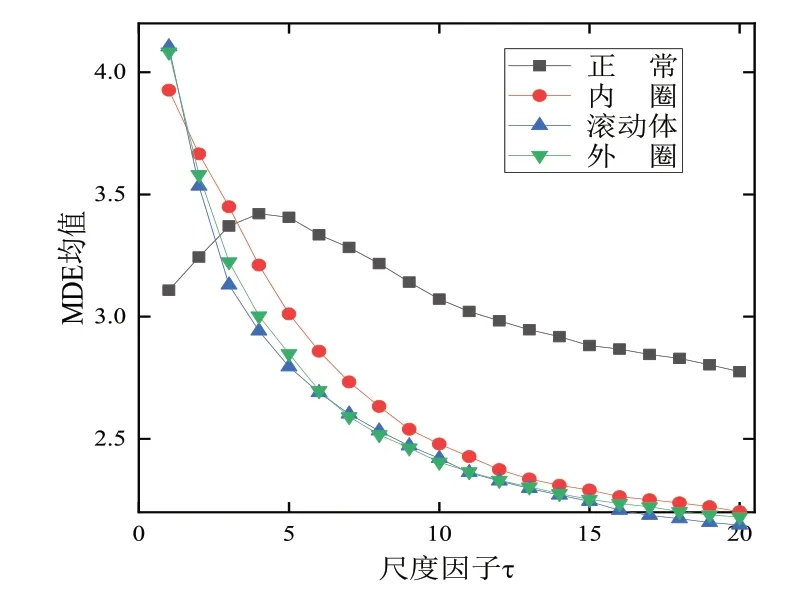
圖4 前20個尺度MDE均值

實驗隨機選取每種狀態的50個樣本作為訓練樣本，30個樣本作為測試樣本，為了減小實驗偶然性，對RCMDEPNN和MDE-PNN兩種模型分別進行10次實驗，結果如圖5所示。根據圖5可知，基于RCMDE-PNN的故障診斷方法分類效果明顯優于比MDE-PNN方法，分類準確率達到97.65%，而MDE-PNN的分類準確率為92.85%，分類準確率提高了4.8%。

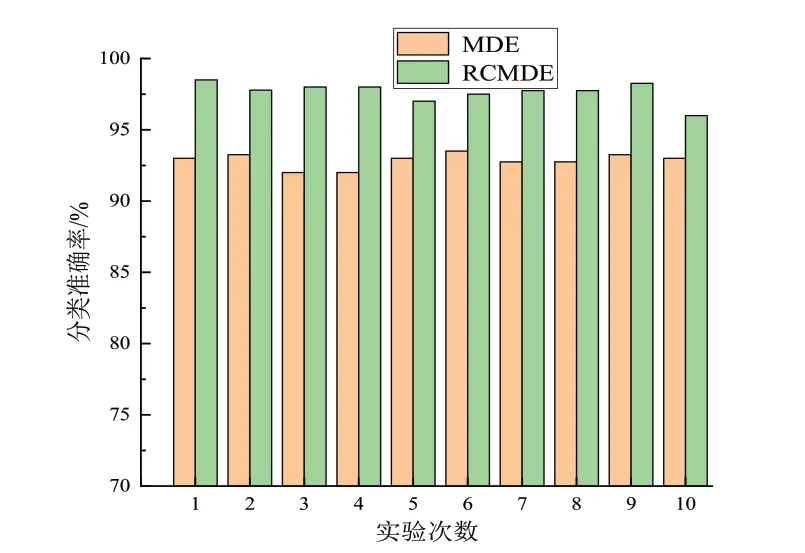
圖5 實驗結果

4 結語

1）引入一種檢驗振動信號復雜性的算法-精細復合多尺度散布熵（RCMDE），與MDE方法相比，RCMDE解決了單一尺度熵的局限性，實現了多尺度表征故障信號的特征信息，有利于下一步的故障識別分類；

2）RCMDE-PNN模型的軸承故障診斷準確率為97.65%，而MDE-PNN模型診斷準確率僅為92.85%，本文所提RCMDE-PNN方法，提升其分類準確率達4.8%，并且對它的優勢與有效性進行了全面的驗證。