一種ICS異常檢測的優化GAN模型

顧兆軍，劉婷婷，2，隋 翯

(1.中國民航大學 信息安全測評中心，天津 300300；2.中國民航大學 計算機科學與技術學院，天津 300300；3.中國民航大學 航空工程學院，天津 300300)

工業控制系統(Industrial Control System，ICS)是國家關鍵基礎設施的核心[1]，物理安全和網絡安全是其平穩運行的必要條件[2]。然而隨著工業控制系統逐漸接入互聯網，其網絡安全問題愈加凸顯[3-4]。工業控制系統網絡安全保障體系包括防護、檢測、響應和恢復4個層面[5]，檢測是其中重要環節，負責識別違反安全策略的行為或被攻擊的跡象[6-7]，為告警和響應提供必要信息。

檢測從技術角度可分為誤用檢測和異常檢測[8]。異常檢測由于對未知攻擊的高效識別，受到研究人員的廣泛關注，基于統計分析、基于數據挖掘、基于特征匹配和基于機器學習等方面的異常檢測研究成果頗為豐富。近年，基于深度神經網絡的異常檢測技術逐漸成為研究熱點[9-11]。自動編碼器網絡(AutoEncoder，AE)[12]、循環神經網絡(Rerrent Neural Network，RNN)[13]、長短時記憶網絡(Long-Short Term Memory，LSTM)[14]、卷積神經網絡(Convolutional Neural Networks，CNN)[15]和深度自動編碼高斯混合網絡(Deep Autoencoding Gaussian Mixture Model，DAGMM)[16]等深度神經網絡在應用中都取得了良好的效果。然而，工業控制系統的高實時性要求檢測方法準確率更高，誤報率更低；同時，工業控制系統中的類不平衡問題現象使分類器易于犧牲異常類來提高模型擬合能力，從而導致其準確率下降，泛化能力變差。

文獻[17]提出的生成式對抗網絡(Generative Adversarial Network，GAN)為工業控制系統異常檢測提供了全新視角。該模型通過生成器與鑒別器博弈，使生成器能夠不斷學習從隱空間到真實數據的映射，從而使生成數據更符合真實數據分布。但是傳統的生成式對抗網絡模型無法處理高維特征的圖像檢測問題，因此文獻[18]提出深度卷積生成式對抗網絡(AnoGAN)，設計了從圖像到隱空間映射的異常評分方法，實現了醫療圖像異常識別，并成功分割出了圖像中的異常區域。針對時間序列多元異常檢測問題，文獻[19]將GAN與LSTM-RNN相結合，提出了一種新的MAD-GAN模型。該模型同時考慮整個變量集特性以捕獲變量之間的隱空間交互，在異常評分中也同時考慮鑒別損失和重構損失，在多個數據集上的實驗結果表明該模型不僅具有優異的檢測性能，在維數縮減、迭代穩定性等方面也具有獨特優勢。文獻[20]的實驗研究也得到了類似的結論。然而，上述模型均為基于“單向”生成式對抗網絡模型的異常檢測方法，生成器需要學習真實數據對應的隱空間特征，即其先驗分布，從而導致檢測算法的時間復雜度很高，計算成本偏大。

為了提高隱空間特征的學習效果和學習效率，文獻[21]通過引入編碼器設計了雙向生成式對抗網絡(BiGAN)，使模型具備學習真實數據到隱空間逆映射功能，為數據添加了隱空間特征“標簽”，從而使模型具備了分類能力，尤其是在圖像分類和識別方面具有突出優勢。以雙向生成式對抗網絡模型為基礎，結合網絡入侵行為特征，文獻[22]率先提出高效異常檢測生成式對抗網絡方法(EGBAD)，并實驗證明了該方法不僅適用于圖像數據，在網絡入侵數據檢測中，尤其在時間復雜度方面具有優異性能。進一步針對入侵檢測中的離散數據，文獻[23]在BiGAN基礎上采用Dropout全連接網絡，并使用Wasserstein距離替代了交叉熵和JS散度，并提出一種由剩余損失加權求和計算鑒別損失的模型，使檢測準確率、召回率和F1得分都得到明顯提升。BiGAN模型雖然通過引入編碼器提高了真實數據得到對應的隱空間特征映射的學習能力，但處理數據類不平衡數據時，模型容易陷入局部最優。

因此，文獻[24]提出了一種采用“編碼-解碼-編碼”三層子網結構作為生成器的生成式對抗網絡模型——GANomaly。該模型通過使原始數據和二次編碼后數據的隱空間向量之間距離最小化，來學習正常數據分布；并通過被檢測數據與該分布之間的距離評斷是否異常，從而進一步提升了算法的學習能力。基于GANomaly思想，針對類不平衡數據，文獻[25]提出異常分數由表觀損失和潛在損失共同構成，并利用該方法通過對滾動軸承基準數據分析，實現了對物理機構的故障診斷。

上述已有研究成果充分說明基于生成式對抗網絡的異常檢測模型在處理類不平衡數據時具有獨特優勢。筆者提出了一種用于工業控制系統異常檢測的隱空間特征重構生成式對抗網絡模型——Latent Feature Reconstruction GAN(LFR-GAN)。在訓練階段，通過引入新的編碼器，學習生成數據到隱空間的映射，實現生成數據的隱空間特征重構，并嵌入SE Block(Sequeze and Excitation Block)模塊[26]提升有效特征權重，提高隱空間特征重構能力；鑒別器則同時鑒別兩個編碼器和一個生成器產生的3個數據對，加快模型收斂，提高模型精度和泛化能力。在檢測階段，綜合考慮重構和鑒別損失，借鑒WGAN-GP[27]研究思路，采用L2范數優化異常評分公式，克服模式崩塌[28]問題。最后，在公開數據集SWaT[29]和WADI[30]上對LFR-GAN模型進行了驗證，并與AnoGAN、BiGAN和WGAN-GP等方法進行了對比。結果表明，從學習能力、檢測能力、穩定性等方面，LFR-GAN模型都具有明顯的優勢。

1 LFR-GAN模型

模型分為訓練和檢測兩個階段。在訓練階段，模型通過編碼器E1、E2和生成器G與鑒別器D不斷對抗，學習正常樣本的數據分布和隱空間特征。模型訓練完成之后，基于訓練模型對未知狀態的測試樣本進行異常檢測。通過特殊設計的異常評分公式，計算待測數據樣本的異常得分并排序，根據經驗比例篩選出異常數據，從而判斷待測數據是否異常。模型算法流程如圖1所示。

圖1 LFR-GAN異常檢測模型算法流程

1.1 訓練階段

訓練階段如圖2所示，數據空間輸入樣本x經過編碼器E1編碼，得到其在隱空間的特征E1(x)；同時隱空間隨機噪聲z經過生成器G解碼，在數據空間得到生成樣本G(z)；然后生成樣本G(z)進一步經過編碼器E2編碼，得到生成數據在隱空間的重構特征E2(G(z))。從而，得到了3對由數據空間樣本和其隱空間特征組成的數據對——(x，E1(x))，(G(z)，z)和(G(z)，E2(G(z)))。鑒別器D通過鑒別這3個數據對得到鑒別損失，并根據鑒別損失逐步遞歸求解模型梯度，實現權重更新，反向優化編碼器E1、E2和生成器G。

訓練過程中，對于生成器，其使生成樣本G(z)盡可能接近真實樣本x；對于編碼器E2，其使重構的隱空間特征E2(G(z))盡可能接近于真實樣本對應的隱空間特征E1(x)；編碼器E1、E2以及生成器G通過與鑒別器D不斷對抗博弈實現迭代優化，以使鑒別器越來越難以分辨這3個數據對的來源，使得生成數據趨近于真實數據，隱空間的重構特征趨近于真實數據映射到隱空間的特征。

對于鑒別器，其目標是準確分辨出3個數據對的來源，并給出數據對來自于生成數據的可能性。當數據對來自真實數據(x，E1(x))時，鑒別器給出的數據對來自于生成數據可能性判據D(x，E1(x))應趨向于0，當數據對來自生成器(G(z)，z)或(G(z)，E2(G(z)))時，鑒別器給出的數據對來自于生成數據可能性判據D(G(z)，z)和D(G(z)，E2(G(z)))應趨向于1。

通過以上分析，該模型的訓練目標是實現一個最大最小二元博弈平衡：

(1)

而V(D，E1，E2，G)可表示為

V(D，E1，E2，G)=Ex～pX[Ez～pE1(·|x)‖D(x，z)‖w]+Ez～pZ[Ex～pG(·|z)‖1-D(x，z)‖w]+

(2)

圖2 LFR-GAN模型訓練過程示意圖

在訓練過程中，可以通過計算KID值[31](Kernel-Inception Distance)來評估模型學習訓練樣本分布的情況。KID值是真實樣本和生成樣本概率分布之間的差異，計算公式如下：

DKID=MMD(Pr，Pg) ，

(3)

其中，Pr為真實樣本的分布，Pg為生成樣本的分布，MMD(Pr，Pg)可表示為

(4)

(5)

其中，d為訓練集維數。

按式(3)～(5)可以計算隱空間特征z分布和真實數據編碼得到的隱空間特征E1(x)分布之間的KID值。KID值可以反映模型學習能力，KID值越小，表示兩個分布之間的差異越小，模型的學習能力越強。

1.2 檢測階段

模型訓練完成之后，將已訓練好的編碼器、生成器和鑒別器重組構成檢測模型，如圖3(a)所示。根據檢測模型產生的損失，使用異常評分公式來計算檢測數據的異常得分S：

S=λLG+(1-λ)LD，

(6)

其中，λ是一個常量，根據經驗取0.2；LG為重構損失，用來衡量測試樣本和生成樣本的差異；LD為鑒別損失，用來衡量(x，E1(x))和(G(E1(x))，E2(G(E1(x))))兩個數據對特征匹配損失，以評估生成數據是否和真實數據有相同的特征。

圖3 LFR-GAN模型檢測過程示意圖

LG和LD的計算公式如下：

LG=‖x-G(E1(x))‖2，

(7)

LD=‖fD(x，E1(x))-fD(G(E1(x))，E2(G(E1(x)))‖2。

(8)

式(7)中的x為測試數據，E1(x)表示該數據編碼后的隱空間特征，G(E1(x))表示將編碼器E1生成的隱空間特征解碼后的生成數據。式(8)中fD為嵌入鑒別器中的中間層，如圖3(b)所示，fD(·)為該中間層的輸出。L2范數對異常值更加敏感，更有利于得到穩定解，因此采用L2范數對LG和LD兩個損失函數進行計算。通過以上計算，測試數據的異常評分越高，越有可能為異常。在計算出所有樣本的異常分數后，將數據按異常分數降序排列，根據經驗預先設置異常比例，將異常分數處于該比例范圍內的樣本標記為異常。

2 實驗與結果

2.1 實驗設置

實驗采用SWaT和WADI兩個公開數據集，SWaT(the Secure Water Treatment)是一個水處理操作實驗系統，數據集采集了11天實驗數據，其中最后4天里共發動36次攻擊。WADI(WAter DIstribution)是一個分布式跨區域水務管道系統，連續16天采集了系統的網絡流量、傳感器和執行器數據，其中只有2天具有攻擊數據，二者均是典型的類不平衡數據集。本實驗將兩個數據集均分成訓練集和測試集。兩個訓練集中所有數據均為正常樣本。兩個測試集異常樣本占比分別約為11.98%和5.99%，數據集詳細信息如表1所示。

表1 SWaT和WADI數據集情況

實驗使用Intel 酷睿i7 9750H處理器和NVDIA GeForce GTX 1650顯卡，于Tensor Flow 1.14.0架構在Python 3.6下實現。實驗采用Adam優化器，學習率r=0.000 01，隱空間向量維度設為256，隱藏層維度設為128，訓練輪數根據經驗設置為60。

2.2 實驗結果和分析

首先，根據式(3)～(5)計算LFR-GAN模型在SWaT和WADI兩個數據集上的KID值隨迭代次數變化，來檢驗模型在訓練階段的學習能力，并與AnoGAN，WGAN-GP和BiGAN進行對比，結果如圖4所示。

由圖4可知，隨著迭代次數增加，LFR-GAN模型KID值基本處于0.1以下，明顯低于AnoGAN和WGAN-GP，與BiGAN相比也可以得到更低值，表明LFR-GAN模型得到的隱空間特征z分布和真實數據編碼得到的隱空間特征E1(x)分布間差異更小，模型的學習能力更強。在WADI數據集的初始學習階段，LFR-GAN模型KID值出現一些偏大值，是由于LFR-GAN模型在學習高維數據時尚未達到最優結果；隨著迭代次數增加，LFR-GAN模型KID值逐漸回落到低值穩定狀態，模型表現出明顯的學習能力優勢。

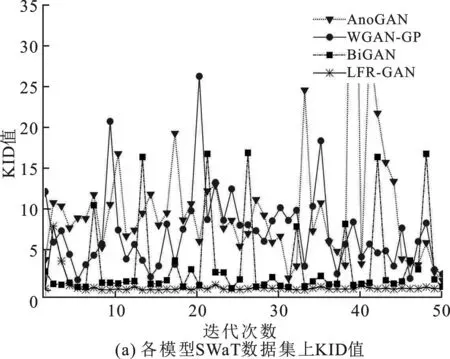
此外，隨迭代次數增加，除在WADI數據集的初始學習階段出現一些波動外，LFR-GAN模型KID值基本處于穩定狀態，而AnoGAN，WGAN-GP和BiGAN均出現較大幅度的波動且在實驗參數范圍內未見收斂趨勢。說明與上述3個模型相比，具有SE Block的LFR-GAN模型有更好的學習穩定性，可以在更少的迭代次數下達到最佳學習狀態。

工業控制系統異常檢測注重檢測效率，異常的出現往往會造成巨大的損失，所以在檢測階段更關注召回率，并兼顧準確率、精確率和F1得分。實驗使用召回率、精確率和準確率來反映模型的檢測性能，F1得分作為召回率和精確率的調和平均，檢測結果如圖5所示。

由圖5可知，LFR-GAN模型在SWaT數據集上的召回率為0.971 7，在WADI數據集上的召回率為0.996 3，相比其他模型，LFR-GAN模型的召回率大概可以提高2%～8%。召回率提高意味著異常數據誤報率降低，LFR-GAN既可以更準確地識別異常樣本，提高系統的安全性，又可以兼顧系統的實時性，避免由于誤報率過高導致的系統無效響應。實驗結果表明，基于隱空間特征重構的LFR-GAN針對不平衡數據集，相比其他模型具有更好的檢測性能。

此外，LFR-GAN模型的準確率和精確率均高于其他模型，在SWaT數據集上的準確率為0.933 7，精確率為0.952 3；在WADI數據集上的準確率為0.970 6，精確率為0.976 9。相比其他模型，準確率提高了約5%～11%，精確率提高了約2%～7%。精確率提高意味著漏報率降低，LFR-GAN可以更好地預測異常數據。上述表明LFR-GAN無需使用異常樣本進行訓練，也可實現高準確率和高精確率。并且LFR-GAN模型的F1得分也高于其他模型，在SWaT數據集上的F1得分為0.956 4；在WADI數據集上的F1得分為0.971 5，相比其他模型，F1得分大概提高了3%～8%。F1得分作為模型的綜合評價指標，它同時考慮精確率和召回率，讓兩者達到一個平衡點。所以F1分數在一定程度上反映了模型的綜合性能和穩定性，F1值越大，模型綜合性能和穩定性越好，進一步說明了LFR-GAN模型的優勢。

由于精確率-召回率曲線(Precision-Recall Curve，PR曲線)對樣本比例敏感，本實驗還使用PR曲線來衡量模型在類不平衡情況下的異常檢測性能，結果如圖6所示。

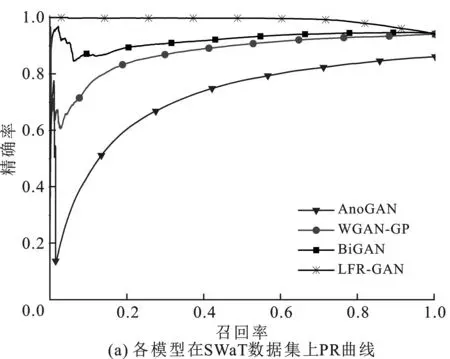
PR曲線可以用來對比分類器間的性能優劣。由圖6可知，LFR-GAN在兩個數據集上的PR曲線均可包圍其他三個模型的PR曲線，曲線與坐標軸圍成的面積最大。因此，LFR-GAN模型的分類性能最優，BiGAN較好，WGAN-GP中等，AnoGAN性能最差。可見，在類不平衡情況下，LFR-GAN模型的PR曲線更飽滿，對應的曲線下面積更大，分類性能更好，與圖5結果相一致。

實驗通過每次迭代得到的PRC AUC(Area Under Curve)值來反映模型在檢測階段的運行穩定情況。PRC AUC值即為PR曲線下面積，它能夠說明模型在驗證階段的性能，面積越大，表示分類器的性能越好。在模型每次迭代后進入檢測階段，得到PRC AUC值并與AnoGAN、WGAN-GP和BiGAN進行對比，結果如圖7所示。

由圖7可知，從第一次迭代開始，LFR-GAN的運行數值一直高于其他模型，并處于上升的階段。模型趨于穩定后，在WADI數據集上，LFR-GAN的PRC AUC值最優時接近1。上述結果說明，模型趨于穩定后，LFR-GAN模型運行的情況最好。此外，隨迭代次數增加，LFR-GAN模型基本在10次迭代內PRC AUC值達到最大，且運行平穩，而AnoGAN的值最低，WGAN-GP和BiGAN模型需迭代15～30次后才能達到穩定。實驗證明了子網結構采用卷積神經網絡的LFR-GAN能更好地提取樣本的局部特征，且具有隱空間特征重構的模型可用更少的迭代次數完成學習，達到最優狀態，模型具有更好的運行穩定性。

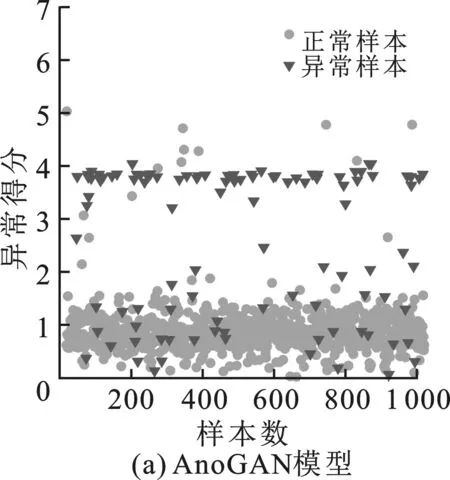
為了更直觀地展示各模型異常檢測的效果，實驗分別在SWaT和WADI測試集隨機選取1 000個樣本點，根據設定的異常評分公式(式(6))計算每個樣本的異常評分，檢驗模型的分類能力，并與AnoGAN、WGAN-GP和BiGAN進行對比，結果如圖8和圖9所示。

LFR-GAN相比其他模型能更好地區分異常樣本，而AnoGAN和WGAN-GP均存在漏報的現象，BiGAN相對漏報率低，但沒有一個清晰的分類邊界。可見與其他模型相比，LFR-GAN特殊設計的異常評分公式，能夠更有效劃分正負樣本的界限。

3 結束語

筆者針對工業控制系統異常檢測工作中類不平衡問題，根據生成式對抗網絡架構，新增生成數據向其隱空間映射的編碼器，引入SE Block模塊，采用L2范數優化異常評分公式，提出了LFR-GAN異常檢測模型，并在SWaT和WADI數據集上進行了性能驗證。

與AnoGAN，WGAN-GP和BiGAN的對比表明，LFR-GAN模型在處理類不平衡問題時，訓練過程全部使用正常樣本，但卻可以獲得更好的學習性能、檢測結果和模型穩定性。可見LFR-GAN模型魯棒性更強，穩定性更好，具有很好的現實可用性和有效性。隨著檢測技術和設備性能不斷提升，計算能力和存儲能力不斷增強，LFR-GAN模型在ICS異常檢測中將更具有前景。