一種融合優化選擇策略的差分粒子群算法

張德華，郝昕源，張妮娜，魏 倩，劉 英

(1.河南大學 計算機與信息工程學院，河南 開封 475004；2.武警綜保中心運維室，陜西 西安 711700)

在分布式多傳感器多目標數據融合系統中，傳感器系統偏差配準的目標是準確估計并校正傳感器的固有系統偏差，為其后續的信息融合以及數據處理提供技術保障，其偏差配準質量將直接影響多傳感器多目標數據信息融合系統的性能與可靠性。

傳統的系統偏差配準算法有：① 基于最小二乘配準算法，這種算法忽略了測量誤差，把誤差完全歸于系統誤差，且計算量也會隨著數據增多而劇增[1]；② 基于極大似然算法，該算法只解決了二維模型，采用地球投影，存在模型不準確的問題[2]。為了解決此問題，KARNIELY等[3]提出了用神經網絡算法進行系統偏差配準，由于采用梯度下降算法，存在收斂速度慢、易陷入局部最小值以及出現“鋸齒”現象等問題[4-6]。研究者不斷探索新的有效的網絡訓練方法，有研究者提出了用粒子群算法(Partide Swarm Optimization，PSO)與網絡相結合的算法，但粒子群算法本身又存在進化后期種群多樣性缺失的問題[7-8]。為了克服這個問題，有人提出將差分進化算法與粒子群算法(Differential Evolution Particle Swarm Optimization，PSO-DE)相結合[9-14]，但此方法在兩個種群全局最優適應度值相差較小時，會出現不必要的信息交流誤差。

針對上述問題，筆者提出了一種融合優化選擇策略的差分粒子群算法(Optimal Selection Particle Swarm Optimization-Differential Evolution-Weigthed Networks，OSPSO-DE-WN)。首先構建一個用于計算系統偏差的權值網絡(Weighted Network，WN)；然后對其網絡連接權值進行優化，得到最優網絡連接權值，再將其輸入到權值網絡，根據構造的適應度函數，計算出最優系統偏差；最后用其配準目標的傳感器量測。

1 權值網絡系統偏差估計模型

筆者所提OSPSO-DE-WN算法首先構建一個用于計算系統偏差的WN系統模型，然后用融合優化選擇策略的全局最優位置算法優化更新網絡連接權值估計，進而得到最優系統偏差估計值。權值網絡系統偏差估計模型結構如圖1所示。

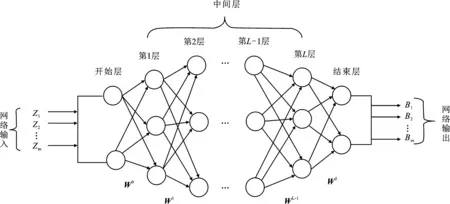
圖1 權值網絡模型圖

圖1中包含開始層、中間層和結束層的權值網絡，網絡連接權值將層與層連接起來。將網絡輸入值輸入到開始層，通過權值網絡的相關加權及非線性運算，將信息從開始層到中間層、然后再到結束層進行層層傳遞，在網絡結束層將網絡輸出值進行輸出。權值網絡的各層均由若干個端點組成，其中開始層和結束層的端點數由網絡輸入和網絡輸出的維數決定，中間層的端點數是根據經驗確定的。

假設有A類和B類傳感器量測點跡分別為Zi和Tz，表達式為

Zi=T+Bi+ni，i=1，2，…，M，

(1)

Tz=T+TB+Tn，

(2)

其中，T為目標參考真實點跡，Bi和TB為傳感器系統偏差，ni和Tn為隨機噪聲，Zi代表第i個A類傳感器的量測值，M代表傳感器的總個數，Tz代表B類傳感器的量測值。

A類傳感器精度較低，B類傳感器精度較高(TB和Tn值極小)，將B類傳感器量測作為目標參考真實狀態，A類傳感器量測數據作為待配準量測。WN系統偏差配準的實質就是將A的量測映射到B上。當隨機誤差遠小于系統偏差(即ni?Bi，Tn?TB)時，隨機誤差可以被忽略，也就是要求網絡實現Zi=T+Bi逼近Tz=T+TB；若將A類傳感器量測Zi作為網絡輸入，則系統偏差Bi也就是Zi-Tz為網絡輸出。網絡的輸入和輸出可由如下描述：

網絡輸入為Zi=(xi(k)，yi(k))，k=1，2，…，N，i=1，2，…，M。

(3)

網絡輸出為Bi=Zi-TZ=(xi(k)，yi(k))-(x(k)，y(k)) 。

(4)

而權值網絡模型結構的數學描述為

(5)

(6)

(7)

?

(8)

(9)

綜上所述，網絡最終輸出值可表示為

(10)

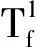
2 OSPSO-DE-WN算法框架

OSPSO-DE-WN算法主要包括兩部分：① 用帶有優化選擇策略的全局最優位置算法優化更新最優網絡連接權值估計；② 利用權值網絡計算系統偏差值，進而得到最優系統偏差估計值。具體的OSPSO-DE-WN算法框架如圖2所示。

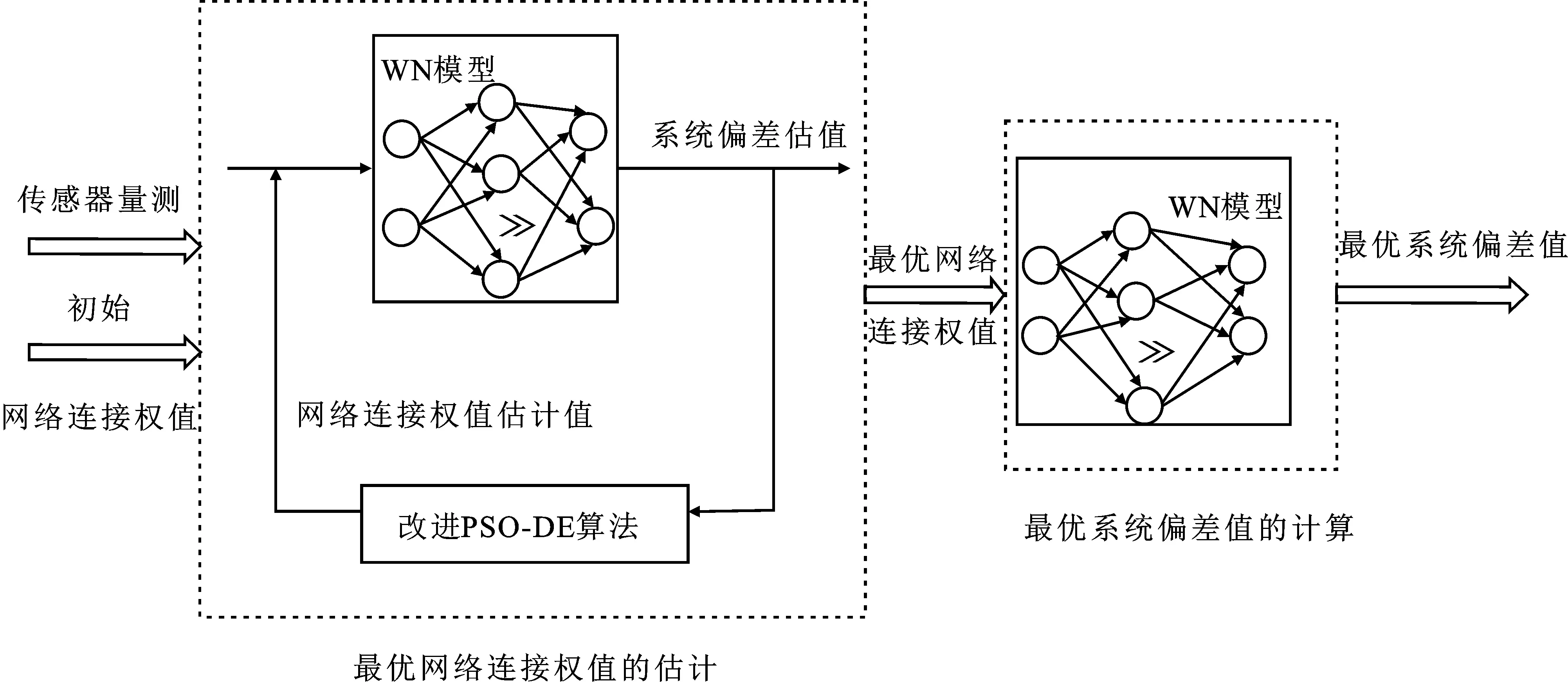
圖2 OSPSO-DE-WN算法框架

由圖2可知，首先取某時刻的傳感器對目標的量測值輸入到權值網絡，計算出對應的系統偏差值；然后，將系統偏差值輸入到文中所提算法中，通過遞推學習更新，得到此時刻最優的網絡連接權值；最后，將最優的網絡連接權值輸入到權值網絡，計算出此時刻最優的系統偏差估計值。

3 融合優化選擇的全局最優位置選擇

融合優化選擇策略的全局最優位置選擇如圖3所示。

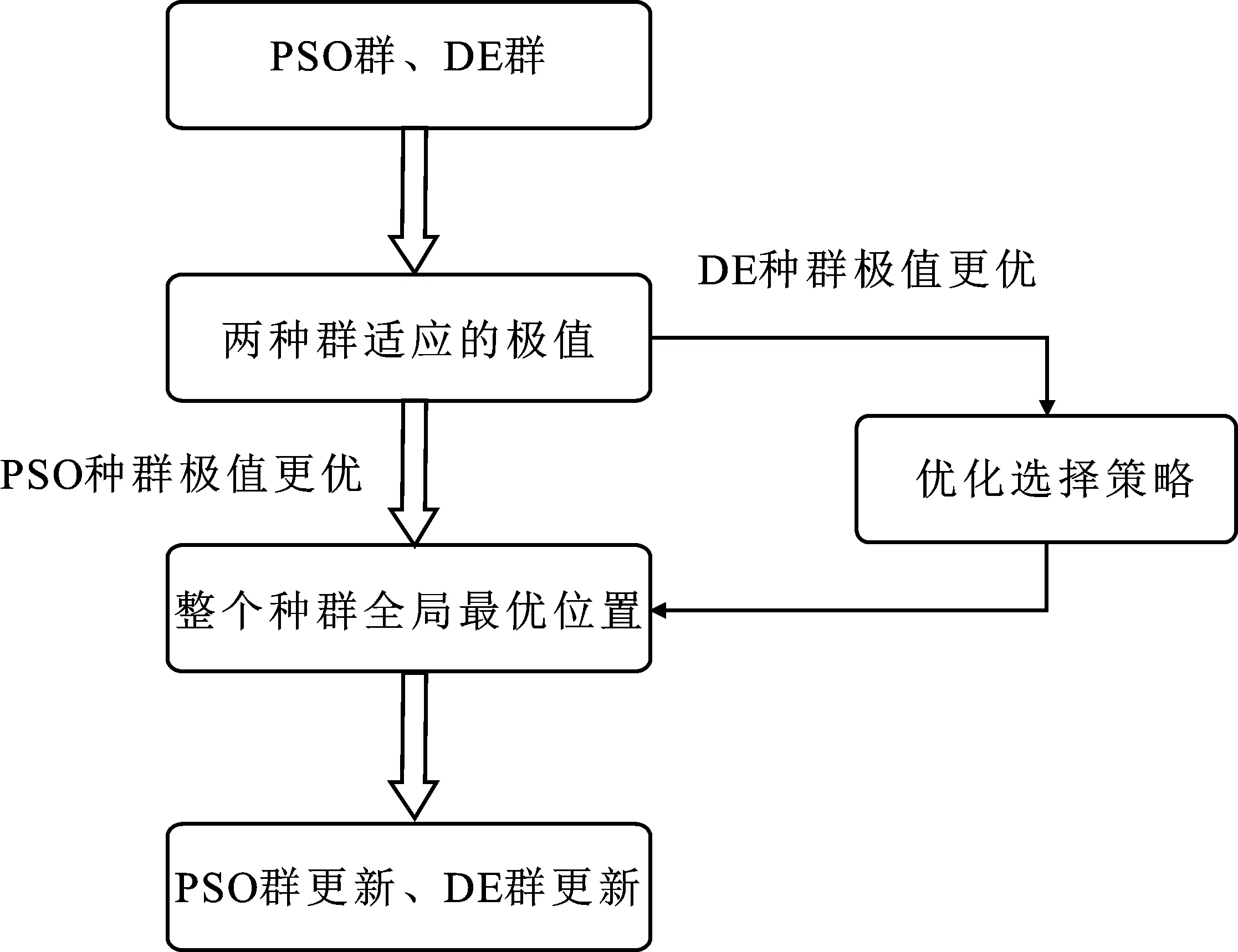
圖3 融合優化選擇策略的全局最優位置選擇

首先，計算每個種群中個體的適應度值并從中選出各種群中的最優個體，若PSO算法種群最優個體優于DE種群，則可直接確定整個種群的全局最優個體，即用PSO算法種群的最優個體作為整個種群的全局最優位置進行整個種群的更新；若DE種群最優個體優于PSO算法種群最優個體，則需要啟動優化選擇策略來確定整個種群的全局最優位置，即需計算2個最優個體適應度值的差值Df；然后判斷Df是否大于所設閾值df，若Df>df，則用DE種群最優個體作為整個種群全局最優位置，否則仍用PSO種群最優個體作為整個種群全局最優位置。這樣避免了在2個最優個體適應度值相差較小情況下，利用DE種群最優個體進行更新，不僅能加快收斂速度、節省算法運行時間，同時減小了信息交流誤差。

(11)

由式(11)知，Et越小，種群分布越不均勻；Et越大，分布越均勻，種群多樣性越好。故差值閾值函數df的公式可設定為

(12)

(13)

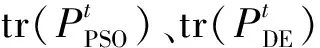
同時為了評價粒子優劣，筆者構造了一個適應度函數。適應度值越小，說明參考真實值與系統偏差估計越接近，估計出的系統偏差越準確。在系統偏差配準中，目標是得到最優系統偏差估計。為此可構造包含系統偏差估計和參考真實系統偏差在內的適應度函數：

(14)

4 仿真實驗與結果分析

為了說明筆者所提OSPSO-DE-WN算法在不同軌跡上的可行性及有效性，分別選取在二維平面內作非機動運動和機動運動的目標進行仿真驗證。

4.1 仿真場景及參數設置

目標的運動方程以及量測方程如下所示：

X(k+1)=FX(k)+μ(k) ，

(15)

Z(k)=HX(k)+B(k)+φ(k) ，

(16)

仿真場景1：假設目標在二維平面內作非機動運動，則非機動運動目標的狀態轉移矩陣表示為

(17)

量測矩陣表示為

(18)

其中，T為采樣間隔，設置為2 s。X方向上的速度設置為3 m/s，Y方向上的速度設置為4 m/s。目標狀態量X(k)的初始值X(0)設置為[100 m 3 m/s 200 m 4 m/s]T。X和Y方向上的傳感器系統偏差值分別設置為-3 m、5 m。

仿真場景2：假設目標在二維平面內作機動運動，則機動運動目標的狀態轉移矩陣表示為

(19)

量測矩陣表示為

(20)

場景2中，w表示轉彎因子。T為采樣間隔，取為0.1 s。X(k)的初始值X(0)設置為[200 m 8 m/s 100 m 2 m/s]T，X和Y方向的系統偏差值分別設為-6 m、8 m。在1～100 s，目標右轉彎運動，w取值為0.18 rad/s，在101～200 s，目標左轉彎運動，w取值為-0.2 rad/s。

表1給出了OSPSO-DE-WN算法中各仿真參數的符號及其具體設置值。

仿真實驗采用蒙特卡羅仿真形式，仿真次數設置為50次。采用的仿真環境為Intel i5，主頻為3.30 GHz，內存為4.00 GB，仿真軟件為Matlab R2014a。

表1 仿真參數設置

4.2 仿真結果及分析

為了證明筆者所提OSPSO-DE-WN算法的有效性和優越性，基于前述所設置的仿真場景和參數，并以系統偏差估計的均方根誤差值(RMSE值)作為算法精度的衡量指標，同時選擇PSO算法優化WN(PSO-WN算法)、PSO-DE算法優化WN(PSO-DE-WN算法)在非機動運動目標以及機動運動目標兩種場景下進行對比分析驗證。

首先，驗證種群多樣性以及個體適應度。以式(11)種群分布熵為衡量種群多樣性的指標，以式(14)適應度函數為衡量最優個體適應度指標。其仿真結果如圖4和圖5所示。

從圖4可以看出，隨著算法進化代數的增加，筆者所提OSPSO-DE-WN算法的熵值在進化代數為18的時候有一次微小的下降，之后幾乎穩定不變。這不僅說明OSPSO-DE-WN算法比PSO-DE-WN算法和PSO-WN算法的種群分布更均勻，也說明OSPSO-DE-WN 算法的熵值是最大的，其種群多樣性更加豐富。

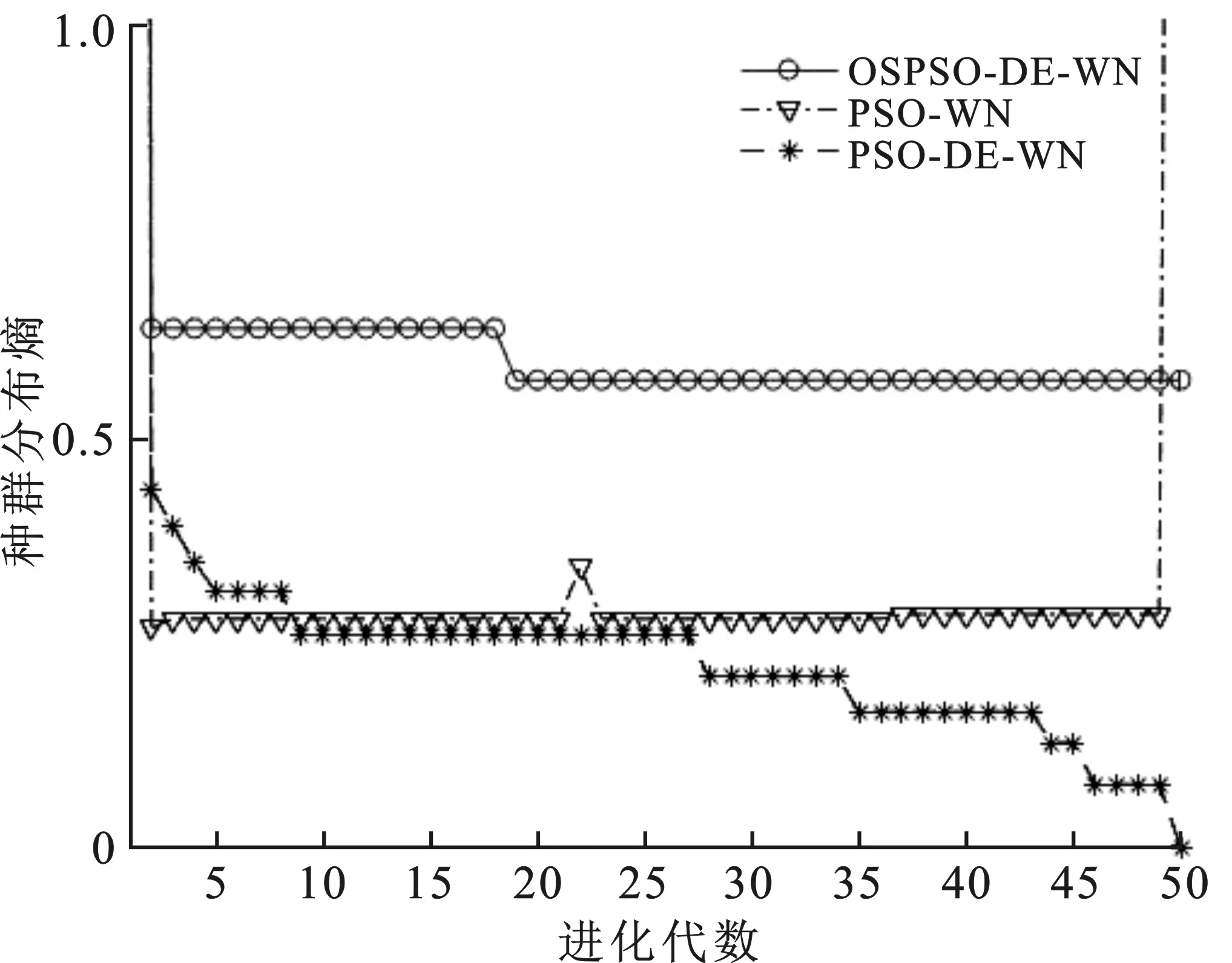
圖4 種群分布熵變化曲線

從圖5可以看出，OSPSO-DE-WN算法要比PSO-DE-WN算法和PSO-WN算法收斂速度快，而且經過50次的迭代進化，PSO-WN算法得到的最優個體適應度值為0.001 1；PSO-DE-WN算法得到的最優個體適應度值為4.763 1×10-4；OSPSO-DE-WN算法得到的最優個體適應度值為2.019 4×10-5。由式(14)適應度函數可知，適應度值越小，估計出的系統偏差值越接近于參考真實系統偏差值。這驗證了OSPSO-DE-WN算法搜索到的適應度值最小，最接近真實系統的偏差。

非機動目標情況下，將作非機動運動的目標的量測值輸入到OSPSO-DE-WN算法、PSO-DE-WN算法和PSO-WN算法中，估計出系統偏差值，如圖6～圖9所示。

圖6和圖7分別為目標非機動運動下3種算法在X方向和Y方向上的實際輸出系統偏差值與參考真實系統偏差值的曲線圖。3種算法在X和Y方向上估計出的系統偏差最終均趨于期望輸出系統偏差值-3 m和5 m。PSO-WN算法在1～45 s之間出現明顯波動，45 s之后基本穩定于參考真實系統偏差值附近。PSO-DE-WN算法在1～35 s之間出現明顯波動，35 s之后基本穩定于參考真實系統偏差值附近。從圖6和圖7均可以看出，OSPSO-DE-WN算法大約在2 s時收斂迅速，之后并逐漸收斂于真實系統偏差值附近。這充分說明OSPSO-DE-WN算法成功避免了兩種群在最小適應度值相差較小時，因信息交換出現的不必要信息交流誤差，同時也使得收斂速度更快，其運行時間也更短。

圖6 X方向上的系統偏差估計值

在蒙特卡羅仿真次數為50次，以及上述給定的仿真環境下，給出了3種算法的算法耗時，如圖8所示，同時也給出了3種算法收斂步長的比較，如圖9所示。

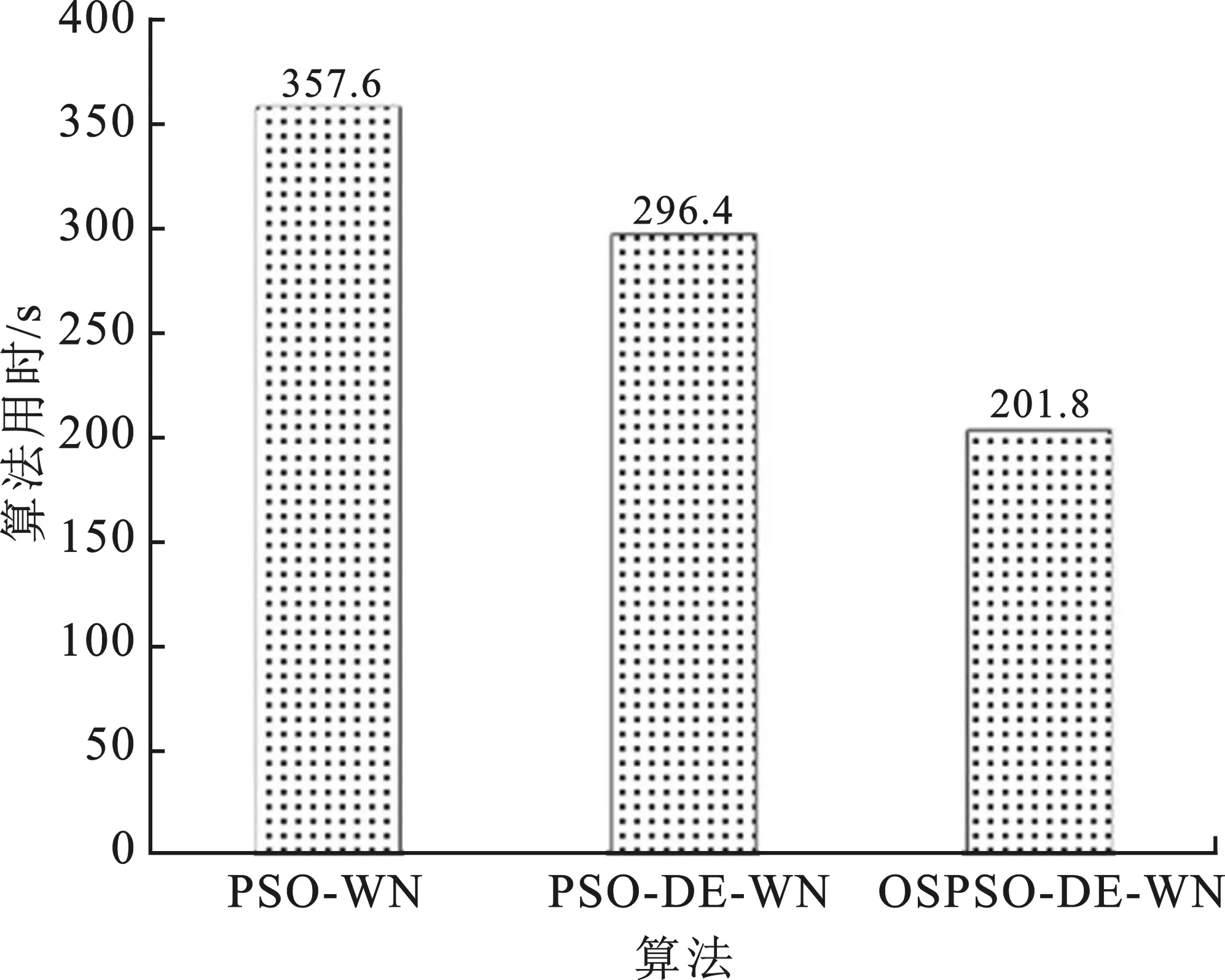
圖8 3種算法的耗時

從圖8可以看出OSPSO-DE-WN算法的運行時間要比PSO-WN算法、PSO-DE-WN算法的短；從圖9看出，OSPSO-DE-WN算法的收斂步長最小，進一步證明了筆者所提OSPSO-DE-WN算法的收斂速度要比PSO-WN算法和PSO-DE-WN算法的快。

根據前述結果得出傳感器系統偏差估計值，利用該估計值對傳感器的量測值進行系統偏差配準。非機動運動目標下3種算法配準前后的軌跡圖如圖10所示。系統偏差估計的平均均方根誤差如圖11所示。

圖10 非機動運動目標配準前后軌跡

從圖10和圖11中可以看出，筆者所提算法在具有前述優越性能的情況下，在非機動運動目標下配準后的軌跡比PSO-DE-WN算法和PSO-WN算法更加接近于參考真實軌跡。由圖11可以更直觀地看出，OSPSO-DE-WN算法在X和Y方向上系統偏差估計的平均RMSE值與PSO-WN算法以及PSO-DE-WN算法相比，數量級減少了一個數量級即101，這證明了在非機動運動目標場景下筆者所提OSPSO-DE-WN算法的精度要高于PSO-WN算法和PSO-DE-WN算法的。

機動目標情況下：將作機動運動目標的量測值輸入到OSPSO-DE-WN算法、PSO-DE-WN算法和PSO-WN算法中，仿真結果如圖12～圖17所示。

圖12 X方向上的系統偏差估計值

圖12和圖13分別表示機動運動目標下3種算法在X方向和Y方向上的實際輸出系統偏差值與參考真實系統偏差值的變化曲線圖。可以看出，3種算法在X和Y方向上估計出的系統偏差最終均趨于期望輸出系統偏差值-3 m和5 m。PSO-WN算法在1～25 s之間出現明顯波動，25～40 s之間輕微波動，40 s之后基本穩定于參考真實系統偏差值附近。但由于PSO-DE-WN算法融合了DE算法和PSO算法，使種群的多樣性增加，算法收斂速度變快。從圖12和圖13中也可以看出，在1～24 s之間出現波動，31 s之后基本穩定于參考真實系統偏差值附近。OSPSO-DE-WN算法大約在2 s時收斂迅速，之后穩定于參考真實系統偏差值附近。這充分說明OSPSO-DE-WN算法即使在機動運動目標情況下，也能有效避免兩種群在最小適應度值相差較小時，因信息交換出現的不必要信息交流誤差，同時運行時間也更短即收斂速度更快。

設定蒙特卡羅仿真次數為50次，在前述仿真環境下，從圖14給出了3種算法的算法耗時，同時圖15也給出了3種算法收斂步長。從圖14可以看出，OSPSO-DE-WN算法的運行時間為266.4 s，要比PSO-WN算法和PSO-DE-WN算法的短。從圖15看出，OSPSO-DE-WN算法的收斂步長要比PSO-WN算法和PSO-DE-WN算法小得多。這進一步驗證了OSPSO-DE-WN算法的收斂速度最快。

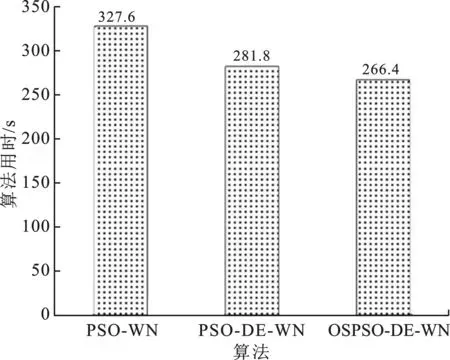
圖14 3種算法的耗時

根據文中前部分得出的傳感器系統偏差估計值，利用該值對傳感器的量測值進行系統偏差配準。目標機動運動下3種算法配準前后的軌跡如圖16所示。

從圖16中可以看出，筆者所提算法在具有前述優越性能的情況下，在機動運動目標下配準后的軌跡比PSO-WN算法、PSO-DE-WN算法更加接近于參考真實軌跡，使得系統偏差配準能夠更好地進行。從圖17可以更直觀地看出，OSPSO-DE-WN算法在X和Y方向上系統偏差估計的平均RMSE值與PSO-WN算法以及PSO-DE-WN算法相比，數量級減少了一個數量級即101，這充分說明在機動運動目標場景下，OSPSO-DE-WN算法的精度高于PSO-WN算法以及PSO-DE-WN算法的。

圖16 機動運動目標配準前后軌跡

5 總 結

針對系統偏差模型難以構建、粒子群算法出現種群多樣性變小和PSO-DE算法出現信息交流誤差的問題，筆者提出了一種帶有優化選擇策略的差分粒子群算法優化權值網絡的系統偏差配準——OSPSO-DE-WN算法。該算法首先構建了一個用于計算系統偏差的權值網絡，然后采用改進的優化策略對WN網絡連接權值進行優化更新，最后得到系統的最優偏差估計。實驗結果表明，該算法適應度值最小，無論在非機動運動目標還是機動運動目標運動場景下，都可有效提高種群多樣性并避免信息交流誤差，極大提高了收斂速度以及運算精度。