對(duì)數(shù)感與量感的辨析

吳立寶 高博豪 郭衎

摘要：數(shù)量感是指快速理解、估計(jì)和產(chǎn)生數(shù)量，并對(duì)數(shù)量進(jìn)行表征，以及理解數(shù)量間關(guān)系的能力。它去情境化分化為數(shù)感，強(qiáng)調(diào)抽象后的數(shù)值部分%卩情境化分化為量感，強(qiáng)調(diào)具體化的物理意義。數(shù)感與量感是一組對(duì)立統(tǒng)一的概念，由定性的思維形式在計(jì)算形式、求解策略、對(duì)象表征三個(gè)方面表現(xiàn)出一定的共性，又由各自的特征在外在表現(xiàn)、內(nèi)在價(jià)值、問(wèn)題表征、發(fā)展方向四個(gè)方面有所區(qū)別。關(guān)鍵詞：數(shù)量感;數(shù)感;量感

數(shù)量感是指快速理解、估計(jì)和產(chǎn)生數(shù)量，并對(duì)數(shù)量進(jìn)行表征，以及理解數(shù)量間關(guān)系的能力。"本能的數(shù)量感是感性且有局限的，例如，人類未經(jīng)學(xué)習(xí)無(wú)法借助數(shù)量感直觀感受較大的數(shù)量。學(xué)生的數(shù)量感經(jīng)過(guò)后天的培養(yǎng)可以趨于理性化，從而可以用數(shù)學(xué)的思維解決問(wèn)題。劉煒等通過(guò)測(cè)試發(fā)現(xiàn)，數(shù)量感可以是擺脫物理特征的抽象數(shù)量方面的感知，也可以是空間頻率、背景密度等方面的客觀實(shí)在維度的感知。?因此，數(shù)量感有向更為抽象的數(shù)及運(yùn)算（數(shù)感）分化的趨勢(shì)，也有向更為實(shí)用的物理量科學(xué)表達(dá)（量感）分化的趨勢(shì)。

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版'（以下簡(jiǎn)稱“2022年版課標(biāo)）在數(shù)感的基礎(chǔ)上新增量感的概念，并將數(shù)感與量感作為數(shù)學(xué)核心素養(yǎng)的兩個(gè)獨(dú)立的具體表現(xiàn)。數(shù)感是形成抽象能力的經(jīng)驗(yàn)基礎(chǔ)，主要是指對(duì)數(shù)與數(shù)量、數(shù)量關(guān)系及運(yùn)算結(jié)果的直觀感悟。量感是形成抽象能力和應(yīng)用意識(shí)的經(jīng)驗(yàn)基礎(chǔ)，主要是指對(duì)事物的可測(cè)量屬性及大小關(guān)系的直觀感知。?從數(shù)量感出發(fā)，逐步理清數(shù)感與量感的關(guān)系、共性與區(qū)別，有助于教師深人理解二者的含義，從而采取有針對(duì)性的教學(xué)策略，培養(yǎng)學(xué)生的數(shù)感與量感。

一、數(shù)感與量感的關(guān)系

劉煒等認(rèn)為，人類對(duì)數(shù)量表征的結(jié)果會(huì)產(chǎn)生一定的自主理解，這種感知能力最初來(lái)源于外界的真實(shí)刺激;同時(shí)研究發(fā)現(xiàn)，數(shù)量感不會(huì)因具體物體的個(gè)別屬性而受到干擾，例如改變兩個(gè)物體的大小與顏色，人類對(duì)其數(shù)量的感知結(jié)果仍然是兩個(gè)。！Wagner和Davis認(rèn)為，數(shù)量感是人類本能基礎(chǔ)上對(duì)物體數(shù)量的感知能力，包含數(shù)字和占位符兩部分，數(shù)字是從數(shù)量中去掉占位符之后的抽象結(jié)果，這里的占位符可以是數(shù)量單位、長(zhǎng)度單位等。"由此可以看出，數(shù)量感具有適度的抽象性和源于現(xiàn)實(shí)兩個(gè)主要特征。上述特征為數(shù)量感向數(shù)感與量感分化提供了基礎(chǔ)。

實(shí)際上，直到19世紀(jì)，皮亞諾算術(shù)公理體系確立，人們才真正區(qū)分開(kāi)數(shù)量與數(shù)。數(shù)量感向內(nèi)去情境化，分化為對(duì)數(shù)及其運(yùn)算結(jié)果以及相互關(guān)系的感知。例如，人類對(duì)數(shù)的認(rèn)識(shí)是在對(duì)數(shù)量認(rèn)識(shí)的基礎(chǔ)上忽略掉情境因素抽象而來(lái)的。學(xué)生借助數(shù)感進(jìn)行數(shù)的認(rèn)識(shí)及數(shù)的運(yùn)算時(shí)，依據(jù)的是抽象后的定義與法則，而非現(xiàn)實(shí)意義。數(shù)量感向外加情境化，則分化為對(duì)物理量及其基于度量單位的度量結(jié)果的感知。例如，人類將數(shù)量感與度量單位結(jié)合，遷移感知與表達(dá)各種物理量的大小。學(xué)生依據(jù)量感進(jìn)行目標(biāo)測(cè)量或估測(cè)的結(jié)果是數(shù)量在物理意義上的表現(xiàn)結(jié)果（如2米是同方向上2個(gè)1米的長(zhǎng)度和'此時(shí)需要依據(jù)現(xiàn)實(shí)意義，而非單純的運(yùn)算。上述兩個(gè)分化方向，即數(shù)感和量感兩大方向。

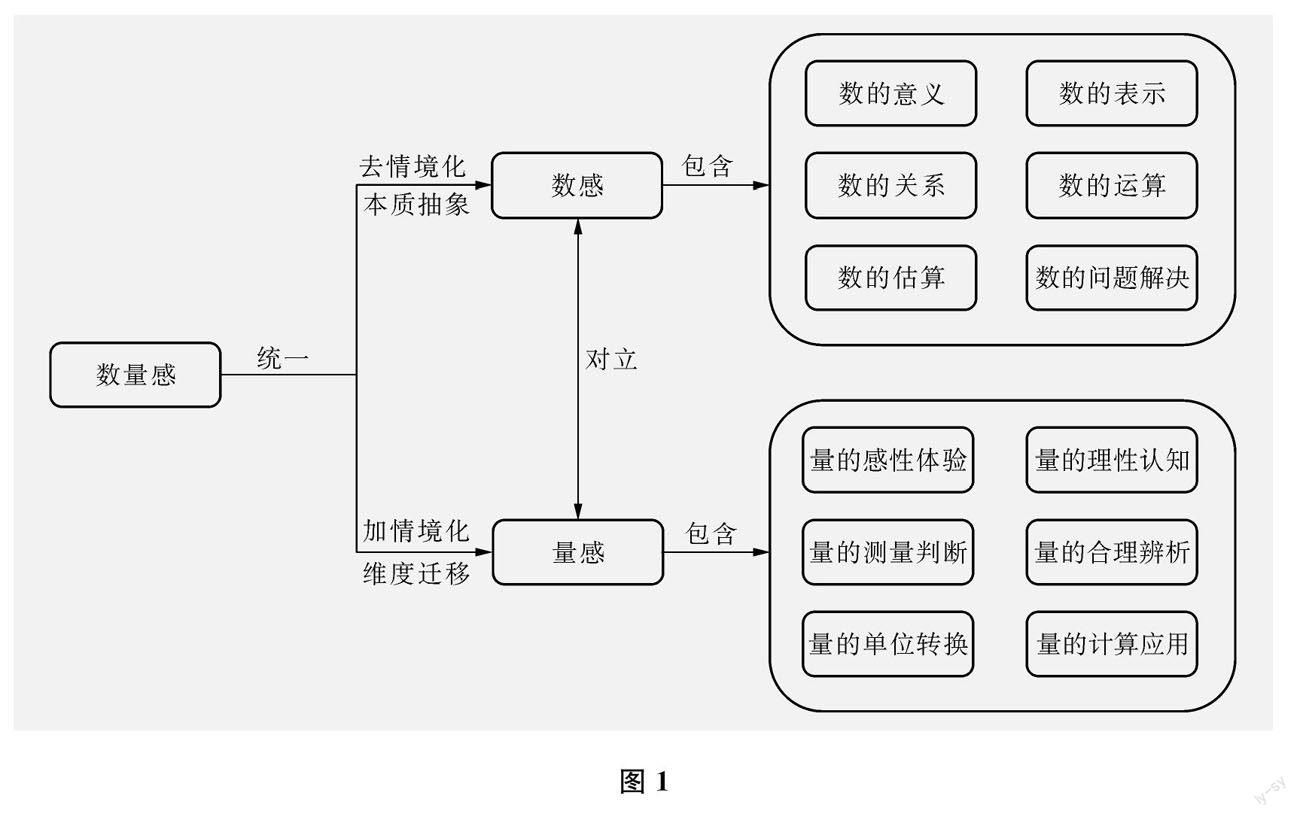
“數(shù)感”一詞最早出現(xiàn)在丹齊克的著作《數(shù)：科學(xué)的語(yǔ)言》中。丹齊克認(rèn)為，數(shù)感是對(duì)數(shù)集的感知能力，體現(xiàn)在對(duì)數(shù)集中數(shù)增減變化的明確感知。?對(duì)數(shù)感的解釋主要有以下兩種觀點(diǎn)：一種是行為取向的觀點(diǎn)，認(rèn)為數(shù)感是對(duì)數(shù)和運(yùn)算的一般理解，體現(xiàn)在計(jì)算求解問(wèn)題上$另一種是認(rèn)知取向的觀點(diǎn)，認(rèn)為數(shù)感是基于內(nèi)心的近似表征系統(tǒng)（ANS）產(chǎn)生的認(rèn)知結(jié)果的外顯'，這種能力是借助語(yǔ)言表達(dá)近似結(jié)果的（。在義務(wù)教育階段，數(shù)感包括數(shù)的意義、數(shù)的表示、數(shù)的關(guān)系、數(shù)的運(yùn)算、數(shù)的估算、數(shù)的問(wèn)題解決六部分。?量感是指對(duì)客觀事物大小的認(rèn)識(shí)：在感知度量單位的基礎(chǔ)上，通過(guò)一定的測(cè)量工具進(jìn)行測(cè)量或估測(cè)，借助大腦估算與心算，最終可以感性或理性地表達(dá)物理量的大小。量感強(qiáng)調(diào)對(duì)客觀物理量及其變化結(jié)果的感知，包括量的感性體驗(yàn)、量的理性認(rèn)知、量的測(cè)量判斷、量的合理辨析、量的單位轉(zhuǎn)換、量的計(jì)算應(yīng)用六部分。

總之，數(shù)感與量感均來(lái)源于數(shù)量感，它們的關(guān)系可用下頁(yè)圖1來(lái)表示。

二、數(shù)感與量感的共性

總體來(lái)看，數(shù)感與量感在思維形式上具有高度的相似性。曹才翰、章建躍認(rèn)為，計(jì)算包括精確計(jì)算、心算、估算三部分。精確計(jì)算主要指筆算，筆算的步驟是理性且嚴(yán)謹(jǐn)?shù)模涸诶斫馑憷淼幕A(chǔ)上，借助算法一步步從問(wèn)題出發(fā)，最終求得標(biāo)準(zhǔn)的計(jì)算結(jié)果。與精確計(jì)算不同，心算與估算則更多依賴于經(jīng)驗(yàn)，是直覺(jué)作用下的感性認(rèn)知，表現(xiàn)為計(jì)算規(guī)則內(nèi)化后，熟能生巧地得到較為準(zhǔn)確的運(yùn)算結(jié)果。因此，借助于心算、估算的思維模式屬于直覺(jué)判斷，是定性（而非定量）的思維形式。！這種定性的思維形式是數(shù)感與量感共性的起源，具體表現(xiàn)為計(jì)算形式、求解策略、對(duì)象表征二個(gè)方面的共性。

（一）計(jì)算形式方面的共性

在運(yùn)算過(guò)程中，數(shù)感多表現(xiàn)為對(duì)數(shù)及其關(guān)系的理解，通過(guò)估算而非復(fù)雜計(jì)算，快速且近似地求解，并結(jié)合自身的經(jīng)驗(yàn)，對(duì)估算結(jié)果給出合理的解釋。"其中，數(shù)量關(guān)系估算法是小學(xué)常用的一種估算方法。#例如，不計(jì)算比較下列式子的大小，在（? ）中填寫(xiě)“<”“>”或“=”：33+2（? ）33+3。觀察發(fā)現(xiàn)，左右兩邊的式子都有數(shù)字33，因此，左右兩式最終的大小取決于33加上的那個(gè)數(shù)的大小。因?yàn)?<3，所以33+2<33+3。上述判斷是基于數(shù)感的估算，而非計(jì)算得到35<36，從而得到比較結(jié)果。

在計(jì)算形式方面，量感與數(shù)感高度相同。比如，根據(jù)量感判斷目標(biāo)物體的重量時(shí)，往往將問(wèn)題轉(zhuǎn)化為借助日常經(jīng)驗(yàn)與所學(xué)知識(shí)進(jìn)行估算，從而得到合理的估測(cè)結(jié)果。一個(gè)例子是：借助日常生活經(jīng)驗(yàn)，知道1袋雞蛋大約有8個(gè)，整體重量大約是，5千克（1斤），進(jìn)而形成0.5千克的感知印象;之后，遇到與1袋雞蛋重量相近的物體時(shí)，不通過(guò)稱重或計(jì)算，便能快速估計(jì)出目標(biāo)物體的重量大約是0.5千克。再如，依據(jù)量感進(jìn)行單位轉(zhuǎn)換時(shí)，往往借助經(jīng)驗(yàn)的直覺(jué)進(jìn)行心算。以“1千克=1000克”的轉(zhuǎn)換為例，表現(xiàn)為“大”單位轉(zhuǎn)換為“小”單位，進(jìn)律是1000，那么直接在數(shù)字1后面添三個(gè)0即可;反之，則表現(xiàn)為將小數(shù)點(diǎn)向左移動(dòng)三位，而不是采用具體乘或除以1000的精確計(jì)算數(shù)值來(lái)感知換算結(jié)果。

（二）? 求解策略方面的共性

利用數(shù)感解決問(wèn)題，往往傾向于采用“嘗試一歸納一應(yīng)用”的策略。該策略的特點(diǎn)是高實(shí)效性，即可以借助直覺(jué)快速求解。具體表現(xiàn)為解決問(wèn)題時(shí)，嘗試用簡(jiǎn)便的方法簡(jiǎn)化處理，在驗(yàn)證結(jié)果準(zhǔn)確性的基礎(chǔ)上歸納，并把歸納后的結(jié)果作為認(rèn)知的支撐點(diǎn)，在練習(xí)的過(guò)程中強(qiáng)化，從而逐步減少思考的成本，使之變?yōu)橐环N直覺(jué)，并在未來(lái)解決問(wèn)題時(shí)應(yīng)用。例如，計(jì)算0.25X4時(shí)，借助嚴(yán)謹(jǐn)?shù)墓P算得到其結(jié)果為1。數(shù)字1起到了提醒的作用，因此，在遇到含有0.25X4部分的計(jì)算時(shí)，會(huì)嘗試跳過(guò)筆算，直接將得數(shù)1作為直覺(jué)結(jié)果進(jìn)行表征。同類的問(wèn)題還有1.25X8=10等小數(shù)乘法結(jié)果為整數(shù)的特征化計(jì)算。

在求解策略方面，量感與數(shù)感具有共同之處。比如，借助量感的經(jīng)驗(yàn)性，可以嘗試將目標(biāo)物體的長(zhǎng)度與自己身體的部位對(duì)比。例如，對(duì)比發(fā)現(xiàn)，書(shū)桌的長(zhǎng)度有一個(gè)半自己的胳膊那么長(zhǎng)，自己的胳膊長(zhǎng)大約是0.5米，因此，書(shū)桌的長(zhǎng)度在0.75米左右。在這一嘗試的基礎(chǔ)上，可以通過(guò)測(cè)量判斷結(jié)果的正確性一一借助尺子測(cè)得書(shū)桌的長(zhǎng)度為0.8米，與自身感知的結(jié)果相近。從而便可以此歸納，將目標(biāo)物體的長(zhǎng)度與自己的胳膊相關(guān)聯(lián)，借助胳膊的長(zhǎng)度快速求得結(jié)果，省卻嚴(yán)格的參照測(cè)量求解的步驟。

（三）? 對(duì)象表征方面的共性

就數(shù)感來(lái)看，其對(duì)象表征往往不是一個(gè)精確的數(shù)值，而是在誤差范圍內(nèi)可以接受的近似值，表現(xiàn)為投人的思考程度與輸出的結(jié)果精確度的權(quán)衡。借助數(shù)感解決問(wèn)題具有一定的實(shí)效性，因此，可以省卻大量的思考成本，得到一個(gè)在誤差范圍內(nèi)可以接受的結(jié)果。這種基于數(shù)感的結(jié)果往往對(duì)計(jì)算起到導(dǎo)向及驗(yàn)證的作用。例如，計(jì)算24X0.55時(shí)，會(huì)在頭腦中將問(wèn)題近似表征為24的一半是12，從而對(duì)最終的計(jì)算結(jié)果作出感性的判斷：若結(jié)果與12的偏差過(guò)大，則是錯(cuò)誤的。

近似性也是量感的一大特征，其核心在于，通過(guò)過(guò)程近似和結(jié)果近似的方式，簡(jiǎn)化解決問(wèn)題的過(guò)程，使結(jié)果在合理的誤差范圍內(nèi)快速呈現(xiàn)。過(guò)程近似，如將水瓶忽略瓶嘴部分近似為標(biāo)準(zhǔn)圓柱進(jìn)行體積估測(cè)，將球近似為其外接正方體進(jìn)行體積估測(cè)。結(jié)果近似闡述為將精確且復(fù)雜的測(cè)量結(jié)果通過(guò)合理簡(jiǎn)化，以簡(jiǎn)單明了的方式進(jìn)行表征，降低后續(xù)測(cè)算的難度。如將4.02厘米用4厘米簡(jiǎn)化處理，有利于快速感知數(shù)量結(jié)果。

三、數(shù)感與量感的區(qū)別

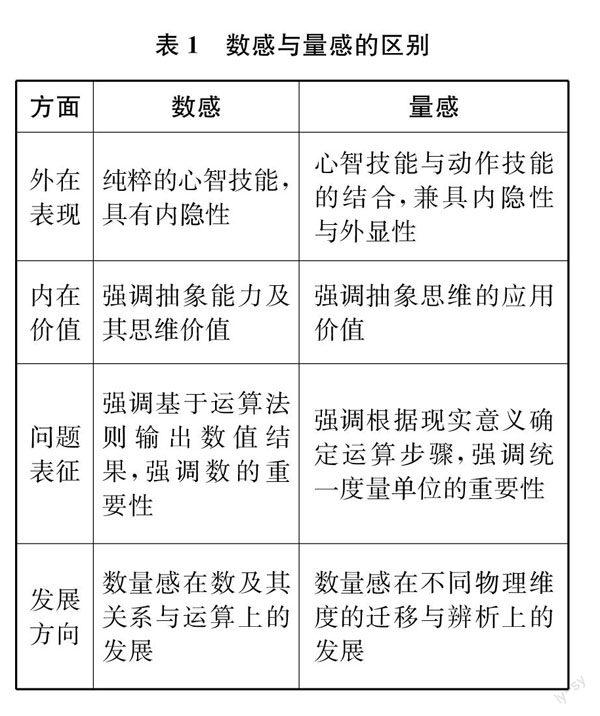
數(shù)感和量感又在各自特征方面呈現(xiàn)出很多的不同。具體來(lái)說(shuō)，可從外在表現(xiàn)、內(nèi)在價(jià)值、問(wèn)題表征與發(fā)展方向四個(gè)方面概括它們的區(qū)別，如表1所示。

（一）? 外在表現(xiàn)方面的區(qū)別

外在表現(xiàn)方面，數(shù)感與量感的主要區(qū)別在于：數(shù)感是純粹的內(nèi)在認(rèn)識(shí)活動(dòng)，沒(méi)有外在的動(dòng)作成分，即數(shù)量感的思維部分，因此具有內(nèi)隱性;量感是內(nèi)在認(rèn)知活動(dòng)與外在動(dòng)作活動(dòng)的結(jié)合，如估測(cè)與實(shí)測(cè)相結(jié)合，即數(shù)量感的操作驗(yàn)證部分，因此兼具內(nèi)隱性與外顯性。

數(shù)感表現(xiàn)為借助內(nèi)心的近似表征系統(tǒng)，通過(guò)對(duì)數(shù)字的理解以及心算與估算，得到表征后的結(jié)果。陳炳建認(rèn)為，用數(shù)思考是數(shù)感的基本表現(xiàn)形式。！若把數(shù)感視為一種技能，應(yīng)是純粹的心智技能，體現(xiàn)在通過(guò)人腦進(jìn)行認(rèn)知、估算與反饋，并以觀念上的結(jié)果作為認(rèn)知的結(jié)果。此時(shí)，個(gè)體可能并沒(méi)有實(shí)質(zhì)的動(dòng)作，但是在頭腦中已經(jīng)進(jìn)行了多次估算并整理了結(jié)果。因此，數(shù)感具有觀念性、內(nèi)隱性、簡(jiǎn)縮性等特征。例如，學(xué)生坐在座位上不動(dòng)，是已經(jīng)在頭腦中完成了11X12=11X10+11X2=110+22=132的一系列簡(jiǎn)算。

量感的表現(xiàn)有以下兩個(gè)模式：其一，通過(guò)量的理性認(rèn)知，在原有知識(shí)與經(jīng)驗(yàn)的基礎(chǔ)上，使用度量單位，通過(guò)“數(shù)+單位”的形式形成結(jié)果的表象，此時(shí)量感也表現(xiàn)出與數(shù)感類似的內(nèi)隱性;其二，2022年版課標(biāo)明確提出培養(yǎng)學(xué)生選擇合理的測(cè)量工具進(jìn)行測(cè)量的能力，測(cè)量屬于動(dòng)作技能，比如選擇尺子測(cè)量目標(biāo)物體的長(zhǎng)度，測(cè)量過(guò)程可以拆分為選擇尺子、對(duì)齊零刻度、目標(biāo)讀數(shù)等環(huán)節(jié)展開(kāi)動(dòng)作，這種動(dòng)作技能具有明顯的對(duì)象客觀性、執(zhí)行外顯性、結(jié)構(gòu)展開(kāi)性等特點(diǎn)。因此，量感的表現(xiàn)往往是感知與操作并舉，動(dòng)腦與動(dòng)手并行。

（二）? 內(nèi)在價(jià)值方面的區(qū)別

在內(nèi)在價(jià)值上，數(shù)感與量感的區(qū)別主要在于：數(shù)感側(cè)重于抽象能力及其思維價(jià)值，強(qiáng)調(diào)借助數(shù)量關(guān)系體會(huì)數(shù)的抽象過(guò)程以及運(yùn)算法則，即數(shù)量感中數(shù)的部分;量感強(qiáng)調(diào)抽象思維的應(yīng)用價(jià)值，即解決有關(guān)數(shù)量關(guān)系的實(shí)際問(wèn)題。

數(shù)感致力于逐步揭示數(shù)量感背后蘊(yùn)含的數(shù)的關(guān)系，是逐步用數(shù)表示事物規(guī)律的過(guò)程。因此，數(shù)感的對(duì)象是高度抽象的數(shù)、符號(hào)，不依賴具體的物理因素，對(duì)數(shù)、符號(hào)及其關(guān)系的判斷是完全基于邏輯的。羅素贊成柏拉圖的思想，認(rèn)為符號(hào)是省略了定義后的“或者”“不是”“一切”“某些”之類的話語(yǔ)，并且不指向現(xiàn)實(shí)世界的任何事物。體現(xiàn)在數(shù)感上，從數(shù)量3個(gè)、長(zhǎng)度3米、重量3千克中，都可以抽象出3的概念，而圍繞數(shù)感的估算與計(jì)算，都是基于3這個(gè)數(shù)的。脫離現(xiàn)實(shí)背景的數(shù)的運(yùn)算并無(wú)實(shí)際意義（如3+2=5，而3天+2小時(shí)$5天），因此，數(shù)感最終指向抽象能力的培養(yǎng)。

量感是借助測(cè)量或估測(cè)，產(chǎn)生對(duì)事物可測(cè)量屬性的直覺(jué)認(rèn)知，以解決實(shí)際問(wèn)題。因此，量感的對(duì)象是客觀存在的事物，其最終的培養(yǎng)目的也在于解決實(shí)際問(wèn)題。梁培斌認(rèn)為，必要的測(cè)量經(jīng)歷有利于學(xué)生形成量感，從而進(jìn)一步培養(yǎng)估測(cè)能力，這種能力最終指向?qū)W生應(yīng)用意識(shí)的培養(yǎng)。"例如，測(cè)出一個(gè)正方形的邊長(zhǎng)是3厘米，依據(jù)正方形的面積公式，求得該正方形的面積是9平方厘米。實(shí)質(zhì)上，此時(shí)的運(yùn)算具有一定的物理意義，合理地解決了現(xiàn)實(shí)應(yīng)用中難以直接測(cè)量面積的問(wèn)題。因此，量感最終指向抽象思維的應(yīng)用意識(shí)的培養(yǎng)，以及應(yīng)用價(jià)值的感悟。

（三）問(wèn)題表征方面的區(qū)別

問(wèn)題表征方面，數(shù)感是數(shù)量關(guān)系問(wèn)題中數(shù)及運(yùn)算的表征"強(qiáng)調(diào)如何通過(guò)合理的運(yùn)算求得標(biāo)準(zhǔn)的數(shù)值結(jié)果，是數(shù)量感在運(yùn)算規(guī)律方面的體現(xiàn);量感可作為數(shù)量關(guān)系問(wèn)題中判斷是否合乎情理的原則，強(qiáng)調(diào)如何通過(guò)物理意義構(gòu)建合理的算式（運(yùn)算步驟'是數(shù)量感在邏輯判斷方面的體現(xiàn)。

數(shù)感表現(xiàn)為借助數(shù)、計(jì)數(shù)單位、進(jìn)制等抽象的概念，結(jié)合運(yùn)算法則，合理地輸出結(jié)果（仍為數(shù)'也就是，將問(wèn)題歸結(jié)為“怎么算”。量感表現(xiàn)為通過(guò)對(duì)量的物理意義的理解，構(gòu)建實(shí)際物理含義與算式之間的對(duì)應(yīng)關(guān)系，從而確定合理的運(yùn)算步驟（選取哪些量進(jìn)行怎樣的運(yùn)算'也就是，將問(wèn)題歸結(jié)為“算什么”。例如，對(duì)“物體運(yùn)動(dòng)距離是10米，運(yùn)動(dòng)時(shí)間是2秒，以及其他已知量，求物體運(yùn)動(dòng)速度”的問(wèn)題，借助量感的經(jīng)驗(yàn)性及轉(zhuǎn)換性，構(gòu)建“速度等于距離除以時(shí)間”的運(yùn)算邏輯，以此列出速度的計(jì)算公式^即用10米除以2秒。此時(shí)的運(yùn)算步驟是符合客觀現(xiàn)實(shí)的，通過(guò)量綱檢驗(yàn)可以驗(yàn)證其合理性。在此基礎(chǔ)上，借助數(shù)感，將后續(xù)問(wèn)題表征為距離的數(shù)值與時(shí)間的數(shù)值如何做除法，即10除以2如何依據(jù)法則求得運(yùn)算結(jié)果。此時(shí)，關(guān)注的是利用乘法口訣進(jìn)行數(shù)值求解，而不考慮計(jì)算的實(shí)際意義。直觀地看，量感與數(shù)感的區(qū)別便在于單位是否參與運(yùn)算，量感強(qiáng)調(diào)單位必須參與運(yùn)算，而數(shù)感則不然。

（四）發(fā)展方向方面的區(qū)別

在發(fā)展方向上，數(shù)感最終指向數(shù)的感知能力以及運(yùn)算速度與準(zhǔn)確度的提升，強(qiáng)調(diào)數(shù)量感中合理估算部分的發(fā)展;量感最終指向?qū)ξ锢砹空J(rèn)知的逐步理性化、辨析化，以及測(cè)量與估測(cè)準(zhǔn)確性的提升，強(qiáng)調(diào)數(shù)量感中客觀實(shí)在維度辨析部分的發(fā)展。

數(shù)感的發(fā)展方向有以下兩個(gè)維度：一是數(shù)的關(guān)系，如互質(zhì)關(guān)系、最大公約數(shù)關(guān)系、平方關(guān)系等認(rèn)知的發(fā)展，在基本活動(dòng)經(jīng)驗(yàn)的基礎(chǔ)上形成快速而準(zhǔn)確的感知能力%二是數(shù)的運(yùn)算，如四則運(yùn)算等在快速、準(zhǔn)確方面的發(fā)展。數(shù)感好的學(xué)生對(duì)數(shù)的關(guān)系及數(shù)的運(yùn)算具有敏銳感。例如，給出數(shù)字169，可以快速反應(yīng)它是13的平方數(shù);給出數(shù)字12和15，可以迅速反應(yīng)二者的最大公約數(shù)為3;提問(wèn)“3X5等于多少”，能夠借助乘法口訣快速回答15，而非進(jìn)行5！5！5=15的計(jì)算。

量感的發(fā)展方向也存在兩個(gè)維度：一是提升測(cè)量與估測(cè)的能力%二是提升理解與選擇度量單位的能力，進(jìn)而準(zhǔn)確感知物理量的維度與大小。量感好的學(xué)生對(duì)客觀事物的物理屬性具有敏銳感。例如，可以快速判斷一個(gè)桌面具有長(zhǎng)度、面積、體積、重量等物理屬性，可以合理進(jìn)行測(cè)量，通過(guò)“數(shù)字+單位”的方式表達(dá)感知結(jié)果，并理解長(zhǎng)度、面積、體積之間的關(guān)系。

四、結(jié)語(yǔ)

數(shù)感與量感是由數(shù)量感分化而來(lái)的兩個(gè)概念。在教材內(nèi)容安排以及教學(xué)活動(dòng)設(shè)計(jì)中，二者往往同時(shí)出現(xiàn)：數(shù)感為量感提供理性支持，增加量感的科學(xué)性與嚴(yán)謹(jǐn)性;量感為數(shù)感提供可靠的抽象來(lái)源，為深人理解數(shù)及其關(guān)系提供良好的支撐點(diǎn)。但是，數(shù)感與量感也有所區(qū)別，混淆二者的概念對(duì)培養(yǎng)學(xué)生的數(shù)感與量感是不利的。結(jié)合2022年版課標(biāo)，教師需要準(zhǔn)確把握數(shù)感與量感的共性與區(qū)別，在教學(xué)過(guò)程中對(duì)癥下藥，并逐步深化二者的融合，最終助力學(xué)生數(shù)感與量感清晰且有深度的發(fā)展，從而助力學(xué)生數(shù)學(xué)核心素養(yǎng)的發(fā)展。

（吳立寶，天津師范大學(xué)教育學(xué)部，教授，博士生導(dǎo)師。主要研究方向：教師教育與數(shù)學(xué)教育。高博豪，天津師范大學(xué)教育學(xué)部。主要研究方向：數(shù)學(xué)教育。郭銜，北京師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，副教授，博士生導(dǎo)師。主要研究方向：數(shù)學(xué)教育。）