淺談簡便運算教學策略

羅尖武

數的運算在小學數學課程中占據至關重要的地位，而簡便運算是運算教學中的“重頭戲”，它能充分鍛煉學生思維的靈活性，提高運算的正確率。但由于它的形式多變、方法靈活，因此一直是學生容易混淆和出錯的知識。在教學時，教師要優化教學策略，培養學生簡便運算的能力，使其在運算過程中體會簡算優勢、提升簡算能力。

一、創設情境，培養意識

在日常生活中經常用到簡便運算，教師可以抓住其實用性的特點，創設生活化的問題情境，拉近學生對所學知識的親近感。因此，教師在教學時可以依據教學內容，創造性地使用教材，把枯燥乏味的算式轉化成學生熟悉的生活情境。這樣有利于激發學生的學習興趣，使他們在學習過程中感受到簡便運算與生活的密切聯系，體會到簡便運算在生活中的便利，激發學生簡便運算的意識。

例如，在教學人教版四上“加法運算定律”的相關內容時，教師出示題目：115-99，讓學生用簡便的方法進行運算。此時，教師可創設一個學生喜聞樂見的購物情境，來激活學生的生活經驗，幫助他們厘清算理。在課件中展示情境：“陳熙同學身上有一張100元鈔票和15元零錢，他想買一個99元的書包，該怎樣付錢？售貨員會怎樣找錢？最后陳熙同學身上還剩多少錢？”這樣的問題貼近學生生活，大部分學生都能根據已有的生活經驗進行思考：陳熙會拿出100元給售貨員，售貨員找給他1元，陳熙最后剩下的錢是15+1=16（元）。接著教師讓學生把付款的過程寫成算式：115-99=100+15-99=100-99+15=16。這樣學生就很容易理解這個算式的簡便運算方法了。

又如，在教學人教版四下“乘法運算定律”的相關內容時，教材雖然提供了植樹的情境，但針對乘法分配律給予學生的直觀感受并不明顯，因此筆者把情境改成了學生熟悉的“買校服”情境：“學校購買校服，每件上衣30元，每條褲子25元，買4套這樣的校服，一共多少元？”情境出示后，引導學生進行獨立思考和解答，根據學生回答出的兩種情況，讓他們分別在黑板上寫出算式：（1）（30+25）×4=220（元）;（2）30×4+25×4=220（元）。在展示、交流、分享的過程中，讓學生說出每一步算式的意義，最后教師把兩個算式用等號連接起來：（30+25）×4=30×4+25×4，這樣讓學生在現實情境中對乘法分配律的結構有一個初步的認識。來自于生活的情境創設不僅激活了學生的生活經驗，還使簡便運算在學生的意識中開花結果。

二、數形結合，化難為易

“數缺形時少直觀”，在數學教學時如果能從“形”的角度來呈現“數”，將會使抽象的數學定律、數學性質和數量關系等變得具體、形象、簡單。

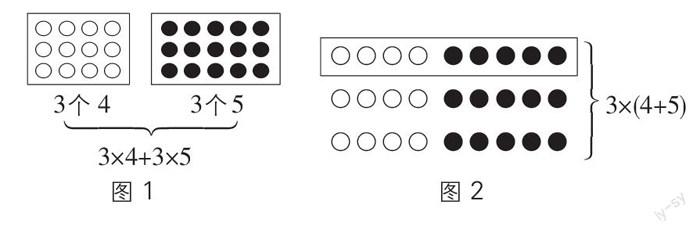
仍以教學人教版四下“乘法運算定律”為例，教師發現乘法分配律這一運算定律較之乘法交換律與乘法結合律更為抽象，單純地創設情境，學生不一定能理解其中的內涵與應用。倘若在教學中適當挖掘教材的潛力，運用數形結合的方式加以呈現，針對乘法分配律建立學生熟知的幾何模型，化抽象為具體，讓學生充分體驗算理，達到對算理的理解和對算法的把握，則這一教學難點將迎刃而解。在此，教師課件出示問題：“六一兒童節來臨之際，陳老師想對教室進行布置，他要在教室里掛3排燈籠，每排燈籠由4個黃色燈籠、5個紅色燈籠組成，一共要買幾個燈籠？”引導學生動手用學具擺一擺，再說出自己的想法。這時學生中出現兩種解題方法：（1）3×4+3×5=12+15=27（個）;（2）（4+5）×3=9×3=27（個）。教師適時追問：“他們是怎么想的？你們看懂了嗎？能在學習單的點子圖上畫一畫、圈一圈，再說說你們的想法嗎？”學生結合圖形操作（見圖1、2）充分交流后，再進行匯報展示。生：“方法一是分別求出黃色燈籠和紅色燈籠的個數再相加;方法二是先求一排有多少個燈籠，再求三排一共有多少個。”借助直觀圖形的畫一畫、圈一圈，學生可以快速發現3×4+3×5=（4+5）×3，兩個算式都能準確求出燈籠的總數。這樣，采用數形結合的方式讓學生在腦海里形成乘法分配律的基本模型，那么學生對于乘法分配律的認知會更加深刻。

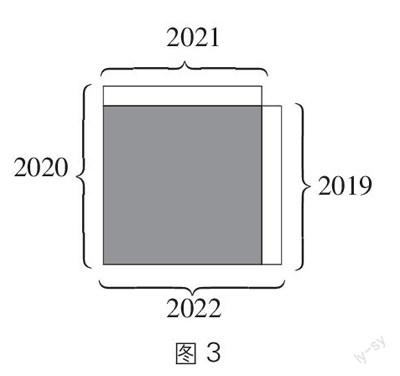
又如，教師出示算式：2021×2020-2022×2019，要求學生用簡便計算的方式解這道題。通過觀察發現：兩個積相減，其中沒有相同因數，但幾個數都非常接近。這時教師可引導學生用面積圖的形式畫出示意圖（如圖3），并借助示意圖進行思考：要求兩個乘積的差就是求兩個長方形的面積差，去掉公共部分的面積，剩下的兩個小長方形的面積差就是原來兩個長方形的面積差。所以2021×2020-2022×2019=2021×1-2019×1=2。

教師在教學簡便運算的方法時，除了引導學生要牢記運算定律、運算性質，還要讓他們仔細觀察運算符號、數據特點。在一定的條件下，如果能合理地將運算與圖形結合思考，也能化難為易，化抽象為形象。

三、錯題解析，加深理解

教師要在教學中把學生的錯誤作為一種寶貴的教學資源，并利用和發掘其中蘊含的教育價值。筆者在教學實踐中發現學生在簡便運算中經常出現以下三種錯誤：（1）325×99=325×（100-1）=325×100-1=32500-1=32499;（2）25×4÷25×4=（25×4）÷（25×4）=100÷100=1;（3）325-25+75=325-（25+75）=225。我們應對以上三種錯誤進行充分解析，了解學生是怎么想的，為什么會這樣想，代入學生的思維，找出出錯的結點，進行深入分析，使他們明白錯誤的原因。在第一個算式中，乘法分配律的運用出現錯誤，應為325×（100-1）=325×100-325×1=32500-325=32175。第二個算式的解法忽視了整體的運算順序，把注意力集中在湊整上，忽略了同級運算時進行簡便運算必須要“帶符號搬家”，因此該題的簡便運算應為25×4÷25×4=25÷25×4×4=1×4×4=16。第三個算式的解法錯誤是由于“湊整思想”反復強調、反復訓練，結果導致很多學生看到能湊整的數字就會產生條件反射，導致他們盲目湊整，忽視了本身的運算順序。此時教師可以加強對比練習，以第三個算式的錯誤資源為例，出示類似的算式：245-25+75。首先教師應引導學生理解結合律不是任意兩個數都可以結合的，同時結合算式創設具體的情境：“大佛寺里原來有游客245人，出去了25人，又進來75人，現在有游客多少人？”讓學生根據情境理解算式本身的意義。接著與算式245-25-75進行對比研究，讓學生根據教師創設的原有情境進行情境的改編，感受兩個算式之間的差異，深刻理解算式245-25+75的正確運算方法。因此，教師應引導學生收集、整理平時作業中出現的一些典型錯例，在錯誤中反思、總結，從而提高解題效率和準確率。

（作者單位：福建省羅源縣鳳山小學 本專輯責任編輯：宋曉穎）

編后記

數的運算是小學數學知識體系中的重要部分，也與其他類別的數學知識有著密切的聯系。因此，如何有效提升學生的運算能力，構建深入的、易為學生所接受的運算教學課堂，是廣大數學教師所關注的要點之一。本專輯的文章對此做了初步的探究，有助于一線教師豐富運算教學經驗。