問題提出理念引領下的數學游戲課教學
郭芬香
一、數學游戲課
“數學游戲”在《英國簡明百科全書》中,條目是
“mathematical recreations”,定義為“利用數學知識的流行的娛樂活動”。我們把一些包含數學原理并使用數學知識或方法的游戲歸類為數學游戲。這不僅是一場游戲,游戲中還包含著數學問題,因此玩游戲的人可以獲得數學活動經驗,并在不知不覺中掌握數學知識、思想和方法。
數學游戲課是借助益智玩具,以數學游戲為基本活動的學習過程。通過直觀操作和數學推理,在學具的幫助下邊玩邊想,在動手實踐中豐富活動經驗,玩中學、做中思,培養學生的學習興趣;在游戲中進行深層次的思維訓練,培養學生的數學能力,啟迪智慧,開發潛能。
二、問題提出
對于數學教育中的問題提出,蔡金發教授認為,應該是支持教師和學生的具體活動,使他們能夠根據特定的情境(即問題背景或情境)形成或重新形成數學問題或任務。在這個定義中,蔡教授對“問題”或“任務”進行了更廣泛的分析,包括任何可以提出的數學問題以及根據問題可以提出的任何數學任務。
三、基于問題提出的數學游戲課的基本結構
“基于問題提出的數學游戲課”指將問題提出理念運用于數學游戲課的教學中,通過提出問題,大膽猜想,實踐操作驗證或推理論證,解決問題,發展問題意識和創新能力。
四、“漢諾塔”游戲
教學目標:
第一,以“漢諾塔”游戲為載體,培養學生依據材料從不同角度提出數學問題的能力。
第二,孩子們在猜想、驗證(操作、推理、規律)過程中解決問題,培養解決問題的能力,發展創新思維。
第三,借助數學游戲,激發學習數學的興趣。
教學設計:
(一)利用傳說,提出問題
“漢諾塔”游戲源于印度傳說,卻是法國數學家最先改編成數學問題并進行研究。對于傳說本身,就包含著許多的問題因素。
1.閱讀材料,形成問題
課始,教師出示文字材料:法國數學家愛德華·盧卡斯編寫過一個印度的古老傳說:在印度北部的圣殿里,三根寶石針被插入一個銅盤中。印度教的主神梵天創造世界的時候,在其中一根針從下到上穿好了由大到小的64片金片,這就是所謂的漢諾塔。不論白天黑夜,總有一個和尚在按照下面的法則移動這些金片:一次只能移動一片,無論在哪根針的上面,小片必須在大片上面。
學生看文字材料,獨立思考寫下自己認為和數學有關的1~2個問題。在自主提問階段,經過獨立思考之后,學生將相關數學知識內化,以達到個性化的學習狀態。
【設計意圖:以古老的印度傳說引入,更能激發學生的數學學習興趣,增加好奇心,對課堂學習充滿期待。根據傳說提出問題,需要學生先仔細閱讀,提高學習的
效率。】
2.篩選問題,達成共識
在獨立提問基礎上,經過小組討論,整理出最想討論解決的3個問題。之后各小組派代表講2個問題,層層篩選,共形成了以下9個問題:
(1)為何是3根針?
(2)為何是64片?
(3)為何一次只能移一片?
(4)為何小的要在大的上面?
(5)為什么法國的數學家要編寫印度的傳說?
(6)不按法則移動會產生怎樣的后果?
(7)要移幾次(多久)?
(8)為何叫漢諾塔?
(9)漢諾塔是誰發明的?
【設計意圖:通過組內篩選,小組成員達成共識,剔除部分與本課學習關系不大的問題,使數學問題更集中指向本課學習,使問題更好地為本課教學服務。】
3.根據問題,分類整理
通過對數學問題的分類,抽象出問題的共性特點,從解決一個問題到一類問題進行延伸。
師:同學們有9個問題要解決,我們該怎么做才能系統地解決這么多的問題?
生:分類。
師:你認為這些問題可以分成幾類?以小組為標準進行分類。
反饋后統一結果:計算類(7);規則類(1、2、3、4、6);其他類(5、8、9)。
【設計意圖:在分類過程中探尋標準進行判斷,在討論、交流中不斷修正思維,層層推進,發展了合作交流和語言表達能力。】
(二)依托問題,大膽猜想
在分類基礎上思考計算類問題,體會不易。
師:第7個問題能解決嗎?請你猜一猜到底要移
多久?
生1:應該要很長的時間。
生2:幾億次吧?反正很久很久……
【設計意圖:在分類基礎上進行猜想,讓學生體會解決數據較大問題之不容易,從而用化繁為簡進行解決。】
(三)合作探究,驗證猜想
將復雜問題簡單化,是數學學習的基本方法。運用規則操作驗證,理解算理,在推理中尋找規律,最終解決問題。
1.實踐體驗,操作驗證
根據移動規則,運用學具探索,增加活動經驗。通過思考相關聯步數,感悟規律。
師:想要解決這么復雜的問題,我們可以怎么辦?
生:化繁為簡,移一移漢諾塔,動手操作一下。
師:傳說中是64片,老師提供的是5片,請你思考,該從幾片開始研究?為什么?
生:從3片開始研究,2片很簡單,只要3步(生移);3片要移7步,要復雜些。
師:3片都會移嗎?那4片要移幾次?(生說15次)
師:同桌合作,1人移,1人記錄,并仔細觀察思考有沒有移錯。先移動3片,學生都會移了,再研究移動4片,請關注移動的次數,并思考移動3片和移動4片有什么關聯?(2人合作操作)
師:誰能概括性地來說一說移動3片和4片之間有什么關聯?
生:從移動3片到4片是3片的步數乘2再加1,師板書:7×2+1=15。
師:在移動過程中如何看出7×2+1?請在漢諾塔上演示。
生:先讓3片移到中間桿要用7步,最大地移到目標桿加1步,最后把中間的3片移到目標桿又是7步(7+1+7),同時演示7+1+7的過程。
【設計意圖:根據規則運用學具進行操作體驗,在體驗中感悟移動3片和4片之間的聯系,突破難點,為尋找規律打下伏筆。】
2.回顧反思,推理驗證
回顧課堂,在操作過程中積累了經驗,通過推理,尋找漢諾塔的移動規律。
(1)在回顧交流中探尋規律
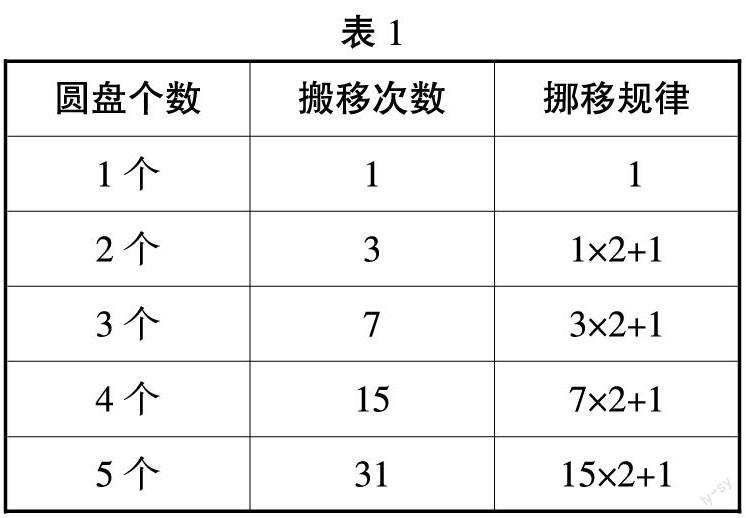
教師出示表格,根據表格,說一說移動5片要幾次。(見表1)
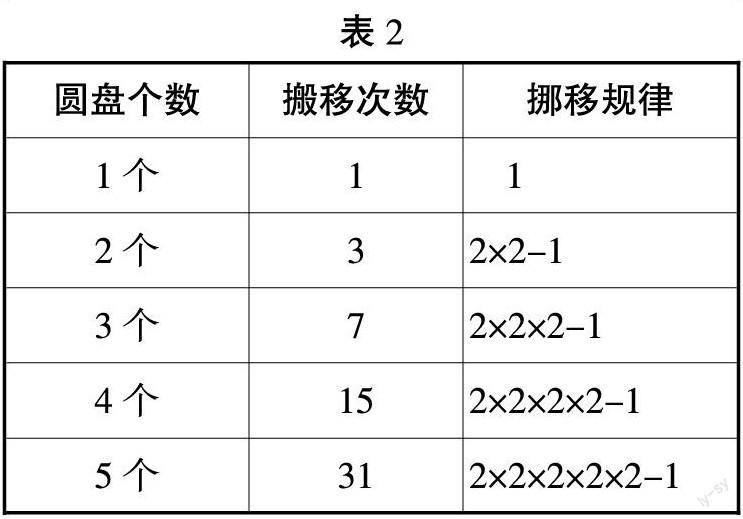
如果教師把挪移規律稍微改動一下,你看得懂嗎?5個圓盤該怎么表示?(見表2)
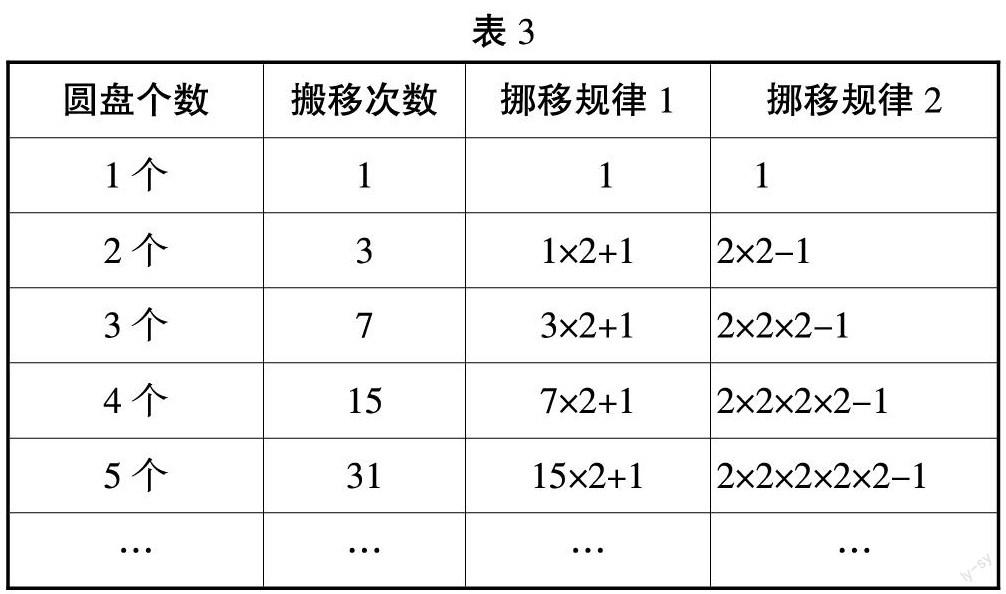
根據表1、表2,完成表3:
【設計意圖:根據移動3個、4個圓盤的操作,在經驗積累的基礎上尋找搬移次數的規律。在規律探究中發現移動5個、6個,甚至更多個圓盤的移動規律。】
(2)在猜想估算中探尋規律
猜一猜移完20片要幾次?學生猜后教師說,移完20片要100萬次,同時出示表格(略)。
10個圓盤超過1000次,20個圓盤超過100萬次,再猜,30個幾次?
生:超過1億。
師:對,100萬后面大概還要加幾個0?(學生說3個0)是的,30個圓片最少挪移1073741823次,超過10億次,太不可思議了。PPT出示表格(略)
師:如果一天工作8小時,一秒挪移一次,30個圓盤要多久才能完成挪移?
師:先除以60變成分鐘,再除以60變成小時,再除以24變成天,再除以365變成年,這些事情計算機已經算好。
一天工作8小時=28800秒
1073741823÷28800≈37283(天)
37283÷365≈102(年)
師:如果僧侶不休息地去做這件事,大概需要幾年?(34年)
【設計意圖:從移動10個到30個圓盤的移動次數,孩子們在猜想驗證推算活動中體驗30個圓盤的移動次數,進而體會完成這件事需要的時間有多漫長。】
3.依據材料,尋理論證
64個圓盤的移動規律,在學生現階段還難以根據推理計算。在文字材料中尋求證據,進行論證。
師:再看一段文字材料。
斗轉星移,梵天寺的僧侶們換了一代又一代,可是到現在那64個金盤子好像從來沒移動過似的。為了那個神圣的誓言,僧侶們確實從來沒有停止過工作,世界也依然很美好……時間一下到了20世紀40年代末的一天,大洋彼岸的一幫人搞出了電腦這個玩意兒,用電腦計算了移動64個金盤子所需要的時間:假如每次移動耗時1秒,移動64個盤子到第三根柱子需要的時間是264-1=18446744073709551615秒,換算成時間是5845.54億年;看來僧侶們的任務任重道遠,因為地球到目前為止才46億年。
【設計意圖:與前面的傳說相呼應,更好地體現了漢諾塔傳說的研究價值,使孩子們感受到編寫神話者的
智慧。】
(四)課堂總結,明確目的
出示文字材料:提出一個問題通常比解決一個問題更重要,因為解決問題可能只是一種教學或實驗技能而已。而提出新問題、新可能性并從新的角度看待舊問題需要創造性的想象力,這標志著科學的真正進步。
——愛因斯坦
【設計意圖:發現并提出問題比解決問題尤為重要,從而激勵孩子們提出更多的好問題。】
教后反思:
漢諾塔問題具有很高的研究價值,也是一種益智游戲。一般課堂都讓學生根據游戲規則,尋找規律,解決實際問題,學會有條理地思考,獲得成功體驗這一路徑開展教學。本課打破了教師原有的教學模式,在問題提出理念引領下,讓學生經歷提問問題、分析問題和解決問題的過程。真正在課堂教學中落實了動手實踐、自主探究、合作交流這一課程理念。
(一)在問題引領中學習
拓展性數學游戲課程的教學目標不僅可以激發學生的學習興趣,培養學生的動手操作能力和發展思維,還可以培養學生的創新意識。發現和提問是數學課程的目標之一,在教學中培養學生的課堂提問能力也是培養創造性思維的有效途徑。在“漢諾塔”的教學中,利用傳說這個載體,鼓勵每個孩子提出問題。盡管一開始有的孩子提的問題對于本課的學習沒有價值,但在提問的過程中孩子們積極思考,參與其中,真正體現了“不同的人在數學學習中得到不同的發展”這一課標理念。之后,教師篩選小組中的所有問題,并選擇有價值的問題進行討論和研究解決。在小組合作過程中培養合作意識,發展了批判性思維。在用漢諾塔操作活動時,又圍繞核心問題“誰能概括性的來說一說移動3片和4片之間有什么關聯?”引領學生進一步思考,從而發現移動規律。
(二)在互動交流中體現學生立場
促進學生有效提問的前提是堅持學生的地位,相信學生能夠學習,構建寬容、尊重、和諧的師生關系和安全、溫暖的課堂氛圍。因為當你安全時,你會平靜,當你平靜時,你會明智。這是引導學生獨立提問的生態基礎。課始,教師讓學生自主提問后,在組內進行互動交流,篩選有價值的問題,教師沒有參與其中,這是建立在充分信任基礎上的自主學習。實踐證明,學生有能力對自己所提的問題進行甄選,及時放手調動了學生學習的主觀能動性,發展了高階思維能力。
(三)提出問題比解決問題更重要
學貴有疑,小貴則小進,大疑則大進。“懷疑”是人類打開宇宙之門的金鑰匙,提出問題比解決問題更重要。從課中可以看出學生的問題非常多,篩選后還剩下一部分,一節課中沒有辦法全部完成。教師在和學生交流的過程中挑選了部分問題進行解決。正如課終所言“今天這節課我們提出了很多問題,也解決了很多問題,如果你能在解決問題后發現新的問題,當你解決的問題越多,那你提問題就會越來越難,每次想出新的問題,那新的可能性又要發生了。就像剛才有同學提到的第5個問題,印度人還只是當成一個傳說的時候,法國人已經提出數學問題了。”這樣的課堂培養的是學生創新思維能力,也是我們應該追求的目標。
五、啟示
“漢諾塔”這一拓展性游戲內容,研究價值不僅限于益智,更能培養學生的創新思維能力。整堂課以問題引領著課堂方向和節奏,通過猜想驗證,逐步邁向深入。因此,在數學游戲課中,運用問題提出理念進行教學,不僅能激發學生的數學學習興趣,更發展了學生的創新思維,真正實現教學效益的最大化。
參考文獻:
蔡金法,姚一玲.數學“問題提出”教學的理論基礎和實踐研究[J].數學教育學報,2019(4).

