混合通信拓撲車隊一致性分布式預測控制

余世明,李 壯2,陳 龍,何德峰

(1.浙江工業大學 信息工程學院,浙江 杭州 310023;2.蚌埠學院 電子與電氣工程學院,安徽 蚌埠 233030)

隨著國民經濟與工業科技的迅速發展,汽車行業得到大力發展,但車輛過多和駕駛員對道路環境感知能力不足等因素會帶來交通堵塞和意外事故等問題。車輛隊列一致性協同控制通過調整合理安全間距,可提高車輛燃油經濟性和道路流通效率,在緩解道路交通壓力、實現節能以及提高交通流率和安全性等方面具有重要的作用[1-8]。網聯車隊穩定性可通過協同自適應協同控制保證,通常需要兩車基于車載傳感器所測量的局部信息進行交互,即每輛車可接收到來自相鄰前車的狀態信息,但當車隊規模增大時,整個車隊對干擾的敏感度也隨之增強,則車隊協同控制會受到一定影響[9-10]。因此,車隊系統的通信結構對于協同控制有著很大作用。在網聯車隊中通常存在車輛模型耦合、約束條件非線性以及對應的物理約束,如速度和加速度等,使得車隊協同控制器更難設計。其中,由于分布式模型預測控制不僅可顯式處理非線性約束問題和隊列通信等問題,而且可以使隊列系統滿足良好的控制性能[11-16],從而被眾多學者廣泛學習。文獻[11]考慮帶有雙向通信的車輛隊列非線性系統,設計分布式算法使得隊列達到控制性能;文獻[13]設計分布式MPC控制器解決車輛單向通信問題,并使得隊列滿足穩定性;文獻[16]建立車輛縱向動力學,考慮在多種不同復雜程度的單向通信拓撲下對假設軌跡與預測軌跡的差值懲罰,并設計分布式控制策略,使得車輛之間達到期望間距,滿足一致性。上述研究中,車隊協同控制采用單一通信方式,設計相應控制器使系統滿足一致性性能,但在考慮大規模車隊系統時,跟隨車輛接收頭車狀態信息會越來越困難,則單一通信方式存在一定局限性,不適用于大型車隊協同控制。在車輛隊列現有工作中,針對協同控制提出了一些其他策略,如考慮把隊列控制問題轉換為設計一致性問題解決[17-22]。文獻[17-18]運用線性化動力學模型,分析系統穩定性,利用恒定車間距設計非線性分布式一致性協議,使得隊列系統終態達到一致;文獻[19-20]建立三階非線性縱向偏差動力學模型,其安全間距與車速有關,設計分布式一致性算法,確保隊列系統滿足一致性;文獻[21-22]根據車頭時距策略,設計分布式一致性縱向控制器保證車隊系統穩定性和一致性。上述研究工作大多是基于一致性問題設計分布式控制器,并應用到車輛隊列系統中,但相鄰車輛之間的車間距不滿足弦穩定性。另外,穩定性證明所應用的線性化方法在系統出現不確定性時會降低精度,在一定程度上影響控制效果。當所考慮的車隊系統性能指標是非凸時,僅用傳統MPC較難處理,且系統穩定性無法保證。為解決此類問題,許多學者進行了相關研究,文獻[23]提出構造穩定性收縮約束,建立閉環系統穩定性和優化問題遞推可行性;文獻[24]提出基于Lyapunov函數的穩定性約束,用來確保系統穩定;文獻[25-26]采用耗散性和對偶性方法,但通常所研究的車隊系統是非線性的且存在約束條件,這類方法存在局限性。上述多數工作僅考慮了單個系統,以車輛隊列為對象的工作較少,文獻[27]基于雙層控制策略設計車輛隊列協同控制算法,但單車系統穩定性無法得到保證。

筆者所提出的分布式雙層策略可有效解決這類問題,且使得系統滿足相應的控制性能。首先,在混合拓撲通信下,考慮具有狀態和控制輸入約束的非線性車隊系統;然后,應用MPC、滾動時域策略以及構造穩定收縮約束建立車隊系統穩定性、動態一致性優化問題,以遞推可行性以及弦穩定的充分條件;最后,通過7輛車的數值仿真驗證所提策略的有效性。

1 問題描述

考慮車隊系統由n輛車組成,其中1表示車隊中第1輛車。令車隊中每輛車i(i=1,2,…,n)可以接收到任意與其通信車輛j(j≠i)所傳遞的信息。在初始時刻,車隊跟蹤參考軌跡,其軌跡信息為(pdes,vdes),同時所有跟隨車輛i接收到期望速度vdes;在其他時刻,第1輛車跟蹤期望軌跡,其他車輛i(i=2,3,…,n)跟蹤前車i-1,并接收與本車通信車輛j(j∈Ωi)的狀態信息。假設車輛行駛在平坦的公路上,模型不存在干擾,且通信性能良好。

車輛i(i=1,2,…,n)的位置和速度由pi和vi表示,定義車輛i相對位置偏差ep,i=sdes-si-(i-1)d和速度偏差ev,i=vi-vdes。則車輛i的縱向偏差離散時間模型[16]為

(1)

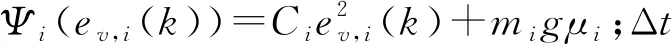
umin,i≤ui≤umax,i

(2)

式中:umin,i<0;umax,i>0,且是有界的。通常情況下,車輛剎車性能好于加速性能,即控制輸入滿足|umin,i|≥|umax,i|以保證車輛良好的剎車性能。假設系統存在平衡點(xi,s,ui,s)滿足xi,s=fi(xi,s,ui,s)。對于每輛車i而言,其狀態變量可表示為xi(k)=[ep,i(k),ev,i(k)]T。為了書寫方便,將式(1)簡記為

xi(k+1)=fi(xi(k),ui(k))

(3)

定義1當期望速度vdes在k=0時刻發生階躍變化時,控制目標是車隊中每輛車的狀態誤差關于原點是漸近穩定的,則稱隊列系統具有內部穩定[13]。

定義2當期望速度vdes在k=0時刻發生階躍變化時,控制目標是車隊中每輛車的狀態關于原點是漸近穩定的,且閉環系統式(3)的位置誤差滿足以下關系式

(4)

對任意i=2,3,…,n存在βi∈(0,1),則稱為弦穩定[13]。

假設車隊中包含n輛車,將每輛車視為一個節點,該車隊中所有車輛表示為一組元素集合NG={1,2,…,n}。車輛間的通信方式可由一組有權重單向圖G=(NG,εG,A)表征。其中εG?{(i,j):i,j∈NG,j≠i}表示為邊緣集。A表示為鄰接矩陣,鄰接矩陣A用于描述在跟隨車輛的有向通信拓撲,其被定義為A=[aij]∈Rn×n,矩陣中每個元素aij可表示為

(5)

式中:(j,i)∈εG為在節點i和節點j之間存在一條有向路徑;aij為節點i從節點j接收到狀態信息。而aji是與aij不同的通信連接方式,其表示節點j從節點i接收到狀態信息。若從節點i到節點j存在一條路徑,其中節點i∈NG與節點j∈Ωi是連通的,Ωi表示為節點i的鄰居節點集合,其集合Ωi={j|aij=1,j∈NG},對偶集合Θi={j|aji=1,j∈NG},對于無向圖有Ωi=Θi。

對于?i,j∈NG×NG,節點i與節點j是連通的,則圖G是強連通的。當存在根節點i∈NG,?j∈NG,在一條從節點i到節點j的路徑,則有向圖包含一條有向生成樹,其中有向樹是指它除了根節點之外,每個節點都只有一個父節點,而根節點沒有父節點,但它有一條路徑通往其他所有節點。其是隊列協同控制達到一致性的條件之一。

筆者目標是針對非線性車隊系統協同一致性問題設計分布式分層控制,使得閉環系統滿足穩定性和對應的編隊隊形,保證安全性,同時使得車隊系統狀態達到一致穩態。

2 車隊一致性DMPC

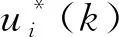
為了使動態一致性性能在預測時域內最小化,定義動態一致性目標函數為

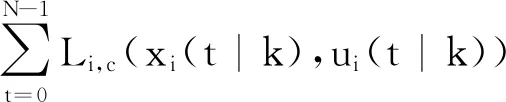
(6)

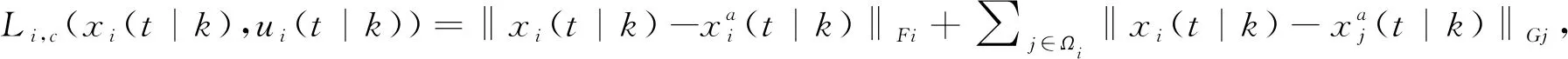
問題1:

(7)

s.t.xi(t+1|k)=fi(xi(t|k),ui(t|k))

(8)

(xi(t|k),ui(t|k))∈Xi×Ui,t=1,2,…,N

(9)

xi(0|k)=xi(k),xi(N|k)∈Xi,T,i=1,2,…,n

(10)

(11)

Ji(xi(k),ui(k))≤φi(xi(k),λi)

(12)

考慮車輛隊列系統跟蹤性能,定義單車穩定性目標函數為

(13)

式中:Ji(xi(k),ui(k))=xTi(N|k)Pixi(N|k)+∑N-1 t=0xTi(t|k)Qixi(t|k)+uTi(t|k)Riui(t|k);矩陣Qi=QTi>0,Ri=RTi>0,Li:Xi×Ui→Ξi和Ei:Xi∈Ξi是連續有界的,Xi和Ui為凸集。則求解優化問題為

問題2:

(14)

s.t.xi(t+1|k)=fi(xi(t|k),ui(t|k))

(15)

(xi(t|k),ui(t|k))∈Xi×Ui,t=1,2,…,N

(16)

xi(0|k)=xi(k),xi(N|k)∈Xi,T,i=1,2,…n

(17)

(18)

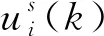
構造收縮約束函數,φi定義為

(19)

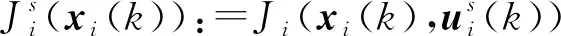
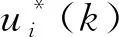
考慮問題1在k時刻可行,則根據滾動時域控制原理,控制律表達式為

(20)

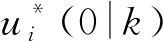
(21)

具體步驟如下:

步驟1初始化(k=0)為

1) 在k=0時刻,車輛i(i=1,2,…,n)接收參考速度vdes,且φi(xi(k),λi)為無窮大。此時,第1輛車求解問題1,且不考慮約束式(11),并將求得的最優狀態x*1,1(t|0)傳遞給后面所有跟隨車輛i(i=2,3,…,n),并將最優控制輸入序列作用到本車系統。

2) 對于車輛i(i=2,3,…,n)接收由第1輛車傳遞的狀態x*1,1(t|0),t∈[0,N],此時求解問題1,并用約束為

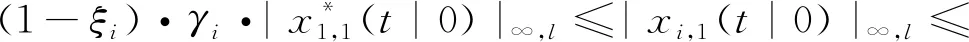
(22)

步驟2迭代(k=1,2,…),每輛車執行過程為

1) 車輛i(i=2,3,…,n)接收來自與車輛i相互通信的車輛j(j≠i,j∈Ωi),所假設的狀態信息。

2) 此時先求解問題2,用于更新φi(xi(k),λi),再求解問題1時,隊列系統增加額外約束條件,對于第1輛車有

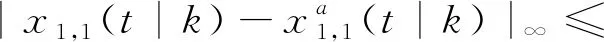
(23)

對于車輛i(i=2,…,n-1)有

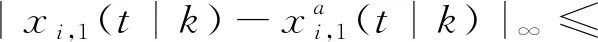
(24)

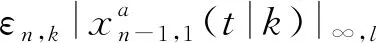
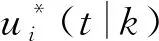
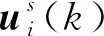
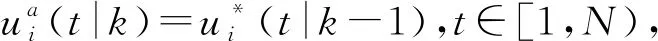
3 穩定性與弦穩定

假設1在終端不變集Xi,T內存在局部控制律ui=κi(xi)滿足κi(xi)?Ui和Ei(fi(xi,κi(xi))-Ei(xi)≤-Li(xi,κi(xi)),?xi∈Xi,T。

引理1存在以下參數條件成立時,表達式為

(25)

則閉環系統位置誤差滿足式(11),其中參數(αi,εi-1,k,εi,k)∈(0,1)[16]。

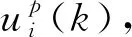
定理1如果假設1成立,對任意給定λi≥0,優化問題1在Xi,N中滿足遞推可行性,進而Xi,N是閉環系統(21)的不變集。

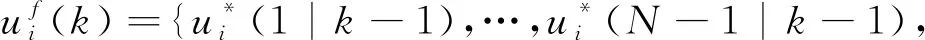
(26)

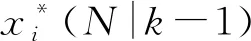
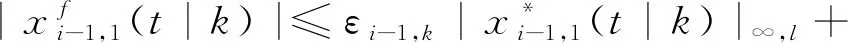
(27)

對式(27)變換得

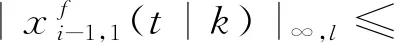
(28)

應用三角不等式和約束式(24)得

(29)

可見文獻[13]引理3,并由初始化時刻約束式(22)得

(30)

根據式(27～30),并將式(28)代入式(29)得

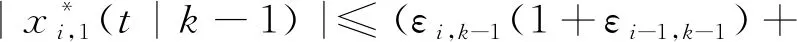
(31)

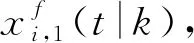
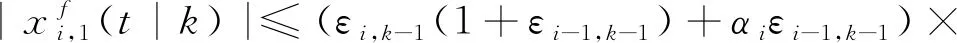
(32)

把式(28)代入式(32)可得

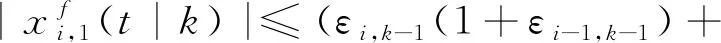
(33)

得不等式(33)有界,且滿足

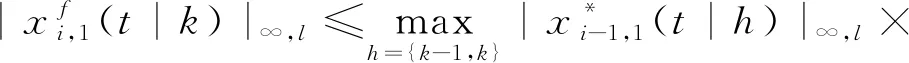
(34)

(35)

考慮控制序列(26),可得

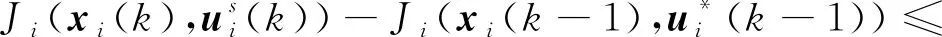
(36)

根據式(35)和假設1,式(36)化簡可得

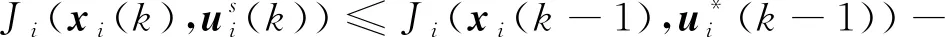
(37)

定理2如果假設1成立,且問題1在初始時刻存在可行解,則對給定λi∈[0,1),則xi,s是閉環系統式(21)在Xi,N內漸近穩定平衡點,且Xi,N是車輛i閉環系統的一個吸引域,XN=X1,N×X2,N×…×Xn,N為整個車隊閉環系統的一個吸引域,且若約束式(22～24)成立,則車隊系統滿足弦穩定。

證明對任意給定λi∈[0,1)優化問題在初始時刻是可行的,根據定理1可知該優化問題在k時刻存在可行解。

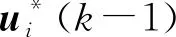
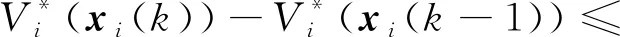
(38)

將式(37)代入式(38),并考慮假設1,整理得

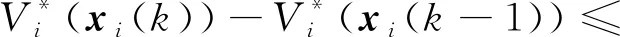
(39)

由于λi∈[0,1),且Li(xi,ui)為正定函數,所以值函數沿著閉環系統(21)的軌跡是嚴格單調遞減的。又因為Ji(xi,ui)是平衡點的正定函數,從而平衡點是閉環系統式(21)在Xi,N內漸近穩定平衡點。Xi,N是車輛i閉環系統的一個吸引域,同理可得XN則是整個車輛隊列閉環系統的一個吸引域。

問題1在任意時刻存在可行解,且閉環系統式(21)關于平衡點漸近穩定。由上述優化問題可行推導過程可知,聯立式(22～24),滿足不等式(4),因此可建立閉環系統的弦穩定。

4 仿真驗證與結果分析

為驗證筆者控制策略可在任意混雜通信拓撲結構下車隊系統滿足穩定性,實現一致性穩態,同時使得車隊系統在運動過程中滿足隊形約束,保持安全車間距離,達到控制性能。利用7輛同質車組成的車隊,驗證筆者策略有效性,其中混雜通信拓撲如圖1所示。

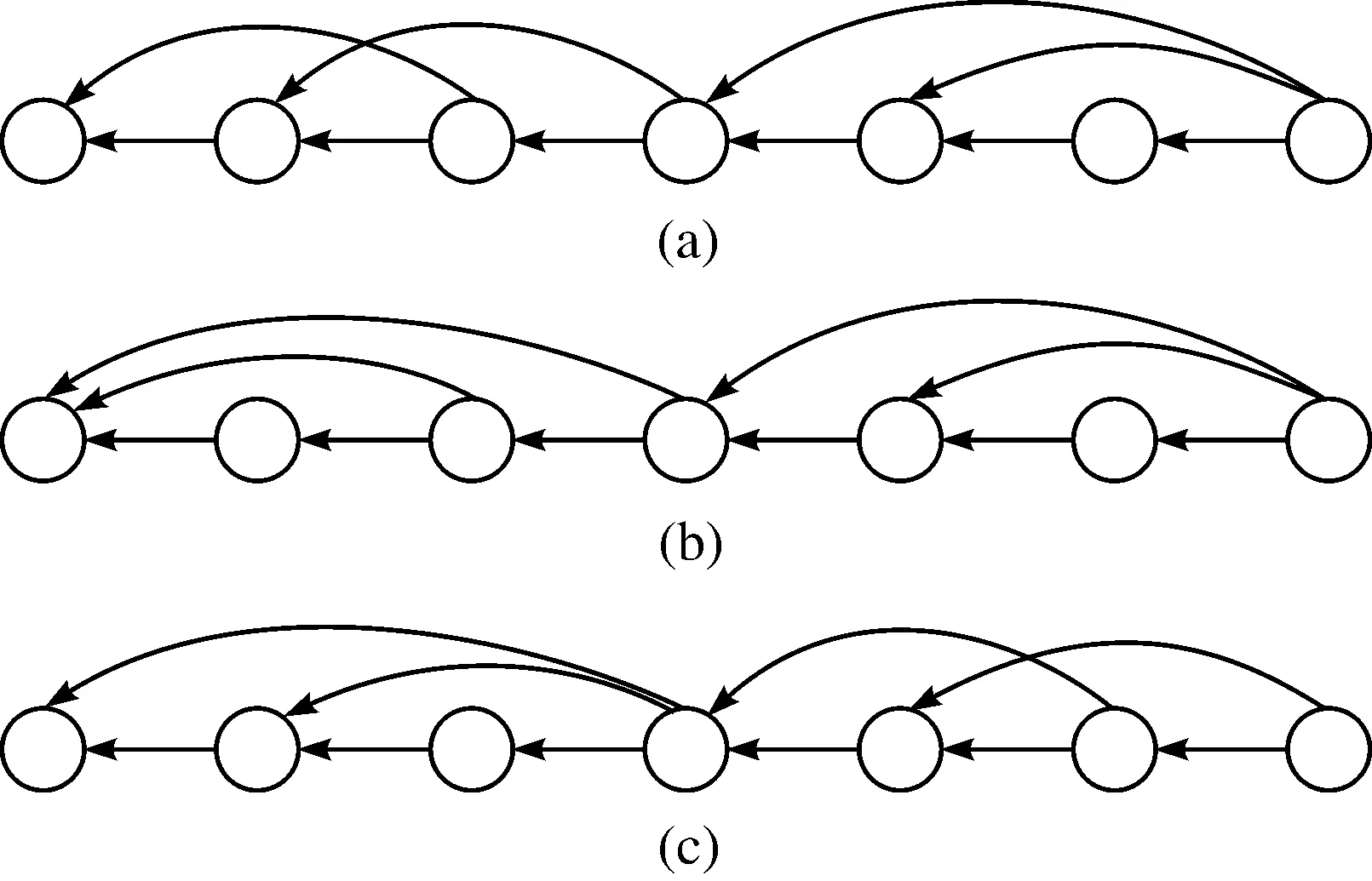
圖1 混合通信拓撲Fig.1 Mixed communication topologies

優化問題預測時域N=12,算法中初始時刻k=0,期望速度vdes從19 m/s增加到20 m/s,車隊跟蹤新的期望速度,確保安全車間距離,直到速度誤差為0,車隊中各車速度相同,且相對期望位置誤差為0。在k=0時,各車相對位置誤差為0,速度誤差為-1 m/s。式(13)和式(6)中懲罰權重取值分別為Qi=diag(0.5,2),Ri=1×10-5,Fi=[2,0;0,2],Gj=[2,0;0,2];車輛參數選取為mi=1 035.7 kg,Ci=0.99 N·s2·m-2,ri=0.30 m,μi=0.015 5,ηi=0.965,i=1,…,7。控制輸入ui的最小值和最大值分別為umin,i=-3 500 N,umax,i=3 500 N,其體現加速度取值,收縮函數(10)中λi=0.8。

系統(1)在平衡點(xi,s,ui,s)處線性化模型求解LQR問題得終端罰函數Ei(xi)=(xi-xi,s)TPi(xi-xi,s)和局部控制器κi(xi)=Ki(xi-xi,s)+ui,s,其中平衡點為(xi,s,ui,s)=(0,0,48.908 7),終端域、矩陣和增益分別為Xi,T={xi∈Ξ2:Ei(xi)≤0.154},Pi=[9 054.705 7,432.710 8;432.710 8,42.313 0],Ki=[134 573.070 9,13 159.336 0]。

4.1 車隊一致性控制比較

在圖1(a)通信拓撲下,首先考慮一致性目標函數式(6),求解問題1用C-MPC表示。應用筆者所提控制策略,求解雙層優化問題記為DH-MPC,其中優化問題約束為式(8～11),參數選取同上文所述。對7輛車組成的車隊進行比較仿真。C-MPC與DH-MPC狀態曲線變化如圖2所示。由圖2可知:當只考慮動態一致性目標(C-MPC)時,車隊系統出現失穩問題,未能滿足跟蹤穩定性,且狀態未達到一致穩態。而筆者提出的分布式雙層策略(DH-MPC)使得車隊系統實現跟蹤穩定,狀態收斂于一致性穩態,且在車隊行駛過程中滿足隊形關系,即弦穩定,同時車輛間保持安全間距,有效地實現車隊協同控制。

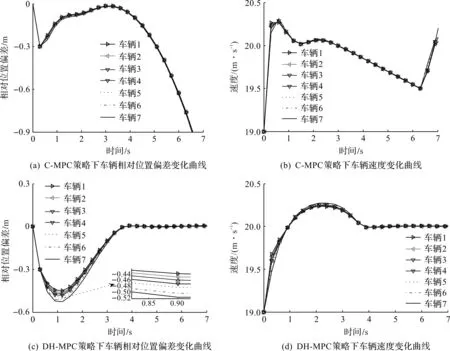
圖2 C-MPC與DH-MPC狀態曲線變化Fig.2 State curves of C-MPC and DH-MPC

4.2 車隊一致性控制

為了驗證分布式雙層策略在任意通信拓撲下使閉環車隊系統式(21)滿足跟蹤穩定性和狀態一致性,并實現車隊協同控制,考慮圖1(b,c)兩種混合通信拓撲,仿真結果如圖3所示。

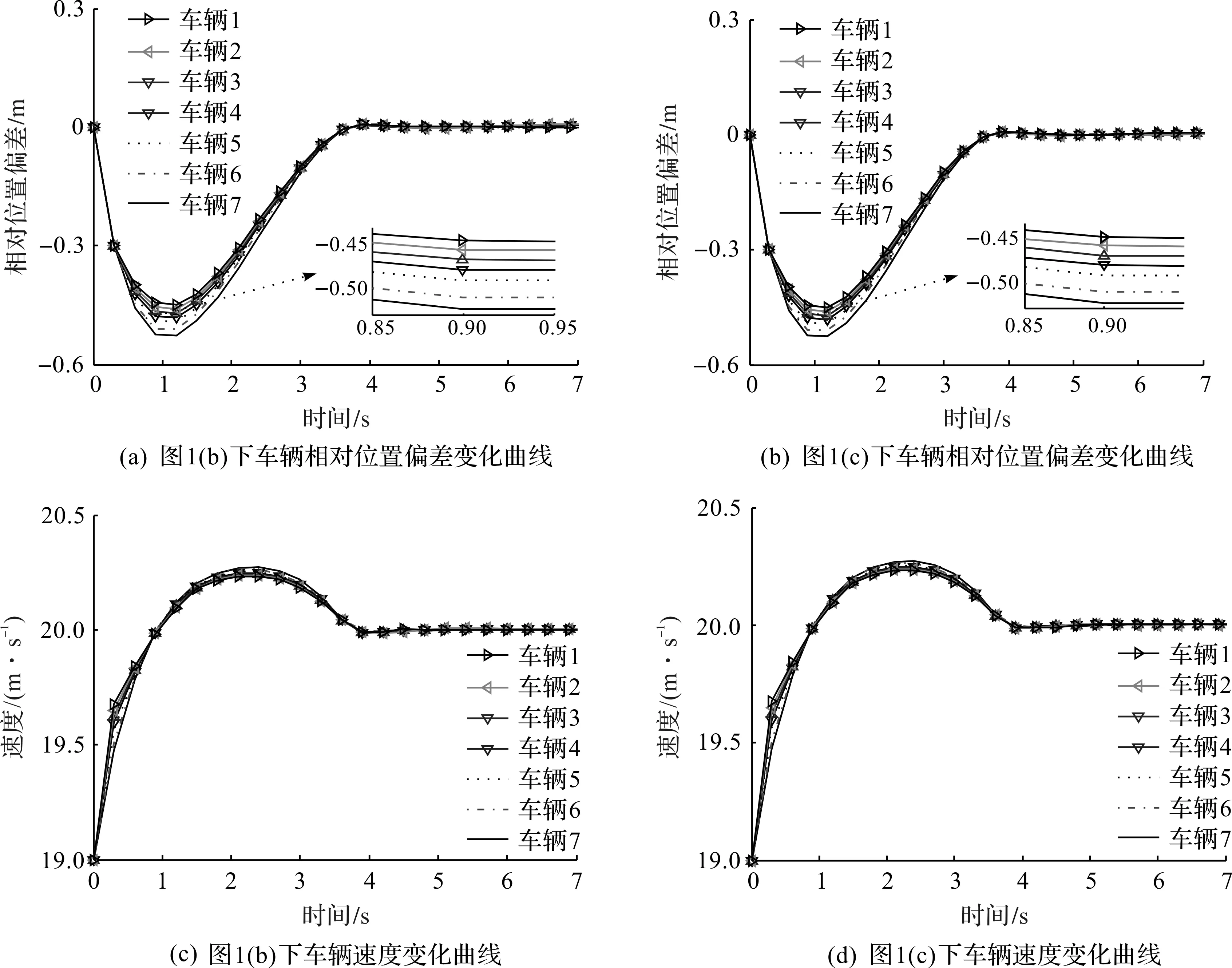
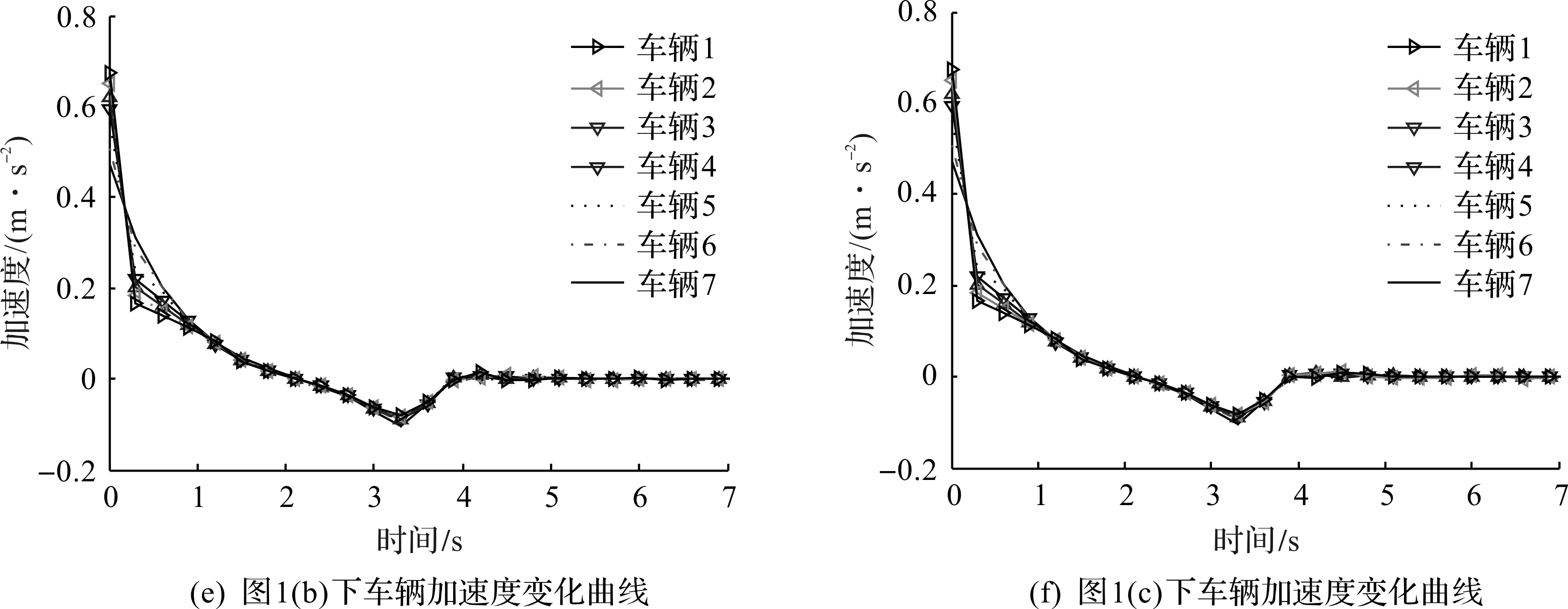
圖3 每輛車狀態曲線Fig.3 State curves of each vehicle

由圖2,3可知:在3種混合通信拓撲下車隊系統滿足跟蹤穩定,各輛車具有相同的速度,相對位置偏差最終收斂于0,實現狀態一致性,并收斂于穩態,且在行駛過程中滿足弦穩定,車輛間滿足安全間距,實現協同控制。同時加速度與車輛速度相對應,并在安全范圍內。

5 結 論

首先在任意通信拓撲下,針對具有狀態和控制約束的非線性車隊系統協同一致性穩態問題,提出了混合通信拓撲分布式雙層控制策略;然后通過構造收縮約束使跟蹤穩定性和動態一致性目標相關聯,并應用MPC三要素法和滾動時域建立了車隊系統穩定性和優化問題遞推可行性的充分條件;最后數值仿真驗證了所提策略可使車隊在任意通信方式下滿足跟蹤穩定性,車輛間保持安全間距,且狀態收斂于一致性穩態,車隊達到相應控制性能,實現協同控制。筆者研究為大型車隊系統的研究工作提供思路和參考,后續可進一步深入學習和研究。