阻水建筑物在河流數值模擬中的概化方法研究
王彩虹,程 雪,盧少為,由星瑩
(1. 湖北省水利水電規劃勘測設計院,湖北 武漢 430070; 2. 湖北省漢江興隆水利樞紐管理局,湖北 武漢 430062)
河道內的涉河建筑物(如橋梁、碼頭等)侵占部分河道過水面積,可能會對河道防洪造成一定影響。采用數學模型進行水流模擬時,采用的網格尺寸往往大于實際的橋墩尺寸,橋墩概化問題就顯得尤為重要[1]。
1 橋墩概化方法
合理的橋墩概化方法是準確模擬橋墩附近水流流態的關鍵條件。數值模擬中橋墩概化方法主要有兩種,等阻水面積法和等阻水體積法。
1)等阻水面積法[2]。當建筑物尺寸大于或與網格尺寸相當時,可直接根據建筑物高度來修改相應網格節點的河底高程;當建筑物尺寸相對網格尺寸較小時,假定河底高程增加值所阻擋的水流面積與工程所阻擋的水流面積相同,即迎流側阻水的投影面積相等,通過增加工程所在處網格節點的河底高程來反映工程的阻水影響。
2)等阻水體積法。等阻水體積法的思想是工程所在位置處的網格增加高程值所占用的有效容積與建筑物在水下所占用的有效體積相等。故當橋墩尺寸大于或與網格尺寸相當時,橋墩所在網格處的高程增加值為橋墩的水下高度;當橋墩尺寸小于網格尺寸時,橋墩所在網格處的高程增加值為橋墩的水下有效體積除以橋墩所在處的網格面積。通過橋墩所在處網格的地形數據修正來反映工程對水流的影響。
本文分別采用等阻水面積和等阻水體積的橋墩概化方法,運用二維模型進行數值計算,通過變化網格尺寸的大小,分別計算不同網格尺寸下的橋墩壅水值,探討等阻水面積和等阻水體積法的精度問題。
2 小尺度下橋墩水流模擬計算分析
2.1 小尺度下橋墩三維數值模擬計算方案
采用流體計算軟件FLUENT提供的RNGκ-ε湍流模型,結合水氣兩相流VOF模型[3]進行數值模擬,采用有限體積法對基本方程進行離散,運用PISO算法對壓力和速度進行耦合計算。
計算水槽長7.0 m,寬1.2 m,高0.3 m,橋墩尺寸為0.2 m×0.2 m×0.3 m。進口采用三種流量條件,分別為144、216、288 m3/h,出口水位始終固定在0.15 m。具體方案布置見表1。模擬計算結果分析見圖1、圖2。
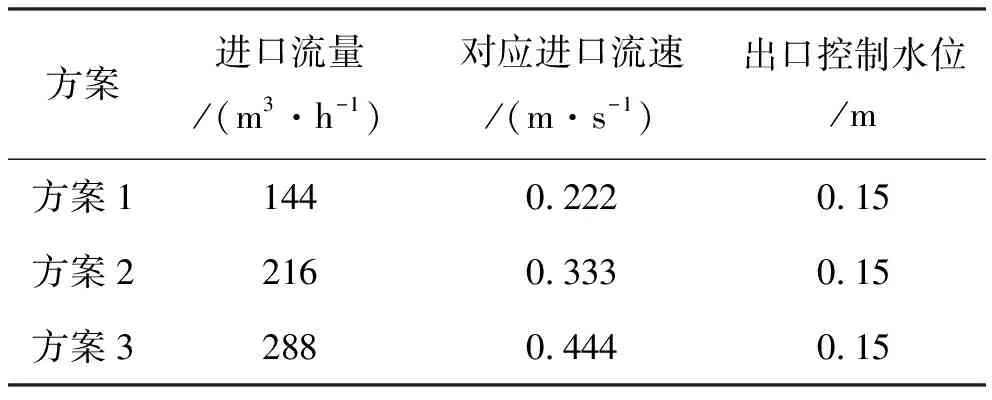
表1 三維數值模擬計算方案布置表
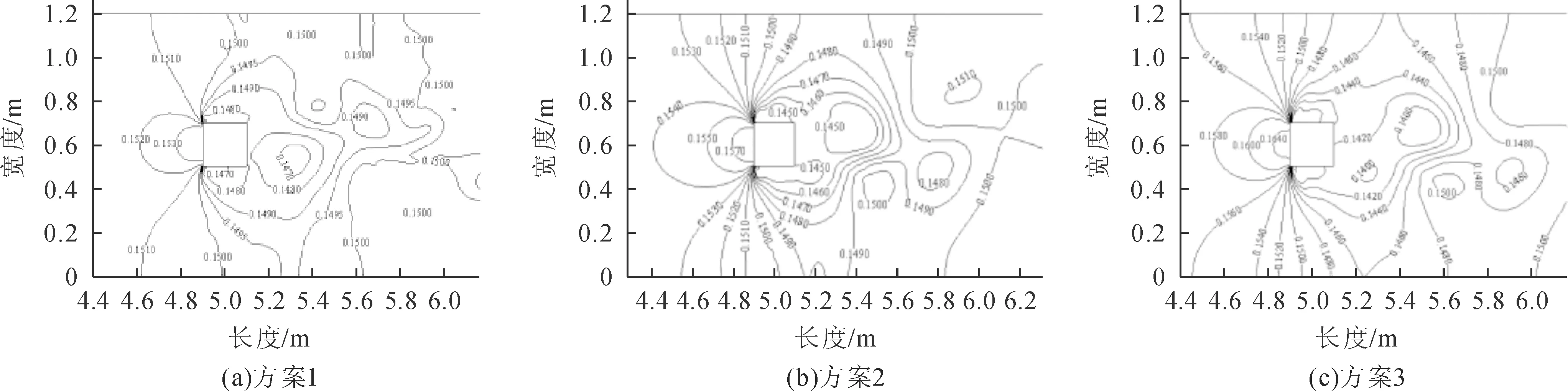
圖1 水位等值線圖

圖2 流速分布圖(1/3 h)
三種計算方案條件下,橋墩上游均出現壅水,而下游和橋墩兩側水位均降低;同時由于橋墩位于水槽橫向中心位置,橋墩迎水面及橋墩兩側水位呈對稱分布,橋墩背水側由于尾渦的形成和尾渦的不穩定性,水位的變化呈現整體降低,而局部散亂的分布。同時,由不同計算方案下的水位等值線圖可以看出,隨著流量的增加,橋墩前的壅水值呈增加趨勢。三種工況下,橋墩兩側流速均增加,而橋墩上游和下游流速均呈減小趨勢;同時由于橋墩位于水槽橫向中心位置,橋墩迎水面及橋墩兩側流速呈對稱分布,橋墩背水側由于尾渦的存在,流速存在負值,即橋墩背水側存在回流。同時可以看出,隨著流量的增加,流速變化值呈增加趨勢。從水位變化、流速變化可以看出,三維計算結果是合理的。
2.2 小尺度下橋墩二維數學模型計算
二維數學模型計算采用一般曲線坐標變換方法,控制方程及離散方程見文獻[4]。網格取為與橋墩大小一致的尺寸,故無論采用等體積法或等阻水面積法的概化方法,橋墩修建后的地形修正高度是一致的,均為自由水面下的橋墩高度。糙率取為0.032 3。計算條件取為與三維模型一致,見表1。
本文主要討論的是橋墩前后的壅水跌水問題,故主要從自由表面的水位來分析。三維和二維的計算結果如圖3所示。
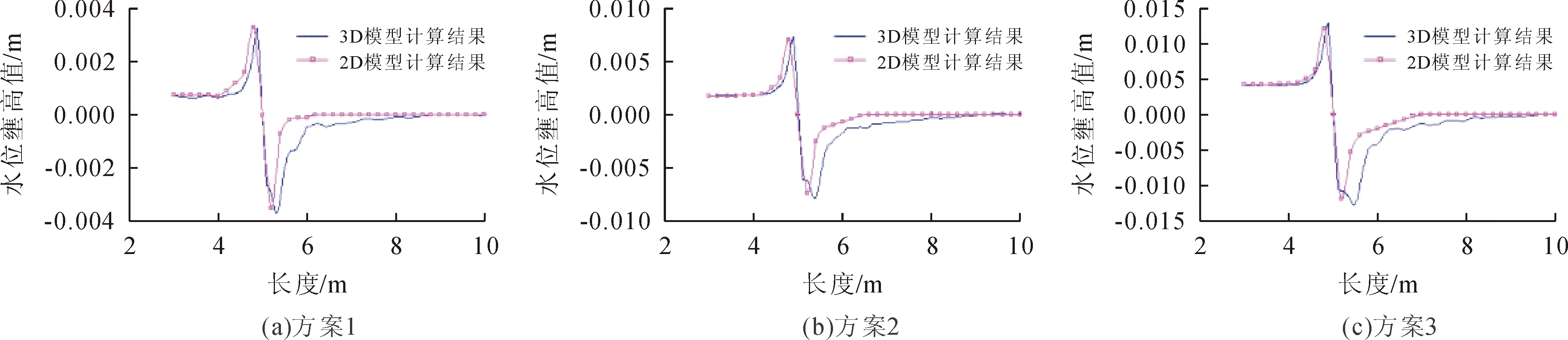
圖3 工程前后水位變化圖
從橋墩附近的壅水情況可以看出,各種工況下,二維模型模擬出的橋墩上下游的水位變化情況與三維模型模擬出的結果基本上一致。在跌水范圍上,二維模型的模擬結果比三維模型的結果稍微偏小。但總的來說,二維模型的計算結果與三維數模的計算結果擬合較好,且放映了橋墩上游壅水,下游跌水并沿程恢復的一般水力學特性,說明該模型在模擬橋墩附近的水位變化情況的精度是較高的。
3 天然河道橋墩二維數值模擬計算分析
3.1 計算網格的布置
將一條長為6 000 m,寬為600 m的河道作為研究對象,底坡為0.000 1,橋墩長10 m×寬10 m×高20 m。網格的大小分別為10 m×10 m、20 m×20 m、30 m×30 m、40 m×40 m、50 m×50 m。
3.2 計算方案的確定
進口流量控制為8 000 m3/s和6 000 m3/s,出口水位控制在10 m,由于河道出口位置的地形高程為0,故出口水深即為出口水位。為了使計算結果能夠明顯的反映規律,糙率取值比一般河道稍大一些,取值為0.032 3。由網格布置方案和橋墩尺寸,分別運用等阻水面積和等阻水體積法修正地形,可得到不同網格大小情況下的地形修正值。具體計算工況和計算方案如表2和表3所示。

表2 計算工況布置表
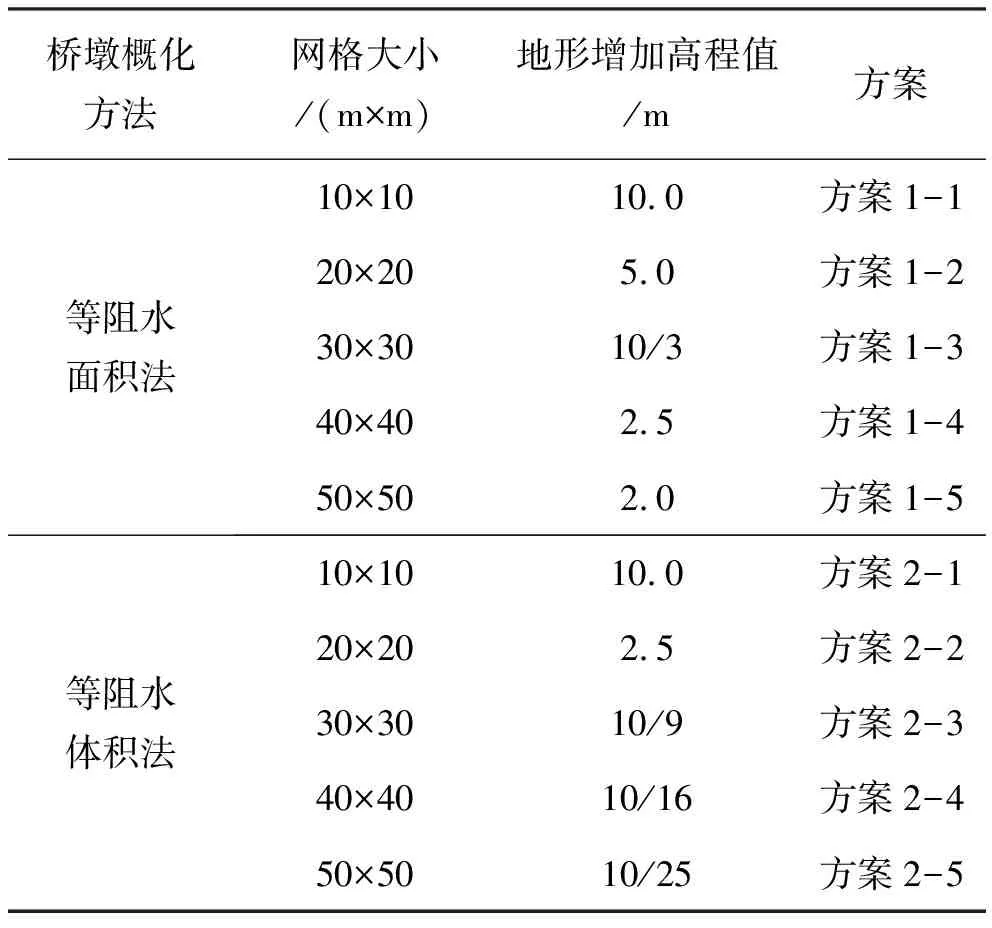
表3 計算方案布置表
3.3 不同橋墩概化方法下橋墩壅水結果分析
3.3.1 等阻水面積法的橋墩壅水結果分析
采用等阻水面積的橋墩概化方法,工況1條件下不同網格大小的計算結果見圖4,工況2條件下不同網格大小的計算結果見圖5,表4統計了采用等阻水面積法,工況1和工況2條件下不同網格尺寸下的最大壅水值。
通過圖4、圖5及表4可以看出,運用等阻水面積的橋墩概化方法,同種工況下,采用不同的網格尺寸計算出的橋墩最大壅水值不一致,且計算出的橋墩最大壅水值隨著網格尺寸的增加而逐漸減小。采用相同的橋墩概化方法,不同工況下,相同網格尺寸計算出的橋墩最大雍水值不同,且計算出的橋墩最大壅水值隨著流量的增加而逐漸增加。
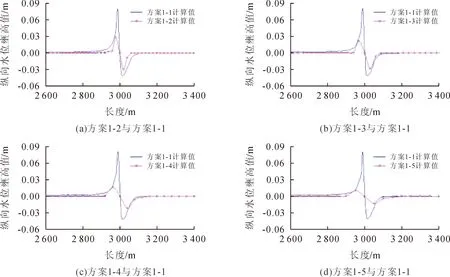
圖4 方案1-2、1-3、1-4、1-5與1-1水位壅高值對比圖(等阻水面積法,工況1)
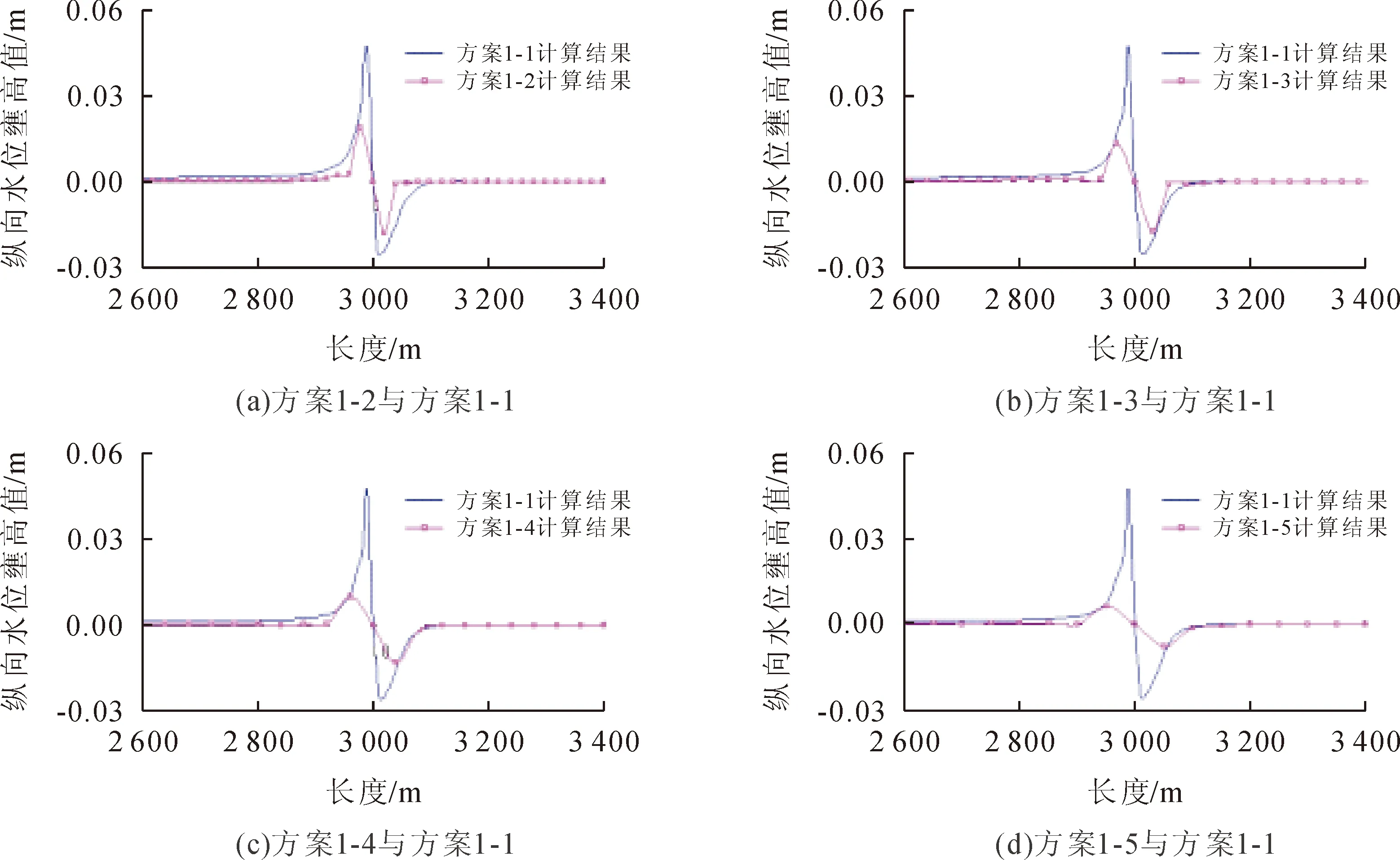
圖5 方案1-2、1-3、1-4、1-5與1-1縱向水位壅高值對比圖(等阻水面積法,工況2)
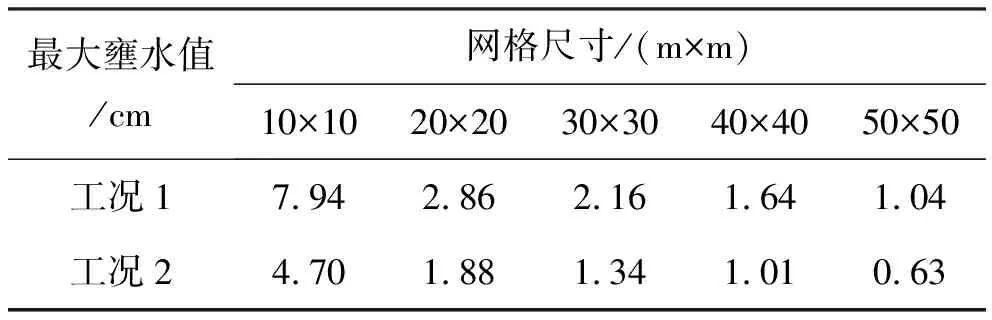
表4 不同網格尺寸下的橋墩最大壅水值(等阻水面積法)
3.3.2 等阻水體積法的橋墩壅水結果分析及修正
采用等阻水體積的橋墩概化方法,工況1條件下不同網格大小的計算結果見圖6,工況2條件下不同網格大小的計算結果見圖7,表5統計了采用等阻水體積法,工況1和工況2條件下不同網格尺寸下的最大壅水值。
通過圖6、圖7及表5可以看出,運用等阻水體積的橋墩概化方法,同種工況下,采用不同的網格尺寸模擬計算出的橋墩最大壅水值不一致,且計算出的橋墩最大壅水值隨著網格尺寸的增加而逐漸減小。采用相同的橋墩概化方法,不同工況下,相同網格尺寸計算出的橋墩最大雍水值不同,且計算出的橋墩最大壅水值隨著流量的增加而逐漸增加。
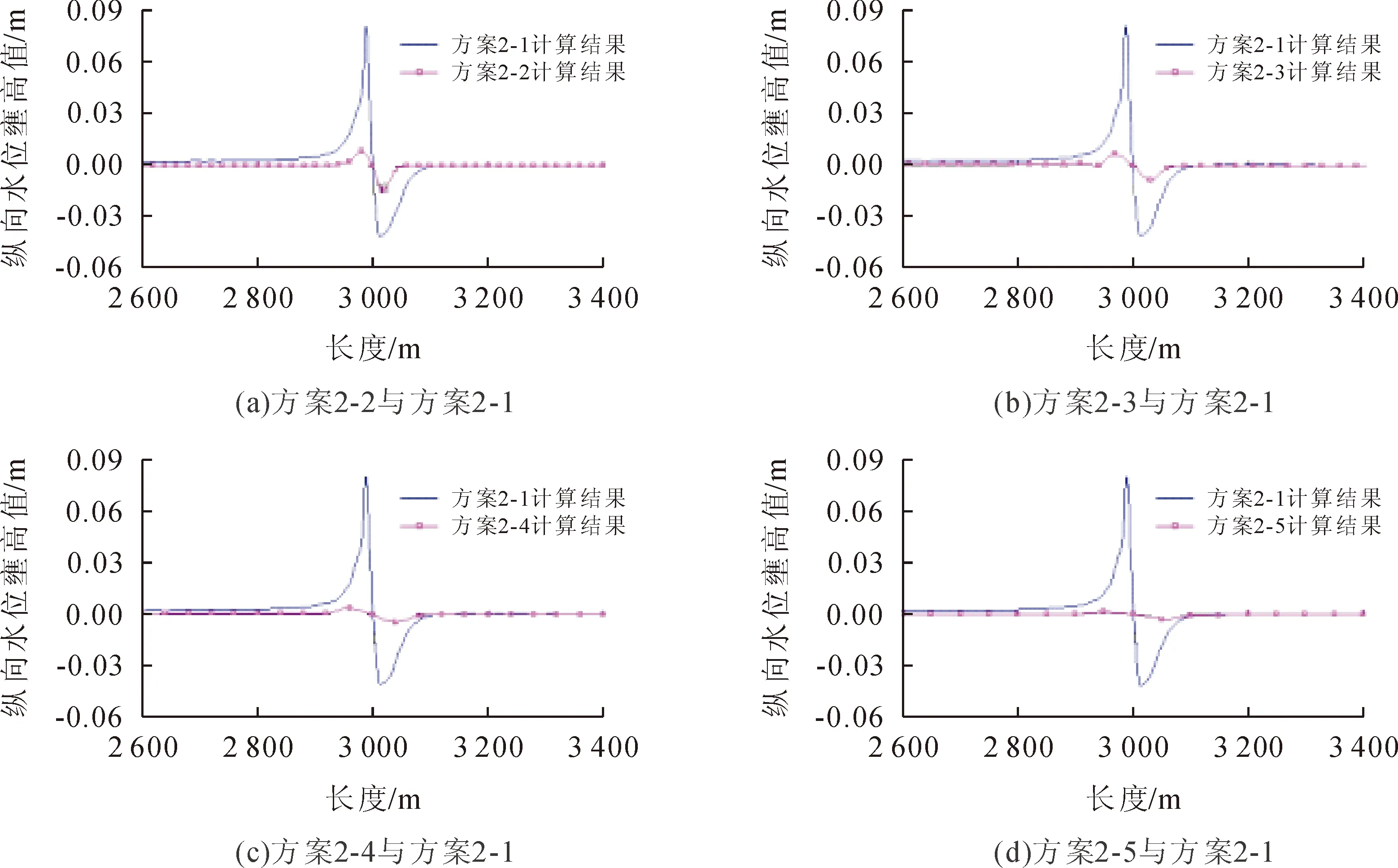
圖6 方案2-2、2-3、2-4、2-5與2-1水位壅高值對比圖(等阻水體積法,工況1)
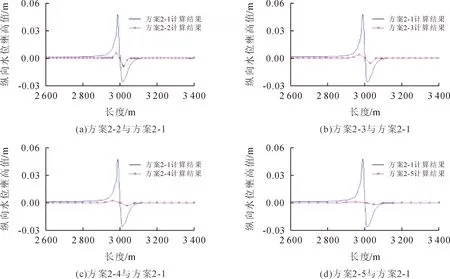
圖7 方案2-2、2-3、2-4、2-5與2-1水位壅高值對比圖(等阻水體積法,工況2)
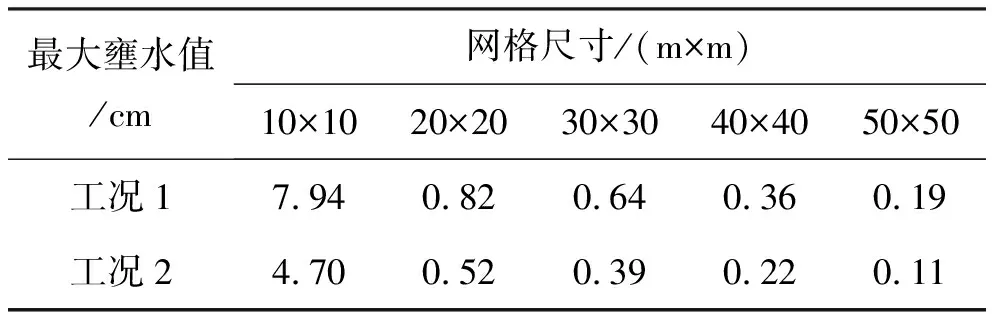
表5 不同網格尺寸下的橋墩最大壅水值(等阻水體積法)
4 結 語
1)運用相同橋墩概化方法,同種工況下,不同網格尺寸計算出的橋墩最大雍水值不同,且隨著網格尺寸的增加而逐漸減小。不同工況下,相同網格尺寸計算出的橋墩最大雍水值不同,且計算出的橋墩最大壅水值隨著流量的增加而逐漸增加。
2)運用不同橋墩概化方法,同種工況下,相同較大網格尺寸下計算出的橋墩最大壅水值不一致,等阻水面積法較等阻水體積法計算結果更接近準確值。
3)運用不同橋墩概化方法,大網格尺寸下兩種概化方案得到的壅水值均較小,而小網格(網格大小與橋墩尺寸一致或小于橋墩尺寸)的壅水結果是比較準確的,可以以此作為標準,引進修正系數對大網格的概化方法進行修正。

