基于LSTM和IGA-BP的酒精度預測模型
張建華 商建偉 王 唱 趙 巖 李克祥 李祥利
(河北工業大學機械工程學院,天津 300401)
白酒是中國特有的傳統酒種之一,仍保留著傳統手工釀造工藝,摘酒是蒸餾過程中一道極為重要的工序[1-2]。分段摘酒是按照不同的酒精度區間將流酒過程中原酒劃分為不同的階段,進行分段存儲。釀酒行業常用的摘酒方式為看花摘酒,摘酒工人通過流酒過程酒花的變化判斷當前酒精度值,進行分段摘酒,完全依賴摘酒工的個人經驗。
目前常用的酒精度檢測方法有密度計法[3-4]、分析儀器法[5-8]和傳感器法[9]等。Lachenmeier等[3]利用振蕩式密度計法實現白酒酒精度檢測,對低濃度酒檢測精度較高。酒精度分析儀器包括近紅外光譜儀[5]、氣相色譜儀[6]、核磁共振氫譜儀[7]、拉曼光譜儀[8]等。Santos等[9]還設計了基于電磁傳輸線作為在線檢測酒精含量的傳感器,通過測量傳輸線內傳播的TEM模式的電磁衰減來檢測溶液中的酒精含量。此外,還有基于圖像處理算法[10]實現自動摘酒的方法。上述研究工作對于酒精度的檢測具有靈敏度高,結果準確等優點,但存在檢測時間較長和受環境影響等問題,不適用于酒廠實際流酒過程檢測。
研究擬通過檢測音叉在不同模態不同濃度酒精溶液下的頻率值,判斷溶液酒精度值。采用LMS濾波算法和LSTM神經網絡提高音叉檢測頻率穩定性和實現音叉頻率動態補償,基于改進遺傳算法優化BP神經網絡建立酒精度預測模型,以期為分段摘酒過程酒精度檢測提供一種快速精準檢測方法。
1 基于酒精度建模的分段摘酒系統
分段摘酒是通過采集流酒過程音叉頻率值、音叉內置溫度值和流酒溫度值,通過PLC相關組件和酒精度計算模型實現酒精度在線計算,將酒精度數與控制系統預設酒精度數進行對比判斷,控制各階段電磁閥動作,使原酒流向不同的儲存桶,分段摘酒系統流程示意圖如圖1所示。
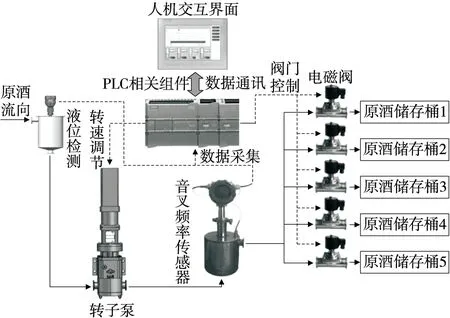
圖1 分段摘酒系統流程示意圖Figure 1 Process diagram of segmented wine picking system
2 多模態數據采集與自適應濾波
2.1 材料與儀器
2.1.1 材料與試劑
乙醇:分析純,江蘇強盛功能化學股份有限公司;
蒸餾水:江蘇沭陽科泓商貿有限公司。
2.1.2 儀器設備
音叉頻率傳感器:GJM-801型,西安市高精密儀器廠;
恒溫水浴槽:YTSC-15A型,上海葉拓儀器儀表有限公司;
溫度傳感器:PT100型,北京賽億凌科技有限公司;
電子天平:AUY120型,島津企業管理(中國)有限公司;
轉子泵:PSA2型,北京帕普生泵業有限公司。
2.2 音叉頻率傳感器改進
音叉頻率傳感器內置溫度傳感器安裝在機械支體內部,存在對液體溫度響應不及時問題,為解決此問題,添加額外的液體溫度傳感器,用于測量溶液溫度。將音叉頻率傳感器與液體溫度傳感器進行集成,通過RS485進行數據輸出。為緩解音叉傳感器存在的邊界效應問題[11],提高檢測精度,音叉頻率傳感器安裝管徑設計為DN160。
2.3 靜態試驗數據采集
利用島津電子天平、恒溫水浴槽、無水乙醇和蒸餾水配置20 ℃下不同濃度的酒精溶液。通過島津電子天平測量溶液密度,利用PT100溫度傳感器檢測溶液溫度,查詢《新編酒精密度濃度和溫度常用數據表》[12],根據所測密度和溫度得到所配溶液標準酒精度值,并進行標記。按照實際流酒過程酒精度分布區間,配置40%~80%vol的30個不同酒精度的酒精溶液樣本,其中40%~60%vol,每個溶液樣本遞增2%vol,60%~80%vol,每個溶液樣本遞增1%vol。
將30個酒精溶液樣本分別放入音叉頻率傳感器檢測容器,在水浴槽進行不同溫度區間恒溫加熱,記錄每個酒精溶液樣本在室溫至40 ℃不同溫度區間下的音叉頻率值、音叉內置溫度值和溶液溫度值,每個溫度區間遞增1.5 ℃。待附加液體溫度傳感器數值穩定時,利用Matlab記錄此試驗條件下的數據,部分數據記錄見表1。
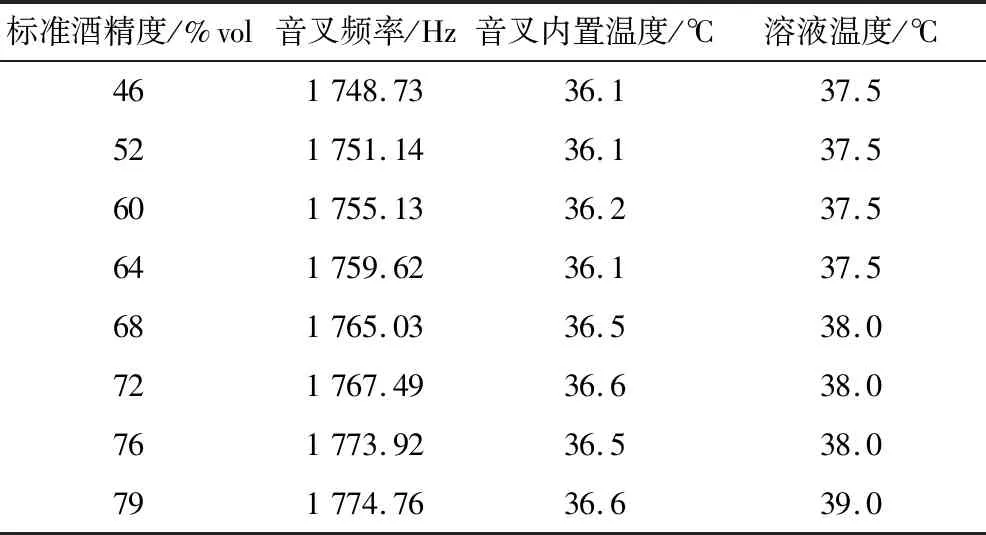
表1 部分數據記錄表Table 1 Partial data record sheet
2.4 動態試驗數據采集
流酒過程不同時刻流酒速度和酒精度不同,對音叉頻率值產生影響,導致音叉在不同模態下的相同濃度酒精溶液會有不同的振動頻率。利用分段摘酒設備和酒精溶液樣本采集動態試驗條件下音叉在不同泵轉速不同濃度酒精溶液下的頻率值,音叉頻率方差如圖2所示,當泵轉速較高時,音叉頻率方差較大,音叉頻率不穩定,泵轉速較低時,音叉頻率方差較小,音叉頻率較穩定。
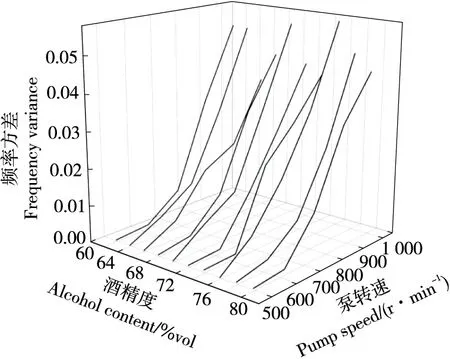
圖2 泵轉速—音叉頻率方差圖Figure 2 Variogram of pump speed-tuning fork frequency
2.5 數據處理流程
靜態試驗條件下不存在泵轉速對音叉檢測頻率的影響,音叉檢測頻率穩定,且利用恒溫水浴槽更容易測得恒溫下音叉在不同濃度酒精溶液下的振動頻率。因此將靜態試驗條件下數據作為酒精度標定數據,把靜態試驗條件下音叉在不同溫度和濃度酒精溶液下的音叉頻率值作為音叉在動態試驗條件下的音叉頻率補償值。將動態試驗條件音叉在不同濃度酒精溶液不同泵轉速下的音叉頻率平均值作為LMS自適應濾波音叉期望頻率值。
研究采集不同模態、不同濃度酒精溶液下音叉動態頻率值fd、音叉內置溫度t1、溶液溫度t2和動態試驗條件下泵轉速n。將音叉動態頻率fd作為LMS自適應濾波的輸入,輸出為濾波后頻率fl。將音叉動態頻率fd、泵轉速n、音叉內置溫度t1和溶液溫度t2作為LMS期望信號調整模型輸入,輸出為音叉在不同濃度不同轉速下的音叉期望頻率fq。將濾波后音叉頻率fl、音叉內置溫度t1、溶液溫度t2和泵轉速n作為LSTM音叉頻率動態補償模型的輸入,輸出為音叉頻率補償值fb。將音叉頻率補償值fb、音叉內置溫度t1和溶液溫度t2作為IGA-BP酒精度擬合模型的輸入,輸出為酒精度q,實現動態流酒過程酒精度在線計算,數據處理流程如圖3所示。
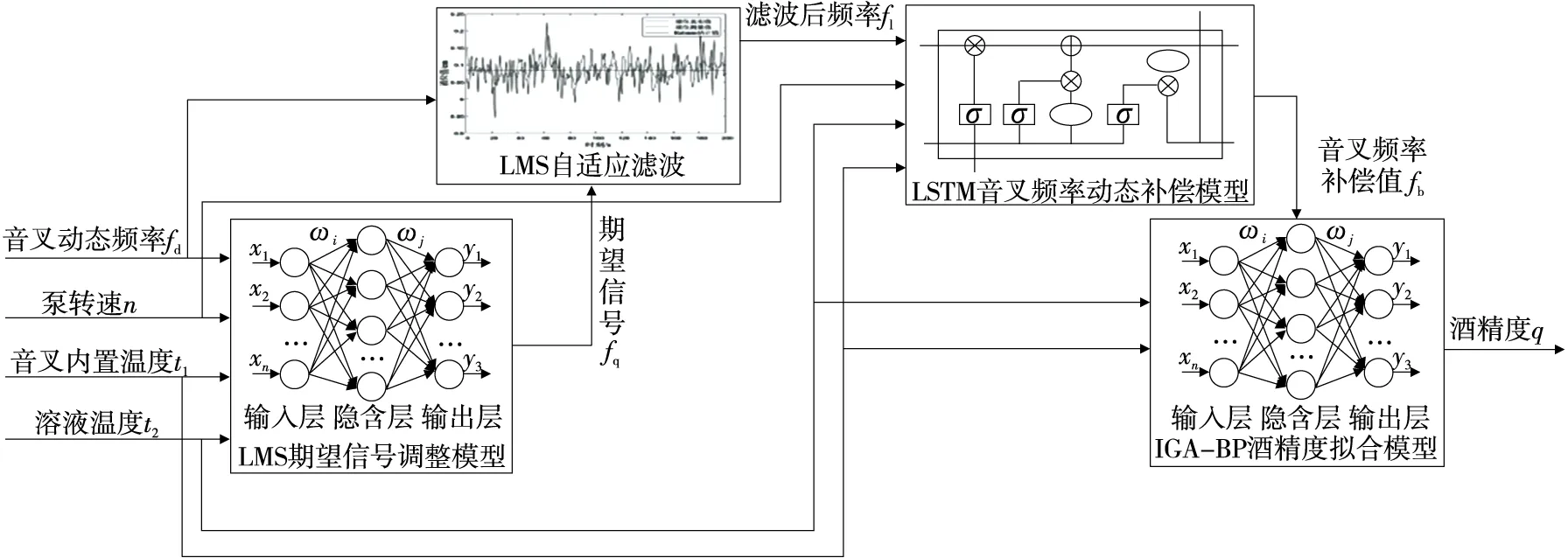
圖3 數據處理流程圖Figure 3 Data processing flow chart
2.6 音叉動態頻率自適應濾波
為提高動態流酒過程音叉頻率穩定性,基于最小均方(Least Mean Square,LMS)算法實現音叉動態頻率自適應濾波。LMS濾波算法基于維納濾波算法,采用隨機梯度下降的方法實現代價函數最小化,具有計算復雜度低、無需統計數據的先驗知識和均值無偏地收斂到維納解等優點,在信號濾波方面得到廣泛應用。LMS自適應濾波器的結構如圖4所示,包括橫向濾波器和LMS算法兩部分。
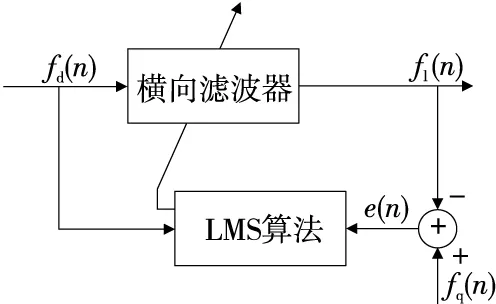
圖4 LMS自適應濾波器框圖Figure 4 Block diagram of LMS adaptive filter
橫向濾波器本質是FIR結構的維納濾波器,LMS算法根據期望信號fq(n)與輸出信號fl(n)的誤差e(n)調整橫向濾波器的權系數向量,適應隨機信號的時變統計特性[13]。基于BP神經網絡建立LMS自適應濾波期望信號調整模型,設定神經網絡隱含層神經元個數為6個,設定最大訓練次數為1 000,學習速率為0.1,目標誤差精度為0.001。濾波結果如圖5所示,音叉檢測頻率方差由0.022 54降為0.002 17。
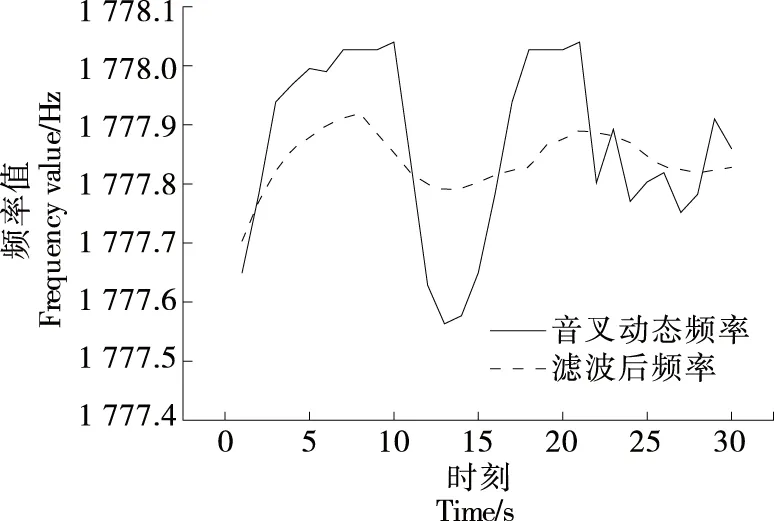
圖5 音叉頻率自適應濾波結果Figure 5 Tuning fork frequency adaptive filtering results
3 酒精度預測模型及結果分析
3.1 基于LSTM的音叉頻率動態補償模型
流酒過程音叉頻率補償值受歷史時刻工況的影響,對于音叉頻率補償值預測問題,傳統神經網絡的輸出是由當前時刻的輸入決定,而忽視了歷史時刻的影響。循環神經網絡(recurrent neural network,RNN)是在隱藏層神經元上添加指向自己的反饋回路,使得上一時刻隱藏層狀態也作為下一時刻的輸入,從而將歷史信息考慮在內,達到短期記憶的目的[14]。LSTM網絡是一種特殊的RNN,它包含一個或多個記憶單元(cell)以及遺忘門(forget gate)、輸入門(input gate)和輸出門(output gate) 3個控制門,LSTM神經元使其能夠存儲并傳遞長期記憶和短期記憶,克服了傳統RNN的長期依賴問題。
LSTM神經網絡由時序數據輸入層、隱含層和輸出層組成,常用的序列預測法主要有單步法和多步法[15]。單步法是以固定時間步的歷史數據預測下一時刻的值,每次預測網絡的輸入均為已知實際觀測值,預測精度高,利于觀測短期內性能的波動。多步法是指以固定時間步的歷史序列預測未來多個時間步的序列值。實際流酒過程中,音叉頻率補償值受歷史網絡補償值的影響,為提高預測精度,采用單步預測法。單步預測以不同濃度酒精溶液在動態試驗條件下固定10個時間步的泵轉速、濾波后音叉動態頻率、音叉內置溫度、溶液溫度作為LSTM網絡單步預測的輸入,將試驗酒度在此溫度下的靜態試驗音叉頻率值作為LSTM網絡下一時刻的預測輸出。設置LSTM網絡隱含單元數目為200,訓練次數為2 000次。濾波后音叉頻率和音叉頻率補償值時序數據圖如圖6所示。
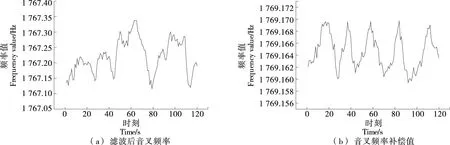
圖6 樣本數據時序圖Figure 6 Sample data timing diagram
3.2 音叉頻率補償結果及對比分析
LSTM神經網絡音叉頻率動態補償模型和BP神經網絡音叉頻率動態補償模型預測輸出如圖7所示。由圖7可以得出,LSTM神經網絡預測值與期望值的最大誤差為0.004 5,最小誤差為0,平均預測誤差為0.001 3;BP神經網絡預測值與期望值最大誤差為0.008 4,最小誤差為0.000 4,平均預測誤差為0.002 8。對比發現LSTM網絡對音叉頻率補償值預測精度較高且更符合實際頻率變化規律。
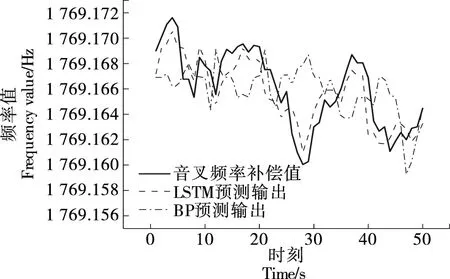
圖7 音叉頻率補償值預測結果Figure 7 Tuning fork frequency compensation value prediction results
3.3 基于IGA-BP神經網絡的酒精度預測模型
經LMS自適應濾波和LSTM神經網絡音叉頻率動態補償模型解決了因泵運動導致的音叉頻率檢測不穩定及頻率補償問題。實際流酒過程音叉頻率、音叉內置溫度、溶液溫度和標準酒精度之間的計算是一種非線性、時變性多因素復雜系統的數據預測問題,神經網絡在數據預測領域得到廣泛應用。
BP神經網絡具有良好的非線性數據預測能力,但存在收斂速度慢、易陷入局部最優等缺陷,無法得到全局最優解。引入具有良好全局搜索能力的遺傳算法(Genetic Algorithms,GA),并對傳統遺傳算法中交叉和變異概率進行改進,得到改進遺傳算法(Improved Genetic Algorithms,IGA),尋優得到BP神經網絡的最佳權值和閾值,提高BP神經網絡的收斂速度,減少BP神經網絡陷入局部最優的可能。
在傳統的遺傳算法中,交叉概率和變異概率為常數,但在實際遺傳算法的進化過程中,進化前期和后期所需要的交叉和變異程度不同。在遺傳算法的前期,因為個體的適應度較差,需要較大的交叉概率值擴大算法的全局搜索范圍,較小的變異概率來保存個體優良基因;而在后期,個體的適應度高于平均的適應度值,需要較小的交叉概率來降低全局搜索能力,較大的變異概率來增強局部搜索能力,改進后的交叉概率Pc和變異概率Pm公式[16]如下:
(1)
(2)
式中:
Fmax——交叉的兩個個體的最大適應度;
Fmean——種群個體平均適應度值;
F——種群中父代染色體的適應度值;
m——遺傳算法當前的迭代次數;
mmax——最大迭代次數。
根據交叉和變異概率取值范圍,設初始值Pc,max為0.9,Pc,min為0.4,Pm,max為0.09,Pm,min為0.005。
利用不同試驗模態下數據采集結果,基于改進遺傳算法優化BP神經網絡建立以音叉頻率補償值fb、音叉內置溫度t1、酒精溶液溫度t2為輸入變量,標準酒精度數q為輸出變量的酒精度預測模型,標準酒精度q計算公式為:
(3)
式中:
x1——標準化后的音叉補償頻率,Hz;
x2——標準化后音叉內置溫度,℃;
x3——標準化后溶液溫度,℃;
n——隱含層神經元個數;
ωm,i——經改進遺傳算法優化后BP神經網絡輸入層與隱含層的連接權值;
ωj——經改進遺傳算法優化后BP神經網絡隱含層與輸出層的連接權值;
bi——隱含層的閾值;
B——輸出層的閾值。
經改進遺傳算法尋優得到的BP神經網絡最佳權值和閾值如表2所示,表2中ωm,i(m=1,2,3;i=1,2,…,8)分別表示3個輸入對隱含層的連接權值。
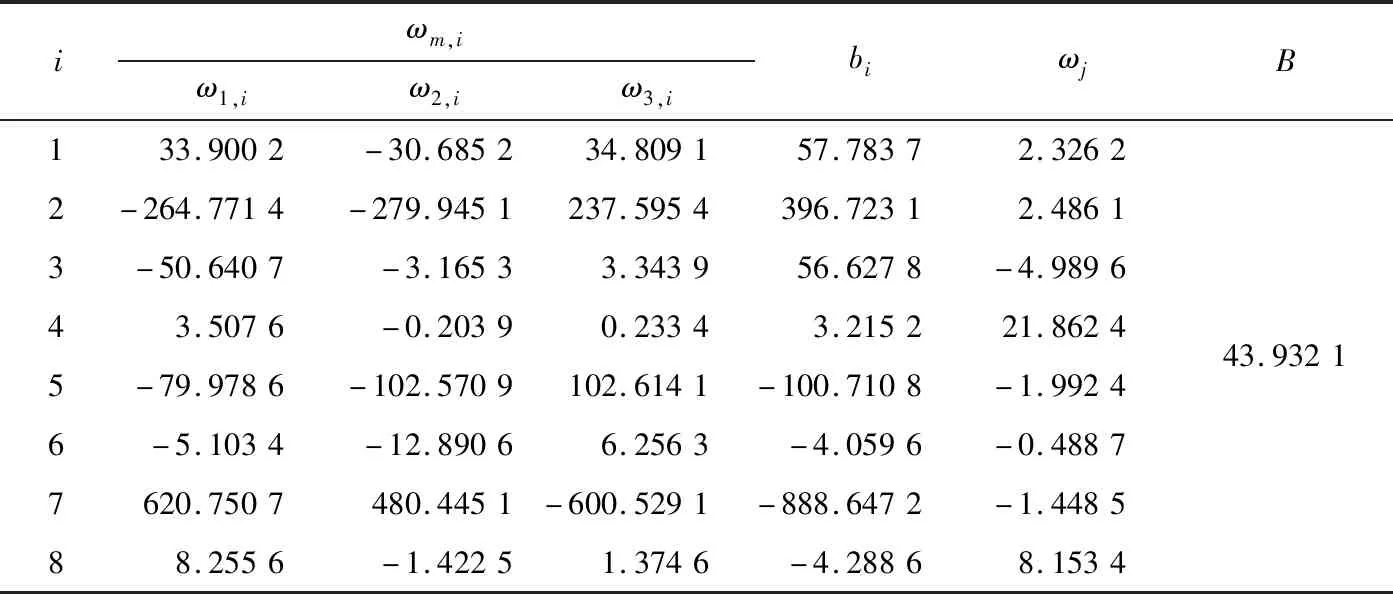
表2 BP神經網絡最佳權值和閾值Table 2 Optimal weights and thresholds of BP neural network
基于改進遺傳算法優化BP神經網絡建立酒精度預測模型,設置遺傳算法初始種群大小為30,迭代次數為60。BP神經網絡輸入為音叉頻率補償值、音叉內置溫度值和酒精溶液溫度值,輸出為標準酒精度值,隱含層神經元個數設置為8個,設定最大訓練次數為1 000,學習速率為0.1,目標誤差精度為0.000 1,酒精度預測模型結果如圖8所示。
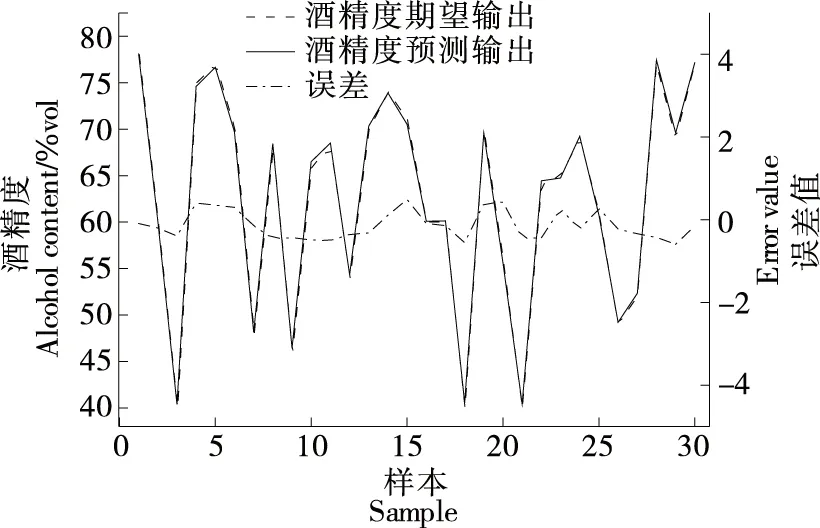
圖8 IGA-BP酒精度預測結果Figure 8 Prediction results of IGA-BP alcohol content
3.4 酒精度預測模型結果及對比
改進遺傳算法和傳統遺傳算法最佳個體適應度變化曲線如圖9所示。由圖9可以看出,改進后遺傳算法在進化24次時適應度曲線穩定,而傳統遺傳算法在進化50次時適應度曲線尚未穩定,說明改進后的遺傳算法能較快地搜索到合適的權值和閾值。
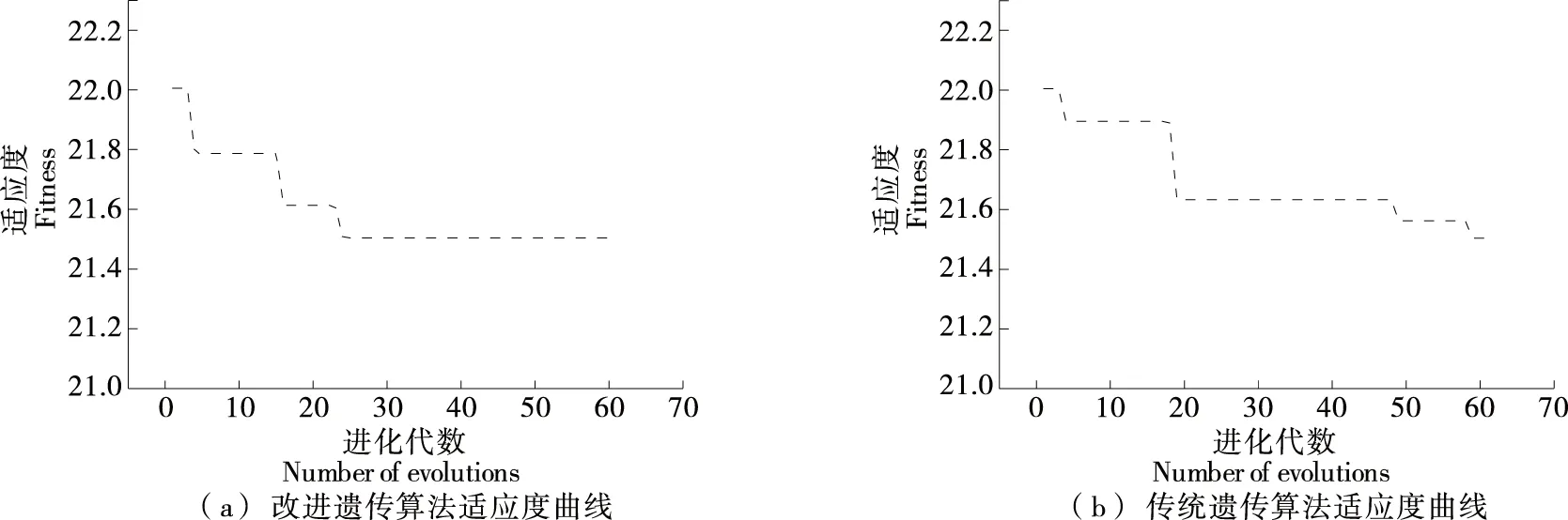
圖9 兩種遺傳算法適應度曲線Figure 9 Two genetic algorithm fitness curves
GA-BP神經網絡和IGA-BP神經網絡酒精度預測模型訓練結果曲線如圖10所示。由圖10可得,經遺傳算法優化BP神經網絡需30輪達到最優解,經改進遺傳算法優化BP神經網絡需11輪達到最優解。結果表明,改進遺傳算法能夠找到較優的權值和閾值,有效提高BP神經網絡收斂速度和減小網絡誤差。
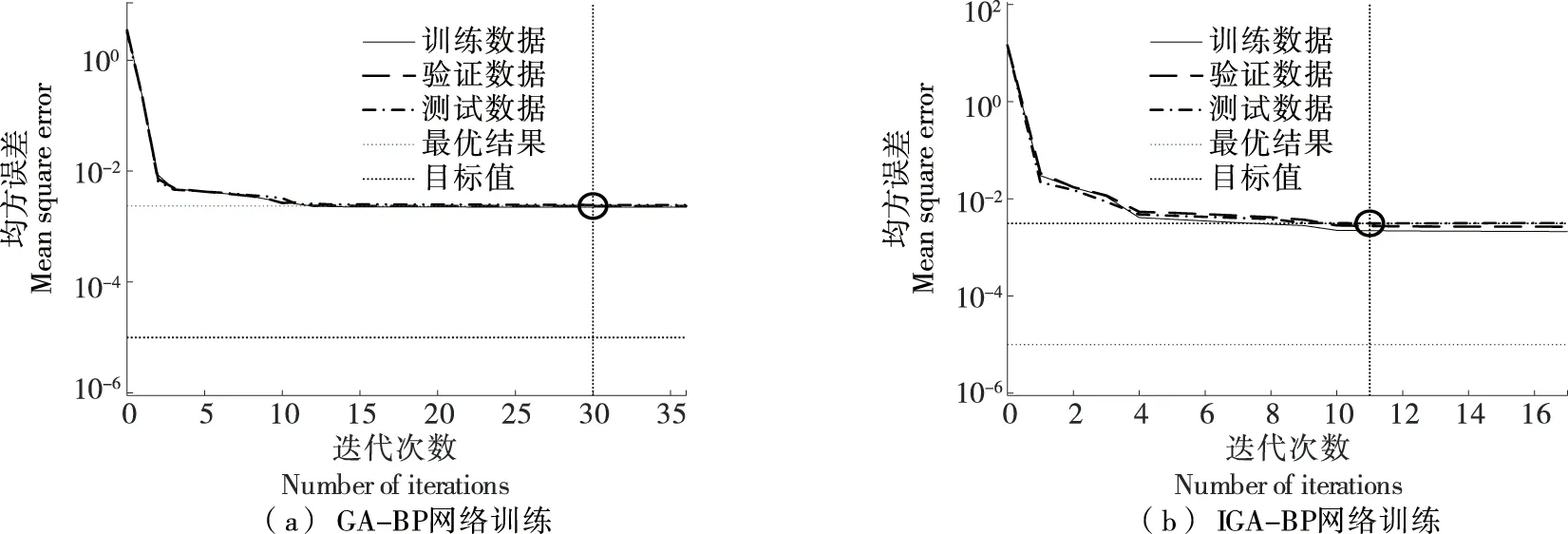
圖10 神經網絡訓練結果Figure 10 Neural network training results
為評價模型預測效果,引入均方根誤差和決定系數進行評價,均方根誤差越小,決定系數越大,預測結果越準確。BP神經網絡、GA-BP神經網絡和IGA-BP神經網絡標準酒精度預測模型結果對應的均方根誤差和決定系數如表3所示。由表3可得,IGA-BP神經網絡酒精度模型預測結果最準確。
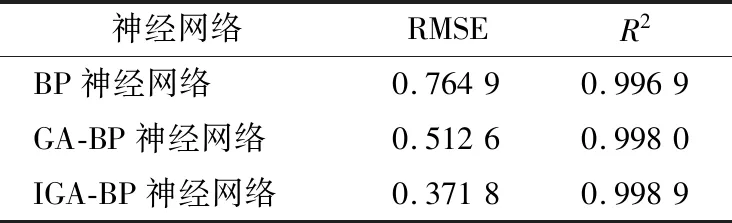
表3 酒精度預測模型對比Table 3 Comparison of alcohol prediction models
IGA-BP、GA-BP和BP神經網絡酒精度預測誤差結果如圖11所示。由圖11可以得出,IGA-BP神經網絡酒精度預測模型預測誤差最大值為0.61,平均預測誤差為0.381,GA-BP神經網絡酒精度預測模型預測誤差最大值為1.09,平均預測誤差為0.548,BP神經網絡酒精度預測模型預測誤差最大值為1.39,平均預測誤差為0.74。結果表明,IGA-BP神經網絡酒精度預測模型在預測精度上優于其他兩種酒精度預測模型。
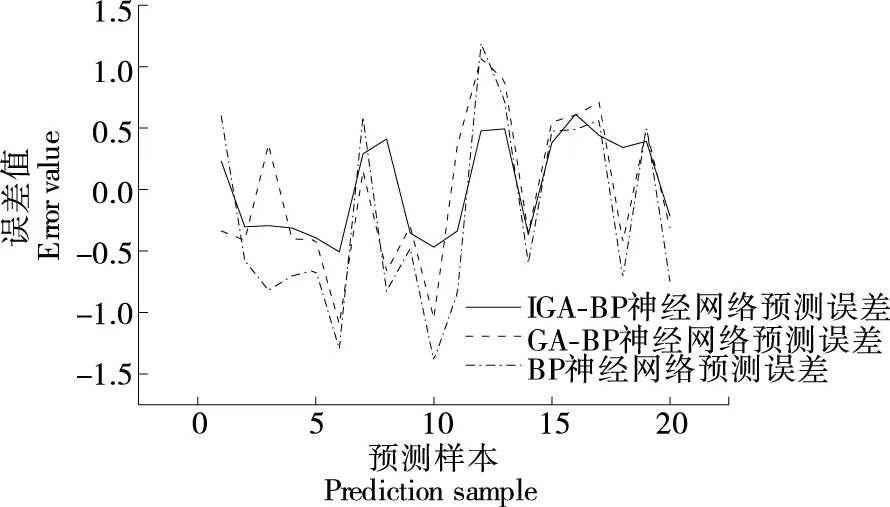
圖11 酒精度預測誤差Figure 11 Alcohol prediction error
4 結論
針對目前酒精度檢測方法存在的問題,提出了一種酒精度快速檢測的方法。采集音叉在不同模態、不同濃度酒精溶液下的試驗數據,采用LMS濾波算法提高了音叉檢測頻率穩定性,LSTM神經網絡音叉頻率動態補償模型平均預測誤差較傳統神經網絡預測結果提高了53.6%,基于改進遺傳算法優化BP神經網絡建立酒精度預測模型,模型在迭代次數和預測精度上優于傳統遺傳算法優化BP神經網絡和BP神經網絡建立的酒精度預測模型。酒精度檢測方法具有較高的精度和適用性,后續工作應深入研究動態環境下音叉檢測不穩定問題,提高酒精度檢測精度。

