抽水蓄能電站主廠房樓梯結構抗振性能研究

楊洪驍 伍鶴皋 傅 丹 劉曉勇

(1.武漢大學水資源與水電工程科學國家重點實驗室，武漢 430072;2.中國電建集團成都勘測設計研究院有限公司，成都 610072)

抽水蓄能電站主廠房中的板梁柱結構是容易被誘發(fā)強烈振動的部位，也一直是抗振設計關注的重點[1].過去相關研究主要聚焦在樓板結構型式上，武漢大學、大連理工大學和河海大學的研究人員分別結合不同的抽水蓄能電站開展了樓板結構抗振方面的研究[2-3].相比之下，樓梯結構的抗振一直未引起廠房土建方足夠的重視，幾乎沒有文獻報道樓梯結構的動力特性與抗振優(yōu)化設計.科研單位在開展廠房動力特性專題研究時也經常忽略或簡化樓梯這一復雜的結構[4].實際上，樓梯比樓板結構更加單薄，梯柱尺寸一般小于邊柱，且踏步厚度僅0.15～0.20 m.張河灣抽水蓄能電站的樓梯曾經出現(xiàn)劇烈振動，后來采取了增設立柱、鋼托梁及加大立柱截面尺寸等加固措施，振動才得以減弱[5].目前國內各設計單位對主廠房內樓梯結構有自己習慣的做法，設計主要以滿足正常的使用功能為目標，缺乏抗振設計的指導原則與優(yōu)化方法.為此，本文在詳細調研國內抽水蓄能電站樓梯設計資料的基礎上，總結出四類常用的樓梯結構型式，并建立精細化的有限元模型，開展樓梯結構動力特性研究，以期為抽水蓄能電站的抗振設計提供參考.

1 計算模型與方案

本文研究結合某抽水蓄能電站地下廠房開展，電站裝機容量2 400 MW，設8臺單機300 MW水泵水輪發(fā)電機組.發(fā)電機正常轉速為375 r/min，飛逸轉速為510 r/min.水輪機固定導葉和活動導葉數(shù)為22個，轉輪葉片數(shù)為9個.水輪機最大水頭為432.5 m，額定水頭400 m，最小水頭368.5 m.計算時在廠房上下游側混凝土與圍巖接觸的結點上施加彈簧單元，以模擬圍巖對廠房結構的彈性約束作用，機組段兩側考慮分縫按自由邊界處理.

在抽水蓄能電站主廠房中一般使用板式樓梯，本文收集了4種常用的板式樓梯結構型式，并建立了相應的有限元模型，如圖1～2所示.

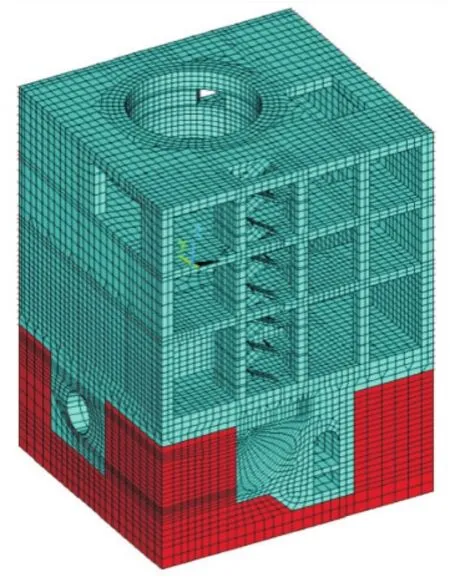
圖1 計算模型

方案1:樓梯間4根立柱尺寸為1.0 m×1.0 m，平臺板與立柱通過梁連接，梁尺寸0.5 m×0.25 m;

方案2:樓梯間上下游立柱之間設實體墻，平臺板與實體混凝土墻連接，墻體厚度0.3 m，其余部分與方案1相同;

方案3:在方案1的基礎上，在梯段與平臺連接處兩側各增加一根結構柱，結構柱尺寸為0.6 m×0.6 m，并用梁與平臺板連接，梁的尺寸為0.5 m×0.25 m;

方案4:在方案2的基礎上，于樓梯一側再增加實體混凝土墻，墻厚度為0.3 m，側墻與梯段及平臺之間為整體剛性連接.

2 踏步對樓梯結構動力特性的影響

在進行廠房結構有限元分析時，為簡化有限元模型和加快計算速度，通常不對樓梯踏步進行模擬，而實際上樓梯踏步對樓梯結構的剛度和質量均有影響.為此，本節(jié)對是否模擬樓梯踏步和考慮樓梯踏步質量進行對比分析.計算分為:模型1完整模擬樓梯踏步，如圖3(a)所示;模型2取消樓梯踏步結構，僅考慮樓梯板和其質量，如圖3(b)所示;模型3在模型2樓梯板上施加質量單元模擬踏步，質量單元數(shù)值大小等同于踏步質量，分布于樓梯板上，如圖3(c)所示.

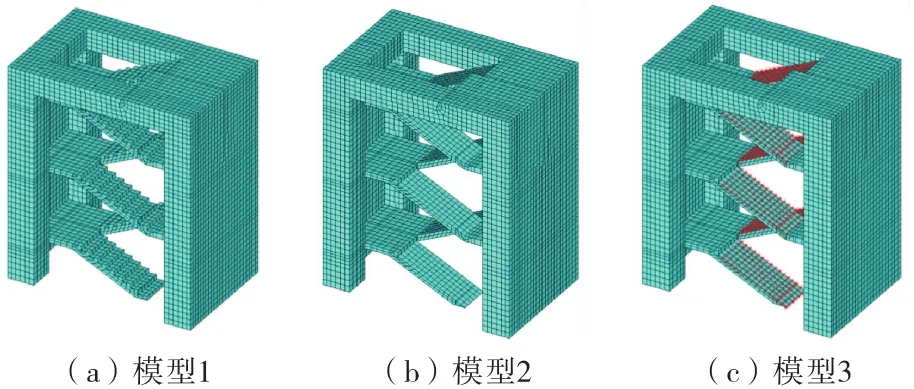
圖3 不同踏步模擬方式樓梯模型

根據計算結果，整理了3個模型樓梯結構的自振頻率，其基頻分別為29.9、31.1、28.2 Hz，其他頻率如圖4所示.

由圖中可以看出，與完整模擬樓梯踏步相比，模型2不按實際模擬樓梯踏步時，樓梯結構自振頻率整體升高，不模擬樓梯踏步雖然會降低樓梯結構整體剛度，但是樓梯踏步質量的減少明顯對樓梯結構自振頻率的影響更大，因而樓梯自振頻率升高;模型3使用質量單元模擬樓梯踏步時，樓梯結構自振頻率比模型1有所降低，因為模型中樓梯質量雖然保持一致，但是不考慮樓梯踏步降低了樓梯板與樓梯踏步形成的整體剛度.

在蝸殼范圍內施加轉輪葉片數(shù)頻率56.25Hz的脈動壓力，幅值為額定水頭的2%.圖5為3種踏步模擬方法樓梯結構的動位移云圖.

圖5 不同踏步模擬方式下樓梯振動位移(單位:m)

從圖中可以看出，3種模擬方式下樓梯結構動位移峰值均出現(xiàn)于母線層樓梯處，但模型2相比模型1動位移峰值提高了15.4%，模型3則比模型1動位移峰值降低了9.6%，說明完整模擬樓梯踏步最為精確，其次是模型3.綜合自振特性與動力響應計算結果來看，與按實際模擬的模型1相比，模型3建模更為簡便，模擬效果也比較好，可以作為廠房振動計算時樓梯的簡化模擬方式.

3 不同樓梯結構型式自振特性

根據上一節(jié)的研究結論，對樓梯結構進行動力分析時，對樓梯踏步完整模擬是有必要的，因此本節(jié)在考慮完整模擬樓梯踏步的前提下，借用"無質量地基"的概念，計算得到了圖2中4種方案樓梯結構的自振頻率，第一階振型如圖6所示，基頻分別為29.8、29.9、37.8、41.4 Hz，其他頻率如圖7所示.

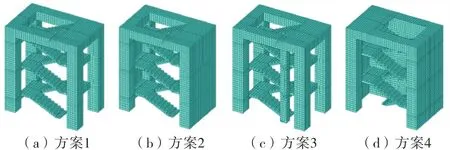
圖2 常用的4類樓梯結構型式

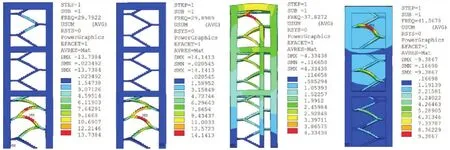
圖6 4種樓梯結構第1階振型圖

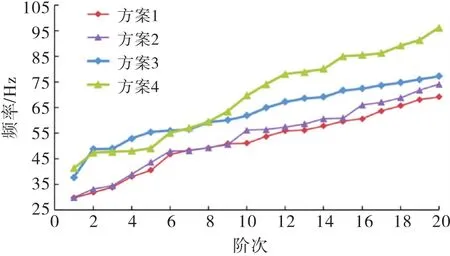
圖7 不同型式樓梯結構自振頻率

由圖7可以看出，方案1采用上下游平臺梁的樓梯結構自振頻率最低;方案2樓梯間兩端平臺與實體墻連接，各階自振頻率都有所提高，但幅值非常小，基頻僅提高0.33%，說明樓梯間兩端設置實體墻對自振頻率的提高效果非常有限;方案3在樓梯段與平臺連接處兩側各增加一根結構柱后，各階自振頻率比方案1均有明顯提高，其中基頻提高接近26.84%，說明中間立柱減小了樓梯段和平臺的跨度，對提高樓梯結構自振頻率效果顯著;方案4是在方案2的基礎上于樓梯間側面增加一面實體墻，其各階自振頻率與方案1相比同樣提高明顯，基頻提高約38.93%，尤其是高階頻率提高更大，說明方案3增加結構柱和方案4增加樓梯間側墻對提高樓梯結構的自振頻率效果最為明顯，上述兩種措施可以作為樓梯結構自振特性的有效調控措施.

4 不同樓梯結構型式動力響應

統(tǒng)計表明，已建和在建抽水蓄能電站地下廠房流道內轉輪葉片數(shù)頻率分布較為廣泛，轉輪葉片數(shù)頻率大多分布在30～75 Hz之間.因此本節(jié)通過掃頻的方法，在蝸殼流道內施加了30～75 Hz的中高頻脈動壓力，最大水頭的2%作為脈動壓力幅值，用以對比在不同頻率脈動壓力作用下4種方案樓梯的動力響應規(guī)律.分析各頻段樓梯結構的動位移分布，發(fā)現(xiàn)激振頻率34 Hz脈動壓力作用下，各方案均在母線層樓梯中間梯段豎向(Z向)動位移最大，如圖8所示.

圖8 34 Hz激振頻率作用下樓梯結構Z向動位移(單位:m)

比較4個方案樓梯間的動位移大小可見，方案1動位移最大，達0.186 mm，其次為方案2的0.151 mm，方案3和方案4分別為0.026 8 mm和0.027 3mm，相對方案1降幅在85.5%以上，減振效果明顯，而且激振頻率在30～75 Hz之間變化時均存在此規(guī)律，說明可以通過在樓梯間增加側墻的方式大幅減小樓梯結構的動力響應，無論激振頻率高低均可取得較好的抗振效果.

為了更詳細地了解4種樓梯結構型式的抗振性能，圖9整理了30～75 Hz頻率范圍內母線層樓梯特征點動位移隨激振頻率的變化規(guī)律.

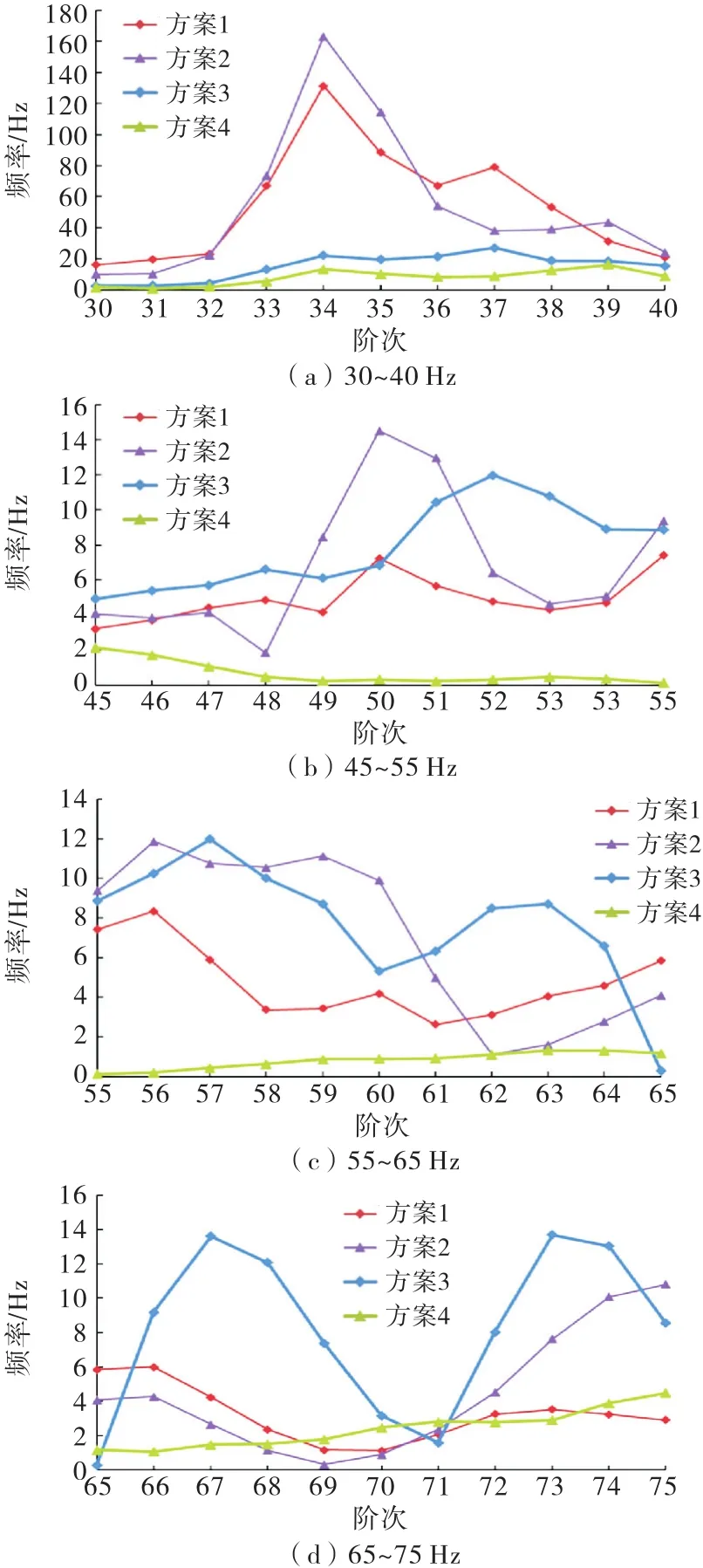
圖9 30～75 Hz頻率范圍內母線層樓梯特征點動位移

從圖中可以看出，樓梯結構的動力響應隨激振頻率顯著變化，前3個方案動位移隨激振頻率的提高交錯變化.在30～40 Hz頻率范圍內，方案1和方案2樓梯結構動位移最大，由于方案1和方案2樓梯結構自振頻率相近，所以誘發(fā)最大動力響應的激振頻率相同，均在34 Hz左右.在45～75 Hz某些頻率范圍內，方案3動位移大于方案1、2，說明增設立柱后局部結構的自振頻率會與激振頻率更加接近.方案4的動位移在幾乎所有頻率范圍內都是4個方案中最小的，且數(shù)值非常小，再次證明在樓梯間增加側墻可以大幅減小樓梯結構的動力響應，抗振效果最佳.且無論采用哪種樓梯結構型式，本工程的轉輪葉片頻率56.25 Hz都不會引起樓梯結構過大的振動響應.

5 結 語

本文對某抽水蓄能電站地下廠房樓梯結構進行了有限元動力分析，研究了踏步對樓梯結構動力特性的影響，并對比分析了4種常用樓梯結構的自振特性和動力響應，主要結論如下:

1)與完整模擬樓梯踏步相比，不模擬樓梯踏步或使用質量單元模擬踏步質量，對樓梯結構自振頻率和動力響應均有一定影響，但后者精度相對更高，模擬效果也比較好，可以作為廠房振動計算時樓梯的簡化模擬方式.

2)樓梯間兩端平臺處設置實體墻對樓梯結構的抗振能力影響甚小，而在樓梯間左右兩側增加側墻或在梯段與平臺連接處增加結構柱的方式可以顯著提高樓梯結構的自振頻率.抗振優(yōu)化設計時，可針對廠房內關鍵的激振頻率，采用上述兩種方式來調控樓梯結構的自振特性.

3)樓梯結構的動力響應隨激振頻率的變化而顯著變化，增設立柱來減小動力響應并非在所有頻率范圍內都有效;在樓梯間側面增加實體墻的方式對于減小樓梯結構的動力響應效果最好，而且適應激振頻率的范圍更廣，是提高廠房樓梯結構抗振的有效措施.