光伏光熱互補發電系統多目標容量優化研究
張博智,盧 妍,譚 晨,周麗霞,丁澤宇,侯宏娟,5
(1.國網冀北電力有限公司計量中心,北京 100045;2.國網冀北電力有限公司秦皇島供電公司,秦皇島 066099;3.國網冀北電力有限公司,北京 100054;4.華北電力大學能源動力與機械工程學院,北京 102206;5.華北電力大學新能源電力系統國家重點實驗室,北京 102206)
煤炭、石油等化石燃料的過度使用造成了嚴重的環境問題。大力發展新能源是保護環境,實現“30·60”雙碳目標的一個關鍵舉措。太陽能作為最具潛力的可再生能源發電方式之一受到了廣泛關注和大力發展。目前,太陽能發電主要有以下2 種型式:一種是光伏發電(photovoltaic,PV),另一種是聚光太陽能熱發電(concentrated solar power,CSP)。其中,光伏發電成本較低,但其受太陽能輻射資源影響較大,輸出功率具有波動性和間歇性。而聚光太陽能熱發電雖受限于較高的投資成本,但由于其通常配置有(相對于電儲能)價格低廉的儲熱設備,可實現較為穩定的功率輸出[1]。太陽能光伏-光熱(PV-CSP)互補發電系統結合了PV 的低成本和CSP 的可調度特性,成為平衡太陽能發電質量和成本的選擇之一。
目前,常見的PV-CSP 互補發電耦合方式有:1)利用PV 向CSP 發電系統的輔助設備供電[2];2)通過對PV 和CSP 電站進行功率分配,為用戶提供穩定電能[3];3)利用PV 系統的散熱,向CSP發電系統提供熱量[4];4)利用分光技術合理分配光伏、光熱所接收的太陽光波長[5]。其中,第2 種僅通過運行和調度手段對PV 和CSP 進行結合的非緊湊式PV-CSP 系統,是目前商業化程度最高的PV-CSP 互補發電方式[6]。本文針對該類PV-CSP 互補發電系統進行研究。
由于非緊湊式PV-CSP 系統內PV 電站和CSP電站相對獨立且技術較為成熟,對該類系統的研究主要集中在容量配置優化[7-10]和運行調度優化[11-12]兩方面。周治等[7]基于青海地區氣象條件和電力負荷對PV-CSP 系統內光伏、光熱容量配比進行了研究,并從電力平衡的角度推薦了1:1 的裝機容量配比。Han 等人[8]采用電加熱器加強PV 電站和CSP電站之間的耦合深度,并討論了關鍵設備容量對互補系統供電可靠性和經濟性的影響。為獲得最低發電成本,陳穎[9]基于遺傳算法對PV-CSP 互補發電系統進行了容量優化,結果表明,運行中互補發電系統輸出功率的設定會影響容量優化結果。綜上所述,針對PV-SCP 系統的容量優化研究已引起學術界的廣泛關注,但目前研究多集中于以經濟性為目標的設備容量優化,而較少考慮互補系統的供電可靠性。然而,供電可靠性是衡量含高比例可再生能源電網能否實施的重要指標。
本文建立了PV-CSP 互補發電系統的數學模型,并提出一種針對PV-CSP 互補發電系統的綜合考慮互補系統供電可靠性及經濟性多目標容量優化方法;基于帶精英策略的非支配排序遺傳算法(non-dominated sorting genetic algorithms-II,NSGA-II),對系統內光伏組件數量、蓄電池容量、儲熱系統容量、鏡場面積和電加熱器額定功率進行了優化,獲得了相應的帕累托最優解集;并在此基礎上,通過理想點法獲得最優折衷解,分析了電負荷及關鍵設備容量參數對PV-CSP 互補發電系統性能的影響。
1 PV-CSP 系統介紹
1.1 光伏光熱互補發電系統
PV-CSP 互補發電系統示意如圖1 所示。該互補發電系統包含光伏發電系統、塔式太陽能熱發電系統、電加熱器以及蓄電池等設備。互補發電系統內光伏和光熱電站除了在電網側進行耦合外,也可通過電加熱器將部分或全部光伏棄光功率回收轉化為熱能存入塔式電站的儲熱系統中,實現光伏和光熱電站之間深度耦合。同時,在互補發電系統中配置蓄電池,有利于穩定光伏電站出力,提高用戶負荷滿足率,但由于電儲能成本較高會增加互補系統的投資成本。
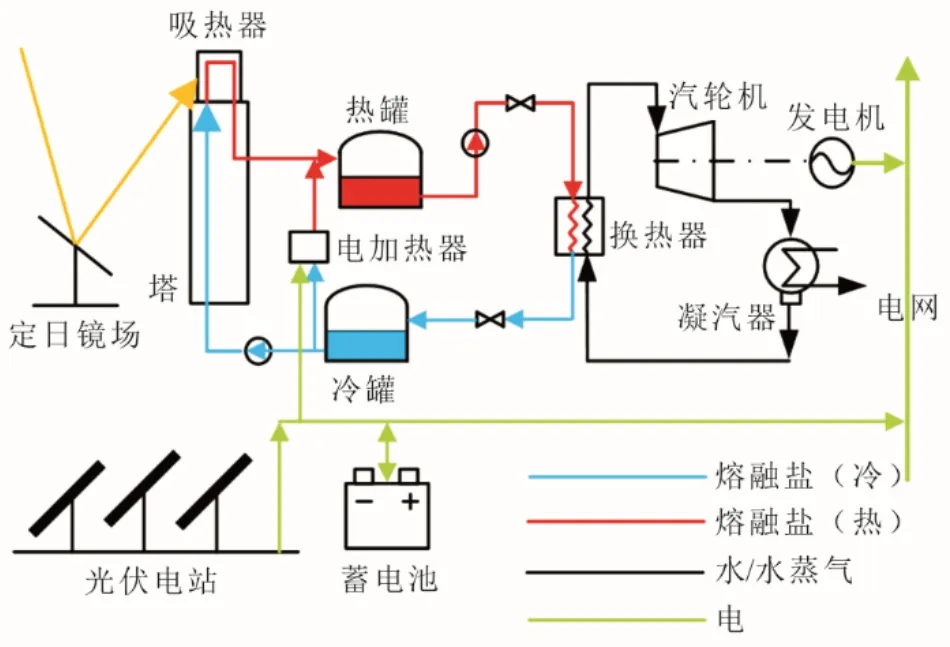
圖1 光伏光熱互補發電系統示意Fig.1 Schematic diagramof the PV-CSP hybrid system
1.2 系統運行策略
互補發電系統的運行策略流程如圖2 所示。與光伏發電相比,光熱電站由于配有較低成本的大規模儲熱系統,可通過儲熱系統對系統出力進行靈活調度,因此互補發電系統在運行過程中優先保證光伏出力。圖2 中Ppv_ideal為光伏理想發電功率,即考慮蓄電池放電后光伏系統最大對外輸出功率;PCSP_ideal為光熱理想發電功率,即考慮儲熱系統放熱后光熱系統最大對外輸出功率;Pload為用戶電負荷。
根據Ppv_ideal、PCSP_ideal和Pload的關系,有以下3 種運行模式。
模式1:光伏發電(含蓄電池放電)和光熱發電(含儲熱系統放熱)無法滿足電網電負荷,均保持當前可能的最大功率輸出。
模式2:單獨光伏出力即可滿足電網電負荷,光熱電站出力為0。此時,若有多余的光伏發電量則將其儲存在蓄電池中,若蓄電池已儲滿,則通過電加熱器轉換為熱能進行儲存。光熱電站內儲熱系統正常運行。
模式3:光伏出力(含蓄電池放電)無法滿足用戶電負荷,所缺電負荷由光熱電站承擔。此時,若光熱電站內有多余太陽能熱則將其存入儲熱系統。
2 光伏光熱互補發電系統模型建立
對光伏光熱互補發電系統進行建模,包括光伏發電系統、塔式太陽能熱發電系統和電加熱器。
2.1 光伏發電系統
2.1.1 光伏組件發電模型
光伏發電系統是通過具有光伏效應的半導體材料將光能轉化為電能。本文對光伏系統的模擬計算參考威斯康星大學太陽能實驗室的光伏發電模型[13]。單個光伏組件的發電功率為:
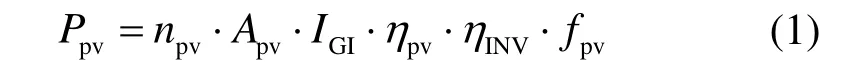
式中:npv為光伏組件個數;Apv為單個光伏組件面積,m2;IGI為光伏組件表面上的總太陽輻射,W/m2;ηINV為逆變器效率,取0.978;fpv為光伏板污染、陰影等損失產生的降額因子,取0.8;ηpv為光伏組件發電效率。ηpv可由下式計算:
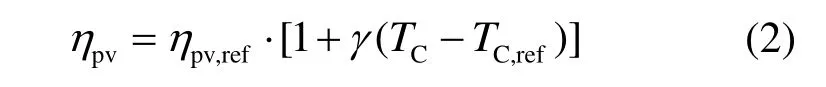
式中:γ為溫度系數,1/℃;TC為光伏組件實際運行溫度;ηpv,ref為標準測試條件下光伏組件效率;TC,ref為標準測試條件下光伏組件運行溫度,℃。標準測試條件為太陽總輻射強度為1 000 W/m2,光伏組件運行溫度為25 ℃。
從式(2)中可知,光伏組件實際運行溫度TC是影響光伏效率的關鍵因素,可由實際運行環境和額定工作溫度條件(太陽總輻射強度為800 W/m2,環境溫度為20 ℃,風速為1 m/s)下電氣參數計算得出:
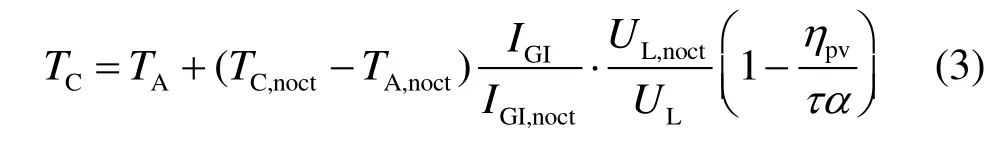
式中:TA為實際運行條件下環境溫度,℃;TC,noct和TA,noct分別為額定工作溫度條件下光伏組件運行溫度和環境溫度,℃;IGI和IGI,noct分別為實際運行條件和額定工作溫度條件下的太陽總輻射強度,W/m2;UL和UL,noct分別為光伏組件散熱系數;τα為光伏組件傳遞吸收因子。
2.1.2 蓄電池模型
t時刻蓄電池的可用電荷量為:
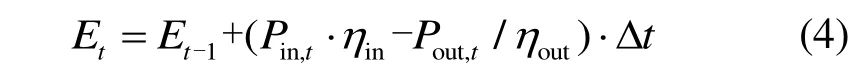
式中:E為蓄電池的可用電荷量,MW·h;Pin和Pout分別為蓄電池充放電功率,MW;ηin和ηout分別為蓄電池充放電效率,取0.94;Δt為仿真時間間隔,取1 h;下標t和t-1 分別為第t時和第t-1 時。
2.2 塔式太陽能熱發電系統
2.2.1 聚光-集熱系統模型
塔式太陽能聚光-集熱系統由定日鏡場、吸熱塔和吸熱器組成,本文采用放射狀柵格法對定日鏡場進行布置,并采用錐體光學法計算鏡場效率。詳細計算方法見文獻[14]。圖3 展示了50 MW 塔式太陽能發電機組在太陽能倍數(solar multiple,SM)為1 時的定日鏡場布置結果。
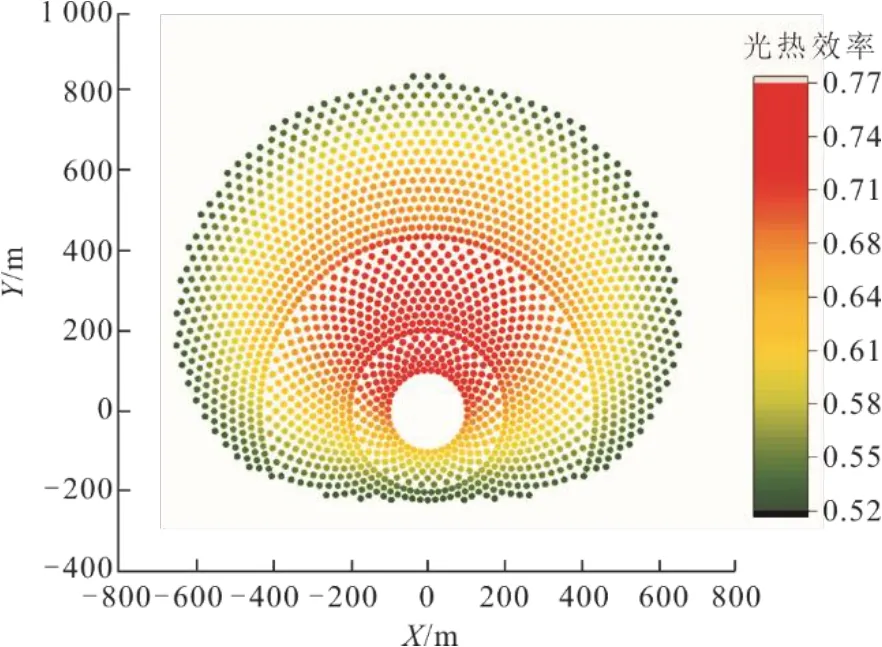
圖3 50 MW 塔式太陽能發電機組定日鏡場布置(SM=1)Fig.3 Layout of the heliostat field of 50 MW solar tower power plant (SM=1)
定日鏡場光學效率ηopt定義如下:
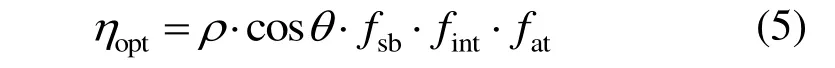
式中:ρ為定日鏡反射效率;cosθ為余弦效率;fsb為定日鏡的陰影遮擋因子;fint為吸熱器的截斷效率;fat為反射光線的大氣透過率。
吸熱器內熔融鹽獲得的熱量為:
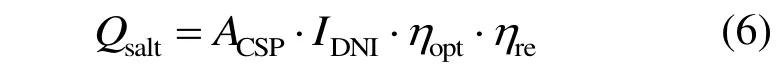
式中:ACSP為定日鏡面積;IDNI為太陽直射輻射強度,W/m2;ηre為吸熱器效率,取0.88。
2.2.2 汽輪機模型
在太陽能熱發電變工況計算過程中,運行工況的變化會引起汽輪機蒸汽流量和主、再熱蒸汽壓力以及各級抽汽壓力發生變化。模型采用弗留格爾公式進行抽汽點壓力計算:
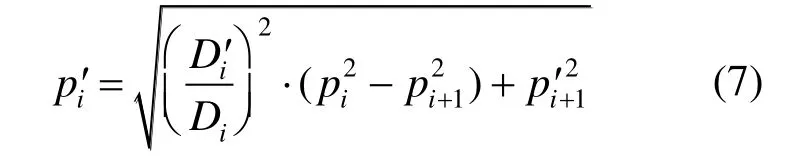
式中:Di和D′分別為變工況前后汽輪機第i級組入口蒸汽流量,kg/s;pi和分別為變工況前后汽輪機第i級組和第i+1 級組抽汽點壓力,MPa。
2.2.3 儲熱系統模型
儲熱系統采用雙罐熔融鹽儲熱。對于塔式太陽能電站,由于熔融鹽直接作為換熱工質且運行溫度較高,采用直接式雙罐熔融鹽儲熱,熱罐熔融鹽溫度為565 ℃,冷罐熔融鹽溫度為280 ℃。t時刻儲熱系統熱平衡關系為:
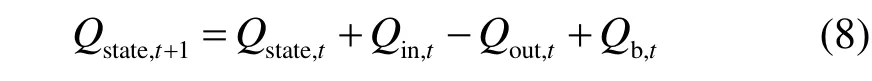
式中:Qstate,t為第t時刻儲熱系統儲存熱量,MW·h;Qstate,t+1為第t+1 時刻儲熱系統儲存熱量,MW·h;Qin,t為第t時刻存入的太陽能熱量,MW·h;Qout,t為第t時刻放出熱量,MW·h;Qb,t為第t時刻電加熱器加熱量,MW·h。
2.3 電加熱器模型
電加熱器可以將棄光電量轉換為熔鹽的熱能并儲存在塔式太陽能電站的儲熱罐中。
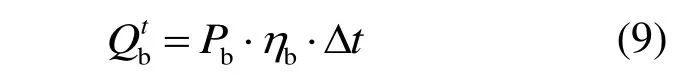
式中:Pb為電加熱器消耗的棄光功率,MW;ηb為電加熱器的效率,取0.98。
2.4 互補發電系統年性能模擬
評估互補發電系統的經濟性和可靠性,需要進行系統年性能模擬。在計算系統年性能時,以系統待優化關鍵設備容量參數和年氣象、負荷數據為輸入,通過1.2 節所述運行策略及本節所建互補發電系統模型對系統逐時光伏發電功率Ppv、光熱發電功率PCSP等運行參數進行計算,模擬流程如圖4 所示。
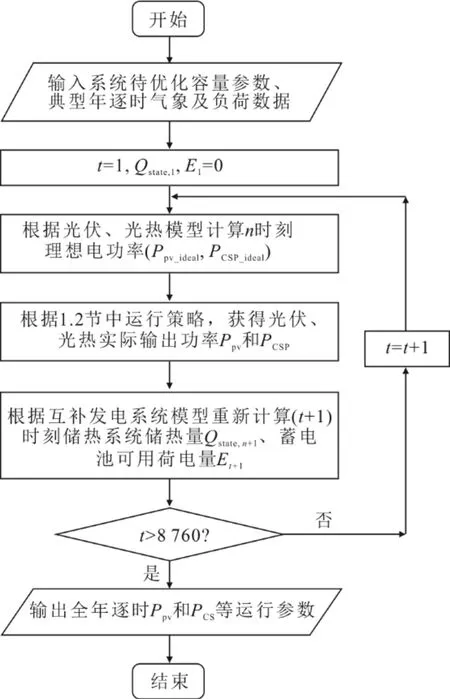
圖4 PV-CSP 互補發電系統年運行性能模擬流程Fig.4 Flow chart of annual operation performance simulation for the PV-CSP hybrid system
3 容量優化模型
3.1 評價指標
本文對于光伏光熱互補發電系統主要從兩方面進行評估,即平準化度電成本和負載缺電率。
3.1.1 平準化度電成本
平準化度電成本(levelized cost of energy,LLCOE)是指在項目生命周期內的發電成本,可用來衡量系統的經濟性[3]:
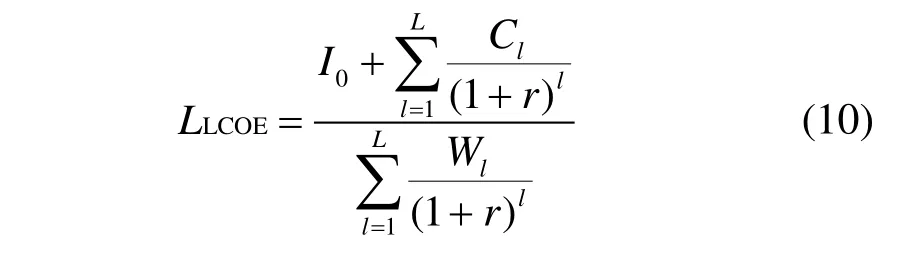
式中:I0為互補發電系統初始投資成本,元;Cl為互補發電系統第l年成本,元;Wl為第l年互補發電系統年發電量,kW·h;r和L分別為折現率(5%)和互補系統壽命(25 年)。
I0、Cl和Wl可由下式計算:
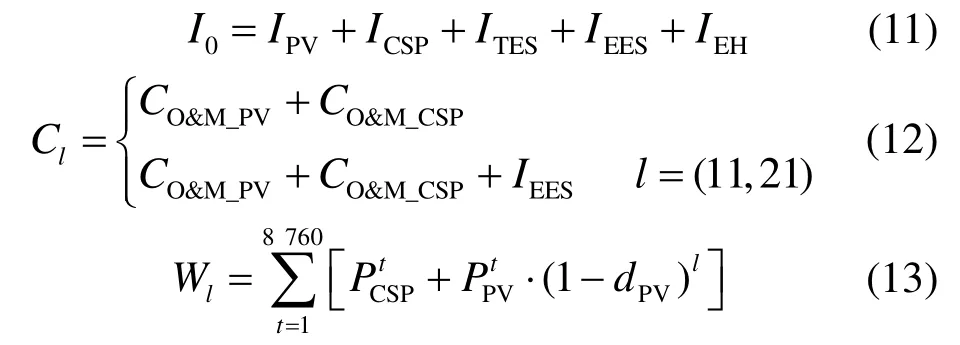
式中:IPV、ICSP、ITES、IEES和IEH分別為光伏、光熱、儲熱、蓄電池和電加熱器的投資成本(元),可由單位功率投資成本(見表1)乘以設備容量計算得出;CO&M_PV和CO&M_CSP分別為光伏和光熱的運維成本,成本數據見表1[8],元;dPV為光伏組件衰減率,取0.6%。本文蓄電池壽命為10 年,因此第11 年和第21 年需要更換蓄電池(式(12))。
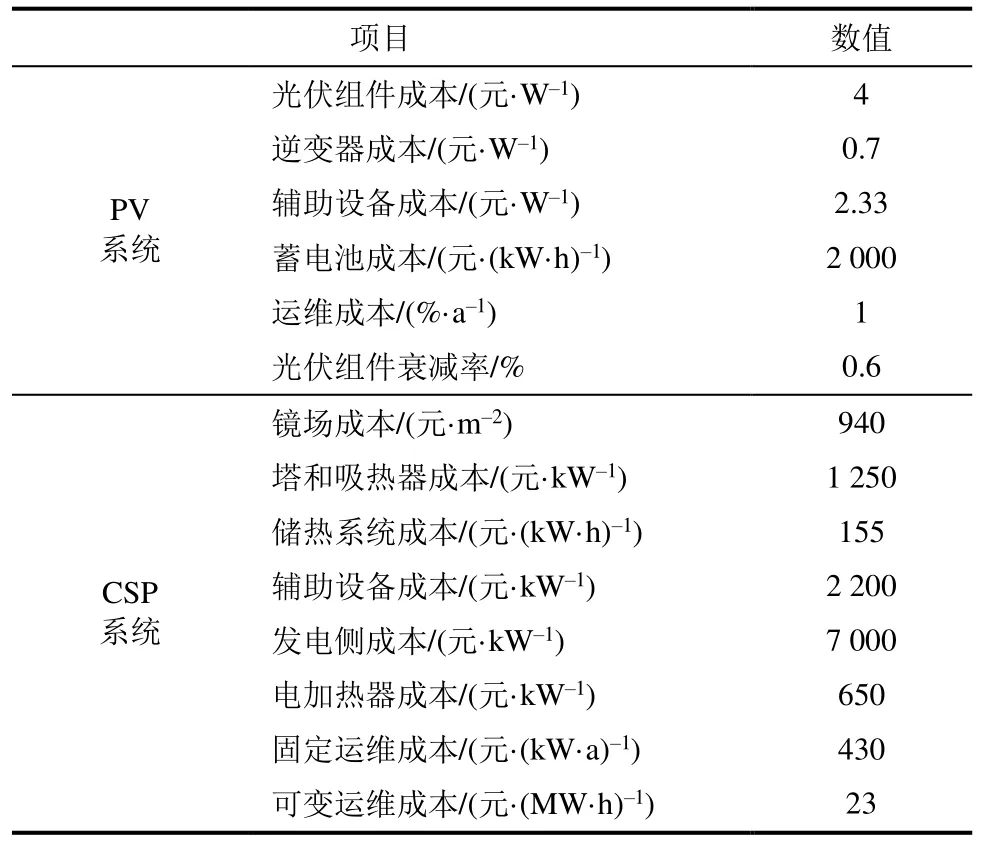
表1 光伏光熱互補發電系統經濟參數Tab.1 Economic parameters of the PV-CSP hybrid system
3.1.2 負載缺電率
互補發電系統在全年的運行中,會出現總輸出并不能很好地滿足用戶負荷的情況。失配情況的時長越多,互補發電系統的可靠性越差,所以需要用負載缺電率來衡量該互補發電系統的可靠性。負載缺電率(loss of power supply probability,LLPSP)可以表示為:
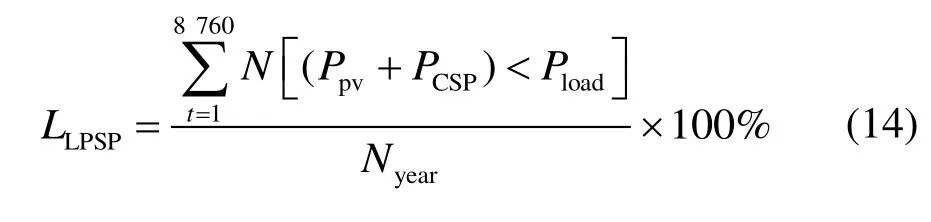
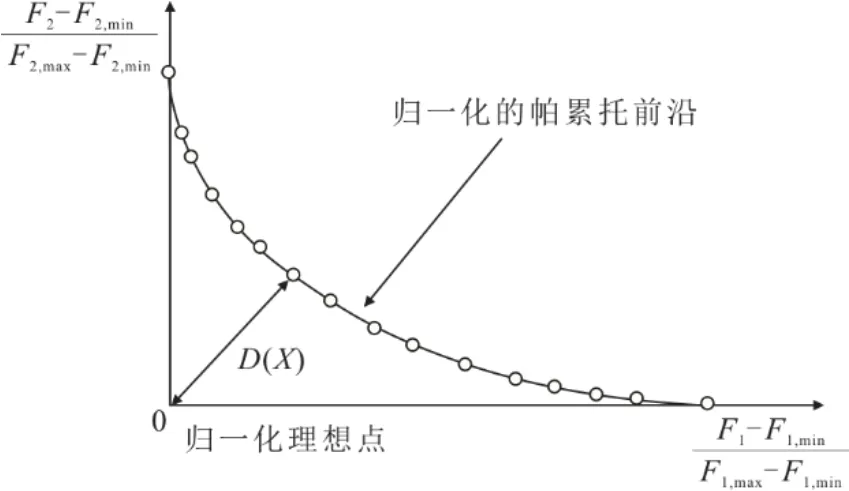
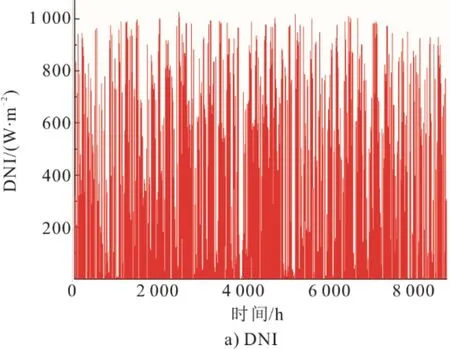
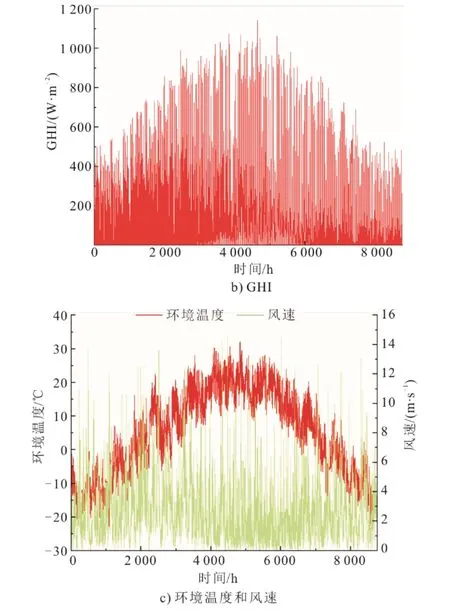
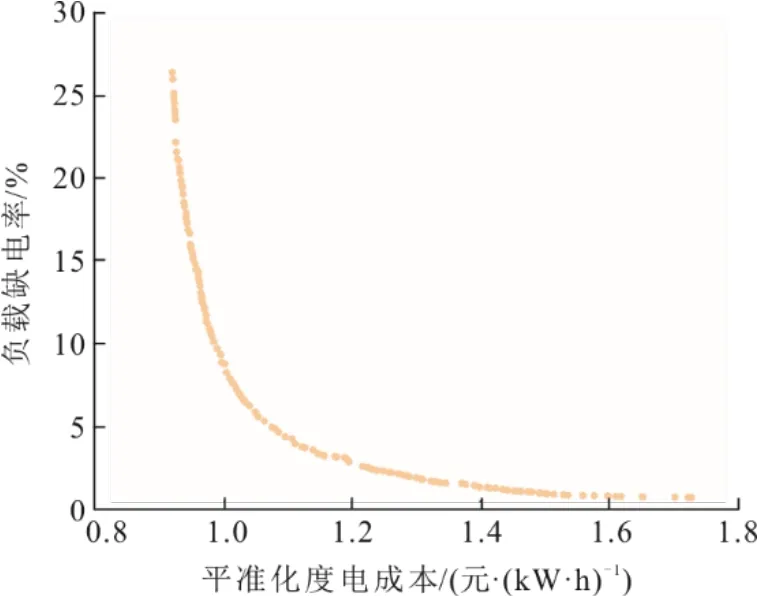
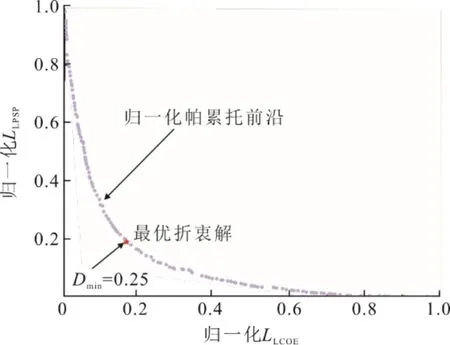
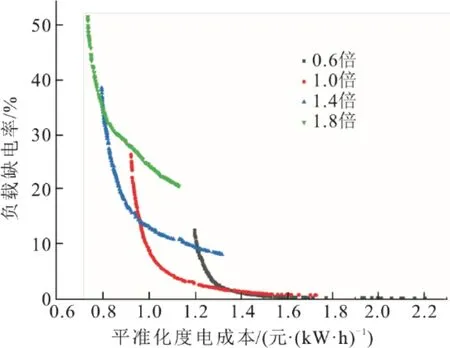
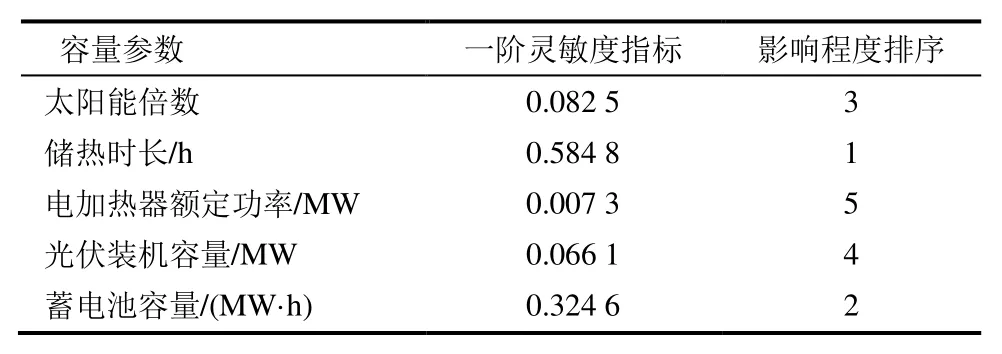
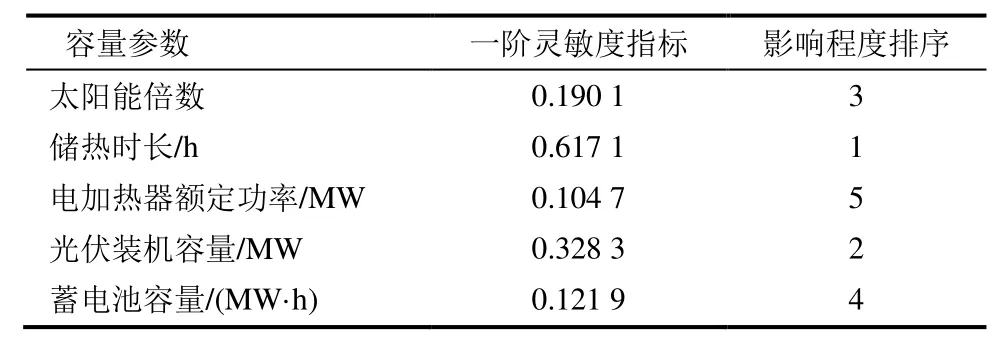
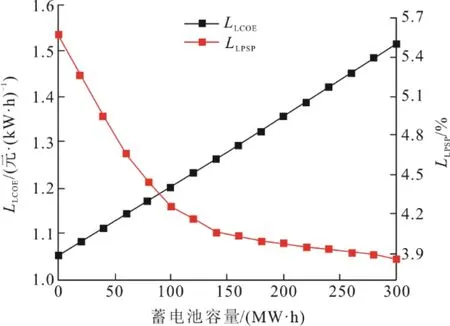
式中:N[(Ppv+PCSP) 為了綜合考慮PV-CSP 互補發電系統供電可靠性和經濟性,本文將負載缺電率和平準化度電成本作為優化目標,采用帶精英策略的非支配排序的遺傳算法(NSGA-II)對PV-CSP 互補發電系統關鍵設備容量進行多目標優化。其容量優化計算流程如圖5 所示。 圖5 基于NSGA-II 的容量優化流程Fig.5 Capacity optimization procedure based on NSGA-II PV-CSP 互補發電系統中待優化的容量參數取值范圍見表2。綜合考慮算法的收斂性和收斂速度,NSGA-II 的迭代次數和種群數量分別取40 和150。 表2 PV-CSP 互補發電系統中關鍵設備容量參數取值范圍Tab.2 Key equipment capacity parameters ranges of the PV-CSP hybrid system 為綜合考慮系統供電可靠性及經濟性,采用理想點法進行容量配置的選擇,獲得最優折衷解。理想點法示意如圖6 所示,其基本思路是選擇帕累托前沿上與理想點Fmin(F1,min,F2,min)幾何距離最近的點作為最優折衷解[15]。幾何距離可由“歸一化距離”表示,其計算方法如下: 圖6 理想點法示意Fig.6 Schematic diagram of the ideal point method 式中:X為帕累托前沿上的點對應的容量配置方案;Fi為第i個目標函數。 以張北地區(東經114.7°,北緯41.2°)某PVCSP 互補發電系統為例,對互補發電系統內光伏裝機容量、蓄電池額定容量、電加熱器額定功率、儲熱系統儲熱時長以及太陽能倍數進行優化研究。張北地區典型年逐時氣象數據如圖7 所示。全年總直射輻射(DNI)為1 729.80 kW·h/m2,總全輻射(GHI)為1 568.33 kW·h/m2。本文采用某50 MVA 變壓器電負荷數據作為互補發電系統承擔的電負荷數據(圖8)。該互補發電系統關鍵設計參數見表3。 圖7 張北地區典型年逐時氣象數據Fig.7 Hourly meteorological data in typical year in Zhangbei 圖8 光伏光熱互補發電系統逐時電負荷Fig.8 Hourly power load of the PV-CSP hybrid system 表3 光伏光熱互補發電系統關鍵設計參數Tab.3 Key design parameters of the PV-CSP hybrid system 基于張北地區氣象及負荷數據和系統設計參數,根據前文所述年性能模擬流程(圖4),采用NSGA-II 算法按圖5 優化流程對案例中PV-CSP 互補發電系統進行優化計算,所得的帕累托最優解集如圖9 所示。從圖9 可知,互補發電系統的LLPSP和LLCOE互相制約。該帕累托前沿線上最左側的點為(0.92,26.38),是互補系統經濟性最優解,其相應的太陽能倍數、電加熱器額定功率、儲熱時長、光伏裝機容量和蓄電池容量分別為1.9 MW、40 MW、12 h、34 MW 和0。該帕累托前沿線上最右側的點為(1.73,0.68),是互補發電系統供電可靠性最優的解,其相應的太陽能倍數、電加熱器額定功率、儲熱時長、光伏裝機容量和蓄電池容量分別為2.9 MW、36 MW、20 h、150 MW 和271 MW·h。 圖9 PV-CSP 互補發電系統容量優化的帕累托最優解集Fig.9 Pareto optimal schemes for capacity optimization of the PV-CSP hybrid system 對于經濟性最優解,互補發電系統的平準化度電成本LLCOE為0.92 元,但其負載缺電率LLPSP高達26.38%,供電可靠性差。而對于供電可靠性最優解,互補發電系統的LLPSP降低至0.68%,但其成本也大幅提升,LLCOE為1.73 元,超過了目前單獨光熱電站標桿上網電價(1.15 元)。因此,本文采用理想點法,綜合考慮互補發電系統經濟性和供電可靠性,獲得了相應的最優折衷解。計算獲得的歸一化帕累托前沿和最優折衷解如圖10 所示。 圖10 歸一化帕累托前沿和最優折中解Fig.10 Normalized Pareto front and optimal compromise solution 最優折衷解對應的LLPSP和LLCOE分別為1.06 元/(kW·h)和5.57%,其相應的太陽能倍數、電加熱器額定功率、儲熱時長、光伏裝機容量和蓄電池容量分別為2.5 MW、74 MW、20 h、82 MW 和0。 4.3.1 電負荷變化 為了分析電負荷的變化對PV-CSP 互補發電系統容量優化結果影響,本文通過對50 MVA 變壓器電負荷按比例放大、縮小來改變互補發電系統所承擔電負荷,并對不同電負荷條件下互補發電系統的容量參數進行優化。優化獲得的帕累托最優解集和最優折衷解分別如圖11 和表4 所示。 圖11 不同電負荷條件下PV-CSP 互補發電系統容量優化帕累托最優解集Fig.11 Pareto optimal schemes for capacity optimization of the PV-CSP hybrid system at different power loads 表4 不同電負荷條件下PV-CSP 互補發電系統容量優化最優折衷解Tab.4 Optimal compromise solution for capacity optimization of the PV-CSP hybrid system at different power loads 從圖11 可以看出,互補發電系統所承擔的電負荷越大,帕累托前沿曲線上的最小LLCOE越小,而最小LLPSP越大。這是由于電負荷的增大增加了互補發電系統的發電空間,相同容量參數下互補發電系統發電量提高,因而經濟性變好。但是發電空間的增加也增加了互補發電系統不滿足負荷需求的時間。尤其是當互補發電系統承擔的電負荷超過50 MW 時,超出的部分無法單獨通過光熱機組來滿足,互補發電系統的供電可靠性大幅下降(如圖11中1.4 倍和1.8 倍電負荷所示)。綜合表4 中的不同電負荷條件下的最優折衷解對應的LLCOE和LLPSP,在本文案例所對應的資源和電負荷條件下,推薦采用互補發電系統中CSP電站的額定發電功率作為互補發電系統承擔的電負荷。 4.3.2 容量參數變化 本節采用Saltelli 提出的一階靈敏度指標Sk來量化容量參數對系統經濟性和供電可靠性的影響,并進行排序。一階靈敏度指標的詳細計算方法見文獻[16]。容量參數對系統LLCOE和LLPSP的影響程度分別見表5 和表6。在最優折衷解容量配置下,互補發電系統LLCOE和LLPSP隨蓄電池容量變化情況如圖12 所示。從表5 和表6 可以看出,CSP 電站內儲熱系統的儲熱時長是對PV-CSP 互補發電系統經濟性和供電可靠性影響最大的容量參數。因此,在進行PV-CSP 系統設計時,應優先考慮調整儲熱系統儲熱量。由圖12 可見,對于互補發電系統LLCOE,蓄電池容量是影響程度第二的容量參數。蓄電池容量由0 增加到300 MW·h 時,互補發電系統的LLCOE由1.05 元/(kW·h)增加到1.51 元/(kW·h)。另一方面,蓄電池容量對LLPSP影響較小。蓄電池容量由0 增加到300 MW·h 時,互補發電系統的LLPSP僅由5.58%降低到了3.86%。因此,互補發電系統優化結果中,為降低互補發電系統LLCOE蓄電池容量基本為0。對于互補發電系統的LLPSP,光伏裝機容量是影響程度第二的容量參數,增加光伏裝機容量會降低互補發電系統的LLPSP。 表5 PV-CSP 互補發電系統容量參數對LLCOE 影響排序Tab.5 Factor prioritizations of capacity parameters for LLCOE of the PV-CSP hybrid system 表6 PV-CSP 互補發電系統容量參數對LLPSP 影響排序Tab.6 Factor prioritizations of capacity parameters for LLCOE of the PV-CSP hybrid system 圖12 最優折衷解配置條件下PV-CSP 互補發電系統LLCOE和LLPSP 隨蓄電池的變化情況Fig.12 The variation of LLCOE and LLPSP of the PV-CSP hybrid system with accumulator capacity based on optimal compromise solution configuration 1)本文提出一種針對光伏光熱(PV-CSP)互補發電系統的多目標容量優化方法,旨在尋找綜合考慮互補發電系統平準化度電成本(LLCOE)和負載缺電率(LLPSP)的最優折衷解。 2)以張北地區的PV-CSP 互補發電系統為例,本文采用所提優化方法對其進行了容量優化,獲得了帕累托最優解集,進而通過理想點法獲得了最優折衷解。最優折衷解對應的互補發電系統LLCOE和LLPSP分別為1.05 元/(kW·h)和5.57%,相應的太陽能倍數、電加熱器額定功率、儲熱時長、光伏裝機容量和蓄電池容量分別為2.5 MW、46 MW、20 h、82 MW 和0。 3)增加互補發電系統所承擔電負荷可以降低LLCOE,但會增加LLPSP。對于LLCOE,容量參數影響程度順序為:儲熱時長>蓄電池容量>太陽能倍數>光伏裝機容量>電加熱器額定功率。對于LLPSP,容量參數影響程度順序為:儲熱時長>光伏裝機容量>太陽能倍數>蓄電池容量>電加熱器額定功率。3.2 優化算法


3.3 理想點法
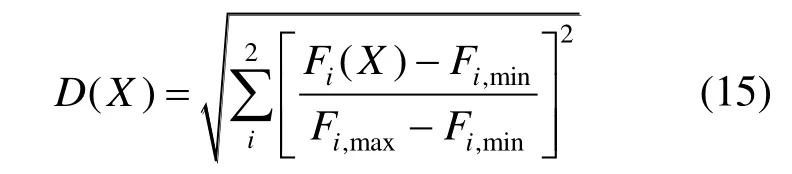
4 案例分析
4.1 案例描述
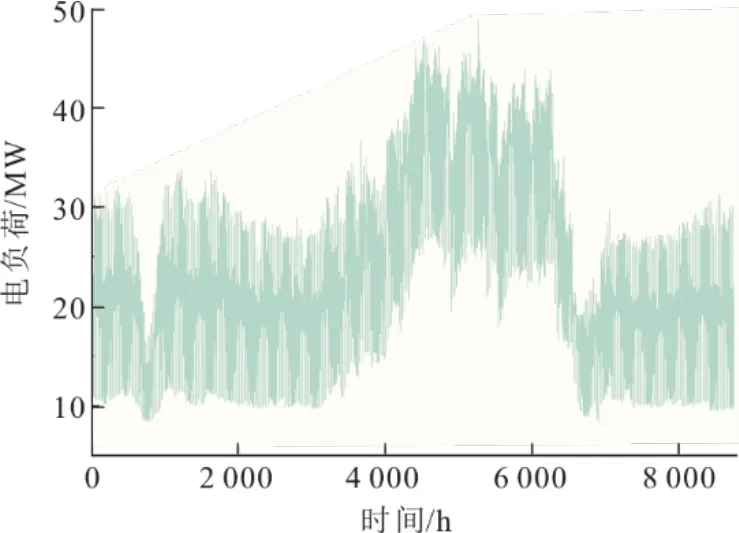

4.2 優化結果
4.3 敏感性分析

5 結論

