基于響應面法的動力引鞋驅動渦輪性能研究*

羅光福 張 紅 蔣勇銘 馮 定

(1.長江大學機械工程學院 2.湖北省油氣鉆完井工具工程技術研究中心 3.中國石油青海油田井下公司)

0 引 言

水力驅動渦輪引鞋是一種新型水力驅動的井下下套管裝置，具有高速擴眼、修整井壁、降低功率消耗和減少發生套管下入事故的可能性等優點，有著廣泛的應用前景，其相關研究推動了國內外渦輪鉆井技術的蓬勃發展[1-2]。渦輪是水力驅動渦輪引鞋工具的動力環節，當流體流經渦輪時，流體驅動渦輪旋轉產生扭矩，從而帶動主軸一起轉動來實現工具功能，起到將流體介質的液體能轉化為主軸上機械能的作用，是工具中的重要部分。

近年來，井下工具中的渦輪一直是研究的熱點，國內外學者已經開展了大量研究，主要集中在渦輪葉片型線的設計[3-5]、渦輪葉片參數化設計與優化[6-8]、渦輪的水力性能分析與研究[9-14]等方面。但是，對于渦輪水力性能的研究大都通過參數單因素敏感性來分析，缺乏關于各因素對水力性能影響程度的系統性研究，關于渦輪受流體作用下的受力行為研究也較少。

為此，本文以水力驅動渦輪引鞋工具的渦輪為研究對象，考慮渦輪與流體之間的流固耦合作用，利用有限元方法對相關參數進行單因素敏感性分析并篩選影響較大參數；然后建立關于渦輪水力效率和等效應力的多因素多水平的響應面分析模型；最后擬合對應的回歸方程。研究結果可為水力驅動渦輪引鞋工具的設計提供理論依據，還可為渦輪的流固耦合相關研究提供參考。

1 技術分析

1.1 水力驅動渦輪引鞋結構及工作原理

水力驅動渦輪引鞋工具包括支承節部分和動力轉換部分，其結構如圖1所示。支承節部分由徑向軸承和推力軸承組組成，動力轉換部分由渦輪定子和渦輪轉子組成[15]。

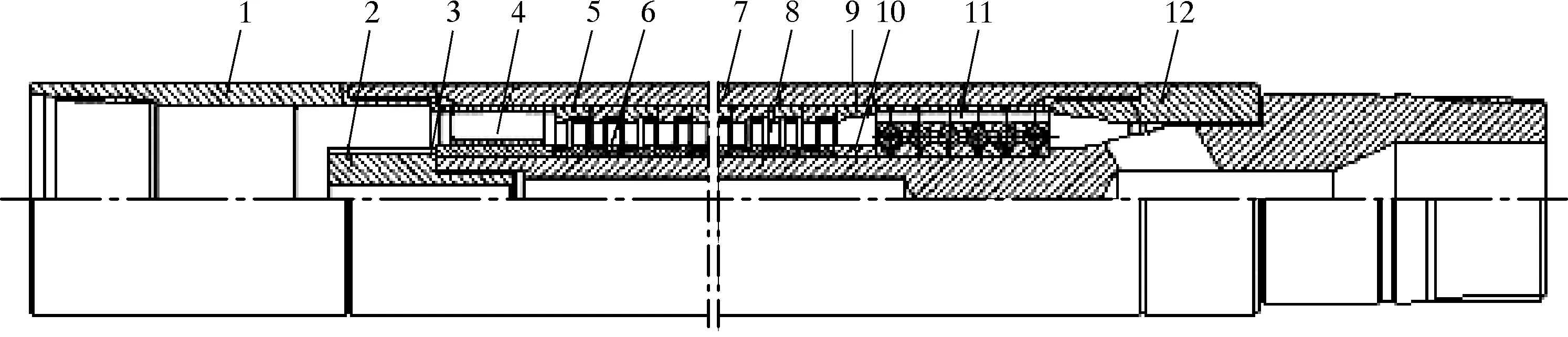
1—上接頭;2—壓緊短節;3—套筒;4—徑向軸承;5—渦輪定子;6—渦輪轉子;7—殼 體;8—渦輪軸;9—擋流裝置內圈;10—擋流裝置外圈;11—推力軸承組;12—下短節。圖1 渦輪引鞋整體結構圖Fig.1 Structure of turbine guide shoe

水力驅動渦輪引鞋工具的動力轉換部分由50組渦輪定子和轉子組成。流體介質通過渦輪定子和轉子，與轉子葉片相互作用，單位時間內流體介質的動量矩改變，使轉子獲得工作扭矩，實現將流體介質的液體能轉化為主軸上的機械能，從而驅動引鞋頭轉動來實現其功能。圖2為渦輪工作情況圖。

1.2 水力效率計算及強度校核

根據一級渦輪的壓力降和轉化扭矩計算渦輪的水力效率，即有：

η=2πnΜ/(LΔp)

(1)

式中：η為一級渦輪的水力效率；n為轉速，r/min；Μ為一級渦輪的轉化扭矩，N·m；L為流體介質的流量，m3/min；Δp為一級渦輪的壓力降，MPa。

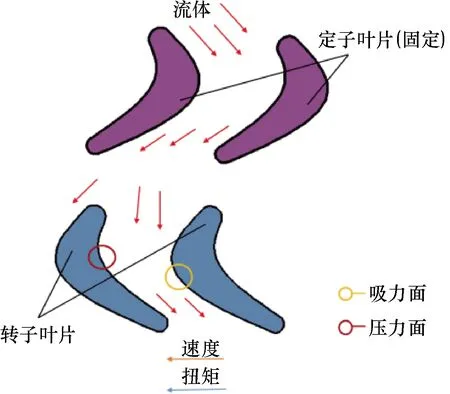
圖2 渦輪工作情況示意圖Fig.2 Schematic diagram of turbine working

采用第四強度理論對渦輪進行強度校核，即：

[σ]

(2)

式中：σr4為基于第四強度理論計算的相當應力，MPa；σ1、σ2、σ3分別為危險點處3個主應力，MPa；[σ]為材料的許用應力，MPa。

2 渦輪有限元分析

采用Fluent與Workbench聯合仿真方法，研究流固耦合作用下的渦輪水力性能和受力規律。由于流體作用下渦輪葉片的應變較小，對流域的影響可忽略，所以采用單向流固耦合方法模擬渦輪受流體沖擊時的受力狀態。

2.1 物理模型及網格劃分

2.1.1 物理模型

為降低計算誤差，模擬渦輪實際受力狀態，本文采用三維模型的方法，渦輪的流道模型及實體模型如圖3所示。

圖3 渦輪模型Fig.3 Turbine model

2.1.2 網格劃分

計算分析前，先進行網格無關性分析來檢驗網格的獨立性。針對流道模型，對網格數量分別為1 078 468、1 321 933、1 559 179、1 790 825和2 079 857的結構進行數值模擬分析，得出當網格數量增加至1 559 179時，渦輪的水力效率基本不隨網格數量的變化而變化。考慮到計算精度和計算成本，本文最終選取網格數量為1 559 179的結構進行數值模擬分析。對于實體模型，對網格數量分別為1 701 514、2 050 803、2 510 803和3 312 262的結構進行數值模擬分析，同理，最終選取網格數量為2 510 803的結構進行數值模擬分析。

綜合考慮計算精度和計算成本，進、出口流道采用六面體和四面體混合網格劃分，渦輪采用多面體網格。單副渦輪流道模型的網格劃分如圖4所示。

圖4 流道模型網格劃分示意圖Fig.4 Mesh division of turbine runner model

對于渦輪三維模型采用自由網格劃分方法，并在定轉子葉片兩端給予局部加密。單副渦輪實體模型網格劃分如圖5所示。

圖5 實體模型網格劃分示意圖Fig.5 Mesh division of turbine solid model

2.2 邊界條件

在流體仿真中，渦輪的流道模型分為4部分，分別為進口流道、定子流道、轉子流道和出口流道，屬于多區域計算模型，在各區域分界面設置interface實現計算傳遞。進口采用速度進口，出口采用outflow邊界條件；定義轉子流域速度；在渦輪組進、出口和轉子葉片上設定監視器，監視渦輪組進、出口壓力變化和轉子旋轉過程中的扭矩變化。

在靜力學仿真中，渦輪材料選用灰鑄鐵，彈性模量為120 MPa，泊松比為0.25，密度為7 340 kg/m3，抗拉強度為200 MPa。將定子外圈和轉子內圈設定為固定約束,設置轉子的轉動速度,將Fluent計算的葉片所受壓力值作為輸入載荷。

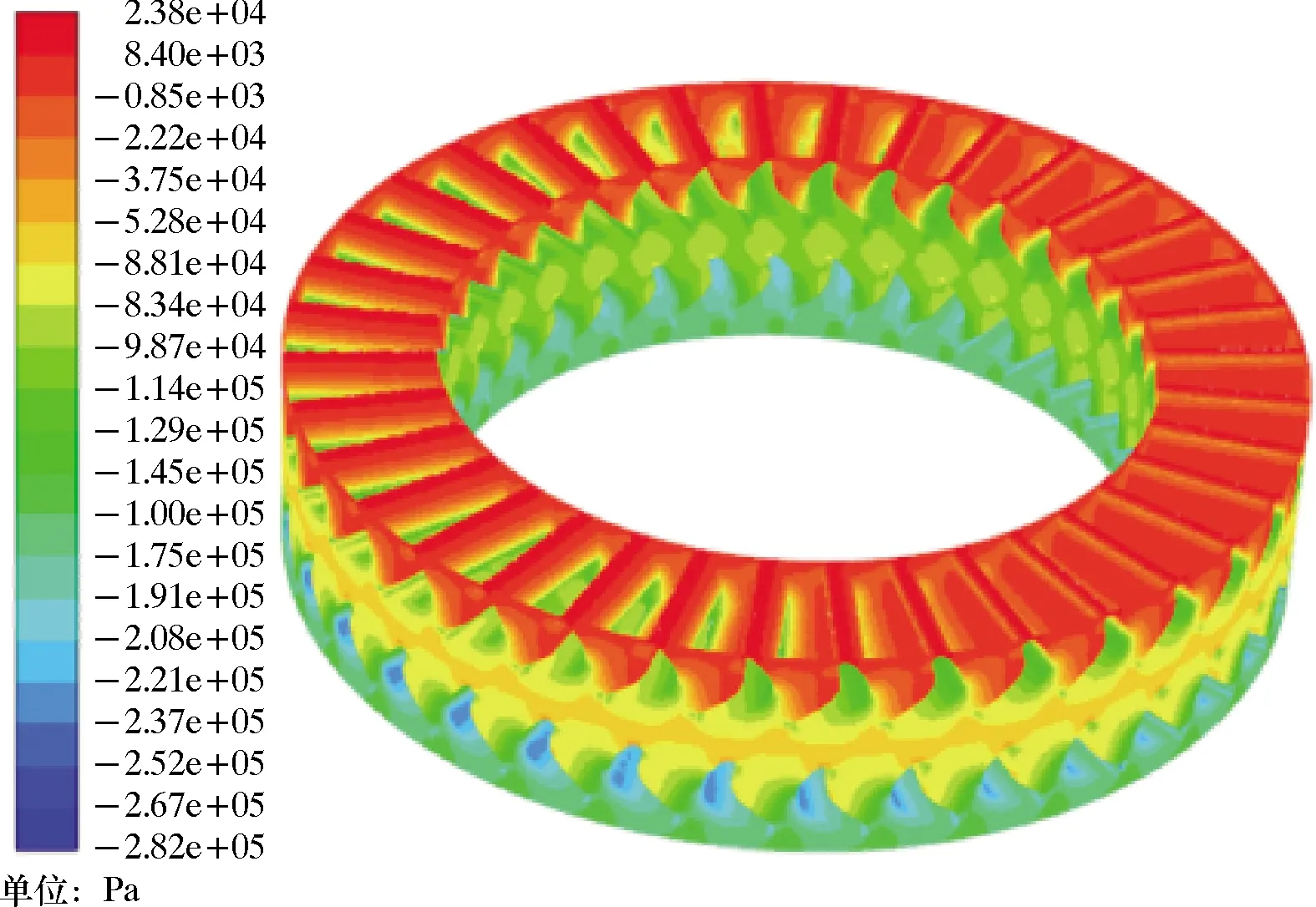
圖6 渦輪定轉子壓力云圖Fig.6 Cloud chart of pressure on turbine stator and rotor

2.3 結果分析

利用Fluent有限元軟件對渦輪組進行數值模擬，計算渦輪組的壓力降和扭矩。如圖6為渦輪定轉子的壓力場云圖。從圖6可以看出，壓力場由上至下數值呈梯度變化，在葉片壓力面處壓力較大，在吸力面處壓力驟降。圖7是一級渦輪轉化扭矩隨時域的變化曲線。流體進入渦輪組后，渦輪受流體沖擊開始旋轉，產生一定扭矩，當渦輪穩定旋轉后，由于定子與轉子之間的流域周期性改變，產生的扭矩也對應周期波動。

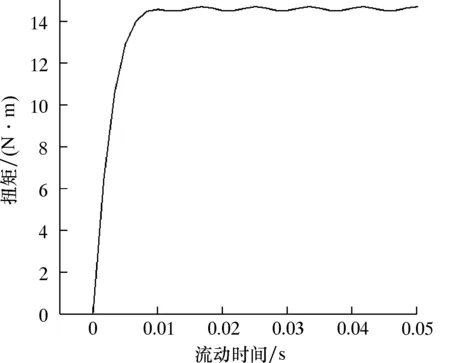
圖7 一級渦輪轉化扭矩隨時域變化曲線Fig.7 Changes of torque of first-stage turbine with time

通過聯合Fluent和靜力學模塊，進行流固耦合計算，顯現渦輪受到流體沖擊效果，渦輪轉子的等效應力云圖如圖8所示。由圖8可以發現，最大等效應力發生在轉子葉片根部，且向著外側逐漸減小。這是因為流體介質通過沖擊轉子葉片帶動轉子旋轉，產生離心力，在離心力的作用下，流體被甩入葉片外側。再者由于轉子內圈裝配在主軸上并將帶動主軸旋轉，受到來自主軸的約束，而轉子外圈的約束取決于內圈，使得轉子葉片類似于懸臂梁的結構，所以應力集中于葉片根部。

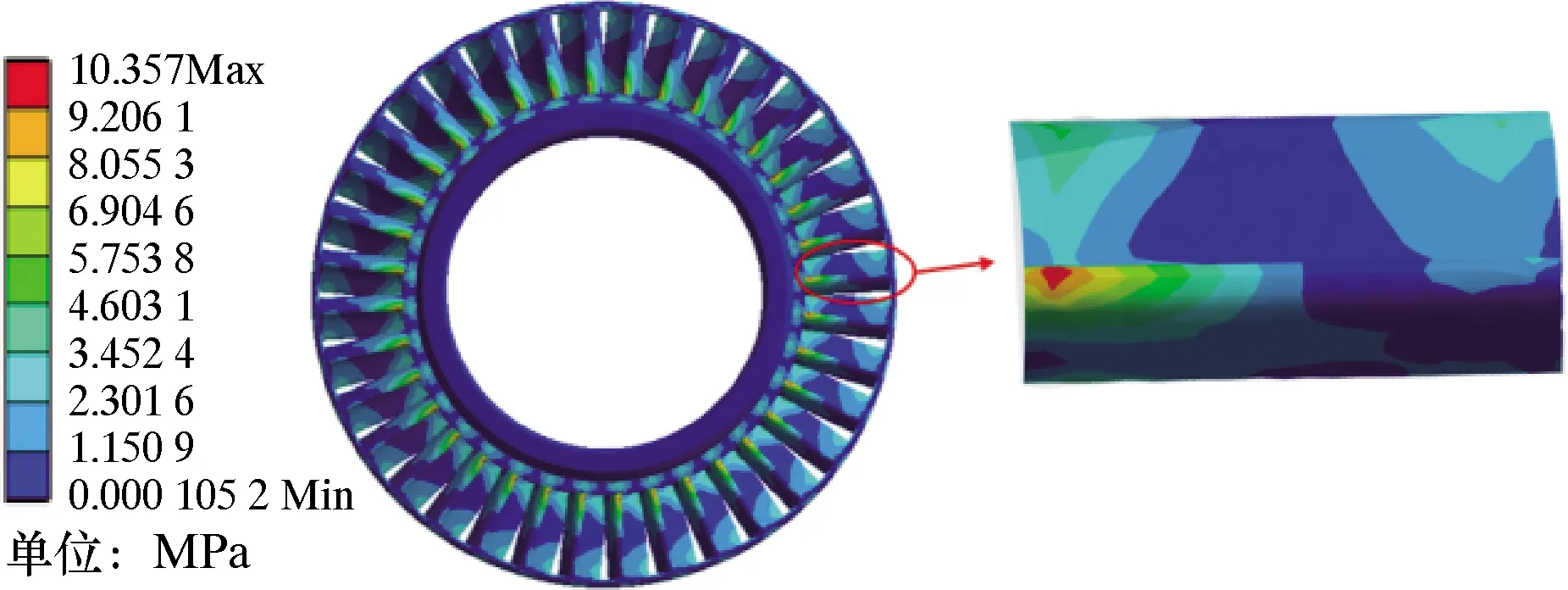
圖8 渦輪轉子等效應力云圖Fig.8 Cloud chart of equivalent stress of turbine rotor

3 單因素分析

為研究水力驅動渦輪引鞋工具的渦輪組的工作參數(流體流量及流體密度)和結構參數(渦輪定轉子葉片數及渦輪定轉子軸向間隙)對其水力效率和最大等效應力的影響規律，基于流固耦合仿真方法，采用單因素分析法，分別對流體的流量、密度、渦輪定轉子葉片數和渦輪定轉子軸向間隙這4個因素的敏感程度進行研究，根據單因素分析結果確定敏感因素及其取值范圍。圖9為各單因素與渦輪水力效率及最大等效應力的規律曲線。

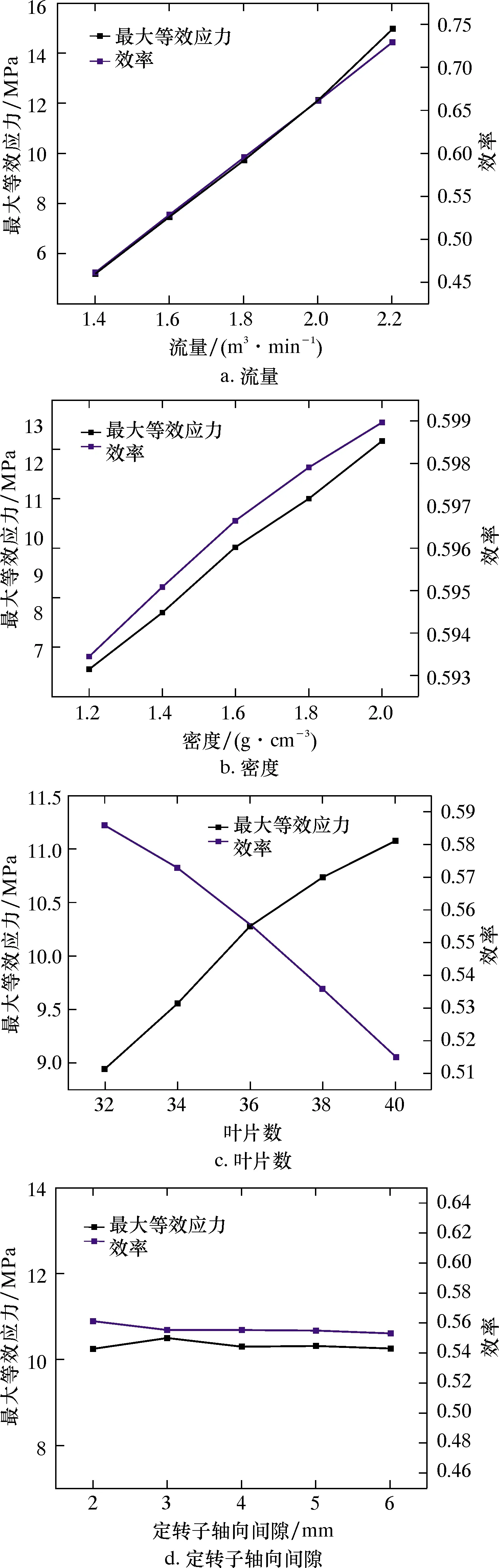
圖9 各單因素與渦輪水力效率及最大等效應 力的規律曲線Fig.9 Effects of each single factor on turbine hydraulic efficiency and maximum equivalent stress

根據實際工況，對設計參數的取值范圍進行初選，具體取值如下：流體密度1.2～2.0 g/cm3，流體流量1.4～2.2 m3/min，渦輪定轉子葉片數32～40，渦輪定轉子軸向間隙2～6 mm。

由圖9可知：在初選的取值范圍內，流體的流量、密度和渦輪定轉子葉片數對渦輪的水力效率和最大等效應力影響較大；渦輪定轉子軸向間隙對其影響很小，間隙從2 mm變化至6 mm，效率降低了1.4%，最大等效應力降低了2.1%。因此，綜合分析后選取流體的流量、密度和渦輪的葉片數作為設計變量，分別記為A、B、C，并將初選的設計參數的取值范圍作為設計變量的取值范圍。

4 響應面分析

4.1 試驗設計

基于Box-Behnken試驗設計[16]方法生成3因素3水平共29個試驗設計點，試驗設計表及計算結果如表1所示。

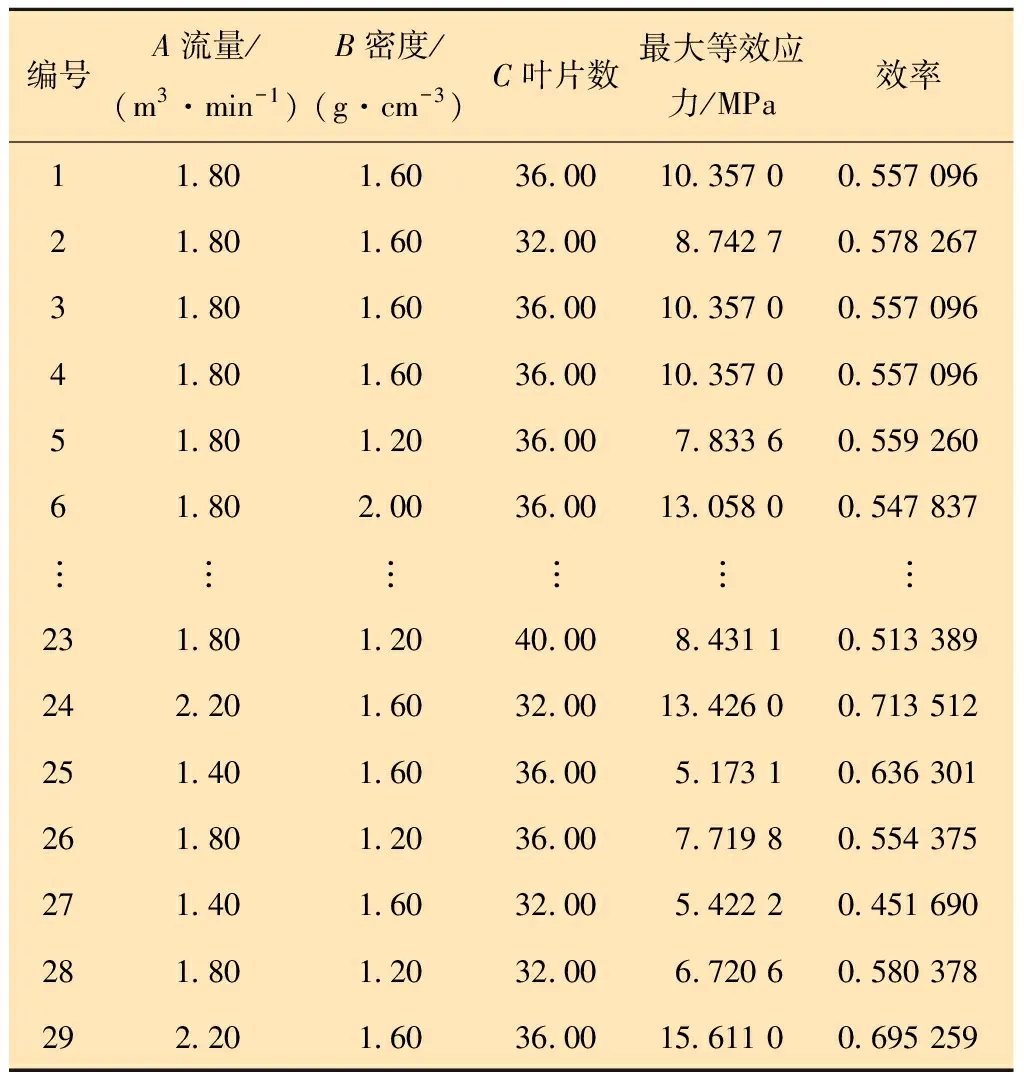
表1 Box-Behnken試驗設計點及計算結果Table 1 Design points and calculation results of Box-Behnken test

4.2 方差分析

表2是渦輪最大等效應力的二次響應面模型和方差分析表。由表2可知，該模型的P值小于0.000 1，表示非常顯著，所建立的響應面模型可用；各一次項系數和二次項系數(A、B、C、AB)的影響非常顯著。該模型的R2=0.988 2，說明該模型的擬合度較好，預測的R2值與調整后的R2值接近于1，說明預測模型精度較高，差值小于0.2，信噪比為51.16，大于4，表明信號足夠，該模型可用于預測。

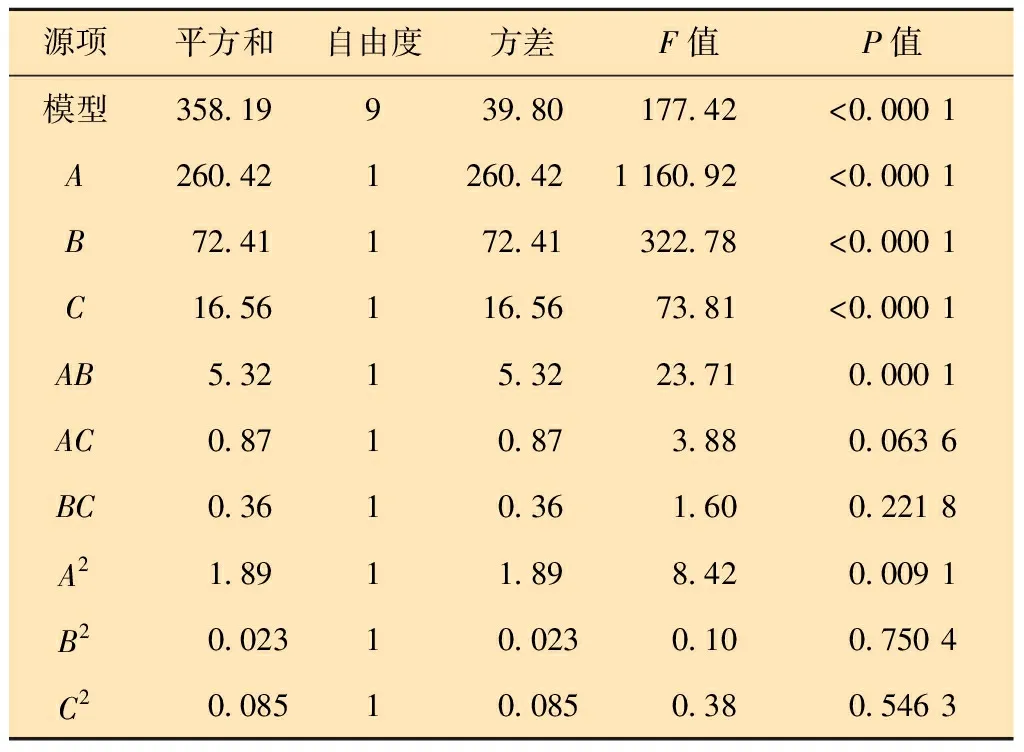
表2 最大等效應力的二次響應面模型和方差分析Table 2 Quadratic response surface model and variance analysis of maximum equivalent stress

以渦輪的水力效率η和最大等效應力σ為響應值，對試驗結果進行二次多項回歸擬合，各因素與響應值之間的關系可用二次多元回歸方程表示，具體如下：

η=-0.57+0.20A-0.002 999B-0.062C-

0.000 207 8AB+0.004 871A2-0.027B2-

0.000 340 3AC-0.000 459 2BC-0.037C2

(3)

σ=10.21+4.66A+2.46B+1.17C+

1.15AB+0.47AC+0.30BC+0.53A2-

0.059B2-0.11C2

(4)

式(3)和式(4)中，單因素(A、B、C)前面的系數可以反映該因素對目標值的影響程度，系數越大表示影響程度越大。通過擬合方程可以直接計算出目標值，省去了模擬仿真的計算成本。借助該數學模型，可以與渦輪的一些設計計算結合，為渦輪的結構設計及優化提供參考。

圖10為渦輪的水力效率、最大等效應力與流體流量和密度之間的響應面圖。從圖10可以發現：當流量從1.4 m3/min增加到2.2 m3/min，渦輪的水力效率增加了58.41%，最大等效應力增加了146.81%；當流體密度從1.2 g/m3增加到2.0 g/m3，渦輪水力效率增加了0.80%，最大等效應力增加了66.20%；當渦輪葉片數從32增加到40，渦輪水力效率降低了12.17%，最大等效應力增大了23.91%。通過響應面模型可以直觀地看出因素與響應之間的變化關系。為了方便觀察設計變量對渦輪的最大等效應力和渦輪水力效率的影響規律，對各變量的影響規律進行總結，結果如表3所示。

圖10 目標變量與設計變量響應面圖Fig.10 Response surface diagram of target variables and design variables

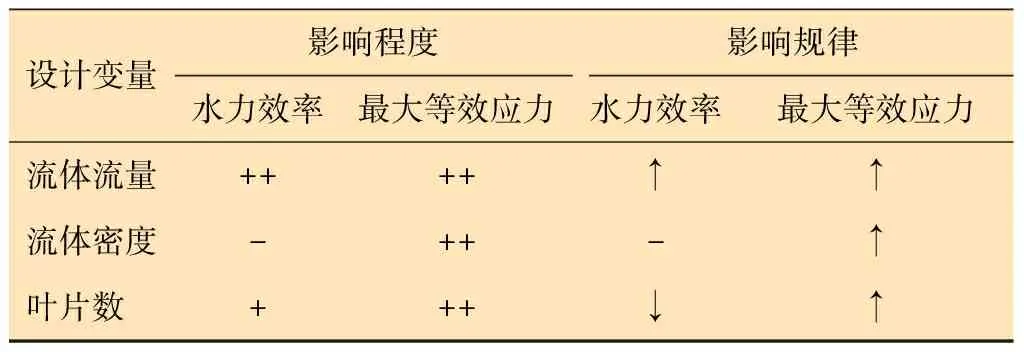
表3 設計變量的影響規律Table 3 Influence rules of design variables

5 結 論

本文基于流固耦合的方法對水力驅動渦輪引鞋工具的渦輪進行仿真分析，采用單因素分析法確定了渦輪的敏感因素及其取值范圍，基于Box-Behnken方法進行試驗設計，并建立響應面模型，以渦輪的敏感因素為設計變量，對渦輪的水力性能和最大等效應力進行研究，得出以下結論：

(1)工作工況下，渦輪最大等效應力發生在渦輪轉子葉片根部，且應力由根部向另一端遞減。

(2)對流體流量和密度、渦輪定轉子葉片數和渦輪定轉子軸向間隙進行分組試驗，確定流體流量、流體密度和渦輪定轉子葉片數為設計變量，并確定了它們的取值范圍。

(3)建立的渦輪最大等效應力和水力效率與設計變量的響應面模型具有較高的擬合精度，滿足計算要求，并得到相應的回歸方程。

(4)渦輪的水力效率受流體的流量影響較大且隨著流量的增大而增大，增幅為58.41%；受渦輪定轉子葉片數影響較小并隨著葉片數的增加而減小，增幅為-12.17%；而流體密度對其幾乎無影響，增幅僅為0.80%。

(5)渦輪轉子的最大等效應力受流體流量、流體密度與渦輪定轉子葉片數的影響顯著，并隨著這些因素的增大而呈現正增長趨勢，增幅分別為146.81%、66.20%和23.91%。