聚合物纖維網面層加固砌體的粘結本構模型
初圣林,吳鋒
(大連交通大學 土木工程學院,遼寧 大連 116028)
外貼聚合物纖維復合材料是增強砌體結構性能的有效措施,具有高比強度、耐腐蝕、抗疲勞等諸多優點.這種加固方法主要是利用兩種材料拉壓協調互補的共同作用,構成一個力學性能更加優異的結構體系.當纖維材料加固的砌體構件受力時,荷載會通過纖維材料與砌體間的粘結面傳遞,因此纖維材料的增強效率取決于粘結面的性能[1].
纖維材料和砌體間的粘結作用比較復雜,主要由膠結力和摩阻力組成.纖維面層加固砌體在拉拔作用下的典型破壞模式為纖維材料粘結層連帶部分砌體表面剝離的破壞形式[2].在該模式下,依據Yuan和Teng的粘結滑移模型[3],荷載滑移曲線在纖維材料達到極限滑移后開始剝離,剝離過程中宏觀極限拉力保持不變,這與試驗結果存在一定誤差.產生這一誤差主要原因,可能在于剝離過程中剝離面之間的摩擦和機械咬合作用.在荷載作用下,砌體與纖維粘結區域會發生開裂,當裂縫尖端附近區域的結合面剪應力達到極限時,纖維材料與砌體間出現剝離[3].在這個區域,纖維材料和砌體結構之間存在部分粘結,隨著裂縫擴展,當粘結面僅存在摩擦力時徹底剝離[4].所以,纖維材料從砌體結構粘結基體里拔出一般要經歷三個過程[5]:加載前,纖維材料與砌體粘結的部分區域內存在一些裂縫和空隙;加載后,原本存在的裂縫和空隙會和加載時新出現的裂縫貫通起來,形成一個裂縫發展區域而逐漸向試件內部延伸,在裂縫區域產生以后,剪應力因裂縫面的機械咬合作用減小相對緩慢[6].在這個區域內,靠近加載端的部分最先剝離,剝離過程中僅存在機械咬合作用[7-8].在外荷載持續作用下,剝離區域不斷向粘結界面深處發展,直至擴展于整個粘結面,從而使纖維材料與基體整體脫離.
為考慮剝離過程中的摩擦和機械咬合作用,本文在Yuan和Teng雙線性模型的基礎上,提出了三線性模型,表達了纖維材料剝離過程中粘結滑移關系.基于斷裂力學,對纖維受力至剝離過程進行了推導,得到了不同階段下的纖維材料粘結應力以及荷載、滑移表達式,完成了荷載滑移關系曲線,與實驗吻合良好.
1 控制方程
圖1為纖維材料與砌體結構粘結受力圖,從圖中可知聚合物纖維網面層粘結砌體受拉時的形態.假定纖維材料在粘結層受均勻分布的軸向應力,忽略彎曲作用;假定粘結層僅受切應力,可以得到以下方程:
(1)
σptpbp+σctcbc=0
(2)
其中,τ為粘結層的切應力,σp為纖維材料的軸向應力,σc為砌體基體的軸向應力.
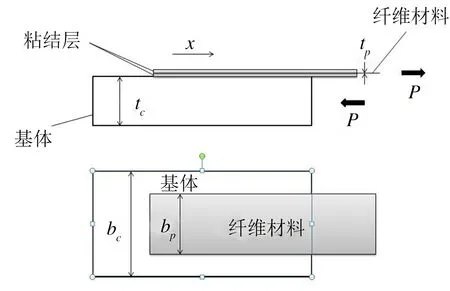
圖1 纖維材料與砌體結構粘結受力圖
粘結層、纖維材料與基體的本構方程可表示為:
τ=f(δ)
(3)
(4)
(5)
δ定義為兩粘結端的相對位移量,即
δ=up-uc
(6)
將方程(2)~(6)代入式(1),引入斷裂能Gf參數得到式(7) 、式(8):
(7)
(8)
其中,
(9)
式(7)為圖1所示的粘結節點的控制微分方程,定義以f(δ)表示的界面切應力與剪切滑移進行求解.斷裂能Gf即為粘結滑移曲線下的面積.
2 粘結滑移模型
本文提出的模型如圖2所示,基于Yuan和Teng雙線性模型,考慮了纖維材料與基體剝離面的摩擦和機械咬合作用,當粘結應力下降至剝離最后階段時存在一個平穩的剝離過程,最后達到極限滑移后完全剝離.根據模型,粘結切應力隨界面滑移量線性增加,直至達到滑移量的最大應力τf時所對應的滑移為δ1.界面軟化開始時,切應力隨界面滑移線性減小.當滑移超過(1-A)δ2+Aδ1時,此時處于即將剝離的臨界區域,因纖維材料與基體之間的機械咬合作用,切應力趨近于Aτf.當滑移超過δf時,切應力為0,表明粘結發生剪切破壞,宏觀表現為界面剝離.界面剝離后沒有任何殘余抗剪強度.
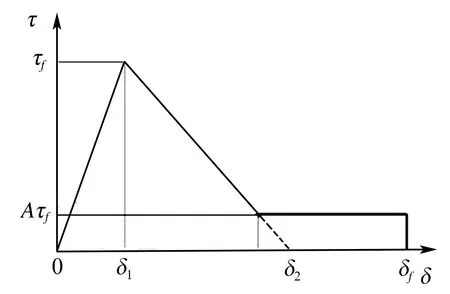
圖2 粘結滑移模型
圖2所示的粘結滑移模型的數學表達式如下:
(10)
3 剝離階段分析
根據上述粘結滑移模型,可通過控制方程求解,得到粘結界面切應力分布以及節點的荷載-位移關系,圖3為界面切應力分布.下面將逐步給出求解方法并給出相應的荷載-位移關系.


圖3 纖維剝離過程各階段切應力分布
3.1 彈性階段
在初始荷載作用下,纖維材料-基體界面間不存在剝離現象,整個粘結長度下接觸面處于彈性狀態,如圖3(a)所示.將式(10)代入式(7)得到微分方程:
(11)
其中,
(12)
x=0,σp=0
(13)
(14)
根據邊界條件求解式(11)得到滑移、切應力和軸向應力的表達式:
(15)
(16)
(17)
當達到最大滑移時,x=L,可以得到荷載-位移表達關系:
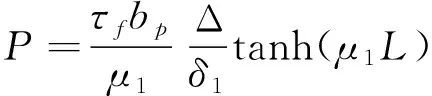
(18)
3.2 彈性軟化階段
當切應力達到τf時,剝離開始,粘結界面的一部分進入軟化狀態,其余仍處于彈性狀態,如圖3(b)所示.荷載隨著剝離長度a遞增.將式(10)代入(7)得到微分方程:
(19)
(20)
其中
(21)
x=0,σp=0;
(22)
x=L-a,δ=δ1,τ=τf
(23)
(24)
(25)
(26)
將x=L-a代入式(26),得
(27)
當δ1≤δ<(1-A)δ2+Aδ1,L-a≤x≤L時
(28)
(29)
(30)
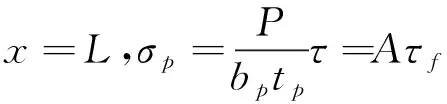
(31)
(32)
(33)
-A(δ2-δ1)cos(μ2a)=δ1-δ2cos2(μ2a)
(34)

(35)
將式(31)代入式(30)
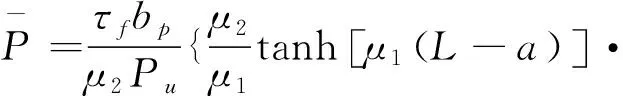
cos(μ2a)+sin(μ2a)}
(36)
(37)
當式(36)導數為0時可得到最大Pu,此時對應的L為此階段的有效粘結長度:
(38)
(39)
對于具有無限粘結長度的點而言,其粘結力至少為所施加荷載的97%.基于這個定義得到:
(40)
3.3 臨界剝離階段
當切應力下降到Aτf時,因纖維材料和基體之間僅存摩擦和機械咬合作用,切應力趨近于平穩,粘結界面處于臨近剝離狀態,如圖3(c)所示.處于平穩點X=L-d時粘結界面應力及荷載為:
(41)
(42)
式(42)對d求導得:
(43)
有效粘結長度為:
(44)

(45)
根據Yuan和Teng的試驗數據,第二個階段得到的粘結長度為28.1 mm,第三階段為137.6 mm,兩個階段對應的荷載分別為5.8和6.6 kN.結果表明超過第二階段后,隨著粘結長度的增加所影響的荷載結果相對較小.所以有效粘結長度的計算取第二階段的結果較為合理.
3.4 粘結破壞階段
在此階段,表現為纖維材料逐漸脫離基體,并沿粘結面傳播.在開始脫離時,δ增至δf,可表達為:
(46)
(47)
隨著剝離過程的進行,切應力從減小到趨于平緩.界面的粘結狀態包括三種狀態,分別是彈性狀態、軟化狀態和剝離狀態.假設從纖維材料的加載端開始的剝離長度為h,方程(24)~(26),(28)~(30)仍然有效,所以位移關系為:
(48)
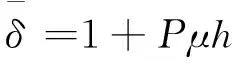
(49)
4 理論值與試驗值對比
依據本文公式,計算纖維材料與砌體拉拔過程中的荷載—滑移曲線,并分別與PBO纖維網面層加固燒結磚砌體和FRP加固混凝土粘結滑移試驗曲線對比,如圖4所示.由圖4(a)可知,試驗中PBO纖維網的拉應力—滑移曲線的試驗值與計算值吻合良好,峰值應力誤差為4.3%.從圖4(b)可以看出,在達到最大拉力前,本文計算結果與Yuan和Teng模型的計算結果均與試驗值有良好的一致性.當滑移量達到最大應力對應值后,Yuan和Teng的計算拉力值保持恒定,與試驗值有明顯區別,誤差分別達到7.62%、 11.57%和13.89%.本文計算結果與試驗值吻合良好,誤差僅為2.37%、0.18%和0.45%.由此可見,本文提出的三線性粘結滑移本構模型,考慮了纖維材料在剝離階段與基體間的摩擦和機械咬合作用,能較好地反映試驗中的粘結滑移狀態,與試驗值吻合良好.
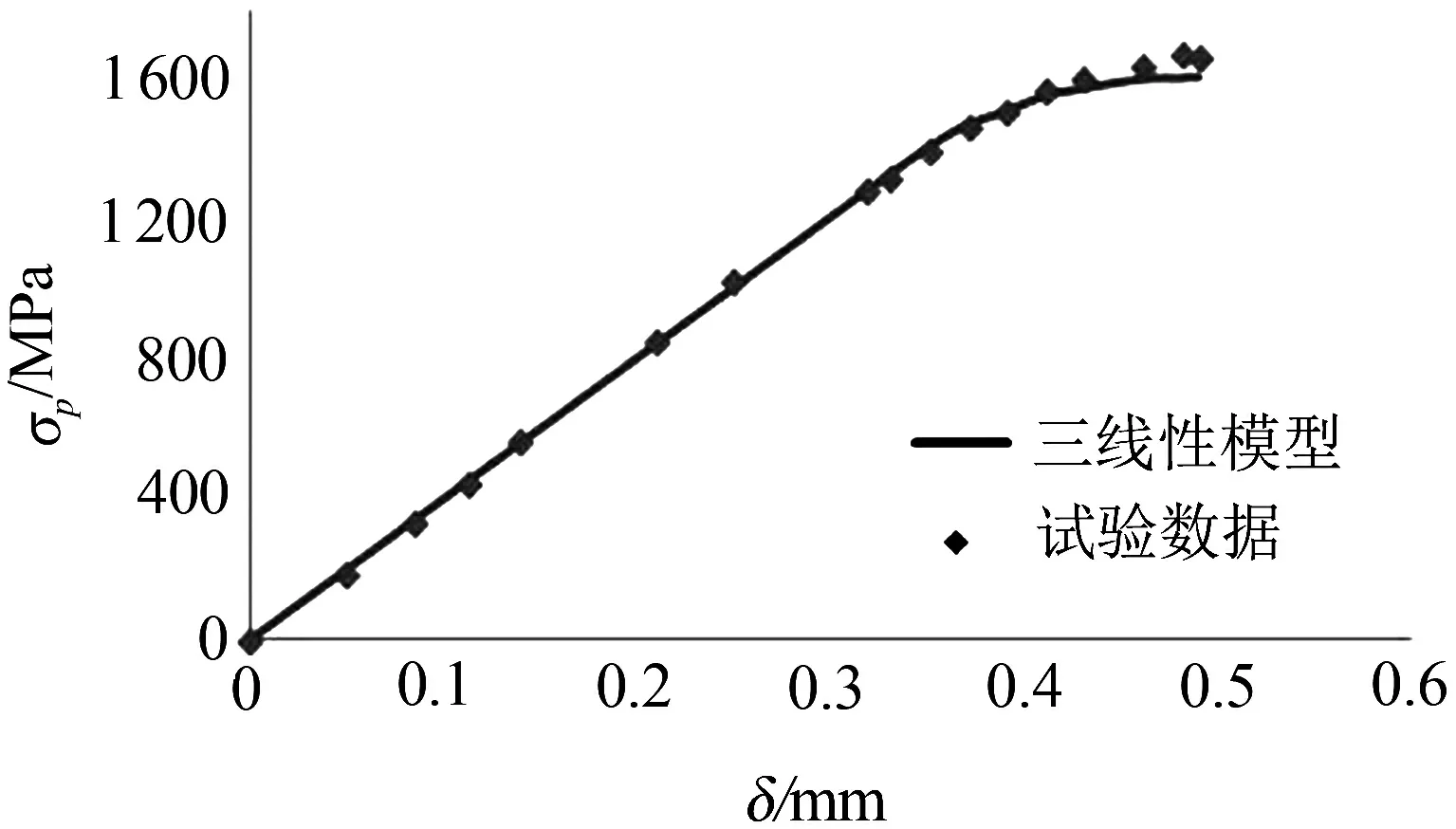
(a) PBO纖維網面層加固砌體
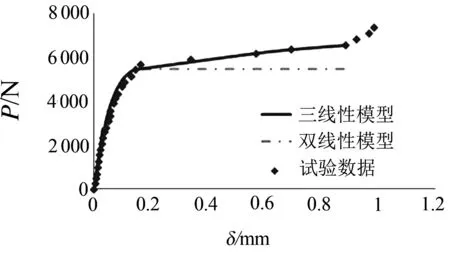
(b) FRP加固混凝土圖4 粘結滑移試驗曲線
5 結論
本文分析了聚合物纖維網面層加固砌體剝離過程的粘結應力分布規律,考慮纖維材料與基體間的摩擦和機械咬合作用,在雙線性模型的基礎上提出了三線性粘結滑移模型,在求解過程中,基于斷裂力學采用了符合實際的三線性粘結滑移模型,推導出不同加載階段界面剪應力分布和荷載位移的關系的表達式,理論計算結果與試驗結果吻合良好.但基于試驗數據限制,本模型未考慮纖維網的網格尺寸等參數對摩擦和機械咬合作用的影響,這有待進一步研究.

