液體火箭發動機雷列槽結構參數對密封動態穩定性的影響

楊文靜 沈文金 葉小強 金志磊

(北京航天動力研究所 北京 100076)

由于液膜潤滑非接觸式機械密封運轉時避免了密封端面之間直接的固體摩擦磨損，使用壽命顯著提高，因而在液體火箭發動機渦輪泵中獲得了廣泛應用[1-2]。近年來，國內外眾多學者對渦輪泵密封開展了系列研究，但多限于穩態特性，而對液膜密封動態特性的研究則多基于空化效應或端面形貌等因素。張國淵等[3]以內外雙螺旋槽中間密封壩結構的端面密封為例，分析了轉速、壓差和槽深等對密封特性參數的影響。陳國忠[4]提出了一種動靜結合型機械密封以解決渦輪泵密封中的兩相流問題。雷晨輝[5]對雷列槽密封進行了流固熱耦合計算，并對結構參數進行了優化。馮瑞鵬[6]討論了渦輪泵用雙螺旋密封端面流體膜汽化相變特性和密封性能。LIU等[7]分析了擾動對波度密封動態性能的影響。ZHAO等[8]對比了不同轉速和壓力下空化模型對動態剛度和阻尼系數的影響。楊文靜等[9]分析了錐度和波度對液膜密封動態特性的影響。孟祥鎧等[10]研究了考慮空化效應時不同結構參數對螺旋槽液膜密封動力學特性的影響。孫鑫暉等[11]在計入空化效應的基礎上，分析了液膜密封熱流體動態特性。然而，雷列槽液膜密封作為液體火箭發動機渦輪泵用密封的典型代表，鮮見關于其動態特性和密封穩定性影響因素的研究報道。

本文作者以雷列槽端面密封為研究對象，采用有限元法和小擾動法求解穩、動態雷諾方程，探究雷列槽結構參數對動態特性系數和密封穩定性的影響，為液體火箭發動機渦輪泵密封的理論設計及結構優化提供參考。

1 計算模型

1.1 幾何模型

圖1為雷列槽密封動環端面及摩擦副結構示意圖。

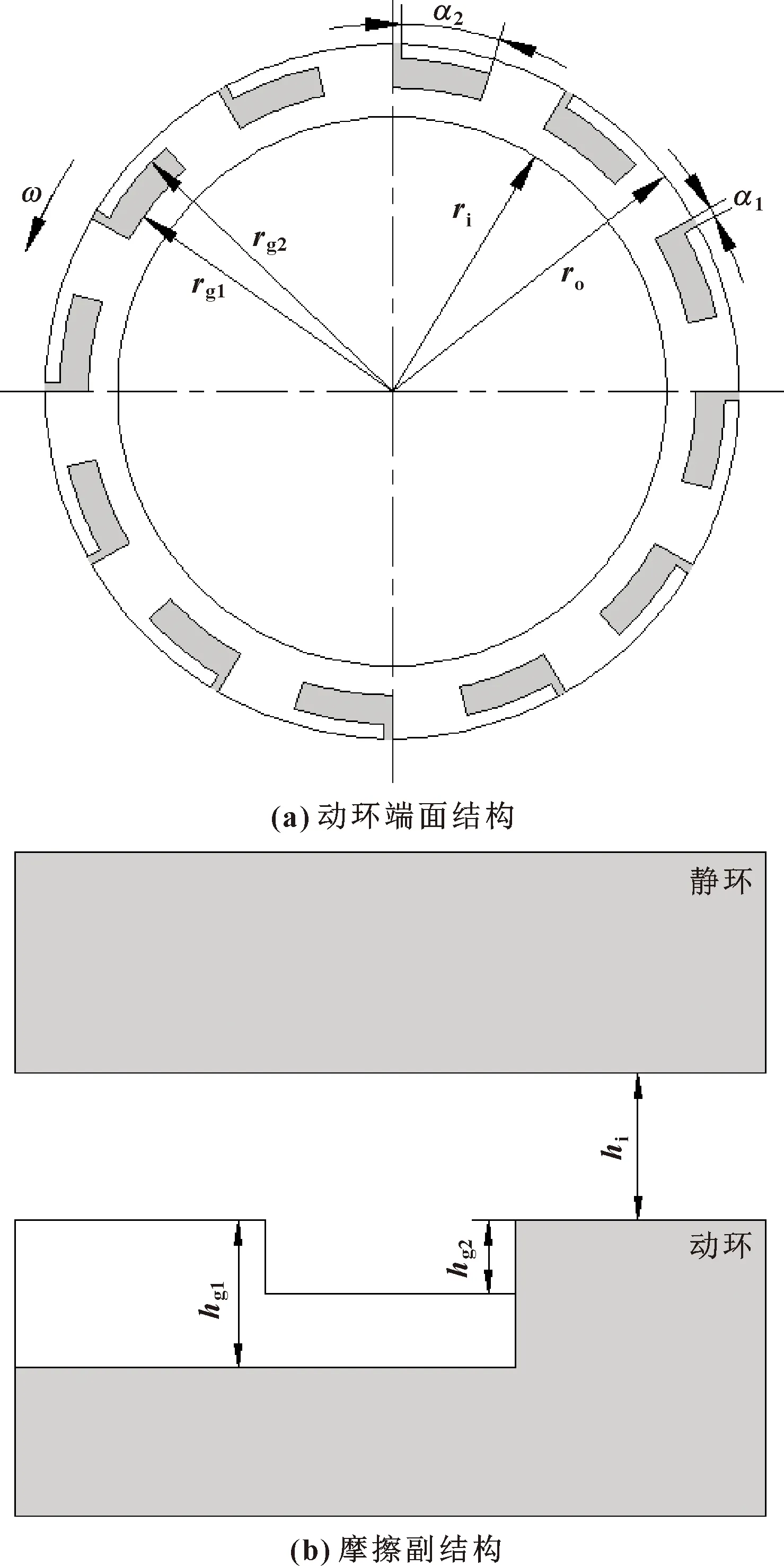
圖1 雷列槽密封動環端面和摩擦副結構示意

雷列槽分為深槽區和淺槽區兩部分，α1和hg1分別為深槽槽寬和槽深，α2和hg2分別為淺槽槽寬和槽深，rg1為淺槽內徑，rg2為淺槽外徑，ri為密封端面內徑，ro為密封端面外徑，hi為非槽區平衡膜厚，ω為動環轉速。計算時所采用的雷列槽結構參數與操作參數詳見表1。

表1 雷列槽密封結構參數與操作參數

1.2 數學模型

由于雷列槽深槽區部分的引流作用，液膜流經該區域時的壓降能得到有效緩解，因此密封端面較難發生空化，假設端面介質為層流流動且黏度、溫度保持不變的牛頓流體，由N-S方程和連續性方程可得包含液膜離心慣性項的雷諾方程[12]如下：

(1)

式中:r、θ、h、p分別為端面任一處的半徑、角度、膜厚和壓力;ρ、μ分別為介質的密度和動力黏度。

2 密封動態剛度和阻尼系數

圖2所示為雷列槽密封動力學模型，假設密封靜環受到3個方向的微擾：沿z軸的軸向移動z、繞x軸的角向擺動α和繞y軸的角向擺動β，并且z=Δzeiυt，α=Δαeiυt，β=Δβeiυt，則密封端面液膜厚度和液膜壓力[13]可表示為

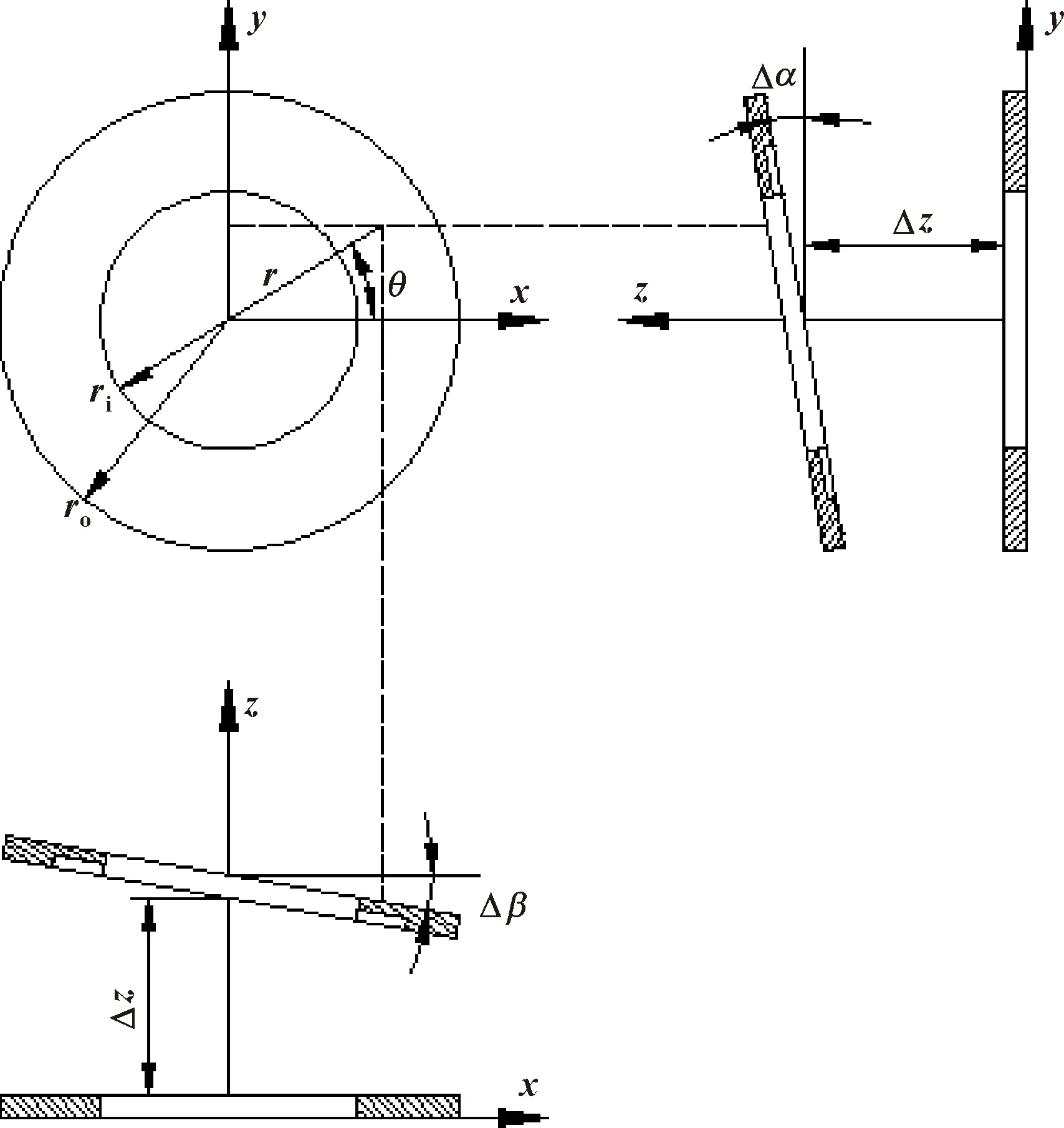
圖2 密封環擾動模型

h=h0+Δzeiυt+rsinθΔαeiυt-rcosθΔβeiυt

(2)

p=p0+pzΔzeiυt+pαΔαeiυt+pβΔβeiυt

(3)

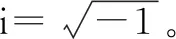
將式(2)和式(3)代入式(1)，只保留到微擾的一次方項，由于定義的微擾量為復數，所以pz、pα和pβ也都是復變量，令pz=pzr+ipzi，pα=pαr+ipαi，pβ=pβr+ipβi，得：

(4)

(5a)

(5b)

(6a)

(6b)

(7a)

(7b)

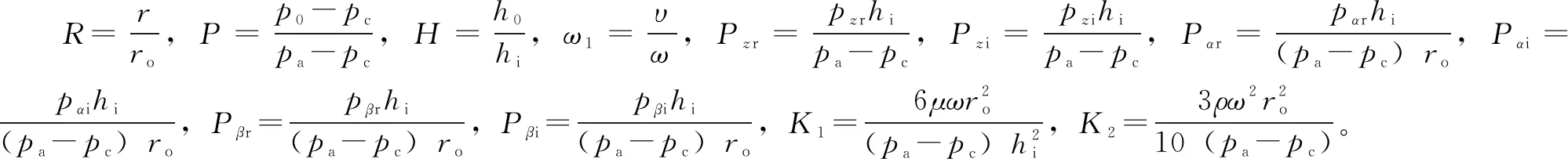
在文中后續計算中，如無特殊說明，ω1=1。

上述方程滿足的邊界條件如下：

(1)強制性邊界條件

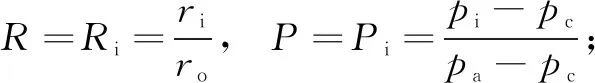
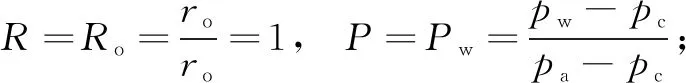
內外徑處：Pz=Pα=Pβ=0。

(2)周期性邊界條件

P(θ,R)=P(θ+2π,R)；

Pn(θ,R)=Pn(θ+2π,R)，n=z，α，β。

當Pz、Pα和Pβ求得后，密封量綱一化動態剛度和阻尼系數可按下式計算：

(8)

(9)

則有量綱液膜動態特性系數為

(10)

式中：j，g=x，y。

3 密封穩定性

經計算得知，kzx、kzy、kxz、kyz和czx、czy、cxz、cyz、cxy、cyx與其他動態剛度和阻尼系數相比數值很小，可設為0；角向剛度系數kxx=kyy，角向耦合剛度系數kxy=-kyx，角向阻尼系數cxx=cyy，因此密封靜環三自由度的微擾運動可簡化為一個沿軸向的移動和另一個沿2個正交軸的角向擺動。考慮靜環撓性安裝時的彈簧剛度和密封阻尼，得到靜環的微擾運動方程為

(11)

(12)

式中:m為靜環質量;I為靜環轉動慣量;ks為彈簧剛度;cs為密封阻尼;ksx、ksy為彈簧角向剛度;csx、csy為密封角向阻尼。

3.1 軸向微擾穩定性

式(11)為二階常系數線性齊次微分方程，設微擾運動的解為z=zεest，將其代入式(11)得微擾運動的特征方程為

ms2+(czz+cs)s+kzz+ks=0

(13)

由此得到特征根為

通過對方程特征根的討論可以對密封軸向穩定性作出分析。

3.2 角向微擾穩定性

同理，設式(12)的解為α=αεest，β=βεest，將二者代入式(12)得角向微擾運動的特征方程為

a0s4+a1s3+a2s2+a3s+a4=0

(14)

式中：a0=I2；a1=I(cyy+csy+cxx+csx)；a2=I(kyy+ksy+kxx+ksx)+(cxx+csx)(cyy+csy)-cyxcxy；a3=(cxx+csx)(kyy+ksy)+(kxx+ksx)(cyy+csy)-cyxkxy-kyxcxy；a4=(kxx+ksx)(kyy+ksy)-kyxkxy。

保證系統平衡穩定性的前提是式(14)全部特征根的實部均為負值[15]，考慮臨界失穩狀態(實部為0)，有s=iυcr，將其代入特征方程式(14)得：

(15)

令式(15)的實部、虛部分別為0可得：

(16)

因此可得雷列槽密封的臨界頻率和臨界轉動慣量：

(17)

(18)

式中：

4 計算結果與分析

4.1 程序驗證

為了驗證文中程序，計算了不同轉速下穩態液膜剛度與低頻率數時(σ=2K1ω1=1)的動態液膜剛度，結果對比如圖3所示。可知，在頻率數較低時，動態液膜剛度與穩態液膜剛度隨轉速的變化趨勢一致，吻合較好，因此可認為文中程序算法是正確的。

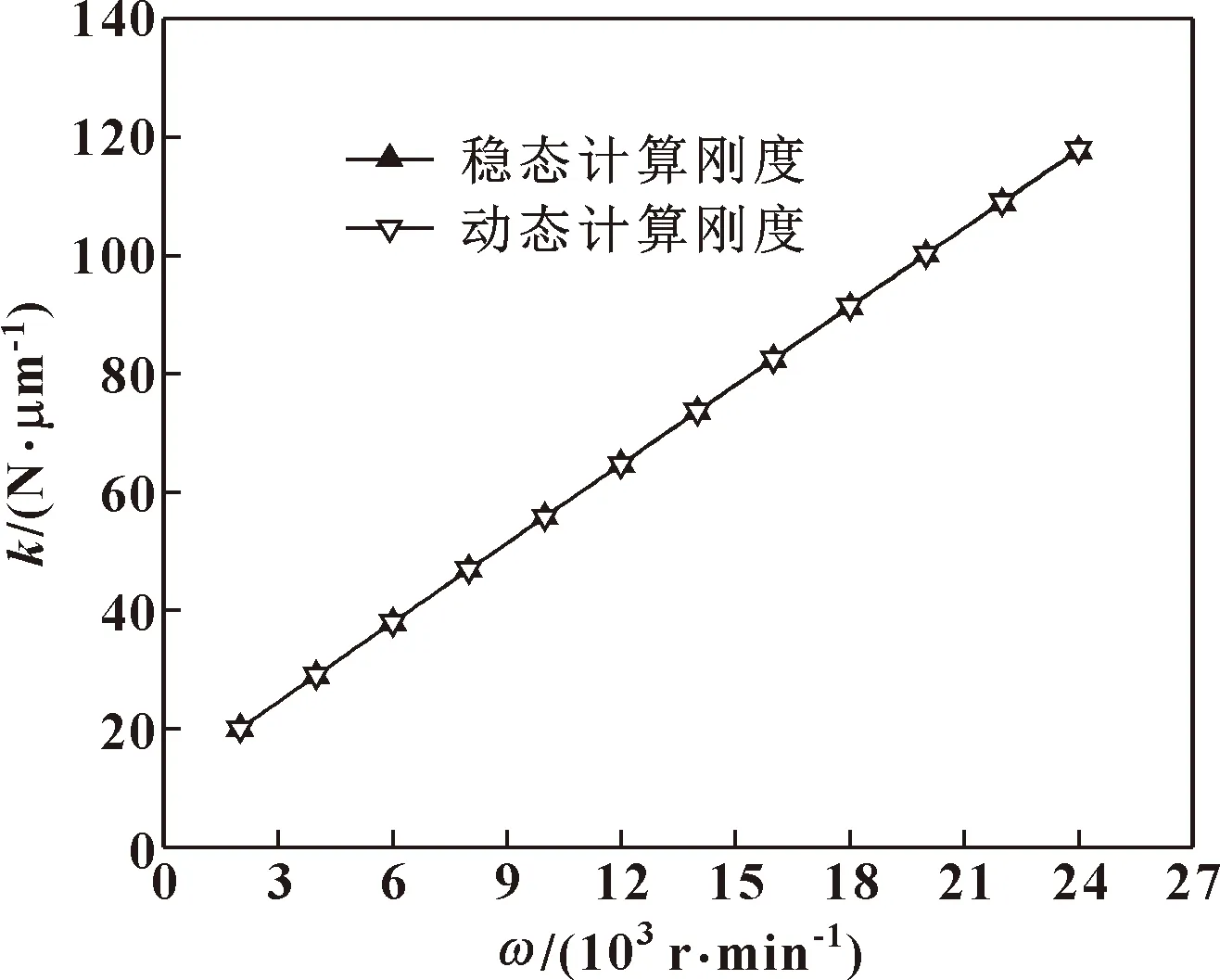
圖3 動態剛度與穩態剛度的對比

4.2 雷列槽結構參數對動態特性系數的影響

槽數對動態特性系數的影響如圖4(a)所示。可知，當槽數由4增加至16時，Kxx和Kzz隨著槽數的變化而變大，但趨勢逐漸變緩。這主要是由于槽數增加，流體動壓效應增強，并且槽數較小時，槽數的變化對流體動壓效應的影響更顯著。但當槽數進一步增大時，相鄰兩槽區之間的臺區減小，淺槽槽根處高壓區受下一周期深槽區壓力的影響增強，因而當槽數由16增加至20時，Kxx和Kzz隨槽數的變化趨勢逐漸變大。從圖4(a)中還可以看出，Kxy、Cxx和Czz隨著槽數的增加先減小后趨于平穩，這表明，Kxy、Cxx和Czz與流體動壓效應呈負相關關系。由于流體動壓效應變化對動態特性系數的影響機制類似，為避免重復，下文中將不再贅述。

淺槽內徑對動態特性系數的影響如圖4(b)所示。可知，Kxx和Kzz隨著淺槽內徑的增加而減小，且下降趨勢逐漸變緩，而Kxy、Cxx和Czz隨著淺槽內徑的增加而增加，且上升趨勢逐漸變大。相比較而言，淺槽內徑對Kxy的影響比對Kxx和Kzz的影響更加顯著，Czz隨淺槽內徑的變化程度比Cxx更加明顯。

淺槽槽寬對動態特性系數的影響如圖4(c)所示。可知，Kxx和Kzz隨著淺槽槽寬的增加而增加，且上升趨勢逐漸變大，Kxy、Cxx和Czz隨著淺槽槽寬的增加而減小，且下降趨勢逐漸變緩。從圖4(c)中還可以看出，淺槽槽寬的變化對Kzz和Czz的影響明顯大于其余動態剛度和阻尼系數。

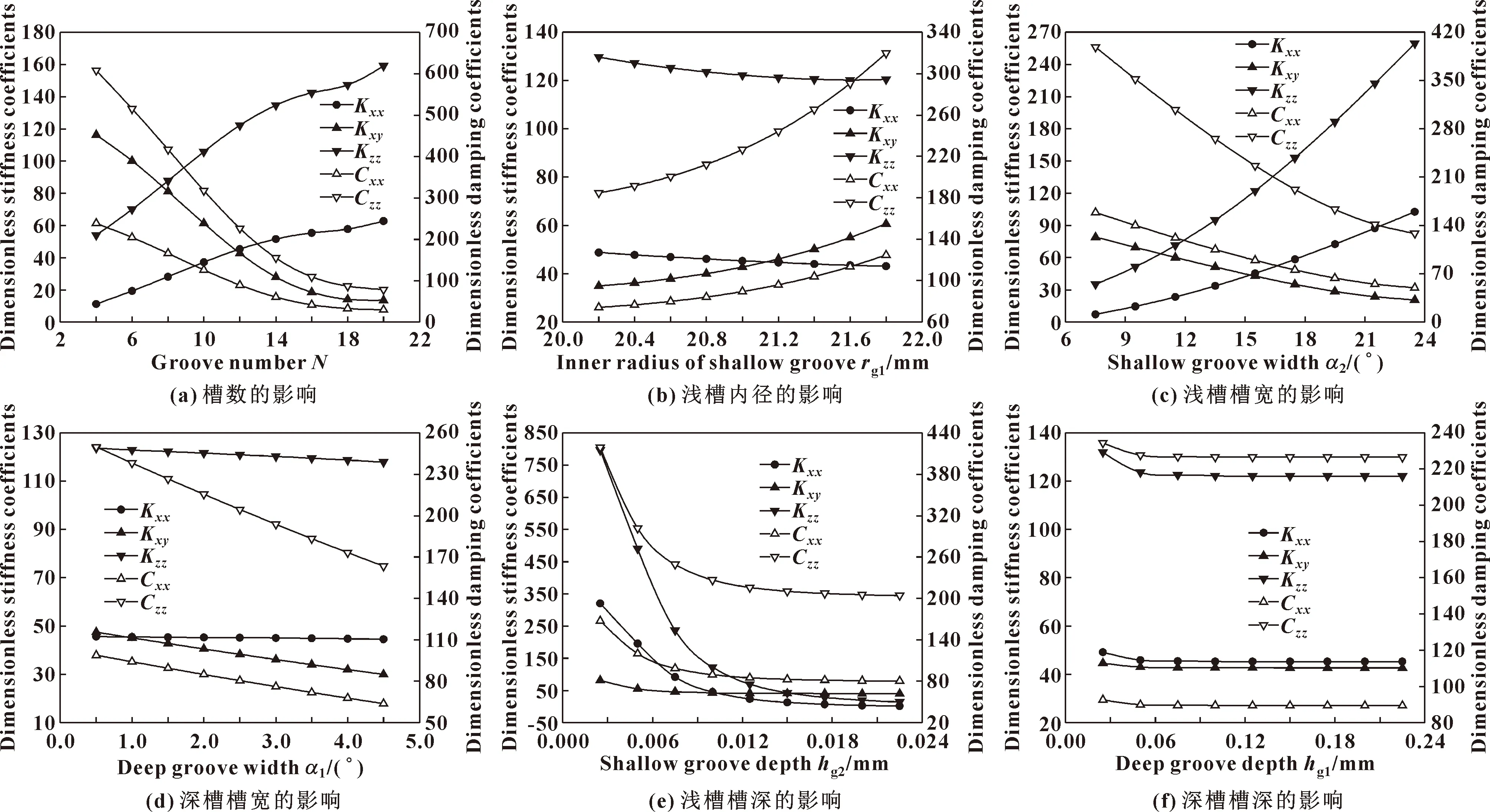
圖4 雷列槽結構參數對動態特性系數的影響

深槽槽寬對動態特性系數的影響如圖4(d)所示。可知，動態剛度系數Kxx、Kzz、Kxy和動態阻尼系數Cxx、Czz均隨著深槽槽寬的增加而減小，這表明，動態特性系數與流體靜壓效應呈負相關關系。動態剛度系數中，Kxy受深槽槽寬的影響最大，Kzz次之，Kxx受深槽槽寬的影響最小，呈幾乎不變的趨勢;動態阻尼系數中，Czz隨深槽槽寬的變化程度明顯大于Cxx。

淺槽槽深對動態特性系數的影響如圖4(e)所示。可知，動態剛度系數Kxx、Kzz、Kxy和動態阻尼系數Cxx、Czz均隨著淺槽槽深的增加呈現先減小后趨于平穩的趨勢，這是由于淺槽槽深增加，流體靜壓效應增強。動態剛度系數中，Kzz受淺槽槽深的影響最大，Kxx次之，Kxy受淺槽槽深的影響最小;動態阻尼系數中，淺槽槽深對Czz的影響比對Cxx的影響更加顯著。

深槽槽深對動態特性系數的影響如圖4(f)所示。可知，當深槽槽深由0.025 mm增加至0.05 mm時，動態剛度系數Kxx、Kzz、Kxy和動態阻尼系數Cxx、Czz均呈逐漸減小的趨勢;當深槽槽深hg1≥0.05 mm時，各個動態特性系數基本不變。這是因為深槽槽深較小時，隨槽深增加，流體靜壓效應增強；但當槽深增加到一定程度時，其對流體靜壓效應的提升幾乎無影響。

4.3 密封穩定性分析

4.3.1 軸向穩定性分析

對由式(13)所得到的特征根進行討論，具體如下：

(1)當(czz+cs)2≥4m(kzz+ks)時，特征方程有2個相異或相等實根。由上述分析可知，不同結構參數下密封軸向剛度和阻尼系數kzz、czz均為正，又由于彈簧剛度ks和密封阻尼cs為正，所以有s<0。即密封靜環的運動為衰減的非往復運動，雷列槽密封不會發生軸向失穩。

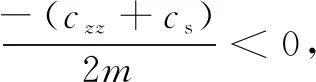
4.3.2 角向穩定性分析

雷列槽結構參數對臨界頻率比(臨界頻率與轉速的比值)和臨界轉動慣量的影響如圖5所示。

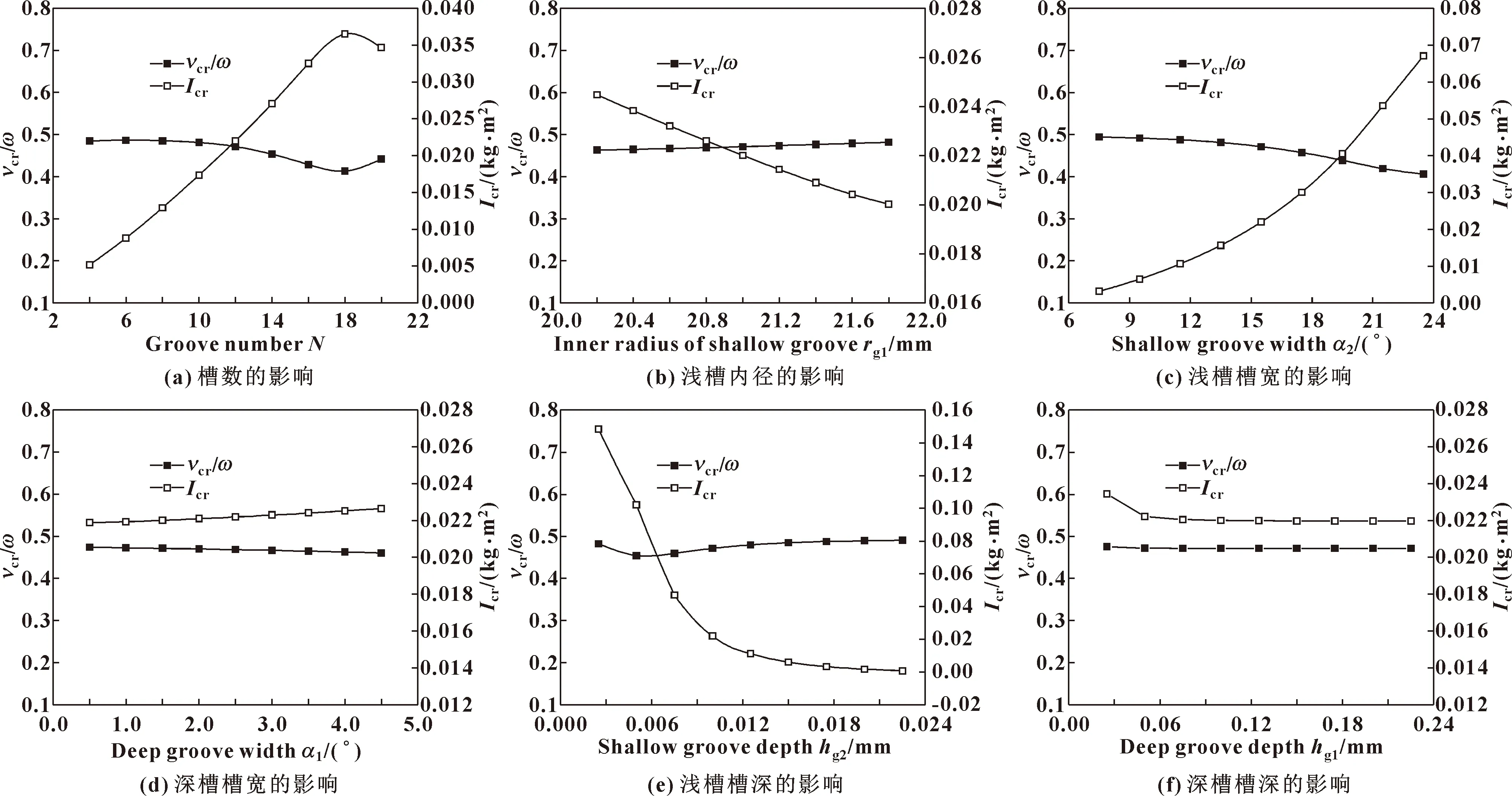
圖5 雷列槽結構參數對角向穩定性的影響

由圖5可知，隨著各個結構參數的變化，臨界頻率比雖小有波動，但基本均處在0.4～0.5之間。這表明，在液體火箭發動機雷列槽端面密封中，存在“半頻擺動”現象，該現象與軸承中存在的“半速渦動”特性相類似，是液膜密封的一種固有特性，并且表現為小于0.5。由式(18)可知，臨界轉動慣量的變化反映了角向動態特性系數綜合作用的結果，具體表現為，臨界轉動慣量隨著槽數的增加先增大后減小，在槽數為18時達到最大；淺槽內徑增加，臨界轉動慣量減小；淺槽槽寬增加，臨界轉動慣量有所增大，且上升趨勢逐漸變大，而深槽槽寬增加，臨界轉動慣量變化不明顯，只是稍有變大；淺槽槽深增加，臨界轉動慣量呈先下降后趨于平穩的趨勢；當深槽槽深由0.025 mm增加至0.05 mm時，臨界轉動慣量稍有下降，深槽槽深進一步增加，臨界轉動慣量基本保持不變。綜上分析可知，槽數或淺槽槽寬的減小、淺槽槽深的增加均會導致過小的臨界轉動慣量，進而容易引起雷列槽密封角向失穩。

5 結論

(1)采用有限元法和小擾動法求解包含液膜離心慣性項的穩、動態Reynolds控制方程，獲得了密封動態剛度和阻尼系數，并對密封軸向和角向穩定性進行了分析，為雷列槽密封的動態穩定性設計提供指導。

(2)同一雷列槽結構參數的變化對動態剛度和阻尼系數的影響程度不同；槽數、淺槽槽寬增加，淺槽內徑減小時，軸向剛度系數和角向剛度系數變大，角向耦合剛度系數和動態阻尼系數變小；深槽槽寬、淺槽槽深增加，動態剛度和阻尼系數均減小；深槽槽深的變化對動態剛度和阻尼系數影響較小。

(3)雷列槽密封不會發生軸向失穩，角向存在“半頻擺動”現象，并且臨界頻率比小于0.5；槽數、淺槽槽寬減小，淺槽槽深增加時，雷列槽密封容易發生角向失穩。