脈動熱管溫度時間序列的關聯維分析
周屹 楊洪海 張苗
東華大學環境科學與工程學院
脈動熱管(Pulsating Heat Pipe,PHP)是一種新型的高效換熱元件,具有傳熱效率高,結構簡單[1]等優點。目前國內外對PHP已有廣泛的研究。脈動熱管雖然結構簡單,但其內部的傳熱過程復雜,實驗方面,主要是從工質,充液率,傾斜角[2]等方面進行研究。理論方面,C heng和 Ma[3]通過匯總理想狀態氣體方程和熱力學第一定律,得到了液塞和氣塞的質量 -彈簧-阻尼模型。理論模型對管內工質的狀態和運行都進行了一定的簡化,無法真實的反應管內流體的運動狀態,對于這種系統可以采用非線性理論進行研究。宋延熙[4]等通過關聯維,H urst 指數等非線性分析方法表明,脈動熱管內的溫度波動是確定性混沌運動。Q u[5]等使用李雅普諾夫維數等一系列判別混沌方法,表明脈動熱管的弱混沌特性。方海洲[6-7]等運用功率譜,H urst指數,小波分解等非線性分析方法,發現溫度信號波動屬于分形下的混沌行為。以上對溫度時間序列的分析,均測量的是管壁溫度。雖然銅管的導熱系數高,但導熱的延遲不可忽視,因此,本文搭建脈動熱管可視化試驗臺,并測量管內的流體溫度進行關聯維分析。
1 實驗系統
本實驗的實驗系統由脈動熱管,電加熱系統,冷卻系統和溫度采集系統等組成。實驗裝置圖則由圖 1所示。

圖1 實驗裝置圖
脈動熱管采用石英耐熱玻璃彎折而成,內徑2.5 mm,外徑 4 mm,總高度 240 mm,其中蒸發段70 mm,冷凝段150 mm,絕熱段20 mm。蒸發段均勻的纏繞電熱絲,通過直流電源(MP1203D)進行加熱,冷凝段置于風管中進行強制冷卻。為了減少散熱,將蒸發段整體置于一方盒子中,四周縫隙用密封膠進行密封,除此之外,在方盒子的內壁面采用鋁箔反射膜-珍珠棉(6 mm)-鋁箔反射膜的三層保溫結構。總計使用了6個K型熱電偶,測量精度為±0 .1 ℃,1號和2號測量蒸發段管內流體溫度,3 號和 4 號測量冷凝段管內流體溫度,5號在保溫層內側,6號在保溫層外側。
在實驗前為了充液以及排除管內的不凝性氣體,需要對脈動熱管進行抽真空處理,當真空度達到 1.5× 10-3Pa時,保壓15分鐘后進行充液,充液率為55%。溫度由Aglient 34972A進行采集,掃描頻率為20 Hz。
詳細實驗工況見表1。

表1 實驗工況
2 關聯維方法
2.1 關聯維
分形理論是描述混沌信號的一種手段,分形是沒有特征長度但具有一定意義的自相似圖形的總稱,最初由 Mandelbrot 在研究海岸線等不規則曲線時提出,之后人們發現自然界普遍存在分形現象。分形的主要特征是自相似性,即局部與整體存在某種相似性,混沌的奇怪吸引子具有不同于通常幾何形狀的無限層次的自相似結構,這種幾何結構可以用分形維數來描述[8-9]。現已有許多分形維數的定義和計算方法,本文使用關聯維數D2計算分形維數。
1983 年,G rassberger 和 Procaccia[10]提出了一種估算D2的經典算法,其算法一般簡稱為 GP算法。具體步驟如下:
1)估計時間序列x(i)i=1,2,……,N的時間延遲τ和嵌入維數m,等到重構相空間X(i)
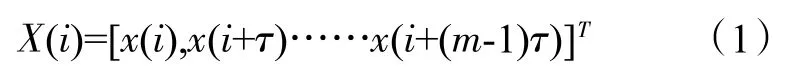
式中:i=1,2,……,M,M=N-(m-1)τ。
2)計算關聯積分

式中:θ(x)是Heaviside單位函數。
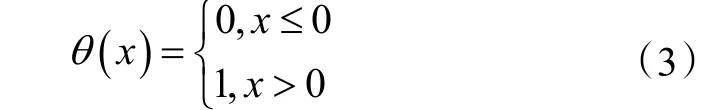
||X(i)-X(j)|| 定義了矢量X(i)與矢量X(j)之間的距離。
3)在r的無標度區域內,雙對數曲線ln(r)~ln(C(r))滿足線性關系,線性區域的斜率即為D2。

2.2 參數選取
在使用G-P算法計算關聯維時,嵌入維數m和延遲時間τ的參數選取極為重要。延遲時間過小,信息不容易顯示。延遲時間過大,則坐標值x(n)和x(n+τ)相互之前的動力學聯系不能展現。有很多種方法可以確定延遲時間,自相關函數法和互信息法[11]是常用的兩種方式。
Lorenz系統由Lorenz于 1963年提出,由如下常微分方程組描述:
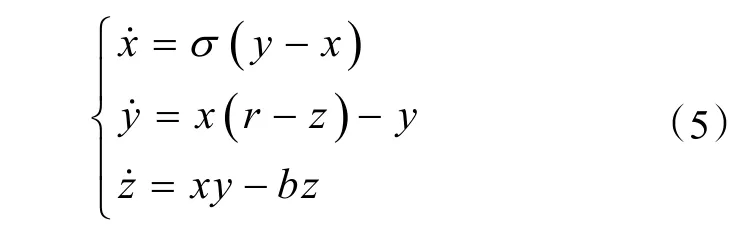
式中:x,y,z均為時間t的函數,參數σ=10,r=28,b=8/3初值取[x,y,z]=[0,1,0],積分步長為0.01。
取 Lorenz 吸引子x分量的前 5000 個點為例,進行計算。圖 2為計算結果。

圖2 Lorenz吸引子x分量的自相關函數和互信息
取自相關函數下降到初始值的 1-1/e 或互信息的第一個極小值點作為最優延遲時間,根據計算數據,Lorenz吸引子x分量的延遲時間取12。
嵌入維數m采用飽和關聯維方法[12]來確定,即逐步增加嵌入維數,直到無標度區域的斜率維持在一個常數時,將此時的m作為嵌入維數。
2.3 Lorenz吸引子x分量的關聯維
圖3是Lorenz吸引子x分量的雙對數曲線,嵌入維數m取1~10。從圖4可以看出,在m≥6之后,此時的斜率不再變化,曲線收斂,關聯維D2基本穩定在2.1左右,標準值D2為2.06[11]。

圖3 Lorenz吸引子x分量的雙對數曲線
3 結果與討論
3.1 溫度時間序列分析
本實驗的脈動熱管由玻璃制作,可以直接觀察到管內的工質流動情況。隨著加熱功率的提升,脈動熱管可以大致分成三種運動狀態。一種是在低加熱功率時,管內液塞幾乎不運行。二種是在中等加熱功率時,管內流體小幅震蕩,但僅限在同一根管的蒸發段和冷凝段之間運行,并不會越過彎頭進入相鄰管。三種是在高加熱功率時,管內工質形成整體的循環流動。基于三種運動狀態,可以對應的將加熱功率大致分為10 W 為低加熱功率,20~30 W 為中等加熱功率,40~ 60 W為高加熱功率。
圖5是丙酮作為工質運行時的溫度時間序列圖,可以看出不同運動狀態對應的溫度時間序列的特征。低加熱功率時,溫度會較長時間的穩定在某一溫度,即管內工質不流動。高加熱功率時,溫度波動的具有一定規律性,頻率較高,也可以說明管內工質在高加熱功率是運行速度較快。
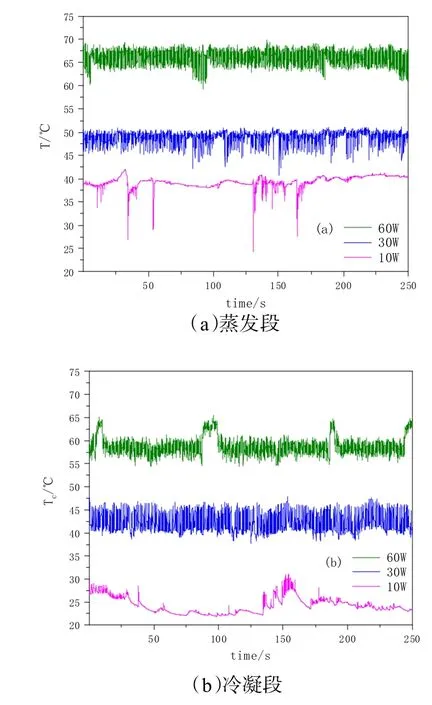
圖5 丙酮溫度時間序列圖
圖6是乙醇作為工質運行時的溫度時間序列圖,首先可以發現上文對運動狀態的分類也適用于乙醇脈動熱管。除此之外,從圖中可以看出丙酮整體的運行情況比乙醇好,原因在于:一是,當加熱功率為60 W時,兩種工質的冷凝段溫度都在60 ℃左右,但丙酮的蒸發溫度更低,說明在同等冷卻方式下,丙酮帶走了更多的熱量,熱阻更低。二是,當加熱功率為30 W時,丙酮和乙醇都不處于整體運動狀態,但丙酮溫度波動頻率高于乙醇,說明在中等加熱功率是,丙酮在單管內的換熱強于乙醇。三是,當加熱功率為 10 W時,乙醇和丙酮均未啟動,可以觀察到丙酮出現非周期性的溫度波動,原因在于雖然加熱功率小無法產生足夠的壓差使液塞運動,但經過一段時間的熱量積累,液塞會被沖到冷凝段,冷凝段低溫的液體運動到蒸發段。這種運動并不能持續進行,這也是溫度序列中間歇性波動的原因。

圖6 乙醇溫度時間序列圖
3.2 加熱功率對關聯維的影響
圖7為丙酮為工質,熱端和冷端在不同加熱功率下關聯維隨嵌入維數的變化趨勢。從圖中可以看出,隨著嵌入維數的增加,關聯維數也不斷增加,并趨于飽和,圖中虛線表示關聯維的飽和值。在不同加熱功率下,飽和關聯維值明顯不同,存在明顯的分界。10 W時溫度序列比較平穩,關聯維較小,隨著加熱功率的增大,溫度序列的波動更加劇烈,非線性程度也發生了變化,60 W時,關聯維達到最大,這表明 PHP 系統的復雜性也在隨加熱功率增加。此外,發現相同加熱功率下,冷凝段的關聯維均小于蒸發段的關聯維,表明蒸發段溫度波動更加復雜,Q u也發現同樣的趨勢。

圖7 丙酮關聯維D2隨嵌入維數m的變化
圖8為乙醇在不同加熱功率下隨嵌入維數的變化趨勢,可以發現與丙酮類似的結論。除此之外,在 30 W和60 W時,丙酮的關聯維值均小于乙醇的關聯維值,可以表明管內丙酮的運動比乙醇更加劇烈,溫度波動的頻率更高,幅度更小,丙酮的傳熱性能也優于乙醇。

圖8 乙醇關聯維D 2隨嵌入維數m的變化
以丙酮為工質,蒸發段的飽和關聯維為9.545,冷凝段的飽和關聯維為8.902,要大于方海洲[7]的計算結果。以乙醇為工質,蒸發段的飽和關聯維為8.509,冷凝段的飽和關聯維為 7.75,關聯維值也大于 Qu[5]的計算結果。表2是關聯維計算的總結。這是由于測量方式的區別導致的不同,本文直接測量流體溫度,而其他文獻測量的均為管壁溫度,雖然銅管的導熱系數大,但并不能真實反映管內流體的運動情況,這也是本文計算的關聯維數值大于文獻的原因。

表2 關聯維計算總結
3.3 關聯維對傳熱的影響
圖9給出了不同加熱功率下,丙酮脈動熱管蒸發段溫度的關聯維和熱阻曲線。從溫度波動曲線和熱阻圖可知,熱阻與關聯維成反比關系。丙酮脈動熱管在20 W時已經熱阻已經降至0.3,觀察到管內工質在此時已經在快速小幅震蕩,雖未形成循環流動,但傳熱能力相比于10 W已經大大加強了。與此相對應的是關聯維的值也有了較大的躍升,這表明隨著脈動熱管傳熱能力的增強,管內的相變換熱愈發劇烈,氣泡的生成頻率增加,整體的復雜性突升。當處于高加熱功率時,此時脈動熱管內部已經形成循環流動,關聯維和熱阻隨加熱功率的變化幅度變小,關聯維基本維持在 8~9 左右,由關聯維的物理意義可知,此時如要準確表述脈動熱管運動情況,至少需要9個變量,例如工質的表面張力,氣化潛熱,與壁面接觸角,充液率等。

圖9 加熱功率對關聯維和熱阻的影響
4 結論
本文設計了脈動熱管可視化試驗臺,以丙酮和乙醇為工質,采集管內流體溫度進行了非線性分析,結論如下:
1、以丙酮作為工質的脈動熱管運行情況要優于乙醇。
2、關聯維D2隨嵌入維數m的增加而增加,m增大到一定值后,關聯維趨于收斂。
3、蒸發段溫度的關聯維略大于冷凝段溫度的關聯維。
4、相比采集壁溫信號,管內流體的溫度信號更能準確反映管內的運動狀態。
5、熱阻與關聯維成反比關系,如要準確描述循環流動的脈動熱管,至少需要 9個變量。

